也谈函数的单调性
2019-01-16胡凤娟保继光
胡凤娟 保继光
(1.首都师范大学教师教育学院 100048;2.北京师范大学数学科学学院 100875)
函数是数学中的核心内容,而单调性是函数的基本性质,也是高中数学教学的重点.但是,在教学实践中存在着许多模糊认识和错误理解.准确把握好函数单调性的概念教学,是切实关注通性通法的重要方面,更是落实数学学科核心素养的需要.
本文首先讨论了函数单调性的定义,然后给出在指数函数单调性、极值和最值教学中的相关建议.
1 函数单调性的定义
在现行的高中数学教材6个版本(人教A版、人教B版、北师大版、苏教版、湘教版和鄂教版)中,函数单调性的定义大同小异,没有本质区别.追溯高中数学教材各时期的版本,函数单调性的叙述也是如此.据了解根据《普通高中数学课程标准(2017年版)》正在修订的教材中,函数单调性的定义也大同小异.下面是人教A版必修一中单调性的定义[1]:
一般地,设函数y=f(x)的定义域为D:
如果对于定义域D内某个区间I上的任意两个自变量的值x1,x2,当x1 如果对于定义域D内某个区间I上的任意两个自变量的值x1,x2,当x1 如果函数y=f(x)在区间I上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间I叫做y=f(x)的单调区间. 查阅了诸多数学相关书籍,发现《中国大百科全书·数学》《数学辞海》以及《数学分析》的教科书基本上都明确区分了单调与严格单调的定义.下面给出《中国大百科全书·数学》中关于单调函数的描述[2]: 如果对D中任意两数x1,x2,当x1 有一些文献将严格单调增函数(严格单调减函数)称为增函数(减函数)、将增函数(减函数)等同于非减函数(非增函数)[3][4],这里不再展开叙述. 数学百科全书(Encyclopedia of Mathematics)[5]上的相关表述是:A real-valued functionfis said to be increasing over an interval if, over that interval, greater input values produce greater (or possibly equal) output values, that is, ifaandbare two values in the interval witha 综上所述,我们建议函数单调性的定义如下: 设函数y=f(x)的定义域为D,区间I⊆D, (1)如果对于任意的x1,x2∈I,当x1 (2)如果对于任意的x1,x2∈I,当x1 由于定义域的英文是domain, 区间的英文是interval,所以将定义域和区间应该分别简记为D和I. 在这个定义下,可以借助导数给出函数的单调性的充要条件. 设函数y=f(x)在区间I上可导,则 (1)y=f(x)是I上增函数的充要条件是f′(x)≥0,x∈I; (2)y=f(x)是I上减函数的充要条件是f′(x)≤0,x∈I. 判断函数f(x)=x5在实数集R上是增函数. 当然,如果想进一步判断严格单调性,还需要更细致的讨论.事实上,不难证明:设函数y=f(x)在区间I上可导.(1)若在区间I上f′(x)≥0,且仅在有限个点为0,则y=f(x)是区间I上的严格增函数;(2)若在区间I上f′(x)≤0,且仅在有限个点为0,则y=f(x)是区间I上的严格减函数. 这样一来,不仅把单调性问题陈述的更加简明,同时也与大学阶段的函数单调性的定义,以及它的英文表述一致,充分体现数学的整体性. 根据中学教材中现行单调区间的定义,若区间I是函数y=f(x)的单调区间,则区间I的任意一个子区间也是y=f(x)的单调区间,也就是说对于给定的函数单调区间不是唯一确定的!这是定义中的大忌. 在教学和评价中,单调区间常常被默认为是使得函数单调的最大区间.但是,在实践中对区间端点的认识还是不到位.另外,需要注意的是,函数的单调性是整体性质,只能在给定的区间上讨论,不能在某一点讨论.比如,问题“f(x)=x2在x=0是单调上升还是单调下降?”本身就是不科学的! 例如在人教A版教材中有考查函数单调区间的例题,在习题中也有类似的题目,如下[6]: 例1图1.3-4是定义在区间[-5,5]上的函数y=f(x),根据图像说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数? 图1.3-4 解函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5].其中y=f(x)在区间[-5,-2),[1,3)上是减函数,在 [-2,1),[3,5]上是增函数. 实际上,根据现行单调区间的定义,函数y=f(x)的单调区间可以是[-5,-2),[-2,1),[1,3),[3,5],也可以是它们各自的任意子区间;按照默认的最大单调区间的理解,函数y=f(x)的单调区间应该是[-5,-2],[-2,1],[1,3],[3,5].原因是闭区间比相应的半开半闭区间更大. 高考中也经常会考查函数的单调区间.例如2018年天津理科卷第20题:已知函数f(x)=ax,g(x)=logax,其中a>1.第1问是:求函数h(x)=f(x)-xlna的单调区间.该题的答案是:函数h(x)的单调递减区间(-∞,0),单调递增区间为(0,+∞).实际上,根据现行单调区间的定义,函数h(x)的单调递减区间可以是(-∞,0),也可以是(-1,0)或(-2,-1);按照默认的最大单调区间的理解,函数h(x)的单调递减区间应该是(-∞,0],它比(-∞,0)更大.类似地,单调递增区间应该是[0,+∞). 基于上述原因,我们认为,教材中最好不出现单调区间这个概念.如果出现,就应该理解为最大的单调区间.只有这样概念才具有确定性和唯一性. 在指数函数的教学中,一般是通过“看图说话”的方法获得它的单调性.给出具体指数函数(如:y=2x和y=3x)的图像,进而“粗暴地”抽象出指数函数的单调性.一些教材还让学生通过计算机进一步验证指数函数的单调性.这种从特殊到一般的处理方式,非常具体、直观,学生易于理解,但在凸显直观的同时,过多地丧失了数学的严谨性. 如何更好的得到指数函数y=ax在实数集R上的单调性呢? 不妨认为a>1, 要讨论指数函数y=ax在实数集R上的单调性,根据单调性的定义,就是要在R上任取两个数x1,x2,且x1>x2,进而判断ax1-ax2的正负.根据指数幂的运算性质,ax1-ax2=ax2ax1-x2-1,且ax2>0.因此要判断ax1-ax2的正负,只需判断ax1-x2-1的正负,即ax1-x2与1的大小关系.这归结为当x>0,ax与1的大小关系. 下面讨论当a>1和x>0时,ax与1的大小关系. (1)若x是正整数,则ax是x个a的乘积,因为a>1,所以ax>1; 至此,我们证明了当a>1和x>0时ax>1,从而指数函数y=axa>1在实数集R上是(严格)增函数. 以上给出了证明指数函数单调性的一个方法.除了(3)中“用有理数逼近无理数”以外均是严格的逻辑推理,而这种逼近的模糊处理方式与引入无理数指数幂的方式是一致的.我们认为,在不额外增加难度和课时的前提下,还是应该尽可能避免“看图说话”,以体现数学的严谨性.直观只能用来启发思维,不能代替证明! 函数的极值和最值是两个既与单调性密切相关,又与单调性截然不同的概念.讨论极值和最值不一定必须搞清楚函数的单调性,更不需要弄清函数在整个定义域上的单调情况. 在现行教学过程中,求函数的极值通常采取如下做法(选自北师大版选修2-2)[2]: 例3求函数f(x)=3x3-3x+1的极值. 根据x1,x2列出表3-4,分析f′(x)的符号、f(x)的单调性和极值点. 表3-4 来说,x=0是f(x)的极小值点,但是在包含x=0的任何区间内均无单调性. 2018年北京理科第18题就着重考察了极值的局部性:设函数f(x)=[ax2-(4a+1)x+4a+3]ex.若f(x)在x=2处取得极小值,求a的取值范围. 解:因为f(x)=[ax2-(4a+1)x+4a+3]·ex,所以f(2)=e2. f′(x) =[2ax-(4a+1)]ex+[ax2-(4a+1)x+4a+3]ex =[ax2-(2a+1)x+2]ex =(ax-1)(x-2)ex. 在中学阶段求函数的最值,一般(如人教A版、北师大版、苏教版)使用如下的方法[8][9]: 一般地,求函数y=f(x)的在[a,b]上的最大值与最小值的步骤如下: (1)求函数y=f(x)的在(a,b)内的极值; (2)将函数y=f(x)的各极值点与端点处的函数值fa,fb比较,其中最大的一个是最大值,最小的一个是最小值. 实际上,函数y=f(x)在区间[a,b]内的最大值fx0指的是:函数f(x)在这个区间内所有点处的函数值都不超过fx0(如下图). 由上图可以看出,极大值点也是导数的零点.因此,要想求出函数f(x)的最大值,可以首先求出f(x)的导数f′(x)的零点,然后将所有导数零点与区间端点的函数值进行比较,其中最大的值为函数的最大值.函数的最小值的求法类似[10]. 这样做的好处是,减少了对导数零点是否是极值点的讨论,而是不管导数零点是否是极值点,直接将所有导数零点与区间端点的函数值进行比较. 例如:人教A版选修2-2中[11], 这个解决问题的思路还需要借助教材中的例4,实际篇幅比现在的两倍还多.如果直接将所有导数零点与区间端点的函数值进行比较,解答过程可以如下: 这与原解答得到的结论一样,但是解决问题的过程不仅变得更加简洁,重要的是解决问题的思路更接近数学的本质.1.1 关于区分单调与严格单调的建议
1.2 关于淡化单调区间概念的建议

2 指数函数单调性的教学

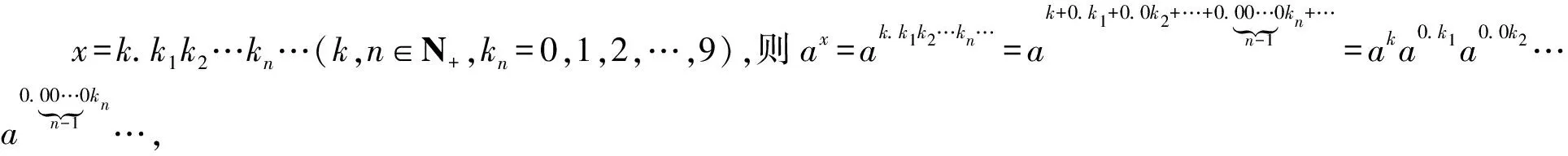
3 函数单调性与极值、最值的关系
3.1 极值不一定与单调性有关



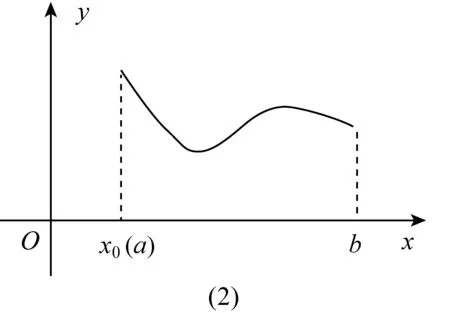
3.2 最值不一定与单调性有关