回归建模的基础与要领(Ⅱ)
——偏态分布计量资料的变换
2019-01-16胡良平
胡良平
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu812@sina.com)
1 计量资料的分布类型
1.1 计量资料的概念
测定“身高”“体重”“胸围”“血脂”等指标的数值所得到的资料,在统计学上都被称为“计量资料”。它们有一个共同特点:数值可以带小数且有度量衡单位。严格地说,任何一个计量变量的取值可以充满其取值区间,只是在实际中,满足一定的精度要求就可以了。例如,当研究者测量人的身高时,若以“厘米”为单位,通常保留到小数点后一位即可,如:165.3厘米,其中的“0.3”是估计出来的,没有必要写成“165.324568厘米”。若是计算的“中间结果”,可以保留到小数点后第6位(目的是尽可能减少计算过程中的舍入误差),但对于最终结果,一般只保留到测量工具能准确测到的下一位。
1.2 计量资料分布类型的概念[1]
将某实际问题中的一个计量变量的全部取值由小到大排序,再将它们按相等的间隔划分为若干组,然后,统计出各组中的数据个数,即“频数”。若用表格形式呈现此时的资料,它就被称为“频数分布表资料”。所谓“频数分布”,就是“频数”在各组段上是如何“分配”的;若用图形形式呈现此时的资料,它就被称为“频数分布直方图”。例如:图1所显示的直方图就被称为“正偏态分布的计量资料”。
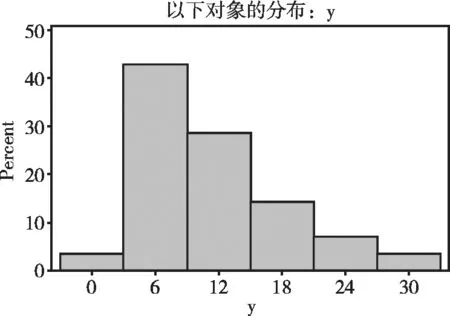
图1 30只老鼠肿瘤发展到特定尺寸所用时间(d)的频数分布直方图
由图1可知:频数最多的组位于横坐标轴上偏向“左边”的位置,右边出现了较长的“尾巴”。若采用一个叫“偏度系数g1”的公式计算,得到的结果为“g1>0”,故称具有这样频数分布的计量资料为“正偏态分布计量资料”。而图2所显示的直方图被称为“负偏态分布的计量资料”。
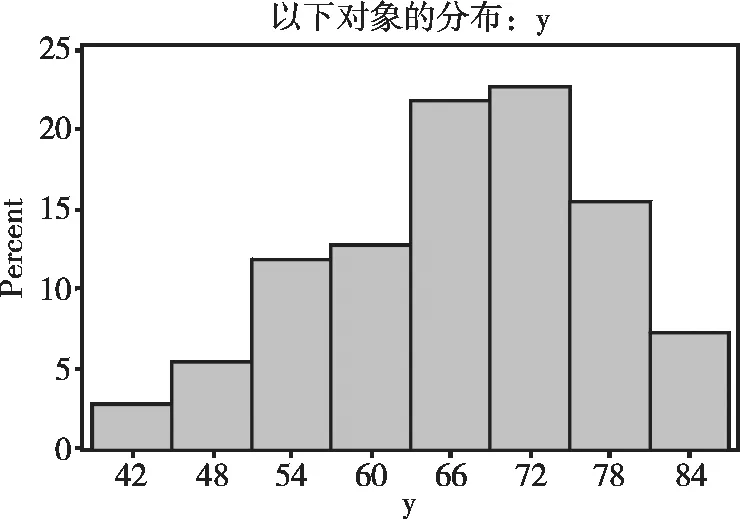
图2 某地110名健康男性体重(kg)的频数分布直方图
由图2可知:频数最多的组位于横坐标轴上偏向“右边”的位置,左边出现了较长的“尾巴”。若采用一个叫“偏度系数g1”的公式来计算,得到的结果为“g1<0”,故称具有这样频数分布的计量资料为“负偏态分布计量资料”。
实际计量资料中,还有一些的频数分布为“基本对称”分布,即“频数最多的组位于横坐标轴上基本居中的位置”。若采用一个叫“偏度系数g1”的公式来计算,得到的结果为“g1≈0”,故称具有这样频数分布的计量资料为“对称分布计量资料”,见图3。
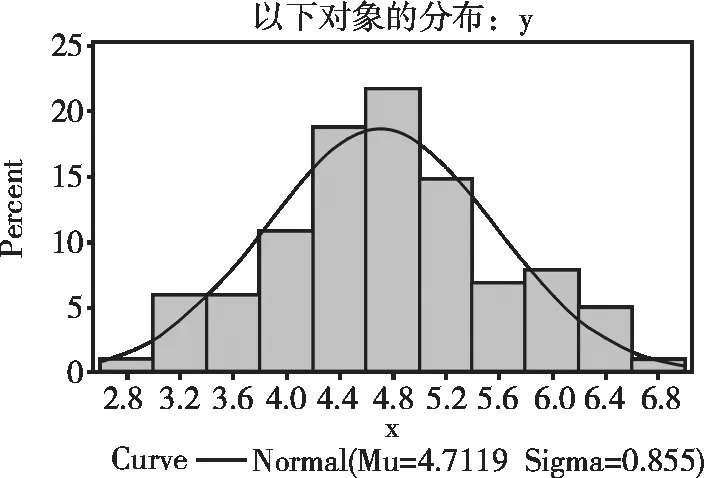
图3 由101名正常成年男子血清总胆固醇数据绘制的频数分布直方图
若图3中的光滑曲线可用公式(1)描述,则该“曲线”被称为“正态分布曲线”。
(1)
满足式(1)的曲线被称为“一般正态分布曲线”,其“均值为μ、标准差为σ”;它是单峰分布的,高峰位于横坐标轴的正中位置;它的“偏度系数g1=0”,同时,它的“峰度系数g2=0”。若“均值为0、标准差为1”,此时的正态分布就被称为“标准正态分布”。
1.3 将偏态分布计量资料变换为正态分布计量资料的必要性
在经典统计学中,无论是对计量资料进行假设检验(如Z检验、t检验、方差分析)、区间估计,还是进行简单线性回归分析或多重线性回归分析,首选的方法是“参数法”。而参数法的重要前提条件之一是来自结果变量的计量资料必须服从“正态分布”。例如,文献[2]中专门用一章篇幅详细介绍“正态分布的统计方法”。
通常,需要先对计量资料进行正态性检验。当正态性检验得出该组计量资料服从正态分布时,可以采用相应的“参数法”对计量资料进行处理;反之,则要求采用“非参数法”处理计量资料。然而,在多因素或多自变量的情况下,常没有合适的“非参数法”可运用。有时,人们习惯借助某种变量变换方法,希望经变换后的计量资料满足“正态分布”的要求,再对变换后的计量资料采取“参数法”处理。
事实上,并非所有计量资料通过某种变量变换方法变换后都能符合“正态分布”要求。若能将服从偏态分布的计量资料变换为“对称分布”的计量资料,也就很接近“参数法”的要求了。文献[2]中给出了“为对称性而变换”的方法。
1.4 常用的计量资料变换方法[2]
1.4.1 对数变换
当计量资料x呈正偏态分布时,对其进行对数变换可使其偏态状况有所减弱;有时,取对数变换后,计量资料就接近正态分布了。用y表示变换后的计量资料,见式(2)和式(3):
y= ln(x),x>0
(2)
y= ln(x+C), 部分x<0或x=0
(3)
在式(3)中,取C>max|x|,这里的x为负值,“max”为取“最大值”之意,应确保所有的“C+x”一定大于0。
1.4.2 平方根变换
当一组计量资料x的算术平均值近似等于其方差(若将此时的计量资料近似视为“计数资料”,则这样的计数资料被认为近似服从Poisson分布的计数资料[3])时,对其进行平方根变换可使其偏态状况有所减弱;有时,取平方根变换后,计量资料就接近正态分布了。用y表示变换后的计量资料,见式(4)和式(5):
(4)
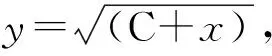
(5)
在式(5)中,取C≥max|x|,这里的x为负值,“max”为取“最大值”之意,应确保所有的“C+x”一定大于或等于0。
1.4.3 倒数变换
当计量资料x呈负偏态分布时,对其进行倒数变换可使其偏态状况减弱;有时,取倒数变换后,计量资料就接近正态分布了。用y表示变换后的计量资料,见式(6)和式(7):
y= 1/x,x>0
(6)
y= 1/(C+x), 部分x<0或x=0
(7)
在式(7)中,取C>max|x|,这里的x为负值,“max”为取“最大值”之意,应确保所有的“C+x”一定大于0。
1.4.4 Box-Cox变换(包含“幂变换”与“对数变换”)[4]
当计量资料x呈偏态分布(包括正偏与负偏两种情形)时,对其进行Box-Cox变换可使其偏态状况减弱;有时,经此变换后,计量资料就接近正态分布了。用y表示变换后的计量资料,见式(8)和式(9):
(8)
y=ln(x), λ=0
(9)
Box-Cox变换的一般形式见下面的式(10)与式(11):
(10)
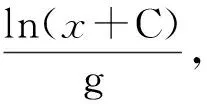
(11)
在式(10)与式(11)中,取C>max|x|,这里的x为负值或0,“max”为取“最大值”之意,应确保所有的“C+x”一定大于0;g通常取值为1。
1.4.5 变量变换的效果
值得注意的是:对一组计量资料或计数资料做任何变换,都不可能绝对保证一定能使其呈“对称分布”或“正态分布”。通常,经过合适的变量变换后,会使变换后的资料较原始资料具有更好的“对称性”。有时,可能需要相继采取多种变量变换方法。若目的是为了使变换后的资料接近“正态分布”,则必须对变换后的资料进行严格的正态性检验。只有通过了正态性检验(最好,正态性检验的结果为P>0.2;通常,P>0.1即可;但至少也应满足P>0.05)的资料,才适合选用相应的参数统计分析方法(如t检验、方差分析、简单线性回归分析或多重线性回归分析,在回归分析中,应特别强调:因变量应近似服从正态分布;然而,在统计理论上,假定“模型的误差项服从正态分布”)。
以下基于SAS中的“TRANSREG过程”[4]并采用“Box-Cox变换”将偏态分布计量资料变换为近似呈正态分布的计量资料。
2 将偏态分布计量资料变换为正态分布计量资料
2.1 将正偏态分布计量资料变换为正态分布计量资料
2.1.1问题与数据结构
【例1】给30只老鼠注射给定的肿瘤接种物,肿瘤发展到特定尺寸所用的时间(d)如下:
1.7、3.7、5.0、5.1、5.3、5.9、6.0、6.0、7.4、8.0、8.3、8.3、8.3、9.1、9.6、11.3、12.1、12.3、13.1、13.4、14.0、15.9、16.1、16.7、17.0、21.0、22.7、30.0
2.1.2 所需的SAS程序
利用下面的SAS程序创建SAS数据集并进行Box-Cox变换:
/*以下的SAS数据步程序用于创建SAS数据集a1*/
data a1;
inputy@@;
z=0;
cards;
1.7 3.7 5.0 5.1 5.3 5.9 6.0 6.0 7.4 8.0
8.3 8.3 8.3 9.1 9.6 11.3 12.1 12.3 13.1
13.4 14.0 15.9 16.1 16.7 17.0 21.0 22.7 30.0
;
run;
/*以下程序绘制a1的频数分布直方图并进行正态性检验*/
proc univariate data=a1 normal;
vary;
histogramy;
run;
/*以下程序对a1进行Box-Cox变换,求出合适的lambda值*/
/*经过Box-Cox变换后的数据存储在数据集aaa中*/
ods graphics on;
proc transreg details data=a1 maxiter=0 nozerocon
stant plots=(transformation(dependent) obp);
model BoxCox(y/ convenient lambda=-10 to 10 by 0.01)=identity(z);
output out=aaa approximations;
run;
/*以下程序绘制aaa的频数分布直方图并进行正态性检验*/
proc univariate data=aaa normal;
varty;
histogramty/normal;
run;
2.1.3 输出结果及解释
2.1.3.1 反映原始数据分布状况的结果
本例中原始数据的频数直方图见前面的图1(呈正偏态分布),此处从略。对原始数据进行正态性检验的结果为:W=0.925501、P=0.0475,说明原始数据不服从正态分布。
偏度系数与峰度系数分别为g1=1.097与g2=1.415,表明原始数据具有正偏态(偏度系数明显大于0)和尖翘峰(峰度系数明显大于0)分布。
2.1.3.2 对原始数据作Box-Cox变换的结果
求得公式(8)中的参数λ为“0.29”,对经Box-Cox变换后的数据作正态性检验,得到:W=0.971648、P=0.6254,说明经Box-Cox变换后的数据服从正态分布。绘制经Box-Cox变换后数据的频数直方图,见图4。
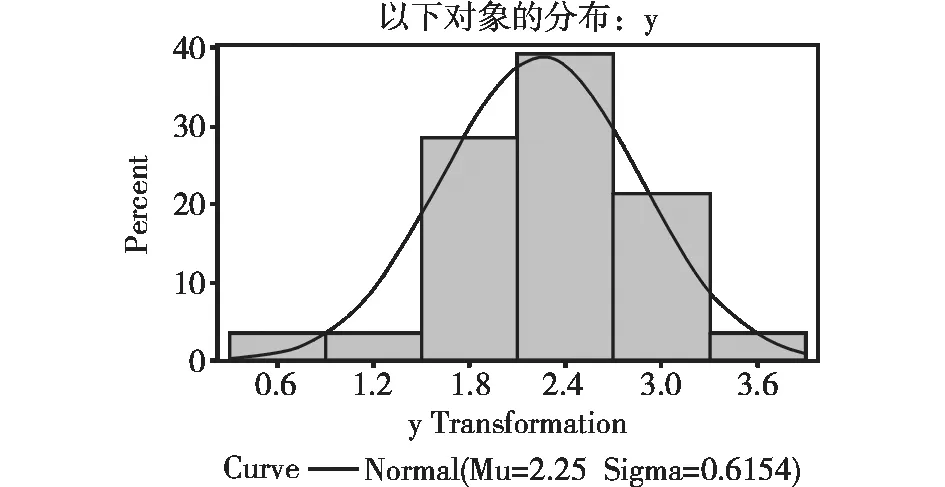
图4 经Box-Cox变换后的30只老鼠肿瘤发展到特定尺寸所用时间(d)的频数分布直方图
2.2 将负偏态分布计量资料变换为正态分布计量资料
2.2.1 问题与数据结构
【例2】某研究者收集到某地110名健康成年男性的体重(kg)数据如下:
43.5、70.0、45.0、45.0、46.5、69.5、58.0、68.0、66.5、70.1、67.0、66.5、68.0、59.0、66.0、68.0、69.8、68.8、67.0、55.5、51.5、52.5、61.0、58.0、47.5、53.0、53.0、54.0、59.0、54.0、46.0、54.0、55.0、57.0、52.0、52.0、50.0、54.0、62.5、54.5、65.0、61.5、60.5、60.0、68.5、67.0、70.0、67.0、75.0、70.5、64.5、68.0、72.0、63.0、63.5、64.0、65.0、74.5、72.5、67.5、72.0、69.0、61.5、69.0、60.0、40.0、71.2、74.0、71.0、69.5、69.0、61.0、70.3、68.5、64.5、70.5、73.0、65.0、67.5、71.0、79.0、80.0、72.5、79.0、75.2、81.0、82.0、75.0、73.0、77.0、80.0、81.5、42.0、77.0、75.3、81.0、83.0、74.5、80.0、75.5、80.0、77.0、75.0、61.0、79.0、81.5、78.0、73.5、81.9、85.0
试呈现原始数据的分布情况,并对其进行变量变换,使其接近正态分布。
2.2.2 所需要的SAS程序
利用下面的SAS程序创建SAS数据集并进行Box-Cox变换:
/*以下的SAS数据步程序用于创建SAS数据集a1*/
/*在原始数据中增加一个新变量z,它是原始数据*/
/*取倒数变换后再乘以1000得到的结果*/
data a1;
inputy@@;
z=(1/y)*1000;
cards;
43.5 70.0 45.0 45.0 46.5 69.5 58.0 68.0 66.5 70.1 67.0 66.5 68.0 59.0 66.0 68.0 69.8 68.8 67.0 55.5 51.5 52.5 61.0 58.0 47.5 53.0 53.0 54.0 59.0 54.0 46.0 54.0 55.0 57.0 52.0 52.0 50.0 54.0 62.5 54.5 65.0 61.5 60.5 60.0 68.5 67.0 70.0 67.0 75.0 70.5 64.5 68.0 72.0 63.0 63.5 64.0 65.0 74.5 72.5 67.5 72.0 69.0 61.5 69.0 60.0 40.0 71.2 74.0 71.0 69.5 69.0 61.0 70.3 68.5 64.5 70.5 73.0 65.0 67.5 71.0 79.0 80.0 72.5 79.0 75.2 81.0 82.0 75.0 73.0 77.0 80.0 81.5 42.0 77.0 75.3 81.0 83.0 74.5 80.0 75.5 80.0 77.0 75.0 61.0 79.0 81.5 78.0 73.5 81.9 85.0
;
run;
/*以下程序绘制a1中原始数据y和倒数变换后z的频数分布直方图并进行正态性检验*/
proc univariate data=a1 normal;
varyz;
histogramyz;
run;
/*以下程序在数据集a1中增添w=0的一列,形成数据集a2*/
data a2;
set a1;
w=0;
run;
/*以下程序对a2进行Box-Cox变换,求出合适的lambda值*/
/*经过Box-Cox变换后的数据存储在数据集aaa中*/
ods graphics on;
proc transreg details data=a2 maxiter=0 nozerocon
stant plots=(transformation(dependent) obp);
model BoxCox(z/ convenient lambda=-10 to 10 by 0.05)=identity(w);
output out=aaa approximations;
run;
/*以下程序绘制aaa的频数分布直方图并进行正态性检验*/
proc univariate data=aaa normal;
var tz;
histogram tz/normal;
run;
2.2.3 输出结果及解释
2.2.3.1 反映原始数据分布状况的结果
本例中的原始数据y的频数直方图见前面的图2(呈负偏态分布),此处从略。对原始数据y进行正态性检验的结果为:W=0.967065、P=0.0080,说明原始数据y不服从正态分布。
偏度系数与峰度系数分别为g1=-0.495,g2=-0.385,表明原始数据具有负偏态(偏度系数明显小于0)和平阔峰(峰度系数明显小于0)分布。
本例中的原始数据经倒数变换后的数据z的频数分布直方图见图5(呈正偏态分布)。
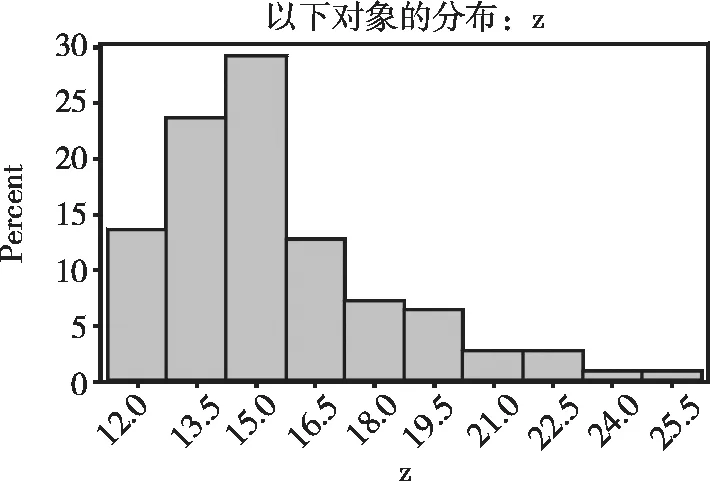
图5 本例数据经倒数变换后的数据z的频数分布直方图
对经倒数变换后的数据z进行正态性检验的结果为:W=0.892042、P<0.0001,说明经倒数变换后的数据z不服从正态分布。
偏度系数与峰度系数分别为g1=1.237,g2=1.242,表明经倒数变换后的数据z具有正偏态(偏度系数明显大于0)和尖翘峰(峰度系数明显大于0)分布。
2.2.3.2对经倒数变换后的数据z作Box-Cox变换的结果
求得公式(8)中的参数λ为“-2.2”,对经Box-Cox变换后的数据作正态性检验,得到:W=0.980521、P=0.1079,说明经Box-Cox变换后的数据服从正态分布。
绘制经Box-Cox变换后的数据的频数分布直方图,见图6。
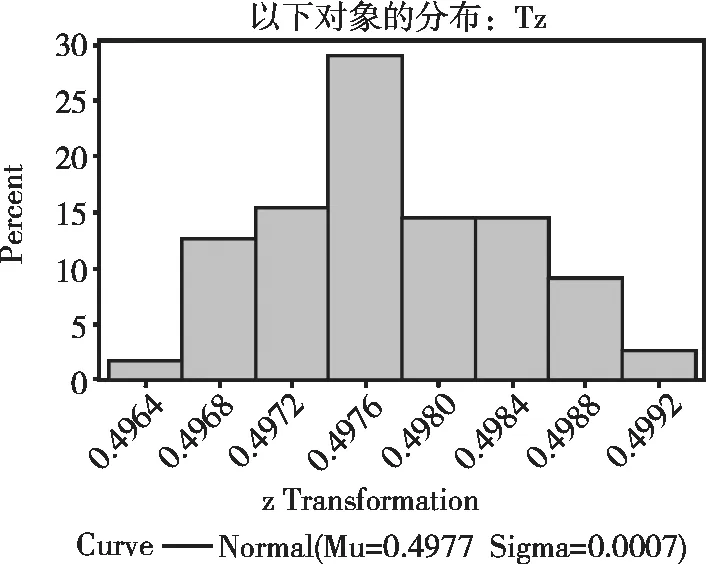
图6 经Box-Cox变换后的某地110名健康男性体重(kg)的频数分布直方图
