隧穿量子点分子的Wigner-Yanase偏态信息

叶 芳,白志达,周青春

(江苏科技大学 理学院, 镇江 212003)

在过去的十多年里,与量子信息紧密相关的量子通信技术得到飞速发展,从而使得借助于客体状态及某个特定物理量实现量子信息的量化显得格外重要．但信息量的确定仍然是一个有待探究的问题．研究显示,Wigner-Yanase偏态信息[1]是度量量子信息的一种有效方法,因其符合信息度量的所有要求[2],在其他领域被人们拓展[3-5]．Wigner-Yanase偏态信息度量量子信息的方法利用密度算符与观察量算符的不对易程度,可以建立起量子的Cramer-Rao不等式与扩展的不确定度关系,估计量子态演化的速度[6],以及解释量子测量和统计干涉的关系．另外,该信息还能够用来揭示纠缠的量子特性[7-8]．

随着对量子点分子的深入研究,了解到量子点分子虽然拥有着与常规分子相似的特点,但又区别于常规分子的特有性质,使其在将来的量子和光子计算机方面拥有越来越高的应用价值．因此,近年来量子点分子的研究以及发展前景引起了人们的密切关注[9]．人们利用全量子理论研究了隧穿量子点分子J-C模型的Berry相位[10],隧穿量子点分子模型与光场相互作用的熵特性[11],以及利用Pegg-Barnett相位理论研究了隧穿量子点分子模型与光场相互作用系统中光场的相位特性[12]等．目前,对于隧穿量子点分子的Wigner-Yanase偏态信息的研究还未见报道,文中运用全量子理论研究了隧穿量子点分子的Wigner-Yanase偏态信息时间演化与布居数演化．

1 偏态信息的计算

1.1 Wigner-Yanase偏态信息

从信息论的角度出发,Wigner和Yanase提出了Wigner-Yanase偏态信息(以下均简称偏态信息)[13]．如果给定体系密度矩阵ρ与可观测量Ak,则该体系的偏态信息定义如下[1]:

(1)

上式表明偏态信息是通过ρ与Ak的非对易关系进行信息量度量的．对于三能级系统,其赝自旋算符可以构造如下:

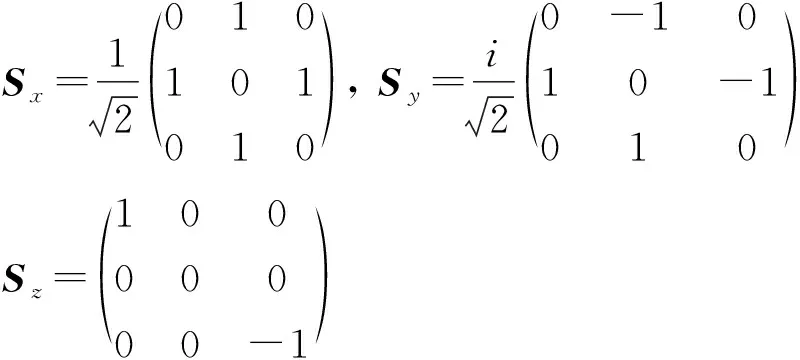
(2)

则总偏态信息为3个分量偏态信息之和，I总=I(ρ,Sx)+I(ρ,Sy)+I(ρ,Sz)．

若体系处于最大混合态:ρ=1/3(|0><0|+|1><1|+|2><2|),则I=0.

1.2 模型及理论计算

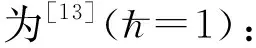
H=Te(|1><2|eiδ1t+|2><1|e-iδ1t)+

Ω(|0><1|e-iδ2t+|1><0|eiδ2t)

(3)

式中：δ1=ε1-ε2,δ2=ε1-ε0-ω(δ2≤ω)为隧穿量子点分子—光场失谐量,ε0,ε1,ε2为|0>,|1>,|2>能级所对应的能量,ω为激光频率．假设δ1=0,δ2=0，则该哈密顿量的矩阵表示可以写为:

(4)

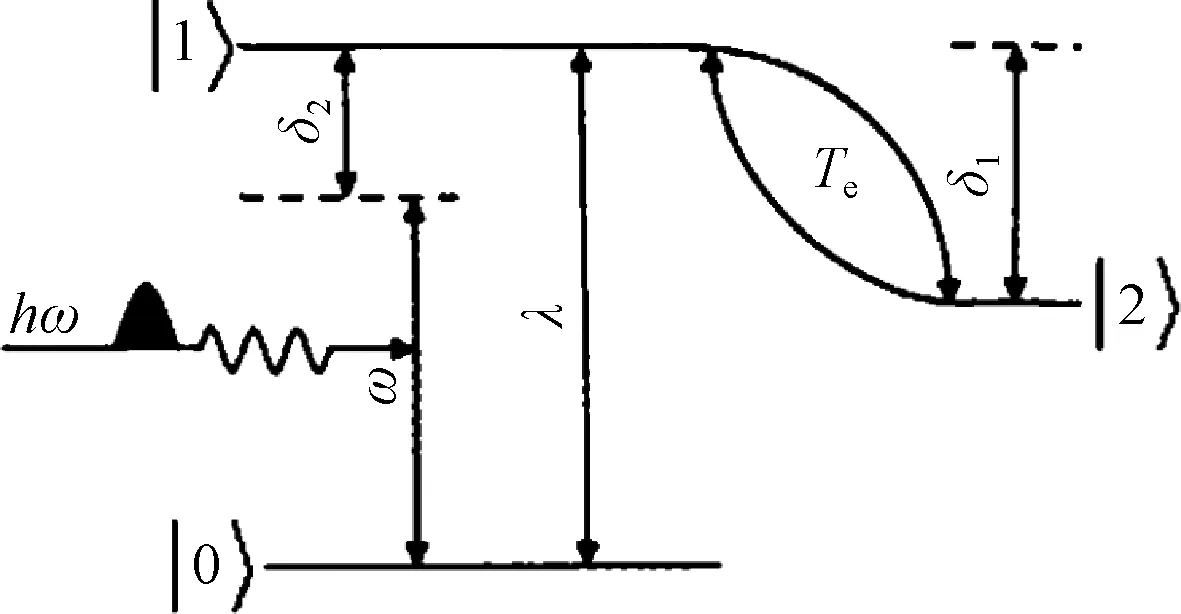
图1 隧穿量子点分子与光场相互作用模型Fig.1 Model of the tunneling quantum dotmolecule interacting with a light-filed

设体系初始状态处于基态|0>,即|ψ(0)>=[1,0,0]T,带入薛定谔方程可得:

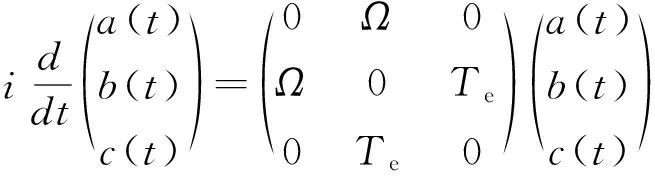
(5)

解得:

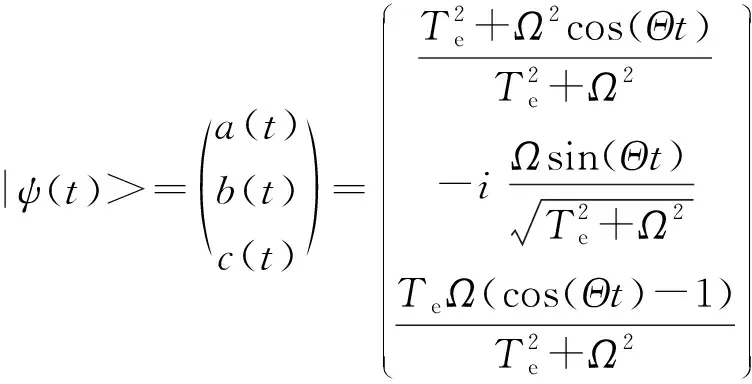
(6)

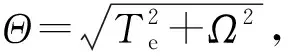
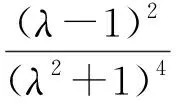
(7)

式中:

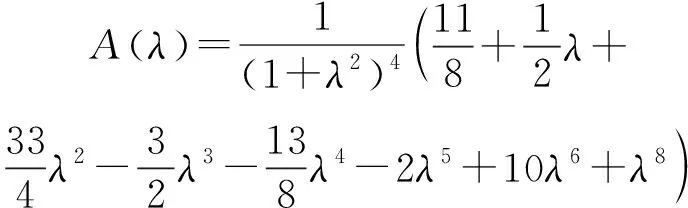
(8)

B(λ)=-λ-8λ2-15λ3-8λ4

(9)

D(λ)=λ-λ3

(10)

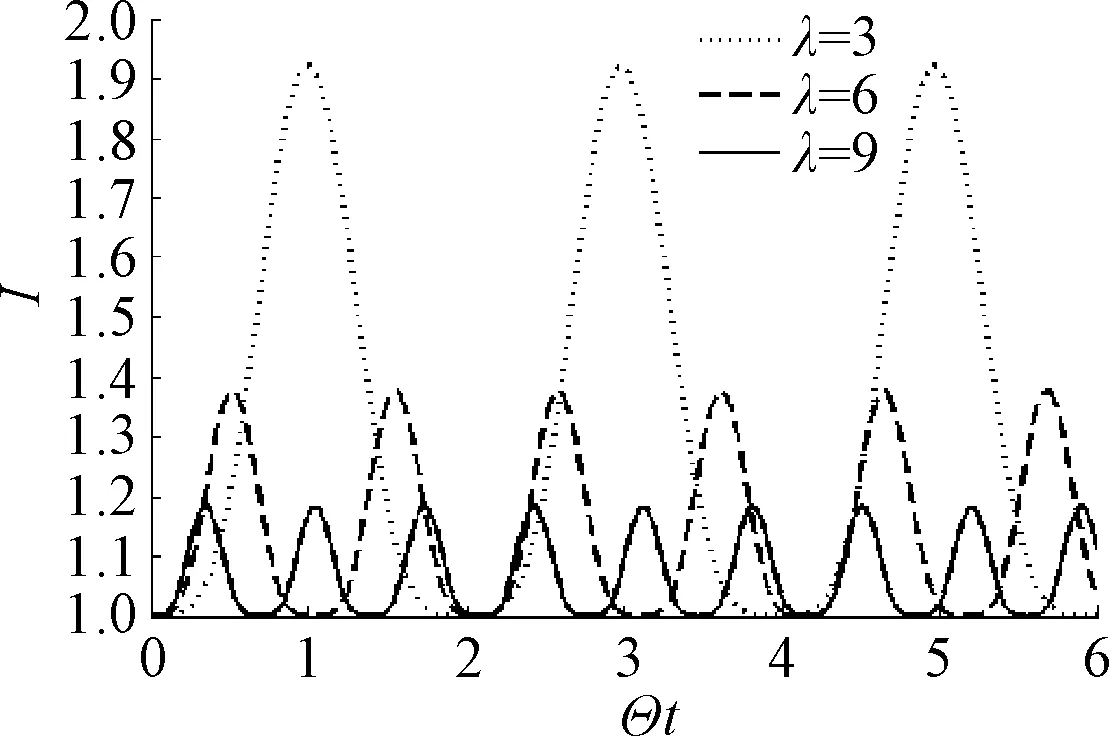
图2 经典光场情况下的Wigner-Yanase偏态信息Fig.2 Wigner-Yanase skew information underthe classical optical field

若考虑腔场为量子场,则图1中隧穿量子点与量子光场的相互作用的哈密顿量可以写为:

H=Te(|1><2|eiδ1t+|2><1|e-iδ1t)+

Ω(a+|0><1|e-iδ2t+a|1><0|eiδ2t)

(11)

式中a(a+)为光场的湮灭和产生算符．

设初始时刻光场处于相干态,量子点分子处于能级|1>,则初始时刻隧穿量子点分子和光场组成的系统态矢量可写为:

(12)

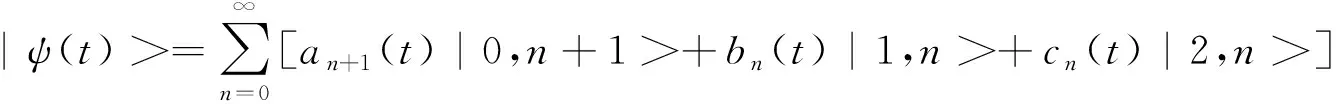
(13)

假设失谐量δ1=δ2=Δ,则由薛定谔方程容易得到:

(14)

利用初始条件(12)，解得:

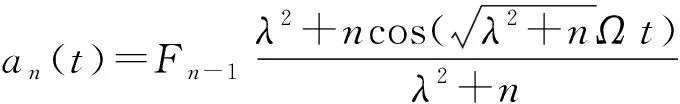
(15)

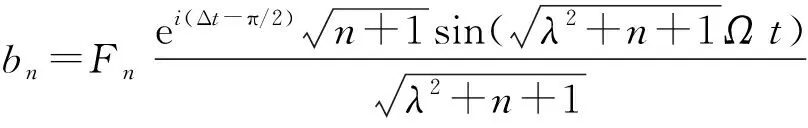
(16)

(17)

由式(15～17)，以及将式(13)写成密度矩阵形式,并且对光场求迹,可以得到隧穿量子点的约化密度算符:

(18)

带入偏态信息表达式(1)中可以求得量子光场情况下偏态信息的时间演化．

2 数值计算及分析

2.1 各能级上布居数时间演化与参数的关系

取Δ=0,=25,λ=1，对式(18)进行数值计算,得到能级|0>、|1>、|2>上布居数的时间演化图像(图3(a～c));取Δ=0,=25,λ=5，对式(18)进行计算,得到能级|0>、|1>、|2>上布居数的时间演化图像(图3)．

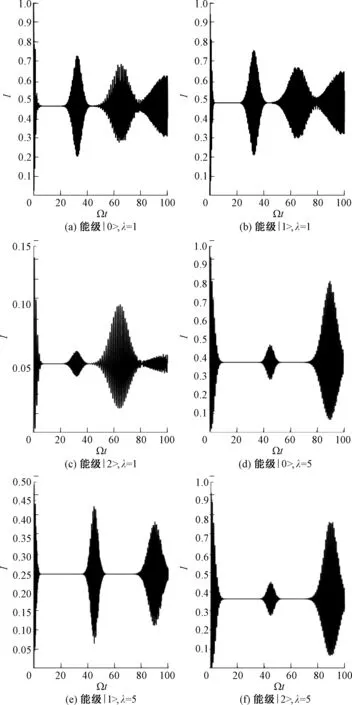
图3 各能级上布居数时间演化与λ的关系Fig.3 Relationship between the timeevolution of population and λ

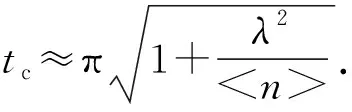
2.2 量子点分子的偏态信息

图4为λ=1和λ=5时,偏态信息随时间演化的图像．与图3中的布居数反转图像对比可知,在布居数反转塌缩区间,偏态信息的演化曲线是光滑的;而在布居数反转的复原区间,偏态信息振荡频率很大,且与布居数反转类似，具有明显的包络线．此外,偏态信息的极大值逐渐减小．此处振荡与布居振荡都源于密度矩阵的迅速振荡,物理上是式(15～17)中不同频率分量相干叠加干涉的结果．比较图4(a)和(b)可以看出对于较小的隧穿强度,布居数反转塌缩的区域对应于偏态信息恢复到极大值的区域,表明该时区内量子点分子向纯态演化,场与原子趋向于退纠缠,这与J-C模型情况类似[14]．布居数反转恢复的区域对应于偏态信息取极小值的区域,表明场与量子点分子高度纠缠．而对于较大的隧穿强度,偏态信息极大值可以出现在布居振荡复原区．

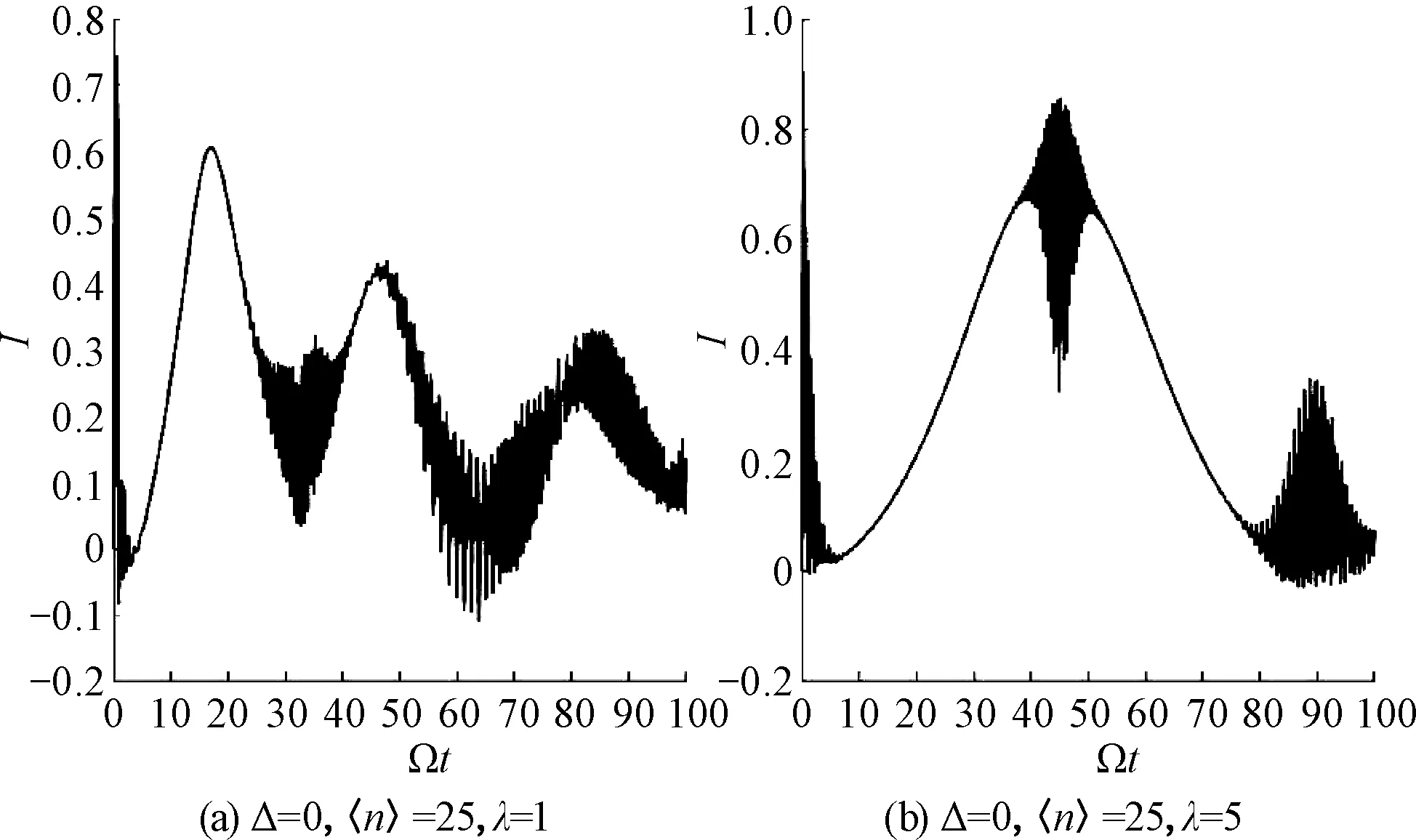
图4 偏态信息时间演化与λ的关系Fig.4 Relationship between skew information and λ

从图5所给出的偏态信息的演化曲线可以看出,随着平均光子数的增大，偏态信息的振荡周期逐渐增大．

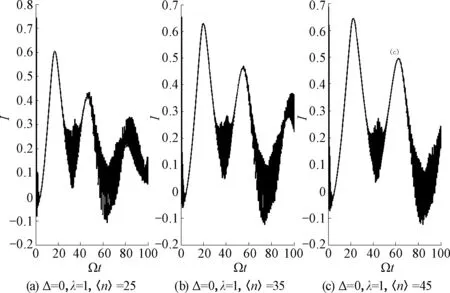
图5 偏态信息时间演化与平均光子数〈n〉的关系Fig.5 Relationship between skew informationand mean photon number 〈n〉

图6为不同失谐量情况下的偏态信息时间演化图像,可以看出随着失谐量的增大,布居数反转塌缩区域对应的光滑曲线振荡次数逐渐增多．

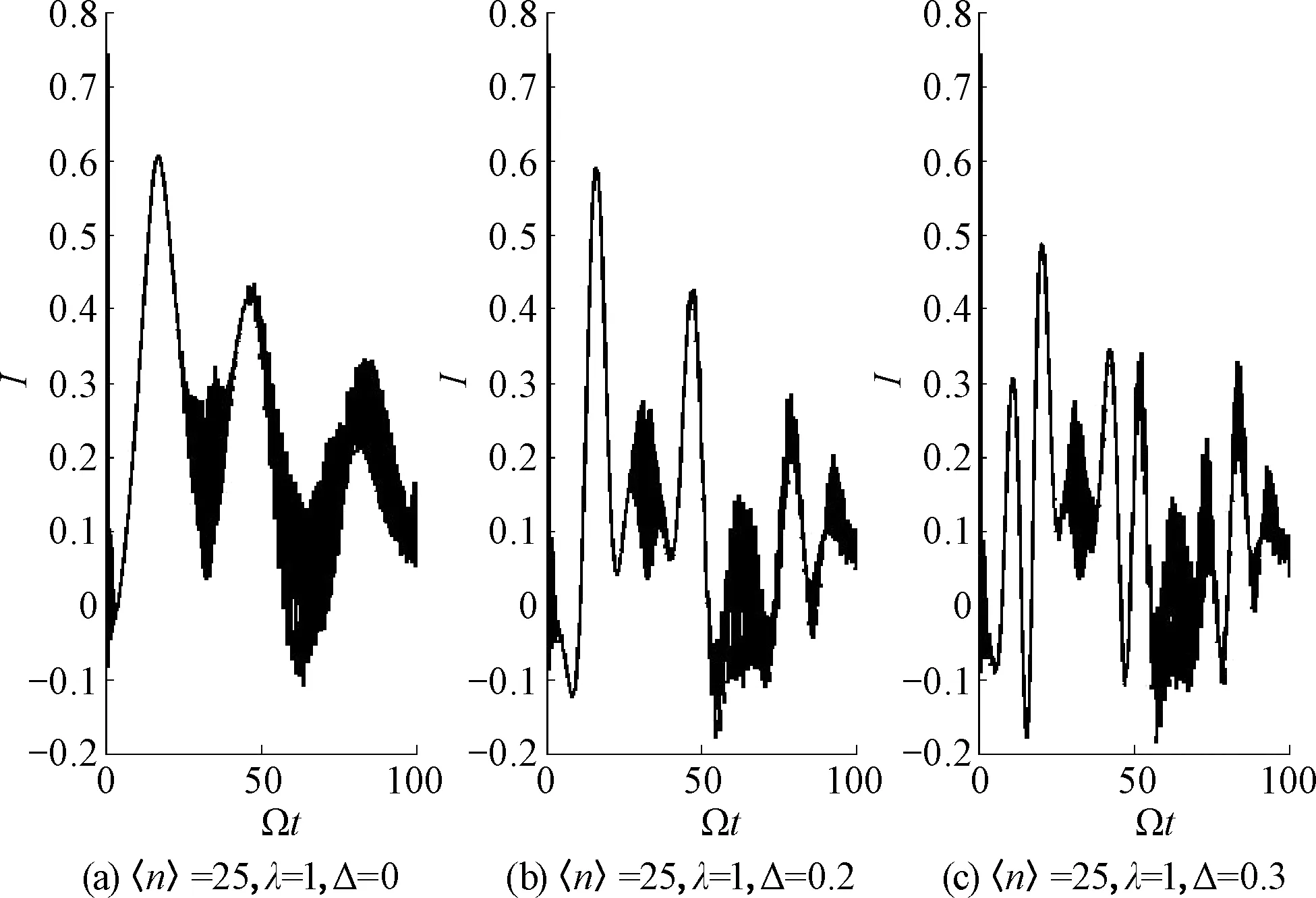
图6 偏态信息时间演化与失谐量Δ的关系Fig.6 Relationship between skewinformation and detuning Δ

3 结论

(1) 文中利用全量子理论,研究了隧穿量子点分子的Wigner-Yanase偏态信息,具体讨论了各能级上布居数时间演化与耦合系数的关系,同时分析了平均光子数〈n〉和失谐量Δ，以及耦合系数λ对Wiger-Yanase偏态信息的影响．结果发现，各个能级上的布居数演化呈现出典型的塌缩复原现象,耦合系数λ增大,塌缩时间增长．偏态信息演化周期随平均光子数〈n〉的增大而增大,失谐量会影响布居数塌缩区间偏态信息的振荡次数．

(2) 在布居数反转塌缩区间,偏态信息的演化曲线是光滑的;而在布居数反转的复原区间,偏态信息振荡频率很大,与布居数反转类似，具有明显的包络线;并且对于较小的隧穿强度,布居数反转塌缩的区域对应于偏态信息恢复到极大值的区域,布居数反转恢复的区域对应于偏态信息取极小值的区域;而对于较大的隧穿强度,偏态信息极大值可以出现在布居数振荡复原区．