基于贝叶斯网稀疏结构学习的信用影响因素结构发现

郭 珉，石洪波，程 鑫

(山西财经大学 信息管理学院，山西 太原 030031)

一、引言

大数据情景下，影响个人信用的因素复杂多样，挖掘影响因素之间隐藏的内在关联及规律成为信用风险及信用监管研究的关键任务。基于数据驱动的贝叶斯网络可以通过多维变量的联合概率给出变量间结构关系的全局描述，甚至在特定情况下可以揭示变量间的因果关系。因此，贝叶斯网络在遗传、生物、医疗健康、金融、风险防控、信用评估等领域有着较为广泛的应用[1]。

但是，传统贝叶斯网络学习方法在面对海量数据，特别是高维数据时遇到了挑战。(1)具有p个节点的贝叶斯网络最多可能有p(p-1)/2条边，则学习贝叶斯网络结构要在大小为2O(p2)的解空间搜索最优解。随着个人信用影响因素的增加，导致解空间呈指数倍扩张，传统结构学习方法出现计算量大、有效性差甚至不可行等问题。(2)实际信用研究中连续变量通常不服从正态分布，需要先转换为离散变量，然后利用离散贝叶斯网络学习变量间依赖关系。与同等规模的高斯贝叶斯网相比，高维环境下构建离散贝叶斯网要复杂得多，参数个数特别多，易导致过拟合、泛化及解释能力变差等问题[2]。

基于multi-logit模型的离散贝叶斯网稀疏结构学习方法一定程度上能有效缓解上述问题，Fu等已证明当节点个数固定时，该方法面对高维甚至p≫n的数据，学到的稀疏网络结构和参数具有渐进一致性[3]。目前已有学者将其应用于生物数据的研究，本文首次尝试将其应用于信用领域，即构建个人信用影响因素之间的全局结构关系，用稀疏有向无环图(Directed Acyclic Graph，DAG)可视化个人特征与信用类型重要的依赖关系，并用条件概率表度量信用影响因素节点间直接或间接的依赖程度。接着，由于本文的研究主旨为信用影响因素间关系的结构发现，同时稀疏算子可以调控稀疏贝叶斯网结构的稀疏度，因此基于不同稀疏算子构成的解路径，本文尝试性地探讨了稀疏模型选择标准。最后，根据最终得到的最优网络结构，通过贝叶斯网推理量化分析关键影响因素对信用类型的直接及间接影响。

二、文献综述

(一)信用领域影响因素间关系的相关研究

大数据技术的发展和数据可获得性的增加，导致影响个人信用风险的因素具有高维和非线性的特点。目前，研究信用风险变量间关联关系主要从两个方向进行，一个方向是通过各类回归模型研究影响因素与目标变量之间的关系，如线性回归、Logistic回归、多分类有序Logit回归、Probit回归、分层回归等[4-6]。这类模型一般都有类似线性关系、正态分布、多重特征独立等比较严格的假设前提，因此模型的使用效果受到影响。并且，大多数文献研究低维变量间的影响关系，当面向高维数据时，已有方法大多存在模型解释性差的问题。采用稀疏学习方法改进现有回归方法，则一定程度上可以缓解上述问题。李太勇等使用稀疏贝叶斯模型实现特征选择和个人信用评估，模型本质为基于贝叶斯先验的稀疏线性回归[7]。方匡南等基于MCP罚和网络结构罚改进了传统Logistic回归以弥补其在信用评估中的缺陷[8]。但是，以上方法仅从局部角度反映单变量对目标变量的独立影响，在网络结构发现方面的能力略显不足，而贝叶斯网能从全局角度描述所有变量间的依赖关系，既包括单变量的独立影响，也包括多变量的联合影响。

另一个研究方向是相关分析，即通过引入统计指标量化变量间的相关程度，并将相关分析结果作为信用评估统计模型或机器学习模型前期特征选择的依据。信用影响因素常采用的相关分析方法主要有：关于两变量的各类相关系数和相关性检验、基于互信息的非线性相关分析以及基于距离的相关性计算，这些相关性分析反映了变量两两之间直接的线性或非线性关系，但不能从全局刻画所有变量间的结构关系。贝叶斯网结构学习通过DAG不仅可以描述不同因素间的影响路径及内在机制，而且能够抓取影响目标变量的直接和间接因素。

(二)传统贝叶斯网在信用领域中的应用

贝叶斯网和贝叶斯分类器不同，贝叶斯网可以用于结构发现，也可以用于预测，而贝叶斯分类器主要用于分类预测。朴素贝叶斯分类器较早应用于信用评估，其前提假设较为严格，要求特征变量相互独立，且无法提供反映变量依赖关系的网络结构。树增强型贝叶斯分类器放宽了前者的前提条件，但只能表达树状的网络结构，而贝叶斯网络则可以基于数据生成复杂的网络结构。

目前已收集的基于贝叶斯网络的应用类文献广泛采用K2算法构建贝叶斯网络结构，然后利用贝叶斯网络推理结果进行分类预测。然而，由于无法获得具体问题的领域知识，K2算法若错误设定网络节点序则会严重降低学习质量，同时它还要求能正确指定每个节点最大父节点数。针对K2算法难以确定节点顺序的问题，简敏组合遗传算法和K2算法以构造贝叶斯网络模型，实现个人信用评估[9]。也有学者采用其他方法学习贝叶斯网结构。例如，裴平等以大数据征信为视角，采用对数似然损失+贪婪搜索算法获取信用评价模型的DAG，并利用贝叶斯估计学习贝叶斯网参数，但该方法搜索最优解的计算成本相当大，并需掌握相关领域知识对网络结构提前进行一定的限定以获得全局概率图[10]。以上贝叶斯网结构学习方法主要适用于小型贝叶斯网络，若刻画大中型复杂贝叶斯网结构时可能不可行，而贝叶斯网稀疏结构学习则既能简化网络结构又能保留数据所蕴含的重要信息。

(三)贝叶斯网稀疏结构学习相关研究

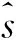
得益于高维线性回归稀疏理论的发展，早期贝叶斯网稀疏结构的研究往往从高斯贝叶斯网入手。Shojaie等在已知变量序的前提下，将学习高斯贝叶斯网结构的问题分解为一组带1罚的线性回归模型[11]。但是，实际问题的研究中往往无法获知变量序的先验信息，因此其应用推广受到限制。在此基础上，Fu等开展深入研究，在变量序未知时即可利用带1罚的最大似然估计得到稀疏网络[12]。带1罚的最大似然估计量为有偏估计，无法实现一致的模型选择。为了减少偏差，Aragam等扩展Fu的工作，使用凹罚代替1罚估计最大似然以得到一致的估计量[13]，这些高斯贝叶斯网稀疏学习方法已被成功用于生物、遗传、脑科学等领域的研究。

但是，信用涉及数据往往显示负偏或厚尾的特征[14]，高斯贝叶斯网关于数据正态分布的假定通常失效。同时，由于数据所蕴含的依赖关系并不总是线性关系，高斯贝叶斯网抓取线性关系时所用的条件独立性检验和网络评分方法，在检测非线性关系时往往效果较差，因此研究信用问题时采用离散贝叶斯网络不失为好的选择。但是，高维背景下离散贝叶斯网稀疏方法在构建优化目标函数及稀疏求解时，与高斯贝叶斯稀疏网相比难度要更大，更具挑战性。Fu等针对离散数据学习贝叶斯网稀疏结构，没有按照多项式分布构建学习模型，而是基于multi-logit回归创建节点关于父节点的条件概率，大幅减少网络参数数量，并且通过求解一个带自适应组稀疏罚的似然目标函数抓取数据蕴含的稀疏网络结构[3]。

使用稀疏罚学习贝叶斯网稀疏结构时，稀疏化算子的取值常常决定模型的性能。当贝叶斯网的学习目标为分类预测时，一般采取交叉验证选取泛化预测误差最小的稀疏化算子；当贝叶斯网的学习目标为稀疏结构发现时，由于具有较小预测误差的网络往往具有较多的边，故学者们尝试采用不同的标准确定最优模型的稀疏化算子，如Shojaie等构建基于错误选择的方法确定稀疏化算子[11]。本文首次尝试将Fu等提出的稀疏DAG学习方法用于信用影响因素稀疏结构的发现，并探讨最优稀疏结构的选择标准，最后分析信用相关变量间的直接或间接影响。

三、基于multi-logit的贝叶斯网稀疏结构学习[3]

(一)贝叶斯网基本概念

贝叶斯网被定义为一个有向无环图，记为G=(V，E)，其中节点集V={1，2，…，p}表示随机变量集X={X1，X2，…，Xp}，边集E={(j，i)∈V×V：j→i，j≠i}为G中边的集合，元素(j，i)表示存在一条从Xj到Xi的有向边，但图中不允许出现环，Xj称为Xi的父节点，Xi是Xj的子节点。已知G的结构，随机变量{X1，X2，…，Xp}的联合概率可被分解为：

(1)

其中Pa(Xi)={Xj：Xj→Xi∈E}表示节点Xi的父节点集。

(二)基于多项式模型的离散贝叶斯网

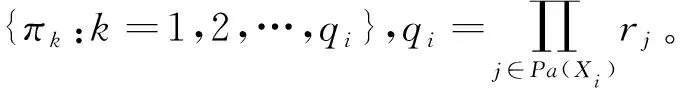
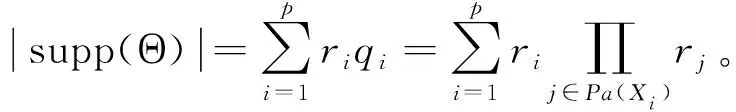
(三)基于multi-logit回归的贝叶斯网稀疏结构学习

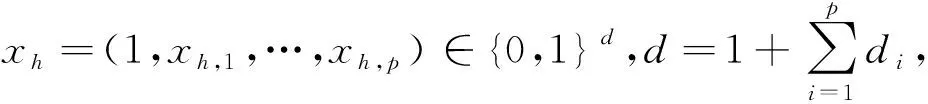
pjl(xh)P(Xj=l|xh)

(2)

其中βjl0为截距项，βjl·=(βjl0，βjl1，…，βjlp)∈Rd，βjli∈Rdi表示预测Xj水平为l时Xi的系数向量。对于所有的水平l，如果Xi∉Pa(Xj)，那么有βjli=0。为了使模型可识别，对截距施加约束：βj10=0，j=1，2，…，p。

定义：βj·i=(βj1i，…，βjrji)∈Rdirj表示Xi对Xj影响的系数向量；βj·0=(βj10，…，βjrj0)∈Rrj为预测Xj时的截距向量。令β=(βj·i)1≤j≤p，0≤i≤p为离散贝叶斯网络参数向量，则根据式(1)、式(2)离散贝叶斯网结构学习的目标函数，即对数似然函数(β)，可写为：

(3)

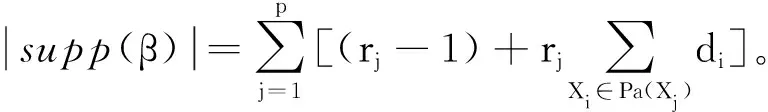
为了得到稀疏的贝叶斯网结构，需要给式(3)中对数似然函数增加一项关于网络结构的稀疏罚。离散贝叶斯网中有下面的等价成立：

βj·i=0⟺Xi∉Pa(Xj)

(4)

式(4)意味着对于离散贝叶斯网络，集合{Xi∶βj·i≠0}给出了Xj的父节点集合，反之，如果βj·i=0，则意味着从Xi到Xj不存在边。由于传统的L1正则化惩罚项只针对贝叶斯网参数β中每个元素实现惩罚，而不是针对边施加惩罚，因此它不适用于离散贝叶斯网稀疏结构学习；如果能对βj·i∈Rdirj整体施加正则化惩罚，那么即可实现网络结构中边的稀疏性学习，因此选择自适应组Lasso罚(adaptive group Lasso penalty)实现对向量βj·i整体的惩罚，获得网络结构一致性估计。最终基于multi-logit的离散贝叶斯网稀疏结构学习的目标函数为：

(5)

其中：(ωji)p×p为权重矩阵；λ>0为稀疏算子，其值越大，学到的网络结构越稀疏。ωji和λ的选取参见Fu等人的研究[3]。

(四)稀疏求解算法机理

式(5)为非凸优化问题，求精确解不可行。坐标下降算法为高维背景下求解优化问题常用的方法。式(5)稀疏求解算法将贝叶斯网DAG约束与坐标下降算法相整合，搜索目标函数局部极值。它由两层迭代组成：在外层，循环遍历全部节点对，更新边的有效集(包括边的方向)，直到满足终止条件停止循环；在内层，将外层循环每次学到的边的有效集合作为优化问题的初始值，循环遍历每条边的参数求解最小化问题[13]。

稀疏求解算法机理可表示为：

1.不停执行外层循环，直到满足终止条件结束循环。

2.外层循环。由于贝叶斯网络的无环性约束，故βi·j、βj·i(i≠j)不能同时为非零。针对每个节点对(i，j)，i≠j，执行下面步骤：

1)固定其他参数不变，求解关于块(βi·j，βj·i)的最小化目标函数(式(5))。

2)如果边i→j(或j→i)导致图出现环，则令βj·i=0(或βi·j=0)，更新βi·j(或βj·i)。

3)反复执行内层循环，直到收敛。

3.内层循环。依次循环遍历E中的每条边，求解关于βi·j的最小化问题。

四、个人信用影响因素稀疏结构关系研究

(一)数据来源和预处理

本文选取某公开信用数据集进行实证研究[注]数据来源网站：http://archive.ics.uci.edu/ml/datasets/Statlog+(German+Credit+Data)。，数据包括1 000条样本，20个属性变量和1个表示“好”、“坏”客户的类标签。属性包括7个数值属性和13个分类属性，涉及客户基本人口特征、工作、信用、财产收入等信息，具体包括：现有支票账户状况(V1)、贷款期限(V2)、信贷记录(V3)、贷款目的(V4)、信贷金额(V5)、储蓄账户/债券(V6)、工作年限(V7)、分期付款占可支配收入百分比(V8)、婚姻状况与性别(V9)、其他共同贷款者/担保人(V10)、现居住时间(V11)、资产(V12)、年龄(V13)、其他分期付款计划(V14)、住房情况(V15)、在本银行已有贷款数目(V16)、工作状况(V17)、提供生活保障的人数(V18)、电话(V19)、是否外籍劳工(V20)、客户类型(V21)。学习贝叶斯网稀疏结构之前，需首先进行数据预处理。该信用数据集数据完整，故不需填补缺失值。主要的数据预处理工作如下：

1.不平衡数据处理。由于数据集中好坏客户分别为700、300，表现出明显的不平衡性。离散贝叶斯网由于参数个数较多对样本复杂度要求较高，因此为了避免信息损失采用过抽样技术实现不平衡处理，具体为：利用bootstrap技术随机抽取300条坏客户样本与原始坏客户样本合并成600条样本，再将其与700条好客户样本合并为新的信用数据集，总计1 300条样本。

2.连续变量离散化。信用数据中部分连续变量表现出负偏或厚尾特征。如图1所示，变量V2、V5、V13经验分布不对称，显示出较强的偏斜程度，且无法获得变量真实分布，所以此类数据不适合采用高斯贝叶斯网或混合贝叶斯网方法建模，需对其离散化构建离散贝叶斯网。同时，V2、V5、V13分布不均匀且均存在离群点(图2)，因此等宽离散化或等频离散化方法并不适用。本文选择基于最小熵的有监督离散化，能结合客户类型信息实现连续变量的联合离散化。

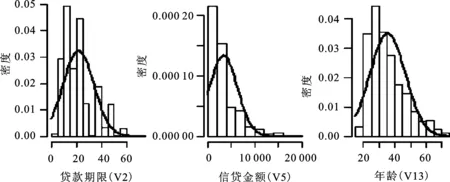
图1 变量V2、V5、V13的经验分布图

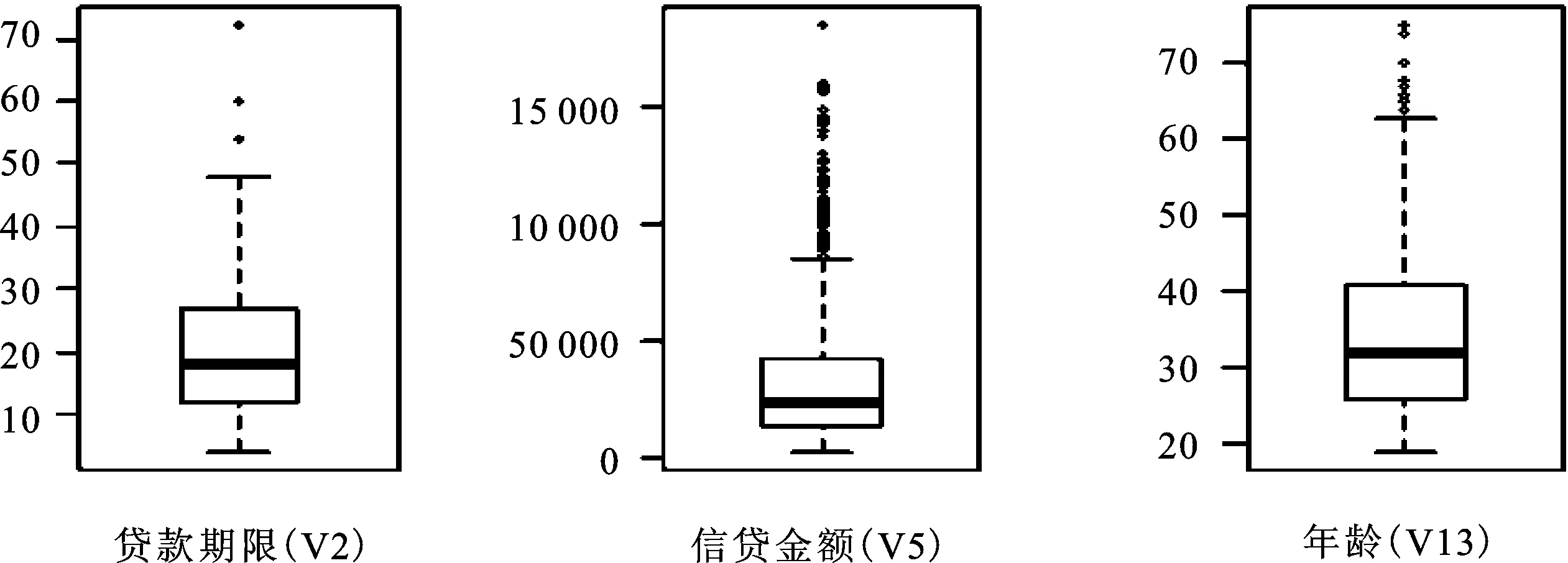
图2 变量V2、V5、V13的箱形图

(二)个人信用影响因素稀疏网络结构关系发现

1.基于multi-logit回归的贝叶斯网稀疏结构学习。贝叶斯网结构学习分为三类：基于约束的结构学习、基于评分的结构学习和混合结构学习。基于multi-logit的贝叶斯网稀疏学习为基于评分方法的扩展，具体实现采用R包discretecdAlgorithm中CD算法。该算法要求水平数为k的变量，对应编码为0，1，…，k-1，故学习结构前需对不符合要求的变量重新编码。CD算法可沿稀疏化算子λ序列生成一系列DAG的最优稀疏估计。由于学习任务具有较高的计算复杂度，默认当DAG估计中边数超过节点数量的3倍时，CD算法终止。基于给定的数据样本、λ下降序列和算法终止条件，本文最终获得8个最优DAG估计。

discretecdAlgorithm包没有提供模型选择的具体实现方法。本文分别尝试BIC(Bayesian Information Criterion)准则、BDe(Bayesian Dirichlet equivalent)得分和对数似然损失作为模型选择标准。论文没有采用交叉验证选择模型，原因在于研究目的不是分类预测而是结构发现。研究发现，对数似然损失不适合作为稀疏模型选择的标准；BIC和BDe得分一定程度上可以实现稀疏模型的选择，但BIC得分更敏感，BDe得分较稳定。表1显示，随着网络边数的增加，测度模型拟合优度的对数似然损失逐渐增大，说明具有较小预测误差的DAG往往趋于拥有较多的边；BIC得分开始缓慢增长，但当边数大于16后，得分急剧降低；BDe得分变化趋势与BIC类似，但没有BIC波动剧烈。

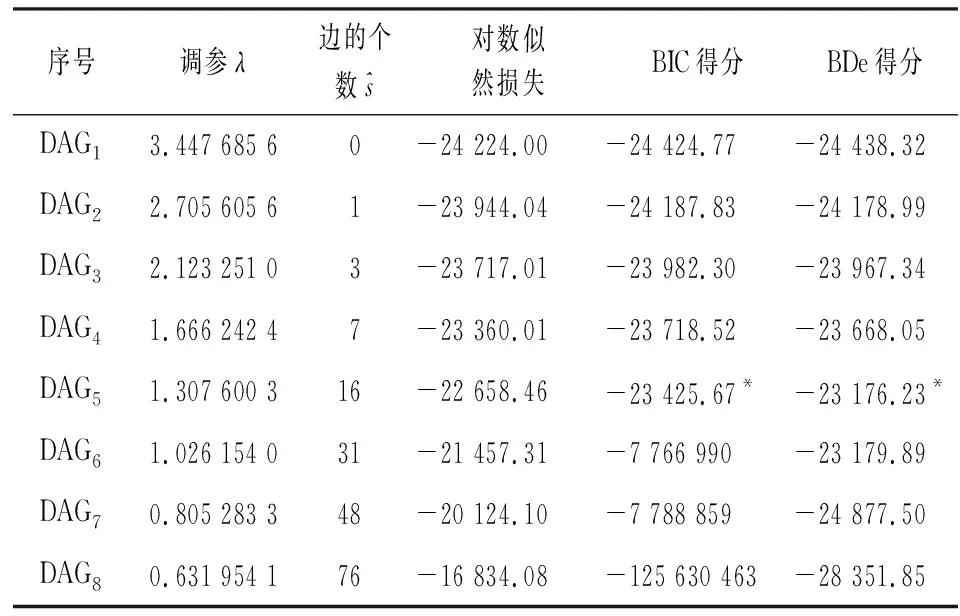
表1 贝叶斯网稀疏结构估计结果相关信息

注：*表示贝叶斯稀疏网络结构得分最大值。

表1显示，DAG5与DAG6二者BDe得分差异非常小，但DAG6对数似然损失值明显较大。所以，下面对边数为16的DAG5和边数为31的DAG6进行比较，检验哪一个为最优模型。图3显示，DAG6包括了DAG5中全部边并新增15条边，其中新增7条指向目标变量V21的边。从图形表示上看，似乎DAG6找到与客户类型相关的更多影响因素和路径。因此，利用R包bnlearn尝试检验数据是否支持这15条边的存在，特别关注每个指向V21的变量是否与变量V21具有直接依赖关系，选择皮尔逊卡方条件独立性检验(表2、表3)，DAG5中每条边检验的P值均小于0.05，说明它们具有较强的概率依赖，而DAG6有12条边P值大于0.05，说明这些边在DAG6中表示的概率依赖程度较弱，其存在性有待商榷。最终从8个DAG估计中选取DAG5作为最优稀疏估计。

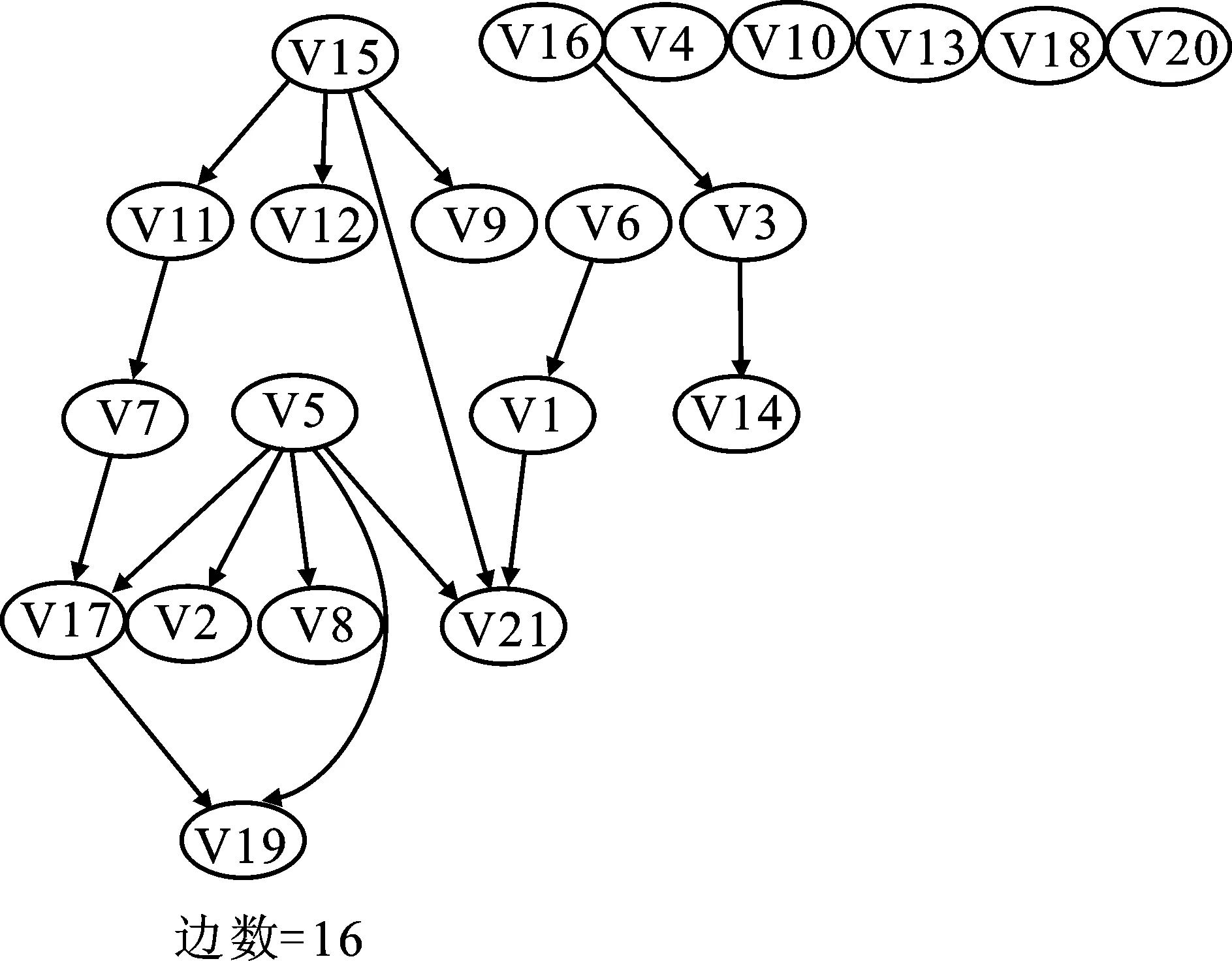
图3 CD算法估计所得的贝叶斯网稀疏结构图(边数=16和边数=31)

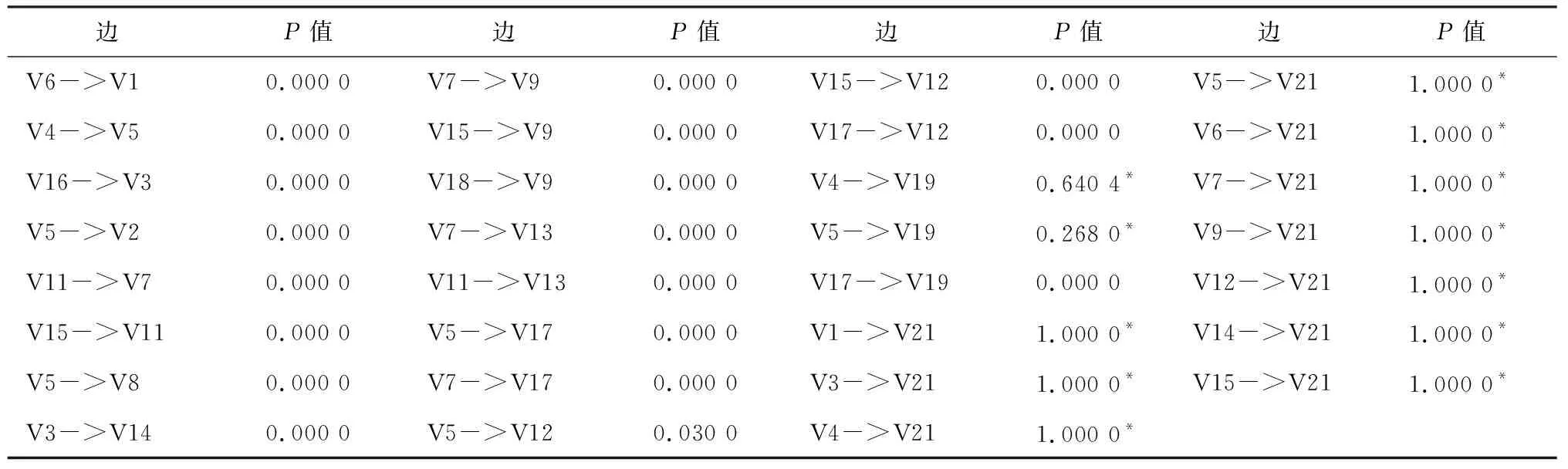
表3 DAG6中每条边条件独立性检验结果

注：*表示对应边的皮尔逊卡方独立性检验P值大于0.05。

2.CD算法与其他算法估计结果比较。利用bnlearn包提供的经典结构学习算法，如基于评分的HC算法、基于约束的GS算法、混合结构学习的MMHC算法，从信用数据学习DAG，所得DAG边数以及BDe得分情况见表4。CD算法中λ大小决定了DAG中边的稀疏性，依据λ序列可以一次生成多个稀疏程度不同的DAG估计，即从最稀疏的空图过渡至较稠密的图；而HC算法、GS算法和MMHC算法基于数据一次只能得到一个DAG估计。表4显示，对于中等规模的网络，HC算法得到的DAG得分最高，CD算法最优结构得分与其非常接近，说明稀疏算法尽管损失了一些信息但仍然能够抓取数据所蕴含的主要信息；而GS算法和MMHC算法，抓取描述数据结构的信息非常少，只有4条或8条边，其DAG对应的BDe得分也相对较小。总体来说，CD算法对于中等规模网络的学习具有一定优势。Fu等对HC算法和CD算法在大规模网络学习中性能进行比较，发现CD算法学习准确率要明显优于HC算法，数据维度越高CD算法越具优越性。

表4 CD算法与经典贝叶斯网结构学习算法估计结果比较

注：*表示从CD算法的一系列最优解中选出的最终稀疏网络结构。

3.结合先验知识改进贝叶斯网稀疏结构。在实际应用中，个人信贷记录与客户类型好坏往往具有相关性，但在DAG5中信贷记录节点V3与客户类型节点V21并不联通。因此，根据先验知识分别测试是否应在DAG5添加边V3->V21或V21->V3。

1)添加边V3->V21。结果显示，新网络BDe得分为-23 233.1，小于DAG5对应的得分。对新网络每条边进行皮尔逊卡方条件独立性检验，发现不仅边V3->V21没有通过检验，并导致边V5->V21、V15->V21也通不过检验，因此排除在DAG5添加边V3->V21。

2)添加边V21->V3。结果显示，新网络BDe得分为-23 157.96，大于DAG5的BDe得分；同时网络中边都通过条件独立性检验，即数据支持在DAG5上新增边V21->V3。

因此，最终的个人信用影响因素稀疏网络结构，见图4，其中节点数有21个，边数为17条，参数个数为214。

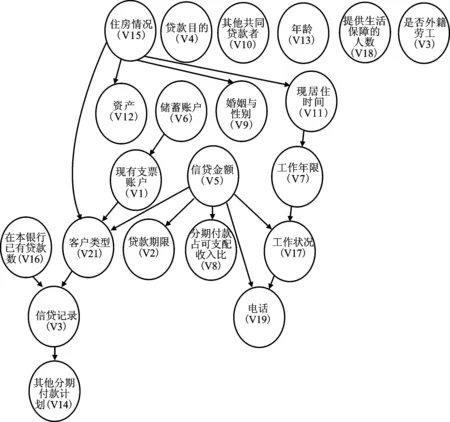
图4 个人信用影响因素最优稀疏网络结构图

4.信用影响因素稀疏网络结构定性分析。图4各节点变量分别表征客户人口特征、工作、经济、贷款等方面的信息，它们与客户类型、信贷记录之间的主要依赖关系被稀疏网络结构抓取并显示出来。影响客户类型的直接因素有：住房情况、现有支票账户和信贷金额。信贷金额的子节点有客户类型、贷款期限、分期付款占可支配收入百分比、电话、工作状况。信贷记录的父节点为在本银行已有的贷款数、客户类型，子节点为其他分期付款计划。贝叶斯网节点间的依赖关系具有传递性，能够捕捉节点间的相关关系，形成彼此连通的路径。例如存在反映客户偿债能力的部分路径：住房情况—>客户类型—>信贷记录—>其他分期付款计划；储蓄账户—>现有支票账户—>客户类型—>信贷记录；住房情况—>现居住时间—>工作年限—>工作状况—>电话。年龄、贷款目的、其他共同贷款者、提供生活保障的人数和是否外籍劳工5个节点被稀疏化为互不联通的独立节点，说明它们对客户类型好坏的影响并不显著。

(三)稀疏网络结构参数学习及贝叶斯网推理

在已知信用影响因素稀疏网络结构的基础上，可以通过参数学习量化节点对其父节点集的概率依赖，并推理分析不同因素对客户类型的影响。参数学习选择贝叶斯估计，因为贝叶斯估计能避免产生稀疏条件概率表，有利于后期贝叶斯推断，它比最大似然估计更稳健，具体采用bnlearn包进行参数估计。已知稀疏网络结构和参数后，利用R包gRain实现基于联合树的贝叶斯网精确推理。贝叶斯网推理可以获得证据已知时事件发生的条件概率，下面根据贝叶斯网推理实验结果，从信贷金额、贷款期限、客户稳定性、客户财务和债务状况方面定量分析它们对信用类型的影响。

1.信贷金额与贷款期限。根据贝叶斯网推理实验结果，研究发现不同等级的信贷规模对客户信用有明显的影响。信贷等级低的客户坏信用发生的可能性下降了2.6%，但随着贷款规模的扩大，违约概率随之攀升，信用风险增大，特别是具有中等信贷规模的客户，其坏信用发生的概率直接由45.8%上升至62%。信贷金额的边缘概率显示，中等信贷规模的客户占全部客户的13.1%，因此银行要特别注意把控信贷额度规模，防控此类客户违约产生的风险。同时，研究发现客户贷款期限的长短对信用好坏影响明显。短期贷款好信用发生的概率略有上升；对于中长期贷款，则坏信用发生的概率明显增大，从45.8%上升到52.3%，故银行应对中长期信贷重点监控。

总之，银行要注意解决业务发展与风险控制之间的矛盾，通过科学的手段与工具合理设定信贷规模阈值，要基于数据挖掘定位银行主要金融产品的类型及期限。同时，银行要进一步加强金融风险意识，尤其是对具有中等信贷规模且贷款期限较长的客户加强防控，设计并实施个性化营销策略，诱导其改变对贷款类型和期限的偏好。

2.信贷客户的稳定性。住房情况一定程度上反映客户的居住稳定性及经济实力，是衡量还款能力和信用风险的重要指标。贝叶斯网推理实验结果显示，住房情况对客户信用的影响较为显著。拥有自主住房的客户，经济实力强，居住稳定，其坏信用发生概率较全体客户下降了3.1%；租房客和公用住房者，经济实力较弱，居住相对不稳定，其坏信用发生可能性明显增高，尤其是共有住房者与整体相比，违约概率上升了7.1%。此外，研究现居住时间对客户类型的影响时，并没有发现客户现居住时间越长其信用越好。

工作年限、工作性质能够衡量客户的工作稳定性。研究发现，工作稳定性对信用好坏的影响并不显著。将信用发生的边缘概率与已知工作年限时信用的条件概率比较，结果并不存在客户工作时间越长，违约概率越小的规律。同样，利用概率推理分析客户工作性质对信用的影响时，发现银行发放贷款的主要对象是技术人员和公务员，占到总体的62.5%，这类人群与全体用户相比信用概率值不变；高级管理人员或个体经营者，占到总体的15.5%，其违约概率相比于总体明显增大，因此银行应对这类人群进一步细化，对工作不稳定的高收入客户提高风险防范，对工作稳定的高收入客户做好客户关系维护，提供产品个性化推荐和服务。

3.信贷客户财务状况。研究发现，财务状况对客户信用影响较为明显。信用评估稀疏结构中，现有支票账户对客户类型好坏具有直接影响，储蓄账户和资产具有间接影响。

现有支票账户和储蓄账户可理解为客户的现金资产。贝叶斯网推理实验结果显示，如果现有支票账户出现透支，则发生坏信用的可能性直接上涨19.5%，如果账户现金大于某个阈值或已签订至少一年的薪水合同，则表明客户具有良好的财务状况，偿债能力较强，此时坏信用发生概率明显降低，由45.8%降至33.5%，因此银行需重点关注账户为负的客户产生的信用风险。同理，分析储蓄账户对客户类型的影响，发现只有当储蓄账户资产规模较低时，坏信用发生概率会增大。不动产、社会保险、汽车和其他类资产对个人信用影响程度相当，具有轻微的正向作用，但对于资产状况未知或没有资产的信贷客户，银行应谨慎放贷，其坏信用发生的概率显著增大。

4.信贷客户个人债务。客户在本银行已有贷款项目数可反映个人债务状况，图4贝叶斯网稀疏结构显示，在本银行已有贷款项目数对客户类型好坏没有直接影响。但是，贝叶斯网推理实验结果显示出更多的细节信息，当好/坏客户个人债务情况相同时，坏客户的还款能力要弱于好客户的还款能力，即坏客户逾期还款的概率更大；当已有贷款项目数超过某一阈值时，好客户还款记录明显优于坏客户，好客户过去逾期还款的概率仅为4.8%，而坏客户高达29.4%；反之，当客户个人债务减轻，贷款项目数低于此阈值时，好、坏客户过去逾期还款概率相差不大。

五、结论

随着大数据征信的发展，传统贝叶斯网表征信用变量复杂网络结构和概率关系时遇到了挑战。基于multi-logit回归的离散贝叶斯网稀疏结构方法作为传统基于得分的结构学习方法的扩展，能够大量减少网络参数个数，降低学习复杂度，提高模型解释能力。

首先，本文首次将基于multi-logit的贝叶斯网稀疏结构方法用于个人信用影响因素结构关系的挖掘，简化网络结构的同时抓取了信用变量间主要关系。然后，离散贝叶斯网稀疏学习最终得到目标问题的一个解路径，基于挖掘信用变量蕴含的主要结构关系的研究主旨，本文分别测试了对数似然损失、BIC和BDe得分在稀疏模型选择中的表现，研究发现对数似然损失不适用于稀疏模型的选择，而BIC得分和BDe得分可用作稀疏模型的选择标准，BDe得分较BIC得分表现更平稳。其次，本文还将该稀疏网络结构学习的CD算法与经典贝叶斯网络学习算法进行比较，发现随着数据维度的增加，CD算法的准确性较HC算法的准确性逐步上升，即基于multi-logit的贝叶斯网络稀疏学习能够得到较好的稀疏网络，在高维环境下经济问题的研究具有一定的适用性。最后，在确定信用影响因素的稀疏网络结构并估计了网络参数后，本文基于联合树进行贝叶斯网推理，量化分析信贷金额、贷款期限、客户居住和工作的稳定性、客户财务状况、客户债务对其信用类型的影响。银行可根据推理结果，发现信用风险大的潜在客户，有针对性地制定各种信用风险防控措施，降低银行资金风险，并且银行可以根据网络结构定性和量化分析结果，制定精准营销策略，引导和激励客户好信用行为的发生，制定惩罚措施避免坏信用的发生。