蒙特卡洛特征样本采样方法研究

刘雪晨，李宝瑜，张 晰

(山西财经大学 统计学院，山西 太原 030006)

一、引言

一个随机变量样本，可以来自实际调查或观察，也可以来自计算机模拟；蒙特卡洛随机样本就是由计算机采样生成的样本。蒙特卡洛方法自二战时期美国物理学家Metropolis提出来以后，在全世界不同学科和专业领域都得到了广泛的应用。由于涉及到随机序列的反复采样，蒙特卡洛方法以高容量和高速度的计算机为前提条件，以统计量的概率分布为核心。在大数据时代机器学习和人工智能技术的发展中，很多知识需要通过对大量数据的模拟和训练来获得，如人工神经网络、支持向量机、随机森林等方法中，都要进行大量数据训练和模拟从而探索最优化结果，因而蒙特卡洛模拟方法也越来越受到重视。

蒙特卡洛方法应用的基础是对随机变量的采样，即样本生成。目前主要有四种对一维变量蒙特卡洛样本采样方法：直接采样法、逆分布函数法、接受拒绝采样法、重要性采样法。

(1)直接采样法，就是按照某种标准的概率分布p(x)直接抽取样本，这是最简单的一种方法。

(2)逆分布函数法(反函数法)，适用于能够求解反函数的有限空间分布的采样。它是先产生均匀分布上的一组随机数，然后作为y带入逆分布函数，得到一组x，这组x就是符合分布p(x)的随机变量样本。

(3)接受拒绝采样法(Acceptance-Rejection Sampling，ARS)。该方法适用于服从非常见概率分布p(x)采样，即首先设定一个方便采样的常用概率分布函数q(x)，如正态分布，以及一个常量k，使得p(x)总在kq(x)的下方；然后采样得到q(x)的一个样本X1，对于这个样本是否被接受为p(x)的样本，就要再从均匀分布(0,kq(x1))中采样得到一个值u。如果u≤p(x1)/kq(x1)，则接受这个样本x1，否则拒绝这次采样。q(x)与p(x)越近似，接受率越高。重复以上过程得到n个接受的样本x1，x2,…,xn。

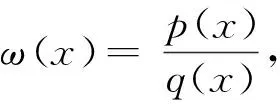
当变量来自高维分布时，无法直接产生独立随机样本，这时需要借助马尔科夫链实现对复杂或高维分布的采样，这就是MCMC(Markov Chain Monte Carlo)采样。MCMC包括Metropolis-Hastings方法和Gibbs方法。MCMC方法最早由Metropolis(1954)给出，他是在研究物理学中粒子系统的平稳性质时想到的，后来Metropolis的算法由Hastings进行改进，合称为M-H算法。M-H算法是MCMC的基础方法，由M-H算法演化出了许多新的采样方法，包括目前在MCMC中最常用的Gibbs采样也可以看作是M-H算法的一个特例。

近些年来，很多学者对上述经典的采样方法进行了完善和补充，研究领域主要集中于高维数据采样。如Andrieu等在2010年提出了粒子滤波MCMC方法(PMCMC)，将一种基于粒子滤波器输出的似然估计方法用于MCMC[2]，Pitt等进一步发展了该方法[3-4]。为了解决多维变量MCMC采样的收敛速度慢的问题，Fu等提出了Fu-Wang法[5-6]，Wang等提出了Wang-Lee算法[7]，这两种算法都是基于多维样本空间随机离散化概念的蒙特卡洛模拟方法。此外，还有顺序蒙特卡洛方法(SMC)，解决多维变量非线性状态空间分布问题，代表性的研究者有Doucet、Andrieu等[8-9]。

目前有关蒙特卡洛采样方法文献的特点，一是理论研究多，数学推导多，可操作性较弱；二是研究多维分布的采样方法多，研究一维变量采样方法的少，对单变量采样方法重视不够；三是对样本的分类和方法的分类缺乏系统性和规范性，还没有形成较完整的方法体系；四是很多研究文献对于采样的目的、样本适用对象、采样需要具备的条件、样本的具体形式等问题模糊不清，例如很多文献对于重要性采样方法的介绍不是讨论其样本如何采集问题，而是讨论如何积分。

一维变量的随机采样方法是蒙特卡洛方法的基础，也是实践中最常用的方法。单变量的随机样本可以用于建模、参数估计、积分计算、机器学习中的模拟训练等很多研究中。本文拟对一维变量的随机采样方法进行系统性研究，在特征样本概念基础上，提出一套较为完整、程序简化、具有可操作性的采样方法，最后用一个回归实例来说明其应用。

二、概念和分类

(一)特征样本概念

特征样本的概念由李宝瑜等人于2016年提出[10]。特征样本是在变量特定的值域范围内按照变量的分布特征采用机器采样的方法生成的随机样本，这种样本在各种模拟计算中更能反映变量之间的关系。如果每个变量都能够采用其特征样本，对变量的代表性就会更好一点。每个特征样本都具有给定的特征和样本量。蒙特卡洛模拟条件下，面对复杂的样本要求，应该研究一套完整的特征样本采样方法。

变量的特征首先是分布特征，分布特征一般都可以用通用的数学解析式表达：

y=f(x)

在这个函数关系中，或者是把y当作是x的特征，或者是把x当作y的特征。把变量特征简单地看作概率特征是不全面的。特征样本的特征包含概率特征但不限于概率特征，f(x)既可以是概率密度函数也可以是一般数学解析式。已有的蒙特卡洛的采样方法通常只是产生概率分布的特征样本。

特征样本是根据随机变量的某些特征，用机器采样方法生成的伪随机样本。特征样本的一般形式可以表达为：

ζ(x,y)=n,y=f(x),ζ[a,b]

特征样本采样中首先需要引入目标变量和标识变量两个概念。目标变量是将要对其抽取样本的变量，是期望生成的样本，可以是y，也可以是x；标识变量是用来辅助生成目标变量的随机变量，如果目标变量是y，标识变量就是x；如果目标变量是x，标识变量就是y。ζ表示目标变量的特征样本。从表达式可以看出，一个特征样本包含三个特征，一是样本大小n，二是用函数式表示的分布特征，三是目标变量的值域ζ[a,b] 。

特征样本是随机样本，可以重复采样，这就意味着每次采样获得的样本是不同的。由于按分布特征采样，所以样本的特征部分是稳定的。

(二)特征样本的分类

本文对特征样本做如下主要分类：

1.分布型样本和曲线型样本。分布型样本是服从某种概率或非概率分布的特征样本。它以y=f(x)中的x作为目标变量，以x的密度函数或非标准函数y作为标识变量。曲线型样本与分布型样本相反，其目标变量是y，标识变量是x。

2.频率分布样本和值域分布样本。分布型样本可以分为两类，一类是样本中体现了x出现的频率，一个x值可以多次出现在样本中，出现的次数由标识变量y决定，例如正态分布的x样本可以在均值附近出现多次，这类样本可以称为频率分布型样本；另一类样本是x值唯一对应于某一个y值，同一个x值在一个样本中只出现一次，这类样本可以称为值域分布样本。现有的蒙特卡洛采样方法多数都是讨论频率分布样本而忽略值域分布样本。现实中如果在函数运算中与y的样本量一一对应，用的较多的是值域分布样本。频率分布样本自身看起来是完美的，但在构建另一个统计量时则难以与y函数对应起来。

3.有序样本和无序样本。无论是以y或是以x作为目标变量，都涉及到一个样本的有序性问题。频率分布型的样本是无序的，值域分布型样本一般是有序的。如果以y作为目标变量、x作为标识变量，在函数式统计计算中一般要求x是有序的，只有x有序，才能与y对应。截面数据一般是分布型，也是无序样本；时间序列样本，可以是分布型也可以是曲线型。在曲线型样本情况下，x作为标识变量，可以是一个实质性变量，也可以是时间t，如果是t，则要求样本是有序的。

4.标准分布型样本和非标准分布型样本。标准分布型样本服从标准的概率分布。如均匀分布、正态分布、贝塔分布等，其分布特征体现在样本自身包含了其频率特征，在每一值点处都有不同的频数出现，既属于频率分布样本，也属于无序样本。

非标准分布型样本是以非标准密度函数y=f(x)中的y为标识变量，以x作为目标变量，此时的x样本是值域分布型样本，也是有序样本。

非标准分布型可以进一步分为已知函数式和未知函数式样本。已知函数式的样本按照是否能求出反函数又可以分为两类样本；未知函数式的样本则需要特定的方法采样。

5.标准曲线型和非标准曲线型样本。标准曲线型样本是有标准(常见)密度函数支撑的曲线，目标变量为密度函数值y，标识变量为x，根据变量y的形态特征，选取曲线形状相似的标准密度函数作为其函数表达式，目标样本值就是密度值。如果目标变量值大于或小于密度值，可以通过一定的方法换算为实际值。

非标准曲线型样本。很多曲线型变量与其标识变量的函数式无法用标准密度函数表示，这类变量划分为非标准曲线型。它的目标变量y与标识变量x之间具有一般数学函数关系，并可以根据是否具有明确的函数式分为两类：已知函数式和未知函数式(但已知一组函数值观察样本)。已知函数式也可以进一步分为容易求解反函数和不容易求解反函数两类样本，二者采用的采样方法也不同。

6.解析型样本和模拟样本。解析型样本是已知y=f(x)函数关系，给定x或y的一些特征，获得x或y的样本。有时我们无法知道这种函数关系，得不到x或y的解析式，而只能得到一组实际观察值，此时蒙特卡洛模拟需要在这一个观察样本基础上生成随机样本，即生成模拟样本。

(三)特征样本采样的思想

第一，特征样本是基于经验生成的随机变量样本，是对现实变量的模拟。每个特征样本一定要尽量符合变量的实际情况，而要能够给出符合实际的变量特征，就需要依靠人的先验经验。将人的经验纳入样本采样过程，如果经验判断是正确的，对样本的模拟就会更加符合实际或接近实际。一个变量在一个特定的取值区间，是属于分布型样本，还是曲线型样本？时间序列样本是递增还是递减？这需要有经验支持，也决定了目标变量的类型。当然，如果所依赖的经验是错误的，就可能使得样本偏离实际。将人的经验纳入特征样本的生成，符合贝叶斯统计思想。

第二，特征样本是在特定取值区间的样本。有些变量的取值区间可能需要表达为正无穷或负无穷，如正态分布，但在标准正态分布下实际起作用的区间一般不超过6个标准差，所以原则上每个特征样本都必须给出一个有限值域。

第三，特征样本是可以重复抽取的样本，而且每次采样的结果都要在符合分布特征前提下具有随机性，这是因为在蒙特卡洛等应用中需要对统计量进行多次重复来模拟。每次模拟都需要不同的随机样本，当我们给定变量的分布特征和值域以后，就能够在重复采样条件下生成具有相同特征的多个特征样本。

第四，给定变量的分布特征可以有两种方法，一种方法是直接依靠经验确定，另一种方法是通过对实际数据的观察来确定。确定变量的值域范围也可以是同样的方法。

第五，如果我们要对某个变量进行研究，利用其构建统计量等，就需要了解其分布特征和值域。如果对变量一无所知，对变量的走势形态、最大最小值等基本信息都不了解，所做的工作就可能因不符合实际而成为无实际意义的数字游戏；如果采样者缺乏经验，可以通过观察实际数据确定分布特征和值域，做到这一点应该不会有很大困难；如果将一个实际数据的观察样本看作一个样本特例，在一个区间内按照变量特征重复采样产生多个随机特征样本，则包括了各种可能的样本，其代表性可能会更强。

三、特征样本采样方法

特征样本的生成方法从总体上来看，就是利用已有的某种计算机语言内部的随机数生成函数生成需要的伪随机数样本。在现有的一维变量4种采样方法基础上，本文又提出了一些新的方法，经过归纳提炼，分为10种具体方法。

(一)分布型样本采样方法

1.标准分布法。属于现有的4种采样法之一的直接采样法，用于生成标准分布型样本。给定标准分布要求的参数，利用计算机函数直接生成x的频率分布样本。例如，用R函数x=rnorm(n,μ,σ)可以直接生成均值为μ，标准差为σ的正态分布样本，x=runif(n,a,b)可以生成区间为[a,b] 的均匀分布样本、x=rbeta(n,α,β)可以生成参数为α和β的偏态分布(贝塔分布)样本等。

2.反函数分布法。属于目前常用的逆分布法，可用于已知函数式且能够求出反函数的非标准分布型样本。逆分布法是从y采样，然后带入反函数式得到x样本，但这样采样得到的是x频率样本，同时也可以对其进行改进，从x采样，得到x的值域样本。方法是先给出ymin(y),max(y)，将y的最小最大值带入反函数式，求出x的值域，然后直接在x值域中按均匀分布生成x的随机样本。如果y=f(x)是单调减函数，就需要把x的最小最大值互换。

3.比例分布法。这是本文设计的一种方法，适用于已知函数式但难以求解反函数的非标准分布型样本，是与现有的接受拒绝采样和重要性采样法相似但有所改进的一种方法。比例分布法要求有一个已知函数y=f(x)，且给出x在定义域内的一个任意值域xmin(x),max(x)，升序排序之后，正方向带入函数式生成一组y，在y的每一值点处计算一个与x对应的比例k，然后在y的每一值点处给定一个随机变动小区间(幅度大小自由设定，它决定了随机范围)，利用均匀分布在该区间生成1个随机数，然后利用反函数和k生成x的值域分布型样本。其方法和步骤为：

(1)在x值域范围按均匀分布采样得到x初始值并排序。

(2)将x初始值带入函数式得到一组y初始值。

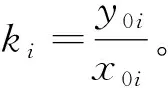
(4)确定一个随机性范围，在每个y值点处的小区域按均匀分布随机生成一个随机数y1i。

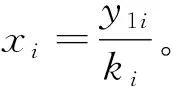
这样生成的样本服从y=kx的分布等价于原y=f(x)，得到的x样本是在y的一定值域内的样本。该方法的思想是将复杂的分布简化为一个简单分布y=kx，从而能够按照简单分布生成样本。对于x值域的确定，需要尽量接近实际问题的意义。

4.分区频率分布法。这是本文设计的另一种采样方法，适用于生成有函数关系y=f(x)，但未知具体解析式的x频率样本，这种情况一般是已知y的一组观察样本点，寻找到一组x的样本点，使得x的样本服从y=f(x)分布，因而一旦给出一组随机数x，就能使其服从该特定分布。

分区频率分布法的思想是：在y为数值变量的情况下，y值可以换算为密度值。根据以下方法和步骤，可以得到一个x频率分布随机样本。

(1)设定一个x区间xmin(x),max(x)，将其离散化为与y对应的n个观察点。

(2)将y的观察值换算为频率值。如果有负数，需要将序列等比例变为正数。频率换算公式为。

(3)设定x的样本容量N，N=kn，k是y的样本容量的倍数，需要足够大。

(4)计算每个x观察点需要分配的样本数，Ni=yidN。

(5)按均匀分布在每个x观察点抽取Ni个xi，合并得到的x即是服从y=f(x)分布的样本。

5.分区值域分布法。这也是本文在比例法基础上设计的另一种简便采样方法，适用于在已有y的观察样本的情况下，生成x的值域样本，即要求生成与y值一一对应的x值点，且服从y=f(x)分布。这里不需要进行y的频率转换，但需要对y分区以后直接采用比例法。其步骤为：

(1)设定一个x区间xmin(x),max(x)，将其离散化为与y对应的n个观察点。

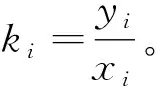
(3)对每一个yi给出一个随机波动区间，按均匀分布在此区间采样。

(二)曲线型样本采样方法

1.标准曲线法。用于生成服从标准分布的曲线型样本。其目标变量是ymin(y),max(y)，标识变量是x，y与x的函数式是y=f(x)。这种方法的思路是先在标准分布的有限值域范围内生成密度函数值yd，然后通过一个转换算子将其转换为y的样本值。转换算子表达式为：

y=min(y)+(max(y)-min(y))×

由于现有的计算机程序语言都只有标准分布的采样函数，得到的结果都是密度函数值，而标准曲线要求的是实际数据值。上式就是一个非常有用的转换算子，可以通过转换算子将任何一个值域的序列转换为分布不变的特定最小最大值的序列，同时也适用于密度函数值转换为实际数据值。

例如，要生成一个递减指数曲线，在R语言中先用命令dexp(n,λ)生成一个密度函数曲线，再用以上公式换算成实际值曲线。如果要得到一个递增指数曲线，则可以通过变换正负号实现。

2.非标准曲线法。适用于不具有标准概率分布但具有一般数学解析式且无法求出反函数的y曲线样本。首先确定一个x的初始值域，按均匀分布采样排序后直接带入y=f(x)得到y的初始值y0，然后再根据实际要求的y的值域对x值域进行调整，按调整后的x值域重新对y采样，其方法和步骤为：

(1)确定x的一个值域，按均匀分布在计算机上采样并按升序排序，得到x的样本。

(2)将生成的x样本带入函数y=f(x)函数式，得到一组y0样本。

(3)调整变换x值域重新采样，得到y的最终样本。

3.反函数曲线法。适用于已知函数式且能够求解反函数的非标准曲线型y样本。能够求解反函数的解析式一般都是单调函数，所以反函数曲线法是在反函数分布法的基础上，进一步对x按照升序方式来排序，变成有序样本，然后再次正向带入函数式得到y样本，其方法和步骤为：

(1)按给定的y值域利用反函数求得x值域。

(2)按均匀分布在x值域用计算机采样并排序得到x样本。

(3)将x值带入y函数式得到y样本。

4.比例曲线法。当f(x)函数形式复杂且难以求解反函数时，比例曲线法就是在给定y[min(y),max(y)] 的条件下，生成一个服从y=f(x)的曲线样本。为了得到y的随机样本，需要让标识变量x具有随机性。所以，首先要在一个值域范围(尽量接近实际)任意给出一个x0的均匀分布样本，排序之后正向带入f(x)得到一组y0。此时，就可以算出y与x在各个值点上的比例k。当再次在x值域生成随机数后，带入y=kx即可得到y的随机样本，其方法和步骤步骤为：

(1)给出一个x的值域按均匀分布采样并排序得到x0样本。

(2)将x0i带入函数式求得一组y0i值，如果y0i的值超过其值域，则重新确定x值域对x0进行采样。

(3)计算一组比例：ki=y0i/x0i。

(4)再次按均匀分布在x值域随机采样并排序得到x1i。

(5)将x1i带入公式y1i=kix1i，得到y的曲线样本。

这一种算法除了能得到y的随机样本外，还能得到一个简化后的解析式y=kx。

5.自助曲线法。在已有y的观察样本的情况下，如果要使其具有随机性，相当于在样本中再采样。具体方法是在y的每个值点附近随机采样，生成与原样本相比特征不变而具有随机性的样本。

Bootstrap方法是常用的生成再生样本的方法，但一般Bootstrap方法只能生成无序样本，而曲线样本要求是有序样本。

表1中列出了上述10种方法以及它们的特征和关系。

(三)频率分布样本与值域分布样本的变换

利用反函数分布法、比例分布法和分区值域分布法生成的特征样本，不能以样本观察值自身的频数来反映其分布特征，而是x与y点对点的值域样本。值域分布样本与频率分布样本是可以互相转换的。从值域样本转换为频率分布样本的方法是先将y序列变换为频率序列，然后在x的每一值点处按给定的样本容量及频率重复采样，合并以后的样本就是值域分布样本转换后的频率分布样本，其方法和步骤为：

(1)给定大于原样本容量n的一个分布样本容量N。

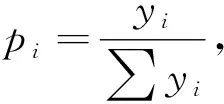
(3)按pi将N分配到对应的xi值点处，计算每个xi在样本中的频数。

(4)在每个xi处重复生成piN次样本。

(5)将重新采样后的xi合并，得到x的频率分布样本。

对于频率分布样本向值域分布样本转化，只要将x排序之后分区，取其每个区的均值即可。

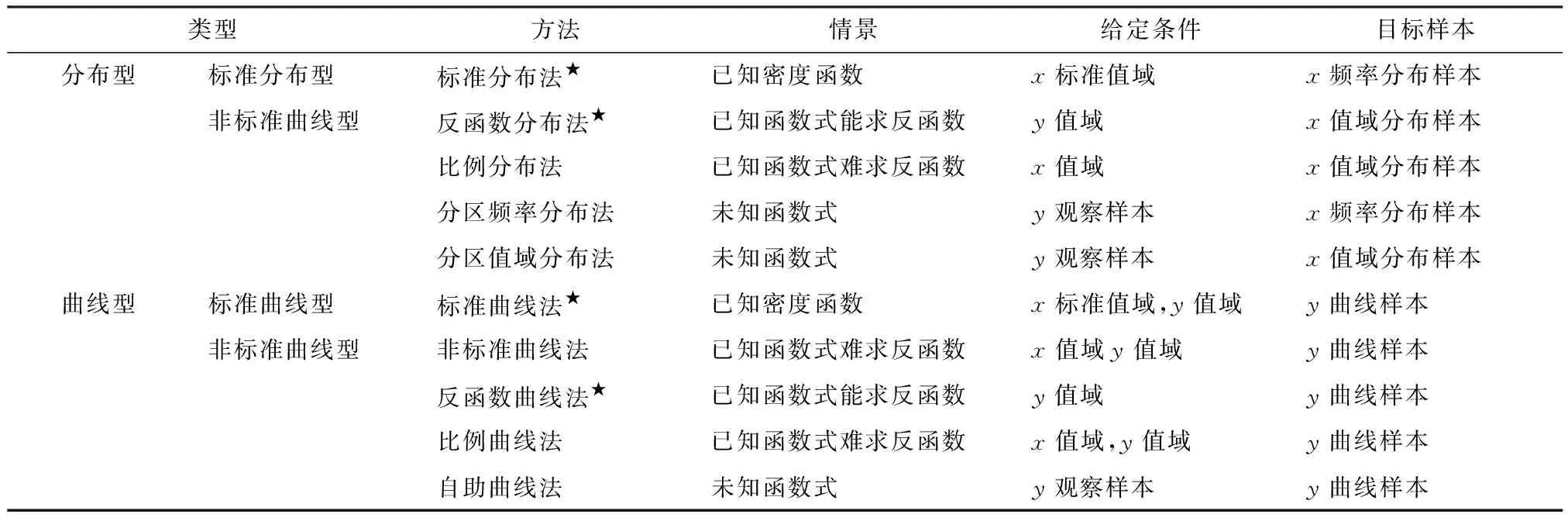
表1 特征样本采样方法

注：表中带★号的4种方法是现有的方法，其余的方法是本文提出或改进的方法。

四、采样方法应用实例与比较

下面列举几个例子来说明上述采样方法的应用，程序用R语言给出。

(一)采样实例

例1：比例分布法

用于生成已知函数式但难以求出反函数的x值域分布样本。已知目标变量x的函数为y=x-x2+ex，给出x的值域为[0，5] ，要求的样本量为30。设定区域随机区间为5%，可以利用以下程序生成值域分布样本。

n=30

x0=matrix(,n,1)

y0=matrix(,n,1)

x0[,1] =sort(runif(n,0,5))

y0[,1] =x0-x0^2+exp(x0)

k=matrix(,n,1)

k[,1] =y0/x0

y=matrix(,n,1)

x=matrix(,n,1)

i=1

while (i<=n){

if(y0[i,1] >=0){

y[i,1] =runif(1,y0[i,1] *0.95,y0[i,1] *1.05)}else{

y[i,1] =runif(1,y0[i,1] *1.05,y0[i,1] *0.95)}

x[i,1] =y[i,1] /k[i,1]

i=i+1}

plot(x,y) #图1

本次采样生成的样本为：

x=(0.01,0.66,0.75,0.76,0.94,1.38,1.53,2.00,2.15,2.05,2.16,2.29,2.17,2.57,2.55,2.64,3.01,3.01,3.09,3.49,3.6,3.40,3.95,4.11,4.21,4.57,4.52,4.84,4.91,4.88)

y=(1.00,2.16,2.27,2.27,2.61,3.46,3.83,5.25，5.99，5.84,6.19,6.73,6.45,8.83,9.50,10.40,13.18,14.00,15.18,23.01,25.11,25.09,43.38,51.48,64.07,76.02,81.16,90.92,97.07,119.87)

例2：分区频率分布法

已知一组容量为10的观察值y=(55,131,44,12,22,33,100,-16,95,142)，x的值域为[100,150] ，要求的样本容量为200。x的随机波动幅度在5%之内。希望在x值域内生成x的频率分布样本，可以利用以下程序实现：

n=10

N=200

y0=as.matrix(c(55,131,44,12,22,33,100,-16,95,142),n,1)

if(min(y0)<=0){

y=y0+abs(min(y0))+1}

by=as.matrix((y/sum(y)),n,1)

minx0=100

maxx0=150

xd=(maxx0-minx0)/(n-1)

x0=matrix(0,n,2)

i=1

while(i<=n){

x0[i,1] =minx0+(i-1)*xd

if(round(by[i,1] *N)>=1){

x0[i，2] =round(by[i,1] *N)}else{

x0[i,2] =1}

i=i+1}

nn=max(x0[,2] )

i=1

while(i<=n){

if(x0[i,1] >=0){

cc=runif(x0[i,2] ,x0[i,1] *0.95,x0[i，1] *1.05)}else{

cc=runif(x0[i,2] ,x0[i ,1] *1.05,x0[i，1] *0.95)}

if (i<=1){

x=as.matrix(cc)}else{

x=rbind(x,as.matrix(cc))}

i=i+1}

hist(x,breaks=50) #图2

例3：反函数曲线法(逆s曲线)

可以利用以下程序实现:

miny=-20

maxy=80

n=200

miny0=0.001

maxy0=0.999

minx=-log(1/miny0-1)

maxx=-log(1/maxy0-1)

x=sort(runif(n,minx,maxx))

y0=1/(1+exp(x))

y=miny+(maxy-miny)*((y0-min(y0))/(max(y0)-min(y0)))

plot(x,y) #图3

例4：非标准曲线法

有一个函数式y=20+15x+3x2，目标变量y的值域确定为[0，120] ，无法求出y的反函数。给出一个x的值域为[-100，100] ，要生成一个样本容量n=200的y的曲线样本。程序为：

n=200

x=sort(runif(n,-100,100))

y0=20+15*x+3*x^2

y=0+(120-0)*(y0-min(y0))/(max(y0)-min(y0))

plot(x,y) #图4

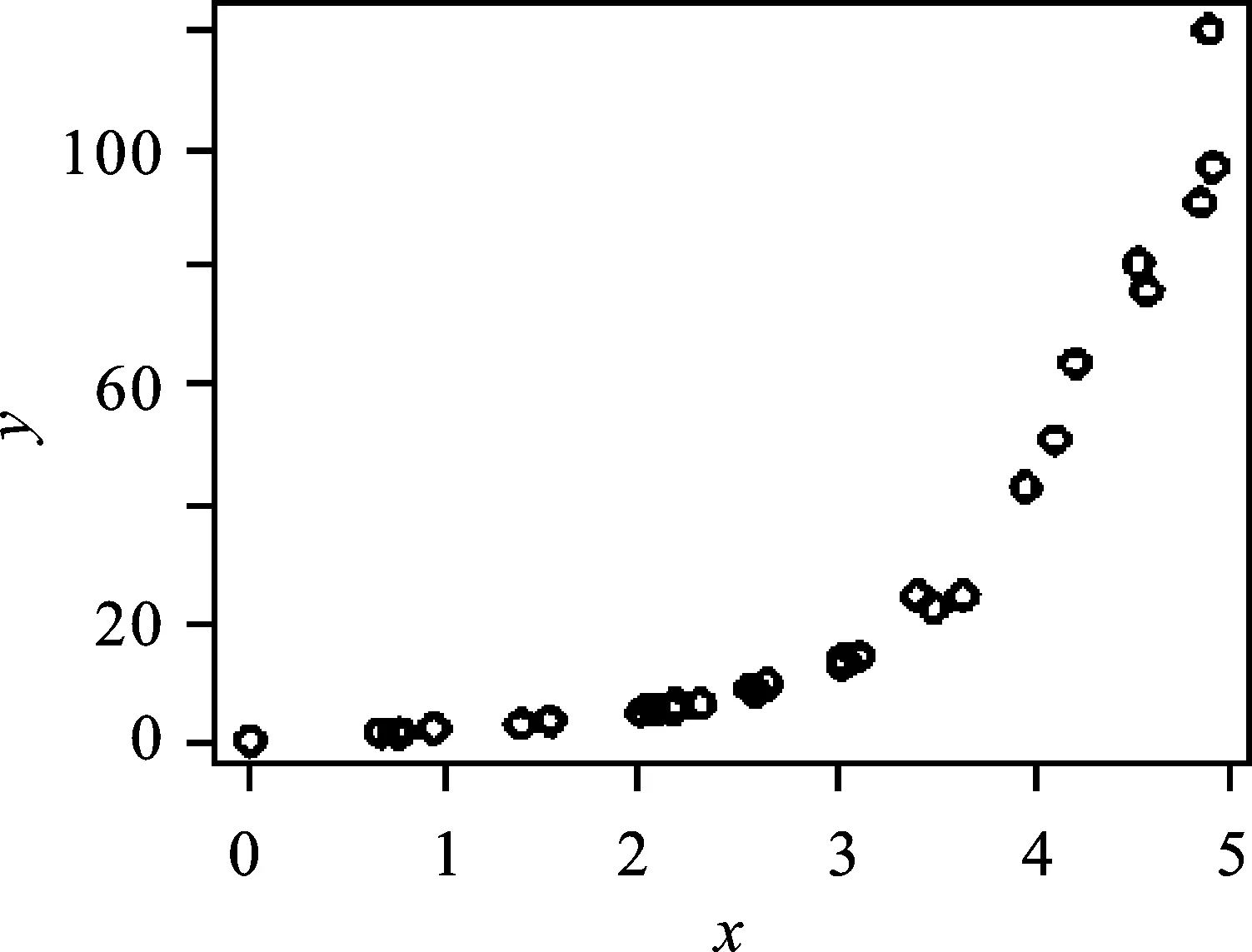
图1 比例分布法样本

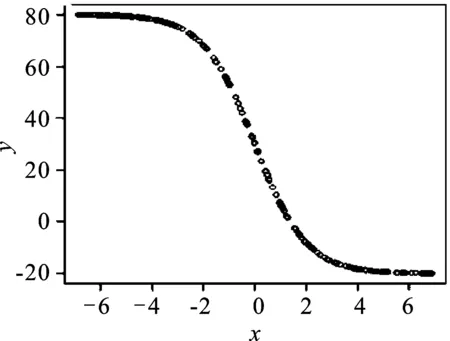
图3 反函数曲线法样本

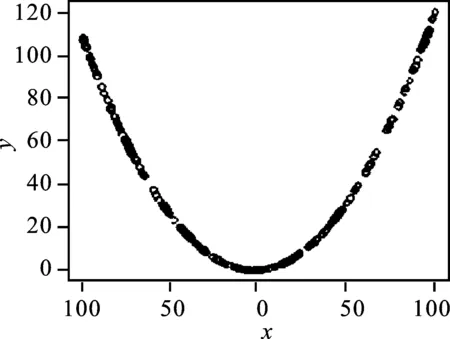
图4 非标准曲线法样本

(二)本文采样方法与现有方法的比较

本文讨论的标准分布法、标准曲线法都属于现有的直接采样法类型。反函数法与现有的逆分布函数法基本相同，但本文区分了分布样本与曲线样本，也给出了规范的算法。本文提出的比例法和分区法与现有的重要性采样法、接受拒绝采样法相比有较大的不同。

重要性采样法和接受拒绝采样法都是由已知表达式的f(x)，生成x的分布样本，其共同点是都需要另外一个近似分布g(x)，都需要计算一个比例c=f(x)/g(x)，且都要有f(x)的具体数值才能进行实际计算。在能够计算c的前提下，两种方法采用了不同的策略选取x的样本点。重要性采样法是把c当作权重，根据权重大小决定x点的样本频数，接受拒绝采样法是把c当作一个衡量是否接受x样本点的标准，样本点如果落入f(x)区域内则接受。

本文提出的比例法，也需要计算一个比例向量k，但不需要从另外的分布计算，而是利用f(x)自身的信息来计算，计算式是k=f(x)/x，免去了这两种方法寻找近似分布的环节，计算也更加简单。

接受拒绝采样和重要性采样的近似分布g(x)的x值域必须覆盖f(x)的x值域，否则c就会变成无穷大或无穷小，把本来属于f(x)的样本点拒绝在外，或接受了本来不属于f(x)的采样点。本文提出的比例法和分区法不受此限制，可以是f(x)定义域内的任何区域。

接受拒绝采样法和重要性采样法不仅要求已知f(x)的函数式，而且要求在每个x点处都有具体函数值，因为如果仅仅是一个表达式而无具体函数值，c是无法计算的，本文的比例法也如此。但是，在缺乏f(x)函数式的情况下只要有一组样本数据，本文提出的分区分布法就很容易地解决了服从f(x)分布的x频率分布样本的生成问题。分区法并不要求必须有f(x)的函数式存在。

现有的各种经典采样方法没有区分频率分布样本和值域分布样本，实际上都只是讨论频率分布样本。本文对两类样本进行了区分，给出了不同的采样方法，并给出了两类样本的互相转换方法，这就为后续应用提供了便利。

现有的方法不重视区分分布样本和曲线样本，本文对两类样本做出了区分，设计了不同的采样方法，并给出了曲线样本通用的值域转换算子，这就为序列之间的值域变换提供了规范的方法。

重要性采样方法一般被认为是设计为计算积分或均值的方法，但这种方法过于繁琐。实际上，只要已知一个函数式，无论其如何不规则、如何复杂，在给定x值域的情况下都可以用一个很简单的分区法得到结果，本文给出一个计算方法和公式：

给定一个函数式f(x)和x值域[a,b] ，指定分区数为n-1，计算c分区后的值点函数：

其中(b-a)/(n-1)是x每个区间的长度。在x值域分布样本中，a与b既是值域区间，也是x的最小最大样本点值，在这种情形下任何积分都可以转化为：

n越大，越收敛于积分值。用这个公式可以很简单地把复杂的积分转化为离散化的求和。

现有文献中对采样方法的讨论，多数都是数学理论推导，对于各种方法在应用中的前提条件、必要步骤、适用条件、采样目标等问题都不够重视。例如在接受拒绝采样中，是仅仅需要一个f(x)解析式还是需要其数值？采样过程是否需要遍历f(x)的所有值点？是否可以限定样本容量？在介绍重要性采样的文献中，很少有人关注x的样本形式、样本容量，样本频率等问题，而重点讨论如何求积分面积或另一个函数的均值问题。本文讨论的各种方法，都具有采集样本的实际可操作性。

五、特征样本在蒙特卡洛多元回归中的应用

为了模拟2016—2017年两个年度24个月中国货币供应量与有关变量的关系，下面例子采用特征样本重复采样回归方法，建立多元回归模型来估计回归参数。

y代表货币供应量，x1代表固定资产投资增速，x2代表工业品出厂价格指数，x3代表出口总额增速。模型形式为：

现在可以采用三种方法估计回归系数：

第一种方法是常规的最小二乘估计法，这种方法完全依赖原始数据样本。

第二种方法是Bootstrap方法，在常规回归结果的基础上，采用残差法进行重复再采样(例如200次)，对模型进行校正。

第三种方法是建立在特征样本基础上的蒙特卡洛回归。这种方法不依赖观察数据，但要根据经验确定各个变量的分布特征和值域。

根据观察和经验，得知各变量的特征，详见表2。

表2 变量特征表(月度数据：2016.1-2017.12)

据此按照各个变量的特征采用前述特征样本随机采样方法，每次对每个变量独立抽取各自的特征样本(n=24)，货币供应量指数采用标准曲线法采样，先用均匀分布在y的值域采样，然后排序，固定资产投资增速和工业品出厂价格指数采用标准曲线法采样后，用转换算子将其转换到实际值，出口增速采用反函数曲线法采样；各个变量采样后，按照有序排列的方法，将3个x变量的样本合并为一个包含4个变量的矩阵(加一个单位列向量)，采用最小二乘估计方法对y进行回归；计算机模拟重复200次，得到200个回归方程及各变量系数，每个变量的200个系数各自形成一个模拟t分布，这里用的原假设为估计参数等于参数均值的设定，与一般的检验方向相反；按照系数出现最大频率即每个系数最接近均值的标准，可以找到一个最优的回归方程及其回归结果。三种方法估计系数在表3中列出。

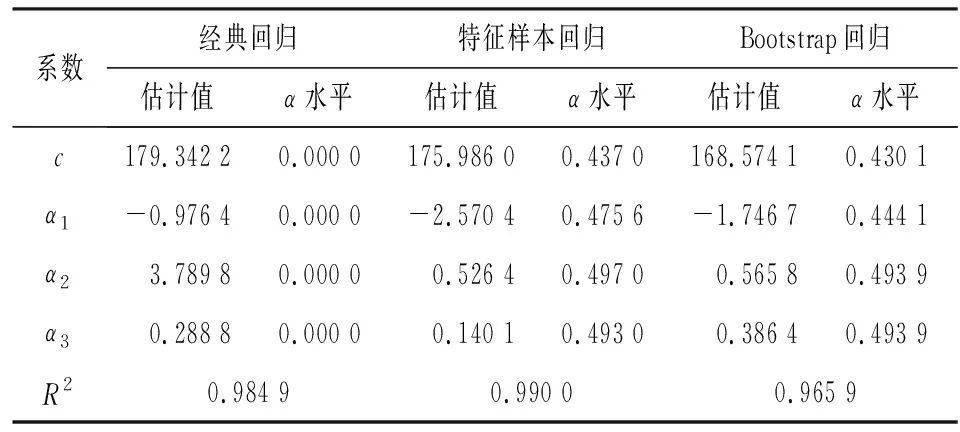
表3 三种方法回归参数估计结果表

三种方法都采用t检验，经典回归的系数是假设性检验，是原假设为0的拒绝性检验，后两种方法由于重复采样估计，已经有了采样分布的均值和标准差，所以是接受性检验，不落入拒绝区域就接受。可以看出，三种方法的回归结果并无很大差别，区别在于经典回归仅是一次性估计，有可能以一次估计的偶然性代替了必然性，后两种方法则可以算出其接受概率(α接近0.5，说明系数接近均值)。Bootstrap回归是在经典回归基础上进行的，增加了步骤但并没有增加样本信息。特征样本回归则是在没有利用样本具体数据，只是了解其分布特征条件下做出的估计，很明显具有其特定的优势，而且是在多样本条件下利用大概率标准做出的选择，符合统计学原理。在数据不完整甚至无观察样本数据的情况下，只要对变量特征有所把握，就能估计出来一个不错的结果。

六、研究结论

本文的整体性贡献主要有：对特征样本的概念进行了界定，提出了特征样本采样的思想，对特征样本进行了系统分类；对特征样本采样方法进行了系统性研究，整理和设计了特征样本采样的10种方法，给出了每种方法的适用类型和所要求的计算条件；在方法设计中，特别侧重于实践可操作性。每种方法都给出了比较规范的公式和步骤。

本文的具体创新有：

第一，区分了分布型样本和曲线型样本，进而将分布型样本划分为频率分布样本和值域分布样本。设计了比例分布法用于生成值域分布样本，给出了值域分布样本与频率分布样本的转换方法，并将该方法用于曲线样本。本文的比例分布法与重要性采样法和接受拒绝采样法都采用了某种比例，后两种方法可以看作是比例分布法的一种类型，但本文的比例分布法不需要另外的分布，而是将一个复杂的函数化简为一个简单的函数y=kx，更加简便易行，这也是本文没有将这两种方法纳入特征样本采样方法体系的原因。

第二，设计了分区分布法，用于生成频率分布样本和值域分布样本。在缺乏函数解析式的条件下，为特征样本采样提供了另外一种新的思路。

第三，给出了值域分布样本向频率分布样本转换的公式，便于在不同条件下生成的样本都能在后续应用中按需要选择。

第四，给出了通用的曲线样本的转换算子,使得按标准和非标准曲线生成的初始样本能够很方便地转换为目标值样本。

第五，给出了a，b值既作为x区间最小最大值，也同时作为x样本点值条件下求积分面积的近似公式，它与通常教材中给出的a，b值仅仅作为区间值的公式略有不同。利用它不仅可以计算复杂函数式的积分，也可以在任何一点按区间计算x≤xi时的面积或概率。

本文的基础性意义在于，样本的生成是构建一切统计量、进行统计推断、统计模拟、统计检验的基础。大数据时代，一些传统的抽样调查将被计算机模拟采样所替代。在机器学习和人工智能中，很多过程中都需要蒙特卡洛模拟。目前蒙特卡洛采样方法的研究还缺乏系统性、规范性和可操作性。本文对特征样本采样方法的系统性研究，将有助于蒙特卡洛方法的应用更加完善。