大额索赔条件下的车险费率厘定

张连增，王 缔

(南开大学 a.金融学院；b.中国特色社会主义经济建设协同创新中心，天津 300350)

一、引言

车险费率厘定是财险公司设计产品的核心内容之一。20世纪早期，费率厘定大多采取单因素分析法和最小偏差法。自20世纪90年代中期始，随着数据收集工作、统计分析方法和计算机技术的不断发展，广义线性模型(GLM)开始成为广泛应用的费率厘定工具。

1972年，广义线性模型(GLM)最早由Nelder和Wedderburn提出，并在国内和国外获得了较快发展和广泛应用。在国外研究中，McCullagh和Nelder首次对广义线性模型进行了全面的总结，并将其应用于车损险数据的分析[1] 21-47。Yip和Yau针对车险数据中存在的过度分散和索赔次数存在的零膨胀现象，提出可以应用零膨胀泊松模型(ZIP)和零膨胀负二项模型(ZIBN)进行分析，此外，也可以应用hurdle模型[2]。Jong和 Heller应用GLM对车险频率和强度数据分别进行分析，并提出了该方法的优点[3] 64-80。在国内研究中，卢志义、刘乐平提出如果使用广义线性模型厘定车险费率，一般需从索赔频率和索赔强度两个方面分别建立模型，但广义线性模型面临的一个重要问题是对模型的有效性诊断[4]。孟生旺、徐昕探讨了索赔频率的预测模型及其应用，认为当实际索赔频率数据存在过度离散特征时，采用一般的泊松回归模型会使费率厘定缺乏可靠性，此时可以采用负二项回归模型、泊松逆高斯回归模型等[5]。

在传统的纯保费预测模型中，通常对索赔频率和索赔强度分别进行预测，然后将两者相乘即得到纯保费的预测值。其中预测索赔频率最常用的模型是泊松模型，预测索赔强度的常用模型是伽玛分布模型[6] 152-166[7]。除此之外，也经常使用Tweedie(复合Poisson-gamma)分布模型直接对纯保费进行预测。但是在车险索赔数据中，由于索赔次数在0点有大量聚集，索赔额分布具有长尾性，并且还可能出现大额索赔的情况，因此本文将分别对索赔次数和索赔额建立更加具有适用性的模型。

针对索赔次数，本文分别对其建立泊松模型、负二项模型、零膨胀泊松模型、零膨胀负二项模型和Hurdle模型，并且对这些模型进行分析比较，得到合理的预测模型。针对索赔额，本文建立分类索赔模型。分类索赔模型就是将索赔额转化为大额索赔和正常索赔两类，然后分别对不同分类部分运用指数族分布(例如伽玛分布)建立模型[8] 75-126。

二、频率-强度模型概述

对索赔频率是离散的、索赔额是连续的这种混合型车险数据进行建模通常采用两步分析的方法。第一步，建立索赔频率的广义线性模型；第二步，在发生索赔的条件下，建立索赔强度模型。这种分两步方式所建立的模型称为费率厘定的频率—强度模型，也可以称为两步估计模型[9] 87-164[10-11]。

(一)索赔频率分布模型

对于广义计数分布的一种流行方法是用一个复合求和的形式，具体公式如下：

(1)

根据M和Z具体形式的选择不同，可以得到不同的分布形式。 索赔频率模型通常采用的分布为负二项分布、零膨胀泊松分布或者Hurdle泊松分布等。

1.负二项分布模型。假定N|Θ～P(λ·Θ)，其中Θ是参数为(α，α)的伽马分布(即E(Θ)=1)，那么N符合负二项分布：

n=0，1，2，…

(2)

令γ=α-1和p=(1+αλ)-1，则该负二项分布指数族的标准形式为：

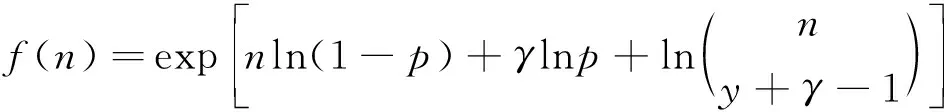
n=0，1，2，…

(3)

指数族分布中，通常令θ=ln(1-p)，b(θ)=-γln(p)和a(φ)=1。可知N的期望为：

(4)

同时，它的方差可以写成：

(5)

2.零膨胀模型。零膨胀模型用于建立大量零计数的计数数据。零膨胀计数数据模型由两部分组成：一部分为集中在零点的点概率，例如logistic模型或者是probit模型；另一部分为计数分布，例如泊松分布或负二项分布[12]。零膨胀模型通常表示为：

(6)

其中Ni为第i个体发生的次数。因此，对于一些计数模型pi(·)，例如参数为λi的泊松分布，有：

E(Ni)=(1-πi)λi

(7)

(8)

零膨胀模型也可以写成一类零调整回归模型：

(9)

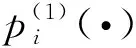
(10)

对应于上述模型的均值和方差分别为[8] 475-510：

(11)

Var(Ni)=P(Ni>0)Var(Ni|Ni>0)

+P(Ni=0)E(Ni|Ni>0)

(12)

(13)

正如索赔数量和索赔额一样，对于每个部分可以分别对其进行对数极大似然估计。

(二)索赔强度回归模型

1.GAM模型。对于索赔强度回归模型，索赔强度Y一般服从Gamma分布，其密度函数可以表示成：

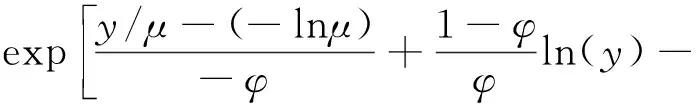
(14)

其中联结函数为θ=μ-1和b(θ)=-ln(μ)。因此，方差函数为V(μ)=μ2，进一步可得到Var(Y)=φE(Y)2。

通常情况下，车主年龄是索赔强度的重要解释变量。而广义线性模型采用的是线性结构来描述解释变量对联结函数作用后的响应变量均值的影响，没有考虑非线性结构。这与很多实际情况并不相符。另外，GLM很难处理连续型解释变量的情况。因此，当连续型解释变量以非线性影响形式存在时，通常采用广义可加模型(GAM)来进行建模[13-14]。GAM的系统部分可以表述为如下解释变量的可加形式：

(15)

其中，xj(j=1，2，…，q)是解释变量，hj(·)是样条函数(通常选为三次样条函数)。

2.大额索赔模型。通常情况下，索赔大小分布通常表现出偏斜和长尾，表明大的索赔更可能发生。当出现大额索赔时，传统的索赔强度模型会产生很大的偏差。Beirlant 和Teugels提出一种处理大额索赔的方法[15]。这情况下，把标准索赔和大额索赔分开处理是必须的，首先对是否是大额索赔建立logistic模型，进行分类，得到大额索赔的概率，然后分别对标准索赔和大额索赔建立索赔强度模型。

给定一个随机变量Z，在给定X的条件下，当Z取zi时，有：

(16)

在这里，考虑Z是索赔额，令Z属于{Y>s}或{Y≤s}。对于一个比较大的数s，有：

E(Y|X)=E(Y|X，Y≤s)·P(Y≤s|X)+

E(Y|X，Y>s)·P(Y>s|X)

(17)

其中，E(Y|X，Y≤s)是正常索赔(低于s的索赔)的期望值；E(Y|X，Y>s)是大额索赔(超过s)的期望值；P(Y>s|X)是大额索赔发生的概率；P(Y≤s|X)是正常索赔发生的概率。s作为阈值，对于P(Y>s|X)和P(Y≤s|X)部分，可以运行logistic回归模型分别进行求解。 对于E(Y|X，Y≤s)部分和E(Y|X，Y>s)部分，在数据集的子集上进行回归。

三、实证分析

(一)数据集和描述性统计

本文采用中国某一家保险公司某一省份的一年期客车数据集。该数据集包含5列，分别为：城市代码、索赔次数、赔付金额、车主性别、车主年龄，共10 000条。其中索赔次数或者赔付金额作为因变量，性别作为因子变量，将车主年龄作为数值变量，城市代码作为多水平因子变量，有5个水平变量。如表1，显示数据集前6行。

表1 索赔数据集表

注：性别中1表示男，0表示女性。

对于每个单独的驾驶员，数据集包含一年索赔数量的信息。当有索赔时，我们还可以获得相应的保险金额。表2显示不同驾驶员的索赔频率。正如预期的那样，我们观察到在一年中只有小部分的保单持有人发生意外。

表2 索赔次数表

保险数据的另一个特征是索赔额大小分布的长尾。 为了说明，表3显示了在发生索赔的条件下，每个保单年度的总索赔额的百分位数。

表3 索赔额百分比表 单位：元

为了使索赔次数和索赔额(单位为元)可视化，分别做出其直方图，如图1。

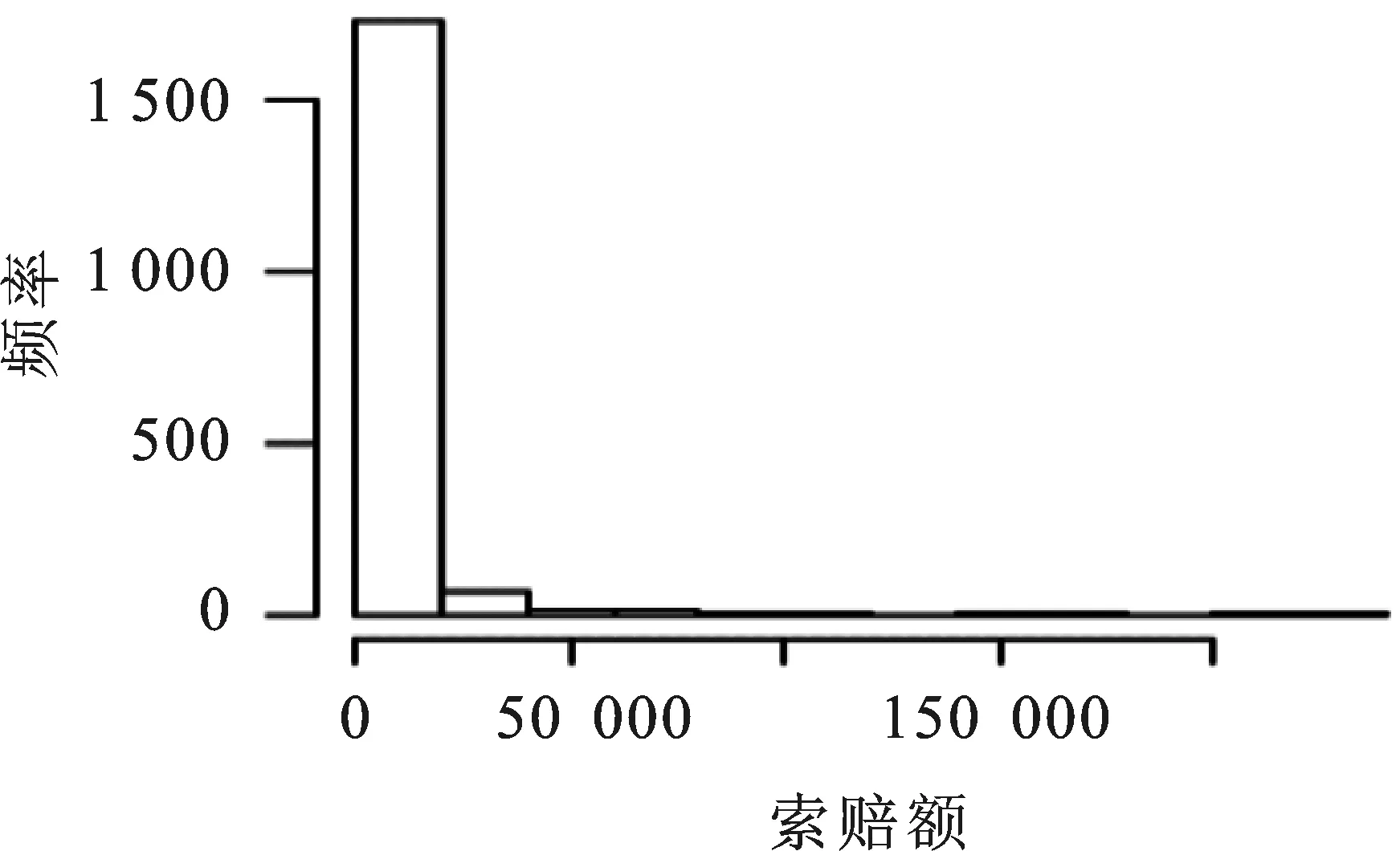
图1 索赔次数和索赔额直方图

(二)索赔频率建模

下面对索赔频率进行建模，因变量为索赔次数、城市代码、性别，车主年龄作为自变量在该模型中，由于车主年龄与索赔次数没有线性关系，因此本文将车主年龄分类，变成因子变量。本文把司机年龄转化为如下因子变量，其中，30岁以下为年龄组1，30～40岁为年龄组2，40～50岁为年龄组3，50～ 60岁为年龄组4，60岁以上为年龄组5。

本文分别对索赔频率建立泊松回归、负二项回归、零膨胀泊松回归、零膨胀负二项回归和Hurdle模型(分布为负二项分布)，如表4。

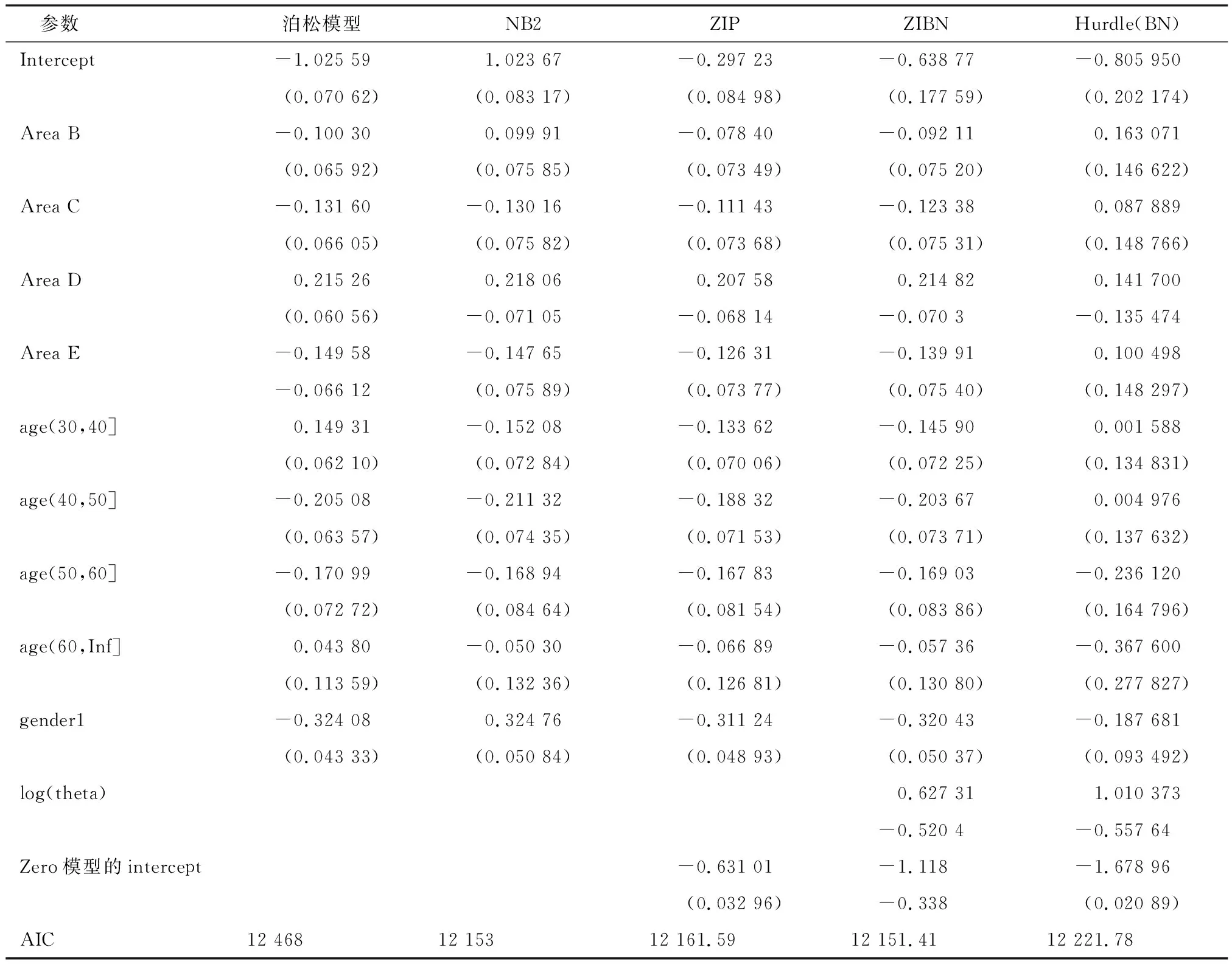
表4 单变量索赔频率模型估计表

在该数据分析中，我们研究每个保单年度的索赔总数投保人。表4显示了各种计数回归模型的估计值(括号内是标准差)，泊松和负二项模型的比较提供了与索赔计数相关的过度分离证据。零膨胀模型估计整体要优于泊松和负二项模型，通过AIC统计值，发现零膨胀负二项模型(ZIBN)效果最好。Hurdle模型在本数据中估计效果并不好。

(三)索赔强度建模

由于索赔强度模型与索赔频率模型是分开建模的，而且影响索赔强度的因素和影响索赔频率的因素通常情况下可以不一样，因此本文建立索赔强度模型时，仅仅用到与其有关的变量。通常情况下，车主年龄是索赔强度的重要解释变量。本文做出索赔强度与车主年龄的散点图，如图2。

图2 索赔强度与车主年龄的散点图

由图2可知，索赔强度与车主年龄有一定的非线性关系。年龄在25岁以下时，索赔强度比较低；年龄在25～60岁时，索赔强度较高；年龄大于60岁时，索赔强度又降低了。因此本文建立索赔强度与车主年龄的广义可加模型，其中用到三次样条函数。

由于本文重点考虑大额索赔，因此需要先将索赔额进行排序，找到大额阈值，之后再去建立大额伽玛模型。首先把索赔额从大到小进行排序，并计算出大于索赔额的和占索赔总额的比率，如表5。

表5 大额索赔数据表 单位：元

由此可知，最大的索赔额超过23万元，几乎占总损失的2%。 前6个索赔额占总索赔11%。这些车主年龄分别为33、31、36、50、54、52岁。考虑阈值s为40 000，超过这个阈值的数量不到2%。低于阈值的看作1，高于阈值的看作0，考虑logistic回归模型低于阈值概率。这个概率能被可视化，如图3。

图3 具有样条曲线的逻辑回归平滑图

对于标准和大额索赔，分别考虑两个子集的数据进行回归。为了进行对比，做一个全集数据的伽玛模型，如表6。

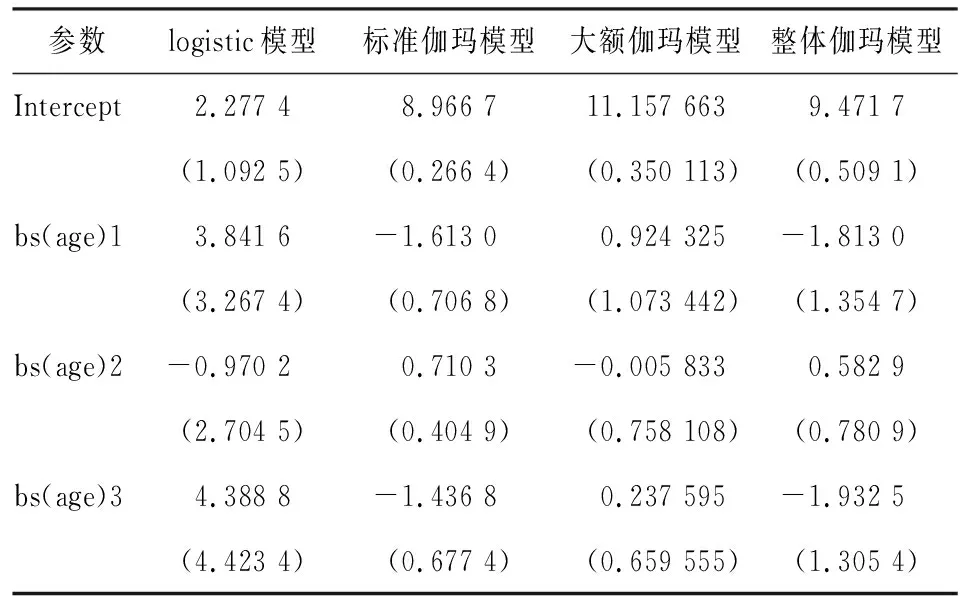
表6 单变量索赔强度模型估计表

通过表6所得系数进行预测，并将预测可视化，其中黑色曲线是整体伽玛模型，黑线是标准伽马模型预测值与其所发生概率的乘积，灰线是该两类混合模型的预测值，如图4。

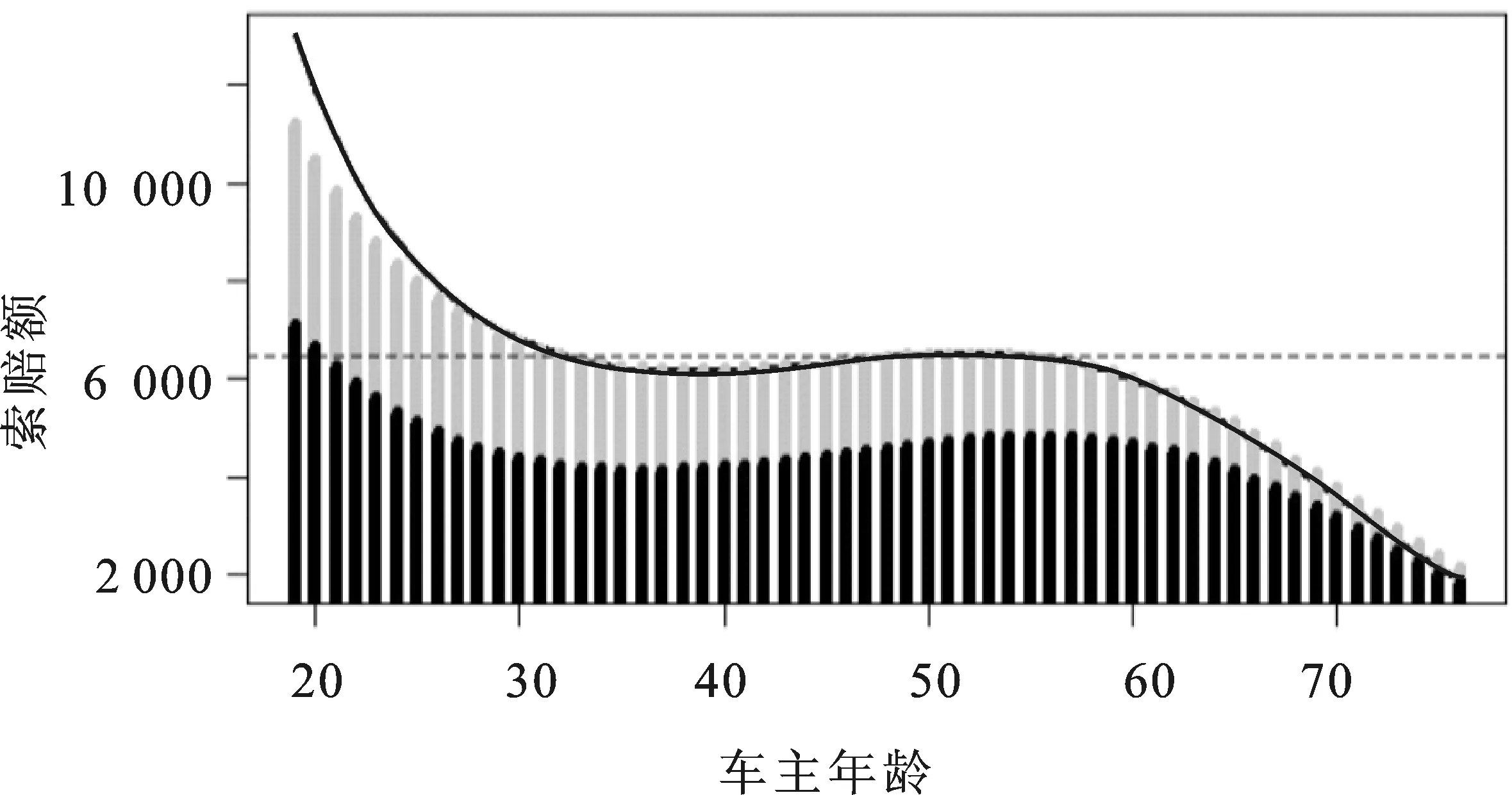
图4 索赔额关于车主年龄的预测线图

本文将预测值同真实值做比较得到图5。由图5可知，本文所建立的一般索赔模型拟合效果比较好，只不过在较高年龄时拟合效果不是很好。比较图4和图5，可知考虑大额索赔的伽玛模型比一般伽玛模型更平滑，残差更小。当大额索赔发生的概率为零时，本模型可退化为一般的索赔强度模型。

图5 预测值与真实值相对变动百分比图

四、研究结论与意义

在车险索赔中，本文采用频率—强度两步的方法，这种分开计算频率和强度的方法，有很多优点：(1)由于影响索赔频率和索赔强度的因素可以是不同的，所以分开建立模型时，两个模型可以采用不同的自变量。(2)分开建立模型，索赔频率和索赔强度可以建立多种不同的模型，从而比较并选择较优的模型，这样更灵活。

在非寿险索赔频率模型的预测中，不少实际损失数据中可能存在过离散现象或者零膨胀计数数据，为了克服这些缺点，本文分别对索赔频率建立泊松回归、负二项回归、零膨胀泊松回归、零膨胀负二项回归和Hurdle模型。然后通过比较得到较适合的模型。通常情况下，未必越复杂的模型的结果越好，针对本文数据，零膨胀负二项模型(ZIBN)效果最好。

在非寿险索赔强度模型的预测中，在实际损失额数据中，有的时候可能出现大额索赔，这个时候采用传统的伽玛分布可能就不是很适合了，本文采用Beirlant和Teugels(1992)提出的一种处理大额索赔的方法。将索赔额分成标准索赔和大额索赔两部分，从而求出两部分索赔额各自的均值，乘以对应所发生的概率，得到索赔强度的结果。当大额索赔发生的概率为零时，本文的索赔强度模型退化为一般的索赔强度模型。