单指标纵向数据模型的估计

赵明涛，许晓丽，高 巍

(安徽财经大学 a.统计与应用数学学院；b.管理科学与工程学院，安徽 蚌埠 233030)

一、引言

纵向数据是指对同一组个体在不同时间点上进行重复观测而得到的数据，纵向数据应用广泛，反映了个体间差异和个体内部的变化[1] 83-101[2] 77-86[3-4]。在社会学和经济学中，纵向数据又称面板数据[5]。重复观测会导致同一个体的观测之间存在个体内相关性，这种相关性是个体观测之间真实关系的反映，不可忽略。在实际研究中，个体内相关性是未知的。目前，对个体内相关性的研究和处理，已成为纵向数据分析的热点。

本文基于纵向数据集{(xij，yij)：i=1，2，…，N；j=1，2，…，ni}研究单指标模型[6]的估计问题，模型为：

(1)

其中，yij及xij分别为第i个个体的第j次观测相对应的响应变量和协变量，XTβ为一维单指标，β为p维单指标参数向量，亦称为投影参数向量，h(·)为一元未知联系函数，‖β‖=1，‖·‖为Euclidean模[6] 101-178。研究单指标模型的主要任务就是β的估计和h(·)的拟合。

单指标模型在金融、经济、生物和医学等领域起到了重要的作用。该模型把p维协变量进行线性组合，把所有的协变量投影到一个线性空间上，然后在该线性空间上拟合一个一元函数，可以避免多维数带来的问题[6] 101-178。

对于单指标纵向数据模型，广义估计方程(GEE)是一个有效的估计方法[4，7]。GEE将个体内相关性视为讨厌参数，仅需要模型一阶矩和二阶矩的假设条件，只要假设条件正确，一定条件下总能得到模型参数的相合的、渐近正态的估计。Tian利用GEE对纵向数据部分线性单指标模型进行了估计，提出了广义惩罚样条估计方法，建立了估计的渐近性质，得到了较好的数值模拟结果[4]。然而，GEE也存在一些缺点。如，不存在一个目标函数，估计函数不唯一，难以用于模型检验和基于似然的拟合优度检验，估计结果缺乏概率解释性。在一些特殊条件下GEE估计并非最优的[8] [9] 49-72。

二次推断函数(QIF)方法是GEE的一个强有力的竞争者[10-13]。QIF仅需要和GEE相同的假设条件，并能克服GEE的一些不足之处。例如，QIF通过矩阵基展开近似工作相关矩阵的逆矩阵，不需要对讨厌参数进行估计，降低了估计的复杂度和难度。一定条件下，QIF估计都是相合的、渐近正态的[10-13]。QIF是一个目标函数，可以利用拟合优度检验方法检验模型的二阶矩条件的正确性。形式上，QIF类似于对数似然函数，具有有限的影响函数，对待污染数据更加稳健，而GEE却不具备此类性质。

近年来，一些学者基于QIF研究了单指标纵向数据模型。Bai等提出惩罚QIF方法估计纵向数据下的单指标模型，建立了估计的大样本性质[14]。Lai等 提出了偏差修正的QIF估计参数，得到了估计方法的渐近性质[15]。Ma等研究了重复观测条件下的偏线性单指标模型，他们利用B样条基函数近似未知联系函数，然后应用QIF和截面方法，提出了基于QIF的估计量。一定条件下，该估计量具有较好的大样本性质[16]和数值表现。Li等利用偏差修正QIF处理偏线性单指标模型的变量选择问题，建立了估计方法的渐近性质，讨论了方法在有限样本情形下的表现[17]。

对于QIF方法的数值实现问题，一定条件下Newton-Raphson算法是一个有效的方法[8，10]。实际中，该算法可能由于最优权矩阵的不可逆而失败。鉴于此，Han等提出了一个修正QIF(MQIF)方法[18]。MQIF利用一个线性收缩估计替代最优权矩阵，估计总是可逆的。MQIF适用于固定设计情形，结果显示，在有限样本情况下该方法具有比QIF更高的收敛比例[18]。Westgate 和Braun改进了QIF方法，该方法在大样本和小样本情况下，都优于QIF和GEE方法[19]，适用于固定设计和随机设计情形。实际中矩阵求逆运算会使得迭代算法计算复杂度过高。鉴于此，Khan等利用割线法进行数值求解，该方法避免矩阵求逆运算具有更小的计算量[20]。

本文构造惩罚改进二次推断函数方法研究单指标纵向数据模型的估计问题，建立估计方法的渐近性质，利用割线法进行数值迭代求解。

二、模型估计方法

针对模型(1)，假设：

E(yij)=μij，var(yij)=V(μij)

其中V(·)为已知方差函数。利用多项式样条逼近联系函数h(·)。本文选用D个节点的d阶截断幂函数基对h(·)进行基函数展开近似，基函数向量为[10]：

其中τl(l=1，2，…，D)为D个节点，且

一定条件下可得到：

h(t)=B(t)Tα

(2)

其中α=[α1，…，α1+D+d]T为样条基函数系数向量。

令γT=[βT，αT] ，μi=(μi1，μi2，…，μini)T，Yi=(yi1，yi2，…，yini)T，Xi=(xi1，xi2，…，xini)T，得到：

(3)

(4)

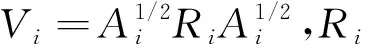
(5)

其中：

利用广义矩方法(GMM)[21]构造出关于γ的QIF

(6)

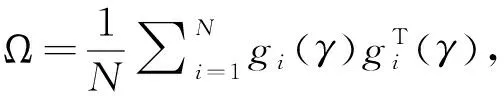
则E(ei)=0，当i≠j时，ei和ej相互独立，重新表示：

(7)

其中：

(8)

(9)

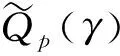
(10)

进而得到联系函数的估计为：

(11)

(12)

其中：

具体的迭代步骤如下：

三、估计方法的渐近性质

实际中，由于抽样的随机性和样本的有限性，估计结果不可能严格等于真实参数值，估计结果和真实参数之间存在偏差的事实不可避免，因此渐近性是评价估计方法的重要标准。将估计方法或估计量放在无限样本情形下讨论，此时最重要的评价标准就是相合性、渐近正态性。相合性可以保证估计量依概率收敛到真实参数，渐近正态性可以对估计量的收敛速度和渐近形态进行数量刻画。

为了满足单指标系数的可识别性，不妨设：

(13)

下面给出一些必要的假设条件：

H1：{ni}为有界正整数；

H2：权矩阵Ω→a.s.Ω0，其中Ω0为一个对称正定矩阵；

H4：Γ为紧空间，且γ0为Γ的内点；

H5：E(gi(γ))关于γ连续；

参数估计结果的理论性质受非参数拟合的影响，因此给出了非参数拟合的一些限定条件(H3、H4)。在非参数拟合满足一定的条件下，理论性质才能满足，估计结果才能在有限样本情况下表现良好。基函数的选择也有一定的限定条件，一般情形下，要求选择的基函数能很好地近似非参数联系函数，这样在讨论渐近性质时才有意义，才会获得较好的有限样本估计结果。这也是本文选择截断幂函数基的一个重要原因，该基函数为多项式样条函数，通过合理的选择节点，可以较好的拟合非参数联系函数，并且可以引入惩罚项避免过拟合问题。

下面建立估计方法的渐近性质。定理1描述估计结果的相合性，相合性可以保证在样本量充分的情况下，估计方法达到任意指定精度情况发生的概率趋近1。定理2描述估计结果的渐近正态性和有效性，描述估计结果的概率收敛速度和有效性质。

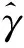
证明：由H2及式(7)可知：

由大数定律以及条件H2，可得：

当λ=o(1)时，满足：

由条件H1以及连续映射定理可得到：

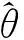
其中β0=βφ0。

证明：不妨假设：

(14)

由式(14)可知：

由中心极限定律可得到：

由泰勒公式得到：

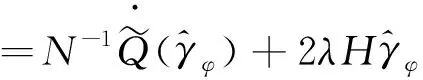
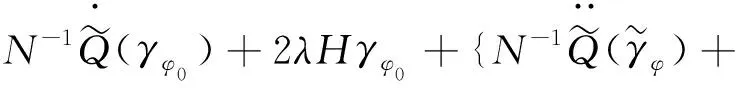
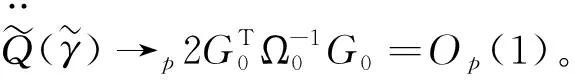
如果λ=o(N-1/2)，可得：

由上式以及条件H4可得：

因此可得到：

所以渐近正态性得证。渐近有效性可根据GMM理论直接得到，此处省略。

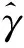
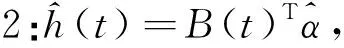
四、实际应用

(一)基函数的选择

B(t)的选择包括阶数和节点的选择。过高的阶数会造成过拟合现象，因此一般情况下阶数不超过3。节点的选择，包括节点位置的选择和节点个数的选择。节点位置一般选择等间隔法或者等分位数点法。节点个数选择不易过多，过多的节点个数会增加估计的难度和造成过拟合问题。一般情况下节点选择5个到10个之间。

(二)光滑参数的选择

光滑参数λ的选择对模型估计结果而言非常重要，λ的大小控制着模型拟合程度。实际中，利用广义交叉验证方法选择合适的λ值。定义广义交叉验证统计量[10]：

(15)

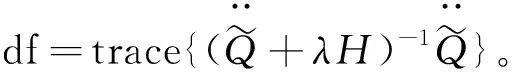
(16)

(三)数值模拟

下面通过统计模拟说明所提出的方法的实际表现。考察如下模型：

(17)

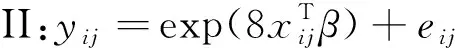
(18)

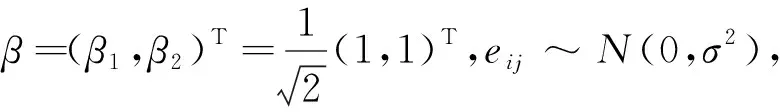
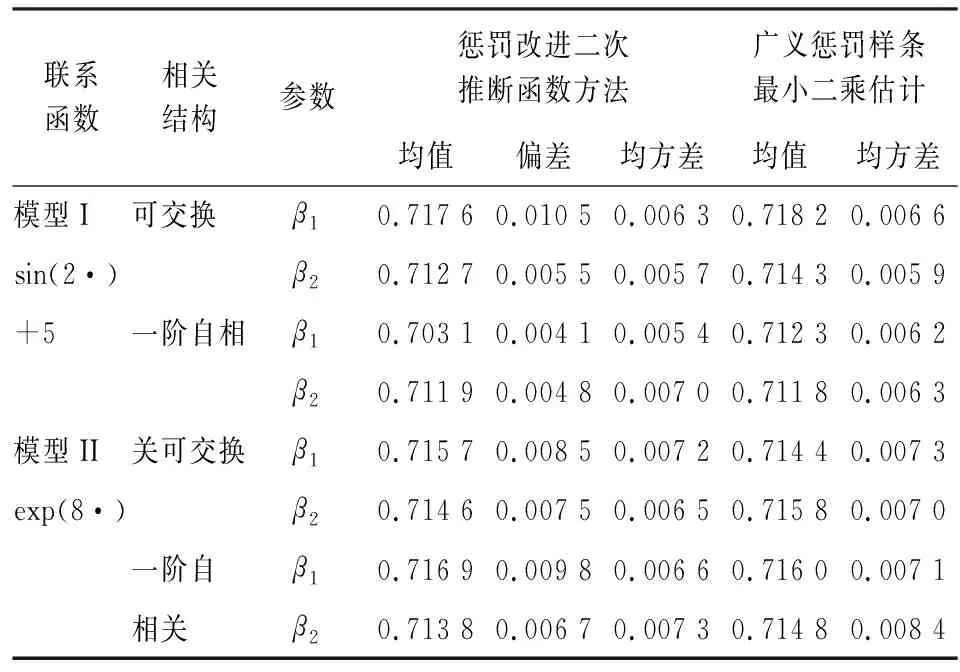
表1 β的估计结果表

表1给出了惩罚改进二次推断函数方法以及利用广义惩罚样条估计方法下的估计结果[2] 83-101[4]。表1显示在不同的工作相关矩阵条件下，本文提出的惩罚改进二次推断函数归于β的估计效果很好，精度很高。对广义惩罚样条估计的估计结果对比，在均方差意义下，本文提出的方法，在绝大部分情况下优于广义惩罚样条估计方法。

图1分别给出了不同工作相关矩阵条件下的联系函数拟合结果，实线为真实的联系函数曲线，虚线为拟合曲线。横坐标为单指标的取值，纵坐标为联系函数的取值。从图1中可以看出，模型I和模型II联系函数的拟合效果良好，说明有限样本情况下估计方法对于估计未知联系函数的实用性和价值。从图中也可以看出，模型I的估计效果要比模型II的估计效果更好一些，主要是因为在单指标的取值区间内，模型I的联系函数取值区间较小且函数图像更接近多项式函数。因此在利用截断幂函数基近似联系函数时，估计效果更好。

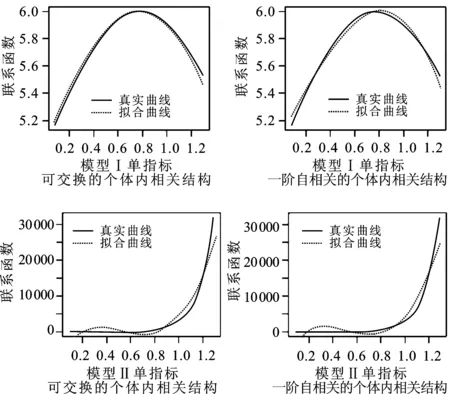
图1 联系函数拟合图

(四)实例数据分析

利用本文方法研究癫痫病突发研究案例数据[14，22]，目的在于根据观测数据研究药物是否能降低癫痫病发病率。响应变量为两周内的癫痫病突发次数。协变量包括对数化年龄(X1)、基本突发数(X2)、治疗方法(X3)、治疗方法和基本突发数的交互效应(X4)。基本突发数是在原始突发数据的基础上除以4再取对数得到；治疗方法取0表示病人服用安慰剂，取1表示病人服用药物。原始数据的工作相关矩阵选择一阶自相关结构。Xi(i=1，2，3，4)对应的单指标参数为βi(i=1，2，3，4) 。

根据Bai等人的研究[14]，利用含有4个节点2阶截断幂函数基拟合真实数据。对比广义惩罚样条最小二乘估计方法、惩罚二次推断函数方法和惩罚改进二次推断函数方法的估计结果。具体估计结果如表2。根据表2及Bai等人的研究[14]，本文提出的方法与惩罚样条最小二乘估计、GEE、惩罚二次推断函数方法的估计结果基本上相互一致，所有的协变量均显著。实例说明，惩罚改进二次推断函数适用于纵向数据下单指标模型的参数估计问题，该方法具有一定的实用价值。

表2 实例数据估计结果表

五、结论

纵向数据(面板数据)是复杂数据的一种。纵向数据结合了多元数据和时间序列数据的特点，但与二者不同：同一个体的不同观测之间的内相关具有时间序列的特点，因此纵向数据不同于经典的多元数据；纵向数据往往是由来自于每一个个体观测的大量短序列组成，而时间序列数据往往是一个简单的长序列[2]。特殊的数据结构，使得纵向数据存在未知的个体内相关，个体内相关性的研究和处理是纵向数据研究的重点。一定条件下，二次推断函数方法可以巧妙地解决这个问题。

单指标模型，是一类重要的半参数降维模型，该模型被广泛运用于复杂数据的有效推断上。本文首次构造惩罚改进二次推断函数方法对单指标模型中的未知联系函数和单指标系数同时进行估计，主要是对惩罚改进二次推断函数的理论性质和应用特点做一个有效的推断和验证。该方法弥补了二次推断函数和修正二次推断函数的一些不足之处，适用于随机设计和固定设计情形下的纵向数据模型，具有很强的理论价值，如相合性、渐近正态性和有效性。实验结果证明，该方法具有良好的模拟结果，具有一定的应用价值。不仅如此，该方法还具有较强的外推性，可以用于相关性数据(纵向数据、面板数据、重复测量数据)下的其它参数或半参数模型的估计，如变系数模型、可加模型、偏线性可加模型等。