印制电路板环境应力筛选费用模型优化仿真★

刘文杰，金健，张航军，黄思涵

(华中科技大学机械科学与工程学院，湖北武汉 430074)

0 引言

环境应力筛选是可靠性试验项目之一，通过对产品施加合适的环境应力，可以有效地剔除产品中的潜在缺陷，使产品尽快地进入偶然失效期，提高产品使用阶段的可靠性。根据以往的经验，当出现失效时，在较低组装级上进行维修，维修费用会较低。组装级提高一级，维修费用几乎会提高一个数量级。而当产品投入使用后出现失效时，维修的费用会更高[1]。进行环境应力筛选，可在产品投入现场使用之前，把产品生产过程中引入的潜在缺陷剔除，不仅可以大大地减少维修费用，还能提高产品在用户中的口碑。然而，当产品已经进入偶然失效期后，其使用可靠性已经接近于设计可靠性，此时若仍过度地对产品进行应力筛选，其可靠性不仅不能再得到太大的提升，反而会因为筛选时间过长而使得产品的生产成本大大地增加，得不偿失。因此，进行环境应力筛选，需要合理地制定环境应力筛选计划。

本文以印制电路板组件为例，研究生产和使用阶段环境应力筛选的费用估算和相应的优化问题。使用术语连接来描述在组件级装配过程中可能会引入缺陷的要素[2]。以二级组装模型来建立印制电路板的费用模型，即以印制电路板上所使用的元器件为元器件级，以印制电路板、元器件和涉及的连接作为组件级，假设元器件级的缺陷来源于元器件，组件级的缺陷来源于元器件和连接。

针对环境应力筛选费用模型优化问题，国内外的研究学者已经进行了一系列的研究。Li Fang针对电子元器件的环境应力筛选提出了一种优化模型。他使用混合分布法来对元器件失效现象建模，使用罚函数法，通过进行环境应力筛选而使得可节省的费用最大化来求最佳的筛选时间[3]。Edward A Pohl针对由元器件级、印制电路板级和系统级组成的复杂系统提出了一个3级混合分布模型，使用指数分布法和威布尔分布法来对其寿命特性建模。使用拟牛顿法求解费用模型的最优解可得到各级最佳的筛选时间[2]。但以上两种方法所使用的指数分布和威布尔分布模型的失效率并不符合产品早期失效期的特点。Li Yan则针对一个由元器件级和组件级组成的二级系统提出了环境应力筛选和老化相结合的方法来剔除早期故障，并使用浴盆曲线来对产品的寿命特性进行建模[4]。但他的仿真实例却假设产品没有早期失效期。

由于威布尔分布具有极强的适应性，为了描述产品在早期失效期的失效率情况，使用形状参数小于1的两参数威布尔分布来描述元器件和连接早期失效期和偶然失效期的寿命特征[5]。

1 组件筛选模型

对于印制电路板组件，本章将建立一个由元器件级和组件级组成的二级应力筛选模型。为了较好地描述产品的失效率情况，假设元器件和连接的寿命都服从两参数威布尔分布，并且元器件和连接都分别包含一定比例的次品和合格品，假设次品与合格品相比，有较高的失效率。根据文献 [1]的要求，在环境应力筛选过程中，会对产品施加超过常规使用环境中的环境应力，并且不会引入新的故障模式，也不会引入新的潜在缺陷，只是把已经存在的潜在缺陷加速转化成为故障并剔除掉。

1.1 元器件级筛选

元器件级筛选的目的是把含有潜在缺陷的元器件，即次品，从整批元器件中剔除出去，使得产品能尽快地进入稳定期。只有通过了元器件级筛选的元器件才能被组装到印制电路板中。

环境应力筛选对元器件施加的应力水平会高于正常使用时环境对产品施加的应力水平。为了描述元器件在环境应力筛选过程中的寿命加速效果，使用加速因子的概念。因此，在环境应力筛选的应力水平下，元器件级等效使用时间与加速因子相关，即：

式(1)中：tc——元器件级等效使用时间；

tac——元器件级筛选时间；

Kc——元器件级筛选加速因子。

加速因子定义为在不同应力水平作用下产品达到相同寿命消耗累积量的期望时间之比[6]。Kc值的大小取决于所采用的加速应力类型和应力水平。周玉芬曾推导过环境应力筛选加速因子的计算公式，并且针对温度循环应力，给出了相应的参数值，计算出其加速因子可达到4.99甚至更高[7]。

由于元器件的寿命服从威布尔分布，则其可靠度函数为：

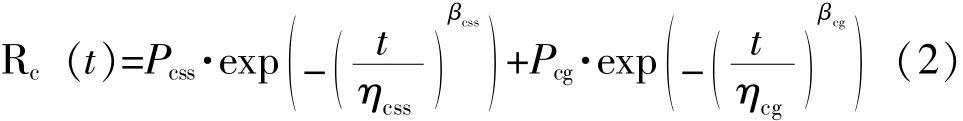
式(2)中：Pcss、Pcg——元器件中次品和合格品所占的比例；

βcss、 ηcss、 βcg、 ηcg——元器件次品和合格品威布尔分布的形状参数和比例参数。

并且：

元器件通过tc时间的筛选后为次品的概率和合格品的概率分别为：

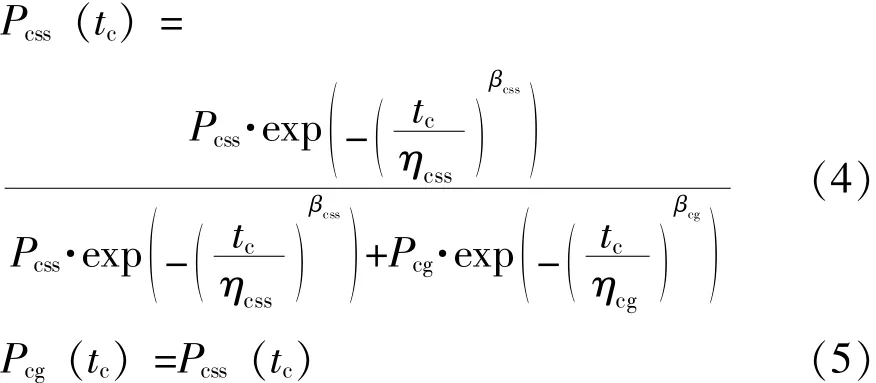
通过了元器件级筛选的元器件将被组装到组件中。在元器件级筛选中失效的元器件将被已通过筛选的元器件替换。预计的元器件更新数可由更新理论求得[8]。更新方程如下：

式(6)中：F(x)——元器件寿命的累积失效分布函数；

f(x)——失效概率密度函数；

M(x)——在[0，t)时间内预计的元器件更新数。

求解更新方程需要使用拉普拉斯变换，但是威布尔分布的拉普拉斯变换很难求解，因此可采用数值方法求解。R Jiang使用伽马分布与正态分布结合的方式求解威布尔分布的更新方程值，其方法适用于威布尔形状参数β∈ (0.87，8.0)的情况，并且误差小于0.003 7[9]。其使用威布尔累积失效分布函数F(t)的形状参数、比例参数和t值来估算M(t)值。则在经历过tc时间筛选后，t时间内预计的元器件更新数为：

其中， Mcss(t｜tc) 和 Mcg(t｜tc) 可分别根据次品和合格品元器件的累积分布函数来估算。

1.2 组件级筛选

组件级上的缺陷主要来源是元器件和连接。同元器件级筛选一样，组件级的应力筛选同样会对元器件和连接造成寿命加速效果，可用一个加速因子来描述。连接和元器件在组件级筛选下的等效使用时间可用下面的关系来表示：

式(8)中：tab——组件级筛选时间；

Kb——组件级筛选加速因子。

假设所有的连接中都包括了合格品和次品，其寿命都服从威布尔分布。其未筛选的连接的可靠度函数为：

式(9)中：Pbss、Pbg——连接中次品和合格品所占的比例；

βbss、ηbss、βbg、ηbg——连接次品和合格品的形状参数和比例参数。

连接通过tb时间的筛选后为次品和合格品的概率分别为：

因此，通过筛选的连接的可靠度函数为：

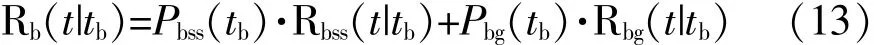
式(13)中：Rbss(t｜tb)——连接次品通过tb时间筛选后的可靠度函数；

Rbg(t｜tb)——元器件合格品通过tb时间筛选后的可靠度函数。

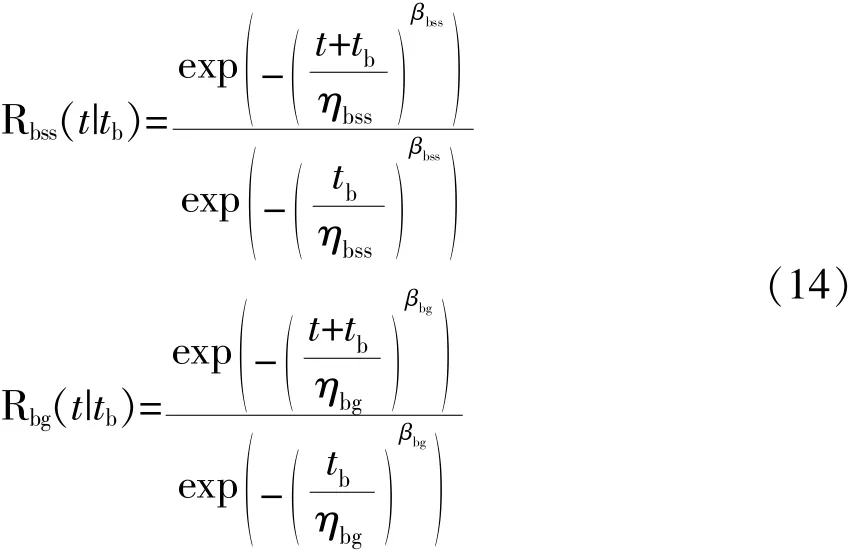
当连接发生失效时，就对其进行维修。失效率的定义为某产品工作到某时刻t时尚未发生失效，在该时刻t之后的下一个单位时间内发生失效的概率。则某一时间段连接的维修数可由对其失效率函数λ(t)积分来估算[2]，其关系式如下：

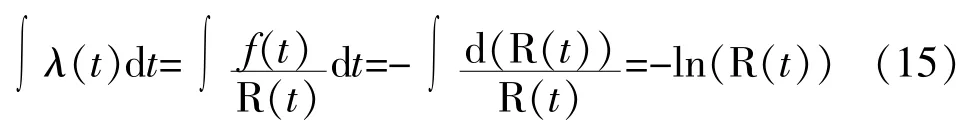
式(15)中：f(t)——失效概率密度函数；

R(t)——可靠度函数。

经过tb时间的组件级筛选后，连接的预计维修数为：

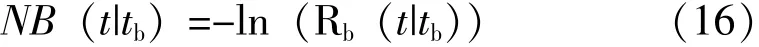
2 总费用模型

对环境应力筛选总费用进行优化，首先，需要建立印制电路板从生产到保修期结束期间的费用模型，找出影响总费用的因素，并研究各种因素是如何影响总费用的；然后，在此基础上，找出总费用最低值，制定最优的应力筛选计划。印制电路板整个寿命周期内的费用可分为元器件费用和组件费用两部分，则总费用为：

2.1 元器件费用

元器件费用由固定费用、随时间增长的筛选费用，以及分别在元器件级筛选、组件级筛选和现场使用且在保修期范围内更换元器件的费用。对于更换元器件的费用，其所处的组装级越高，更换费用就越高。因此，对于存在潜在缺陷的次品元器件，应及早将其筛选出来。但是在实际的应用过程中，依然存在即使潜在缺陷已经转化为故障，却仍然没有被检测出来的情况，所以在各个组装级中筛选时检测效率也会受到一定的影响。元器件级费用计算公式如下：

式(18)中：SC——元器件级筛选的固定费用；

I(t)——t＞0表明开启筛选设备；

npcb——印制电路板的数量；

nc——每块印制电路板上元器件的数量；

CT——单个元器件在元器件级筛选中单位时间的费用；

DC——元器件级筛选的检测效率；

CRCC——在元器件级筛选时更换单个元器件的费用；

DB——组件级筛选的检测效率；

CRCF——在现场使用时更换单个元器件的费用。

2.2 组件费用

印制电路板上的费用主要来自于各个连接的失效，包括筛选设备的固定费用、组件级筛选时随时间增加的费用、维修在组件级筛选中失效并被检测到的连接、维修在投入使用后且在保修期内失效的连接的费用。组件级费用的计算公式如下：

式(19)中：SB——组件级筛选的固定费用；

nb——每块印制电路板上连接的数量；

CRBB——在组件级筛选时维修单个连接的费用；

CRBF——在现场使用时维修单个连接的费用。

3 基于粒子群算法的费用模型问题求解

根据式 (17)的总费用模型，通过调整筛选时间tac和tab可得到不同的费用结果。因此，将筛选时间tac和tab作为优化问题的优化变量，采用优化算法寻找一种最优的筛选时间，使得总费用最少，即可实现环境应力筛选时间的最优设计。

该非线性优化问题可使用粒子群算法求解。粒子群算法 (PSO：Particle Swarm Optimization)[10]是一种进化计算技术，由Eberhart博士和Kennedy博士发明，其源于对鸟群捕食行为的研究。PSO是从随机解出发，通过迭代寻找最优解，通过自定义的适应度函数来评价解的品质，通过追随当前搜索到的最优值来寻找全局最优。这种算法具有实现容易、精度高和收敛快等优点。该问题的适应度函数定义为总费用函数。然而PSO仍然存在收敛于局部最优解的问题，而采用动态惯性权重法可较好地解决这个问题[11]，即：

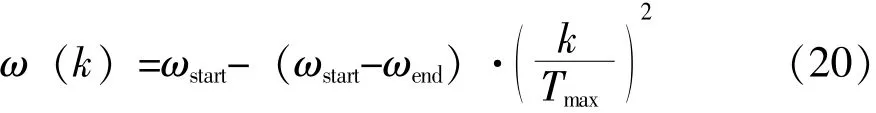
式(20)中：ωstart——初始惯性权重；

ωend——迭代至最大次数时的惯性权重；

k——当前迭代代数；

Tmax——最大迭代数。

PSO的流程图如图1所示。

图1 PSO流程图

本节将提供一个实例来阐述各个参数是如何影响产品寿命周期总费用的。假设一个生产商需要生产某种印制电路板npcb块，每块印制电路板由nc个元器件和nb个连接组成，并且假设各个参数为：

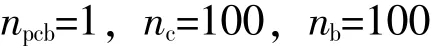
元器件和连接的威布尔分布模型参数分别如下：

元器件级筛选和组件级筛选的加速因子可根据相应的筛选应力和参数，结合阿伦尼斯模型或逆幂率模型等求得，在本例中，假设：

3.1 更新数和维修数

元器件在某个筛选时间情况下的更新数可由式(7)求得。先分别假设元器件级筛选时间为0、500、1 000、1 500 h，观察不同筛选时间对更新数的影响。更新数与时间的关系如图2所示。由图2可知，由于元器件级筛选会将一部分具有潜在缺陷的元器件剔除，使得次品元器件的占有率降低，从而影响整批元器件的累积失效分布函数，进而使得整批元器件更新方程的解值减小。因此，经历过应力筛选的元器件更新数会远低于没有经历过筛选的元器件。而当筛选时间超过1 000 h时，更新数减小的幅度就并不明显了。

对于印制电路板上的连接，当其发生失效时，并不是采取更新的策略，而是对其进行维修。在不同筛选时间后某一时刻连接的预计维修数可由式(16)求得。在不同的筛选时间下，连接预计维修数与时间的关系如图3所示。在投入使用初期，连接的维修数会急剧地增加，在一定时间之后，其增速会放缓。而对于未经筛选的连接，其维修数会远远地高于经过筛选的连接。当筛选时间超过1 000 h后，不同筛选时间后的维修数的变化幅度不大。

由图2-3可知，对元器件和组件进行环境应力筛选，可极大地减少投入使用后元器件的更新数和连接的维修数。虽然进行应力筛选会有一定的成本，但能极大地减少更新和维修费用，可见对其进行环境应力筛选是很有必要的。

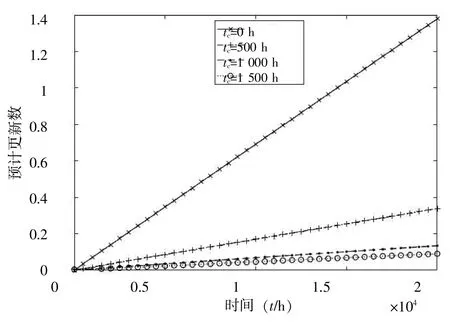
图2 元器件的预计更新数曲线

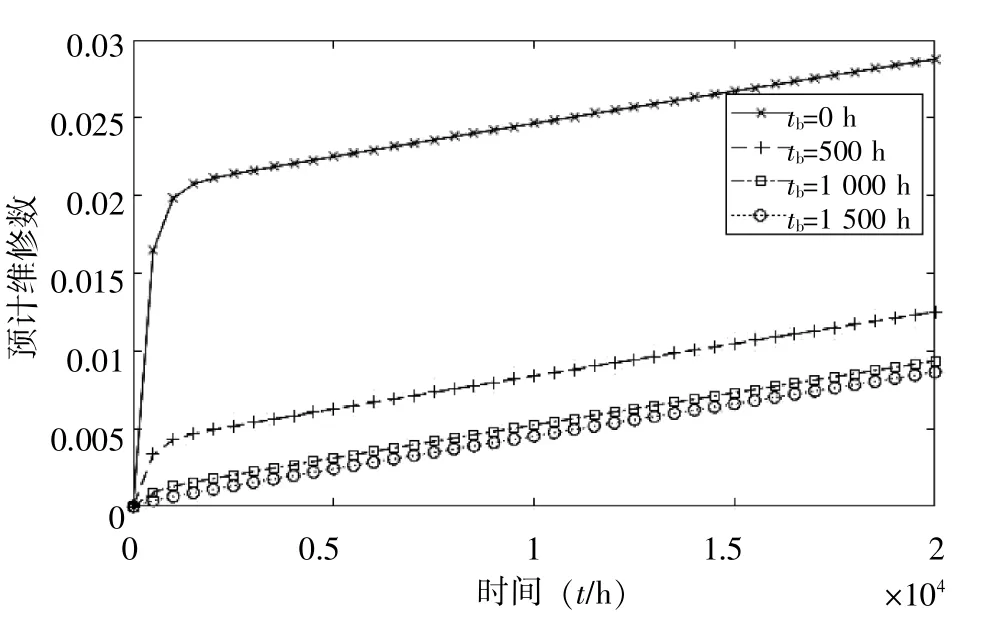
图3 连接的预计维修数曲线

3.2 数值仿真分析

根据以上提出的方法，在Matlab中实现算法程序，用于求解该总费用优化问题。在本实验中，让程序重复运行20次，可得到相同的结果，证明已求得全局最优解。

依次改变元器件级筛选和组件级筛选的加速因子，求得的结果如表1所示。

表1 加速因子的影响

案例1的总费用值随迭代次数的收敛曲线如图4所示。

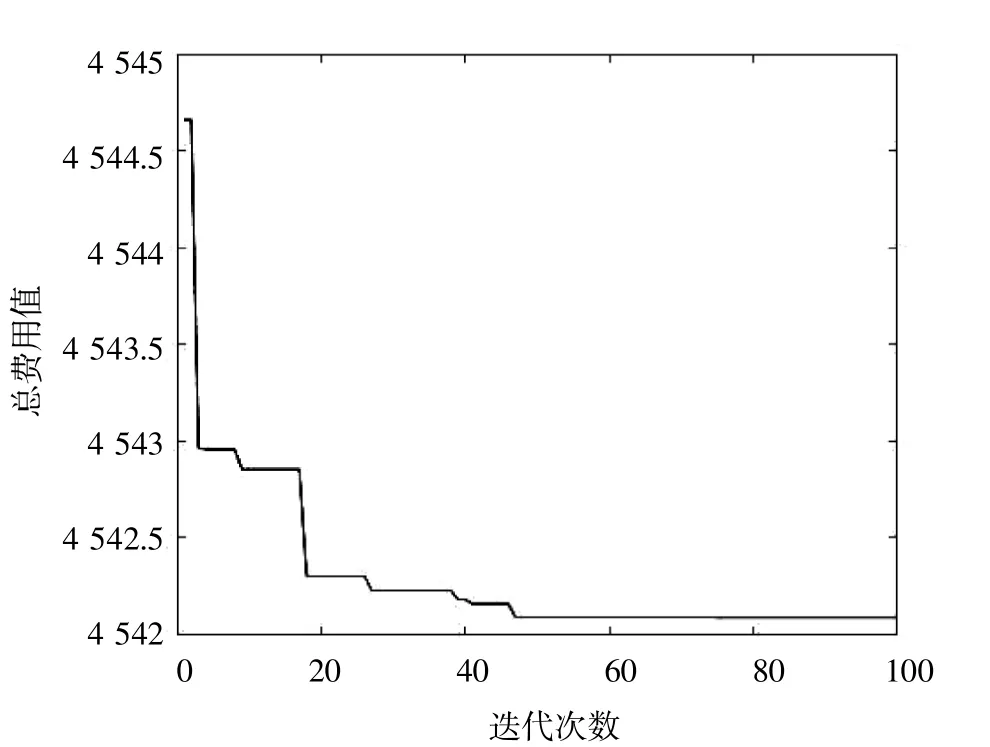
图4 PSO收敛曲线

由案例1-3可知，保持组件级筛选的加速因子不变，当元器件级筛选的加速因子逐渐地增大时，总费用减少，所需要的筛选时间减少。同理，当保持元器件级筛选的加速因子不变时，组件级筛选的加速因子增加也可减少总费用。对比案例2、4和7、8可发现，在组件级加速可取得更好的效果，因为组件级筛选可同时对元器件和连接产生加速效果。对比案例1和10可发现，当不进行应力筛选时，总费用会远远地高于筛选后的费用。因为不进行应用筛选潜在缺陷就不能被提前剔除，只会在使用现场暴露出来。而在使用现场维修会产生高额的费用。在环境应力筛选过程中，要求所施加的应力水平不能超过产品的破坏极限，以免对产品造成额外的寿命损耗。

在应力筛选过程中，将潜在缺陷剔除需要两步。第一步是通过环境应力将潜在缺陷转化为明显缺陷，第二步是将明显缺陷检测出来并维修。为了度量检测的充分程度，将由规定检测程序发现的缺陷数与筛出的总缺陷数的比值定义为检测效率。检测效率的大小决定了能否将已被应力加速变成故障的潜在缺陷找出来并准确地排除[1]。筛选在较高组装级时，由于有可能利用较现成的测试系统或机内检测系统，高组装级能准确地模拟各种功能接口，以及便于规定合理的验收准则，容易实现高效率的检测，提高检测效率。检测效率对总费用的影响如表2所示。

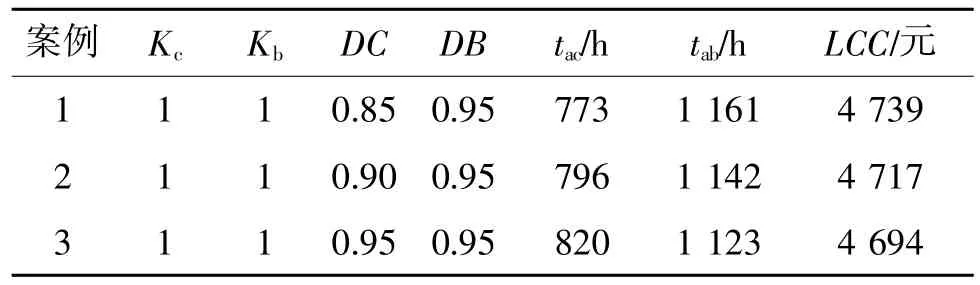
表2 检测效率的影响

由表2中的案例1-3可知，当组件级筛选检测效率相同时，元器件级检测效率越大，则总费用越低。并且，当元器件级检测效率较小时，应适度地减少元器件级的筛选时间。

由以上分析可知，检测效率是应力筛选的重要因素。施加的环境应力把潜在缺陷变成明显缺陷后，剔除故障的能力仅取决于仪表寻找故障并加以定位的能力。因此，应尽可能地采用检测效率高的测试仪表。

4 结束语

a)本文以印制电路板为例，提出了一个2级威布尔分布环境应力筛选费用模型，第一级为元器件级，第二级为组件级，组件级包括印制电路板上的元器件和连接。模型假设元器件和连接的寿命服从两参数威布尔分布，并且形状参数小于1，可较好地描述其在早期失效期失效率的表现。通过对该模型建立产品寿命周期的总费用模型，以元器件级筛选时间和组件级筛选时间为优化变量，以总费用最少为目标，使用PSO求得最优解。

b)环境应力筛选的关键是将整批产品中的次品剔除出去，因而其能减少产品随后的更新数和维修数，从而极大地减少产品在保修期期间的更新费用或维修费用。但无限制地增加筛选时间并非最佳决策。因此，只有合理地制定和实施环境应力筛选计划，才是划算的。

c)使用PSO求解总费用模型的非线性优化问题，通过对最优解分析可知，提高各级筛选的加速因子和检测效率，对于减少总费用有着非常积极的效果。因此，为了提高环境应力筛选的效益，可从此方面进行优化。

本文提出了一种用于求解环境应力筛选最优筛选时间的方法，所用的模型并不特指某种特定的产品，所涉及到的威布尔分布参数、次品占有率和费用模型中的常数可根据具体的情况来确定。