田口方法在永磁同步电机结构优化中的应用

温嘉斌 于岚

摘 要：针对永磁电机传统局部优化方法不能实现多目标优化的问题，提出了一种基于田口方法的优化方法。通过运用田口方法对分数槽集中绕组永磁同步电动机的气隙长度、极弧系数、永磁体厚度、定子齿宽和槽口宽度进行优化，使电机效率、齿槽转矩、单位质量永磁体产生转矩等性能最佳。利用田口正交实验建立正交矩阵，并结合统计学，分析各优化变量对优化目标的影响，最终得出多优化因子的最佳组合。利用有限元法对优化后的电机进行二维瞬态场分析，得到电机在负载条件下磁场分布以及相关特性。实验数据及相关分析表明，田口方法适用于分数槽集中绕组永磁同步电机的优化设计，并且能有效地抑制电机的齿槽转矩。

关键词：分数槽集中绕组;永磁同步电机;田口方法;有限元分析;优化设计;齿槽转矩

DOI：10.15938/j.jhust.2019.05.012

中图分类号： TM351

文献标志码： A

文章编号： 1007-2683（2019）05-0064-06

Abstract：Aiming at the issue of the traditional local optimization method of permanent magnet motor can not achieve multi-objective optimization， an optimization method based on Taguchi method is proposed. By using Taguchi method， air gap length， pole arc coefficient， permanent magnet thickness， stator tooth width and slot width of the fractional-slot concentrated winding permanent magnet synchronous motor are optimized， which makes performances including efficiency， cogging torque， torque produced by unit mass permanent magnet of the motor optimum. The orthogonal matrix is established according to the Taguchi orthogonal experiment. Combining with statistics， the influences of each optimization variable on the optimization objective are analyzed ， and the optimal combination of multiple optimization factors are obtained at finally. Two-dimensional transient field of the optimized motor is analyzed by using the finite element method， the magnetic field distribution and relevant characteristics of the motor under load conditions are obtained. Experimental data and related analysis show that the Taguchi method is suitable for the optimal design of fractional-slot concentrated winding permanent magnet synchronous motor， and can effectively suppress the cogging torque of the motor.

Keywords：fractional groove concentrated winding;permanent magnet synchronous motor; taguchi method; finite element analysis; optimization design; cogging torque

0 引 言

高性能釹铁硼永磁材料的出现及其性能的日益提高和电力电子设备的快速发展为永磁同步电机的设计、制造和应用创造了良好的条件[1]。与传统的电励磁电机相比，永磁电机，特别是稀土永磁电机具有结构简单，运行可靠;体积小，质量轻;损耗少，效率高;电机的形状和尺寸可灵活多样等显著优点[2-5]。分数槽集中绕组永磁同步电动机制造工艺简单、成本低，应用较为广泛，因此对于此类电机的优化尤为重要。

电机优化设计是在满足特定约束条件下，利用数学模型，寻求最佳方案，使电机性能达到最优的电机设计技术。电机优化设计方法可分为全局优化和局部优化。全局优化方法包括遗传算法、粒子群优化算法、蚁群算法、模拟退火算法等智能优化方法。文[6]采用遗传算法对应用于电动车上的内置式永磁同步电动机进行优化。文[7]提出利用搜索能力强、收敛速度快的多种群遗传算法来优化无铁心永磁直线同步电动机尺寸。文[8]提出了一种改进遗传蚁群算法，有效的提高了遗传算法求解精确解的速度。文[9]以有限元分析为基础，利用粒子群优化算法，分析出对于直线振动发电机，较大的永磁体外径可以提高材料的利用率。虽然这类全局优化方法可以包含所有不确定因素，但优化目标函数的建立非常复杂，且计算周期长。而局部优化方法计算周期短但是只能进行单一变量优化。因此本文采用田口方法对电机进行优化设计。

田口方法是一种局部优化的设计方法，与其他局部优化方法的区别在于能实现多目标优化，通过建立正交表，能在最少的实验次数内搜索出多目标优化设计时的最佳组合[3]。文[10]提出采用田口方法可应用于内置式永磁同步电动机的优化设计中，但仅对永磁体形状进行优化。文[11]也仅仅对内置式的永磁同步电动机进行优化。文[12]仅对无刷直流电动机的永磁体形状和定子齿形状进行优化，未考虑其它参数的影响。文[13]通过优化无刷直流电动机的定子齿形状和极弧与极距比来提高电机转矩的鲁棒性。文[14-16]虽然优化的都是永磁同步电动机，但并没有对分数槽集中绕组永磁同步电动机进行优化。本文利用田口方法对面包式转子磁路的分数槽集中绕永磁同步电动机进行多目标优化设计。以电机气隙长度、极弧系数、永磁体厚度、定子齿宽和槽口宽作为优化变量，效率、齿槽转矩和单位质量永磁体产生的转矩作为优化目标，建立正交矩阵，通过对优化目标进行平均值和方差分析，确定最佳方案。

1 田口方法

田口方法（Taquchi）是日本田口玄一博士开发的一种实验方法，是一种基于局部优化思想的低成本、高效益的质量工程方法，它强调产品的质量是通过设计，而不是检验[17]。田口方法是一种有健稳性优化设计方法，用正交表安排实验方法，以误差因素模拟制造成产品质量波动的各种干扰，通过对各种实验方案的统计分析，找出干扰能力最强、调整性最好、性能最稳定、可靠的设计方案。田口方法优化过程如图1所示。

1.1 优化目标及优化因子的选取

优化目标是实验中的因变量，它能反映实验的好坏。田口方法可以实现多目标优化，因此可以选择电机效率、转矩脉动等性能指标作为优化目标。

优化因子是实验中的自变量，是优化目标函数的条件。在选择优化变量时，需要选择对电机的性能影响较为明显的参数[8，18]。针对永磁同步电动机来说，永磁体为电机提供能源，永磁体的尺寸对电机性能影响较大，因此选取永磁体厚度作为其中一个优化因子;电机空载损耗随磁密的分布而变化，电机的磁密大部分分布在齿上，且变化较大，因此选取定子齿宽作为一个优化因子;气隙是传递能量的媒质，气隙磁压降占总的磁压降比重较大，因此选取气隙长度作为一个优化因子;定子槽口宽度对永磁电机齿槽转矩影响明显，因此选取定子槽口宽作为一个优化因子;极弧系数影响电机的气隙磁密分布以及磁路的饱和程度，因此选择极弧系数作为一个优化因子。

1.2 确定优化因子优选范围及水平值

在RMxprt模块，将优化因子参数化，得到优化目标在不同优化因子下的性能曲线，根据曲线分析，确定优化因子的优选范围。根据优选范围等距的选取优化因子水平值，一般选取3～5个，各优化因子的水平值按照从小到大的顺序分别取名为水平1、2、3等。

1.3 构建正交表及安排正交实验

正交实验可以对多因素水平进行优化，具有均匀分散、整齐可比的重要特点，能很大程度上减少试验次数、节约试验成本[19-20]。正交表是正交实验的关键。正交表的构建有专门的算法，不同因子的排列组合出现的概率都是相同的。建立正交表时，需要用到排列组合及概率等相关数学知识，根据建立的方法不同，试验次数也大不相同，如果选择方法不当，会使试验次数增加，从而增加实验成本。因此合理选择正交表是至关重要的。

正交表一般可以表示为Ln（Ak），其中：n表示实验次数;A表示水平值数;k表示优化因子个数。例如L16（45）表示有5个优化因子，每个优化因子选取4个水平值，一共进行16次实验。如果要进行全面实验，总共需45=1024次实验，而采用田口方法能大大降低了实验的次数。

根据正交表进行有限元仿真实验，得到优化因子在不同组合下的优化目标值。

1.4 平均值分析

为了分析优化因子的改变对电机各个性能指标的影响，以及影响所占比重，首先要分析优化因子在不同水平值下的平均值。例如电机效率在气隙为水平1时的平均值为

1.5 方差分析

方差值表示某一数据偏离平均值的程度，通过方差分析可以分析出优化因子对性能指标的影响比重。方差分析时首先要计算出各性能指标全体平均值（SS），计算如式（2）所示。其次计算各方差（SSF），公式如式（3）所示。

2 基于田口方法的电机结构优化

以一台10极12槽的分数槽集中绕组永磁同步电动机为研究对象，表1给出了该电机的基本参数。采用田口方法对电机结构参数进行优化，通过优化气隙长度、极弧系数、永磁体厚度、定子齿宽及槽口宽度，以提高电机的性能。

2.1 电机基本结构

本文研究对象为分数槽集中绕组永磁同步电动机。为了有效抑制电机的齿槽转矩，转子磁路采用面包式结构。电机基本结构如图2所示。

2.2 优化过程

2.2.1 优化因子及优化目标的确定

针对分数槽集中绕组永磁同步电动机，选取电机效率η、齿槽转矩Tc、单位永磁体产生的转矩Td作为优化目标。由于气隙、永磁体及定子槽尺寸对电机性能影响较大，所以选取气隙长度δ、永磁体厚度hm、极弧系数αp、定子齿宽bt和槽口宽Bs0作为5个优化因子。

2.2.2 优选范围及水平值的确定

利用RMxprt模块对优化因子进行优选，得到优化因子优选范围，如表2所示。在各优化因子的优选范围内等距的选取4個水平值，水平值按照从小到大的顺序分别命名为水平值1、2、3、4，各优化因子水平值如表3所示。

2.2.3 建立正交实验

根据表3及正交表的构建原则来建立L16（45）正交表，并利用有限元法建立16个电机模型，实验结果如表4所示。

2.2.4 数值分析

数值分析包括平均值分析和方差分析。根据式（1）及表4可计算出优化因子在不同水平值下的电机性能平均值，计算结果如表5所示。根据式（2）、式（3）以及表5可计算出优化因子在性能指标下的方差及其所占比重，如表6所示。

顯然，Bs0对电机效率η 影响最大，δ、hm、bt、Bs0对电机齿槽转矩Tc影响较大;αp、hm、bt对单位质量永磁体产生的转矩Td影响较大。

根据表5可知，分别使电机效率最大、电机齿槽转矩最小、单位永磁体产生的转矩最大的优化因子组合为δ（4） αp（2） hm（2） bt（2） Bs0（3）、δ（3） αp（4）hm（2）bt（2）Bs0（1）、δ（4） αp（1） hm（1） bt（2） Bs0（2）。通过方差分析，优化因子δ、bt、Bs0的选取以效率最大为标准，αp的选取以齿槽转矩最小为标准，hm的选取以单位永磁体产生的转矩最大为标准。因此，选取δ（4） αp（4） hm（1） bt（2） Bs0（3）为最佳组合。优化后电机的主要参数如表7所示。

3 优化及仿真结果分析

本文以一台分数槽集中绕组永磁同步电动机作为研究对象，对电机的气隙长度、极弧系数、永磁体厚度、定子齿宽及定子槽口宽度进行优化。电机2维模型如图3所示。

3.1 优化结果分析

根据表7的最终优化方案，建立电机仿真模型，电机优化前后性能指标对比如表8所示。根据表8计算可知，优化前后，电机效率增加了0.31%，电机齿槽转矩降低了30%，单位质量永磁体产生的转矩增加了50.02%，优化效果较明显。

3.2 有限元仿真结果分析

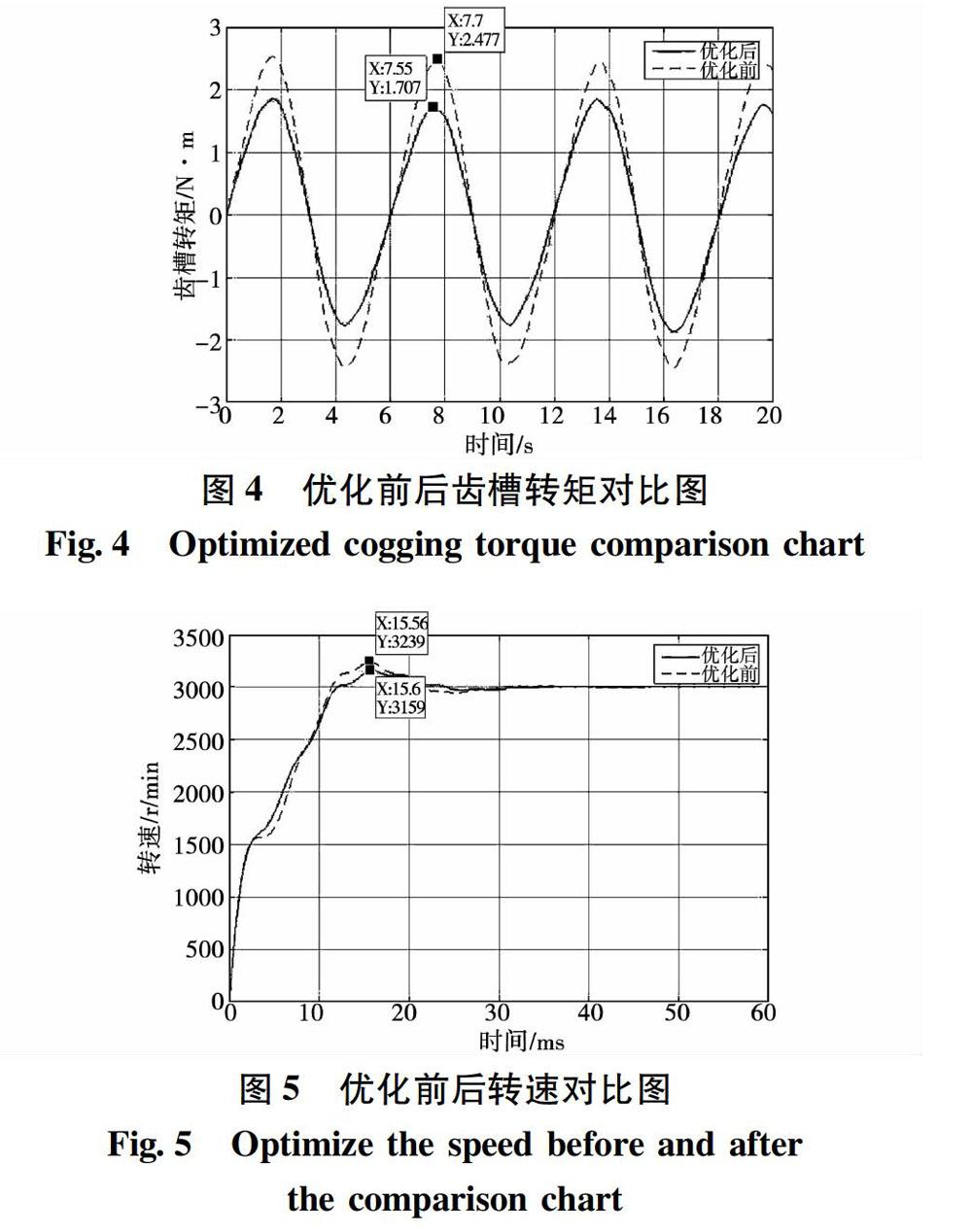
为了验证优化方案的可行性，利用有限元仿真软件对优化前后电机进行二维瞬态场分析，得到的仿真结果如图4、图5和图6所示，其中图4为优化前后电机齿槽转矩随时间变化的曲线，图5、图6分别为优化前后电机转速、转矩与时间的曲线。

从图4可以看出，优化前电机齿槽转矩为2.477N·m，优化后电机齿槽转矩为1.707N·m，电机齿槽转矩减少了31%。从图5可以看出，优化前电机转速峰值为3239r/min，优化后电机转速峰值为3159r/min;从图6可以看出优化前电机转矩峰值为277.1N·m，优化后电机转矩峰值为232.8N·m，优化前后电机转矩与转速波动幅值明显减少。通过有限元分析验证了该优化方案的可行性。

4 结 论

本文提出了一种基于田口方法的优化方法。以气隙、极弧系数、永磁体厚度、定子齿宽和槽口宽度作为优化变量，电机效率、齿槽转矩、单位永磁体产生的转矩为优化目标对分数槽集中绕组永磁同步电动机进行优化。借助有限元方法，对优化后的电机进行二维瞬态电磁场分析，通过实验及有限元分析可得如下结论：

1）根据方差分析可知，定子槽口宽对电机效率影响最大，永磁体厚度和定子槽口宽对电机齿槽转矩影响最大，永磁体厚度对单位质量永磁体产生的转矩影响最大;

2）利用田口方法对电机进行优化，能有效的抑制电机的齿槽转矩，提高电机效率，降低转矩及转速波动;

3）通过有限元分析，验证了优化方案的可行性。

综上所述，田口方法能有效的提高电机的性能，且适用于分数槽集中绕组永磁同步电动机的优化设计。虽然本文未优化其他复杂转子磁路的分数槽集中绕组永磁同步电动机，但是在实际应用中仍然具有一定的理论指导作用，为新型分数槽集中绕组永磁同步电动机优化等方面的深入研究奠定了基础。

参 考 文 献：

[1] 王艾萌， 温云.田口法在内置式永磁同步电机优化设中的应用[J].华北电力大学学报，2016，43（3）：39.

[2] 唐任远.现代永磁电机理论与设计[M].北京：机械工业出版社，1997：161.

[3] 贾金信，杨向宇，曹江华.基于田口法的内嵌式永磁电动机的优化设计[J].微电机，2013，46（6）：1.

[4] 陈俊峰.永磁电机[M].北京：机械工业出版社，1982.11.

[5] 王秀和.永磁电机[M].北京：中国电力出版社，2007：7.

[6] FAIZ J， KEYVANI-Boroujeni B. Optimal Design of Internal Permanent Magnet Motor for Starter/Generator of Hybrid Electric Vehicle[C]//Power Electronics and Motion Control Conference， 2006. Epe-Pemc 2006. International， IEEE， 2006：984.

[7] 李立毅，唐勇斌，刘家曦，等.多种群遗传算法在无铁心永磁直线同步电机优化设计中的应用[J].中国电机工程学报，2013，33（15）：69.

[8] 谢颖，李吉兴，杨忠学，等.改进遗传蚁群算法及其在电机结构优化中的研究[J].电机与控制学报，2015，19（10）：64.

[9] 郭亮，卢琴芬，叶云岳.基于粒子群算法的直线振动发电机优化设计[J].电机与控制学报，2008，12（4）：442.

[10]KIM S I， LEE J Y， KIM Y K， et al. Optimization for Reduction of Torque Ripple in Interior Permanent Magnet Motor by Using the Taguchi Method[J]. IEEE Transactions on Magnetics， 2005， 41（5）：1796.

[11]LEE S，KIM K，CHO S，et al.Optimal Design of Interior Permanent Magnet Synchronous Motor Considering the Manufacturing Tolerances Using Taguchi Robust Design[J].Iet Electric Power Applications，2014，8（1）：23.

[12]STPHANE Brisset， FRDRIC Gillon， STPHANE Vivier，et al.Optimization with Experimental Design： An Approach Using Taguchis Methodology and Finite Element Simulations[J].IEEE Transactions on Magnetics，2001，37（5）：3530.

[13]LOW T S， CHEN S， GAO X. Robust Torque Optimization for BLDC Spindle Motors[J]. Industrial Electronics IEEE Transactions on， 2001， 48（3）：656.

[14]SONG J，DONG F，ZHAO J，et al. Optimal Design of Permanent Magnet Linear Synchronous Motors Based on Taguchi Method[J].Iet Electric Power Applications，2017，11（1）：41.

[15]TSAI W C. Robust Design of a 5MW Permanent Magnet Synchronous Generator Using Taguchi Method[C]// International Conference on Computing and Convergence Technology. IEEE， 2013：1328.

[16]NAL Kurt， NBILGIN G. Design and Optimization of Axial Flux Permanent Magnet Synchronous Machines Using Taguchi Approach[C]//International Conference on Electrical and Electronics Engineering. IEEE， 2009（1）：202.

[17]高泽梅，王淑红，武潇，等.基于田口实验的永磁同步电动机优化设计[J].微电机，2015，48（1）：16.

[18]ZHAO Baojiang，LI Shiyong.Ant Colony Optimization Algorithm and Its Application to Neuro-Fuzzy Controller Design[J].BIAI Transactions on Systerms Engineering and Electronics，2007，18（3）：603.

[19]邱清盈.穩健设计进程策略的研究及实践[D].杭州：浙江大学，2003：28.

[20]高泽梅.内嵌式永磁同步电动机优化设计及特性分析[D].太原：太原理工大学，2016：39.

（编辑：温泽宇）