实践波利亚的“怎样解题表”，培养学生反思性学习的能力

张瑶

【摘要】解题研究是沟通数学理论与实践研究的桥梁，是数学教学和学习的永恒主题，深受广大教师和学生的关注.然而解题思维具有动态、内隐等特征，借助波利亚的“怎样解题表”将解题程序和自我调节的监控系统有机结合，使解题活动成为有目标、有方法的主动行为.通过对解题思维过程的内省，培养学生反思性学习和创造性活动的能力.

【关键词】“怎样解题表”;反思性学习;解题研究

一、问题的提出

反思性学习是应课程改革而产生的一种崭新的学习方式，是“学会学习”的突破口，是适应人的终身发展需要的重要学习方式.反思性数学学习是指通过对数学学习活动过程的反思来进行数学学习的一种有效学习方式[1].它是对已完成的思维过程进行周密且有批判性的再思考，以求得新的深入认识，或提出疑问，作为新的思考起点的一种数学学习方式[2].然而不论是从上一轮小课题对学生自我反思维度的调查结果来看，还是从教学实际本身考虑，反思性数学学习都是较为薄弱的环节.面对这一现实问题，笔者试图从解题教学这一深受广大教师关注，符合学生学习心理，较易入手的方式作为突破口，借助波利亚的“怎样解题表”将解题思维过程外显化，使学生的数学解题活动成为有目标、有方法的主动行为，增强学生的解题能力，并通过对解题思维过程的内省，提高思维的创造性，进而培养学生反思性学习的能力.

二、波利亚和他的“怎样解题表”

乔治·波利亚（Geoge Polya，1887—1985），美籍匈牙利数学家、数学方法论大师，对数学思想的理解与解题方法的归纳形成了自己独特的数学教育思想，尤其是他的著作《怎样解题》一书更堪称解题教学的经典之作，被数学教育工作者广泛应用于教学研究[3].

波利亚通过自己数十年的教学与科研经验，致力于探索解题过程的一般规律，具体表现在他的“怎样解题表”上.它把解题过程概括为四个阶段：弄清题意、拟订方案、执行方案、回顾.这四个阶段并不是彼此孤立的，而是一个四步骤的宏观解题程序，其中“弄清题意”是认识问题、并对问题进行表征的过程，它是成功解题的必要前提;“拟订方案”需要反复思考探索，把握住题目的核心和解题关键，寻找快捷有效地解题思路;“执行方案”则需要认真贯彻落实拟定的方案，且不断解决在解题实际过程中遇到的意料之外的难题;“回顾”是解题过程中最容易被忽视的一个环节，是不断总结和反思的环节，也是引导学生不斷进步的重要环节，波利亚也将回顾视为解题的必要环节[4].这四个步骤不但能促成解题思路的形成，提高解题成功的可能性，还能诱发数学灵感，形成好的念头，更重要的是他将自我调节的监控系统植入解题过程中，是进行反思性学习的良好契机.

三、实践波利亚“怎样解题表”的教学片段

为了使大家对“怎样解题表”的实践过程有更直观的感受和深刻的理解，笔者节选了教学案例的部分实践过程，以期更好地分享“怎样解题表”教学实践成果.下面是在解题教学中实践波利亚的“怎样解题表”的教学片段，以期边实践，边反思，边调整，边完善.

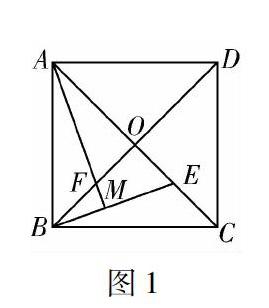
题目：已知正方形ABCD的对角线AC，BD相交于点O，E是AC上一点，连接EB，过点A作AM⊥BE，垂足为M，AM交BD于点F.求证：OE=OF.

（一）弄清题意

师：这是一个什么问题？

生：这是一个平面几何的证明题.

师：已知条件是什么？把条件的各个部分分开，你能否把它说出来？

生：已知条件有四个：① 四边形ABCD是正方形;② AC，BD是其对角线，并相交于点O;③ E是AC上一点;④ 连接EB，过点A作AM⊥BE，垂足为M，AM交BD于点F.

师：要求证什么？

生：要求证两段线段OE，OF相等.

师：满足条件是否可能？

生：显然满足条件是可能的，只是对条件③E是AC上一点还有些不明确，AC是指线段还是直线，如果条件③确定，那么条件④也就确定了.

师：若假设题目中没有给出图形，条件③明确为E是线段AC上一点，你会把E点画在哪呢？

生：E点有可能在AO之间，也有可能在OC之间（也就是本题图中给出的位置），E点也有可能就在O点处.

师：根据上述考虑能按E点的不同位置画出图形吗？

生：能，应该是三种情况分别画出三种图形.

生：可是正方形是轴对称图形，它的两条对角线也是它的对称轴，根据对称性E点在AO之间与E点在OC之间应属于同种情形.对E点在O点处，点E，O，F，M四点重合，显然OE=OF是成立的.因此，我们只需研究题中图形即可.

师：很好！我们找到了这道题的一般图形和它的一个特例.回到题中给出的图形，要确定未知，所给条件是否充分？或者它是否不充分？或者是多余的？或者是矛盾的？

生：条件感觉是充分的，但不是十分确定.

师：好，让我们继续往下走.

（二）拟订方案

师：要证明两条线段相等，你能想到哪些方法呢？

生：全等三角形的性质，等腰三角形的性质，线段中垂线的性质等.

师：这道题应该从哪个方法入手呢？

生：全等三角形.

师：为得到线段OE，OF相等，我们需证哪对三角形全等呢？

生：△BOE和△AOF.

师：用红笔将这两个三角形勾画出来，你能找到证明这对三角形全等的条件吗？

生：首先这两个三角形都是直角三角形，有直角相等的条件.

生：根据正方形的性质又可以得到OA=OB.

师：仅凭上述两个条件能证明△BOE≌△AOF吗？

生：不能，还需一个边的条件或一个角的条件.

师：能找到这个条件吗？

生：（沉默）

师：回到题目中看看条件都用完了吗？或者图形中还有隐含条件吗？或者联想一下，你以前做过与这道题相像的题目吗？

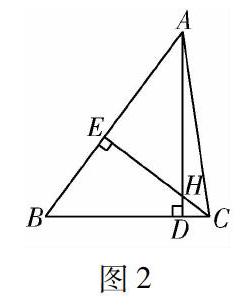
生：我记得在学直角三角形全等时曾经做过一道题，与此题有点像.题目是这样的：在△ABC中已知EH=EB，AD⊥BC，CE⊥AB，垂足分别为D，E，AD，CE交于点H，求证△BEC≌△AEH.

师：还记得当时是怎么证明的吗？

生：∠AEH=∠BEC=90°，EH=EB这两个条件是显然的，对，还利用了图中的隐含条件∠AHE=∠DHC（对顶角相等）从而得到∠EAH=∠ECB（等角的余角相等）.

生：找到了，我们现在这道题也可以用图中的隐含条件，从而得到∠OBE=∠OAF，利用角边角条件可以证明△BOE≌△AOF，从而得到OE=OF.

（三）执行方案

师：太好了，详细说出你求证的过程，并尝试找到每一步的几何依据.

（有了上述分析过程，具体解题步骤略）

（四）回顾

师：这道题的证明都用到了哪些知识？

生：正方形的性质，垂直的定义，等角的余角相等，判断三角形全等的条件，全等三角形的性质等.

师：你还有其他的方法证明吗？

生：还可以用角角边条件证明那两个三角形全等.

师：你能不能仅从图中一下子看出要证明的结论来.

生：E，F可看作正方形对角线AC，BD上的两个动点，F点跟随E点的运动变化而变化.

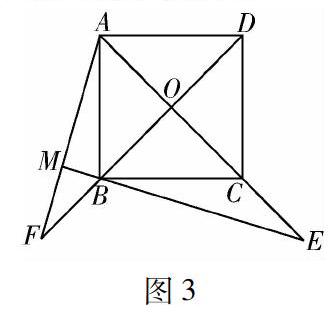
师：回到先前的问题，若条件③E是直线AC上一点，结论会有变化吗？画图看看.

生：E点不论在AC的延长线上还是反向延长线上，结论不变，证明的方法也相同.

师：整理你的思路，总结解题所用的思想方法.

四、“怎样解题表”实践运用中值得注意的问题

首先，教学实践表明波利亚的“怎样解题表”是指导学生准确掌握解决数学问题的行动指南，学生只有依照科学的数学理论，反复训练提高，才能不断有效提高分析数学问题、解决数学问题的能力，并逐渐形成科学有效的数学思维习惯[5].

其次，波利亚在他的解题理论著作中给出了很多提示语，这些提示语能引导学生的思维方向.而且这些提示语是在数学问题中自然而然形成的，具有一般性和常识性的特点，符合学生的数学思维习惯和思维方式，这就要求教师不仅要善于提炼提示语，更要进一步引导学生逐渐学会提炼学生自己的提示语.

再次，波利亚解题表中的大量提示语是针对主体自身思维活动的反诘，自我监察、自我预测、自我调节.在解题教学中应注重训练学生将这些提示语内化为自己的一种解题习惯，久而久之形成适合自己的解题程序.

最后，波利亚的解题理论及“怎样解题表”毕竟是从国外引进的，我们应结合学生的实际将其本土化，使其更好的运用于我们的数学教学.

五、波利亚“怎样解题表”对培养学生反思性学习能力的几点思考

（一）弄清问题，加强对理解题意的反思

在培养学生反思性学习能力的实践中，学生的个体差异主要集中表现在理解题意时自我反思的能力差异上，从而导致对题意的理解不准确、不全面.教师在培养学生反思性学习能力时，应注重从以下几个方面着手，理解题意是否有偏差？能否以恰当的形式描述题目中的条件？能否对题目进行符号表征？对问题含义的设问是否清楚？有关对象即概念、性质、方法的意义是否清晰？所用概念、定理的条件是否正确？对相近对象的异同是否认识清楚？

（二）拟订方案，实施方案，加强对解题思维策略的反思

學生解题思维策略的选取，直接影响了“怎样解题表”实践运用的实际效果.解题思维策略的反思可从以下几个角度考虑：看到题目后最初的想法？走过哪些弯路？为什么原先的思路行不通？有什么规律性的经验可以吸取？我的思考与教师、同学的思考有什么不同？中途是否做过某些预测和调节？这些调节对自己的思考是否起到作用[5]？

（三）回顾，加强对解题结果的反思

做好“怎样解题表”实践运用过程中解题结果的反思，对培养学生缜密的思维，诱发数学灵感及培养反思性学习能力都有很好的促进作用.作为教师一定要特别注重引导学生加强对解题结果的反思.具体讲我们可以从探讨解法、挖掘规律、引申结论等方面思考[6].

从探讨解法的角度反思：能否利用不同的知识，通过不同的途径求得问题的解？通过对不同解法的比较，能否找到更满意的解法？是否有更一般的方法？是否有更特殊的方法？这些方法各有什么特征？

从挖掘规律角度的反思：这个问题能否导出一些有用的东西？这个结果或解法能否用于解决其他问题？我们的方法是否有需要改进的地方[6]？

从引申结论的角度反思：结论合理吗？有没有反例？结论可以一般化吗？可以推广吗？可以引申吗？是否有变式问题？解题关键在哪里？

总之，“怎样解题表”对培养学生反思性学习能力有较好帮助，最终这种帮助会体现在学生的数学思维方面，只有从锻炼思维的角度来看待数学学习，才会真正关注想法中深层次的东西，关注思维的深度与高度，从而自觉形成反思性学习的能力.笔者主要在教学实践过程中，借助波利亚的“怎样解题表”对培养学生反思性学习能力进行了一些有益尝试和探索，取得的成果是基于教学过程中所涉及的学生.在不同的地区、不同的学校，学生具有不同的背景和特点，需要广大教师认真分析掌握学生的特殊情况，掌握一些必要的增强反思能力的教学策略，才能有针对性的运用好“怎样解题表”，真正发挥其实效性.

【参考文献】

[1]郑菊萍.反思性学习简论[J].上海教育科研，2002（8）：43-45.

[2]赵玉香.反思性学习理论与实践探索[M].济南：山东大学出版社，2006：108.

[3]梁红娥.波利亚的数学解题思想及其在中学数学教学中的应用[D].呼和浩特：内蒙古师范大学，2005.

[4]G·波利亚著.怎样解题[M].涂泓，冯承天，译.上海：上海科技教育出版社，2002.

[5]唐剑琴.利用波利亚“怎样解题表”提高习题教学价值[J].新课程，2015（7）：23

[6]罗增儒，罗新兵.波利亚的怎样解题表[J].中学数学教学参考教师版，2004（4）：23-25.