关于Courant-Friedrichs的跨音速激波问题
2019-01-12辛周平
辛周平
(香港中文大学数学科学研究所,香港 新界 沙田)
1 引言
理想的可压缩流体是由非常复杂的欧拉方程来描述的.当流动和时间无关时(定常流),下面的定常欧拉方程组[1-4]

分别表述了流体的质量守恒,动量守恒和能量守恒.其中ρ∈R1是密度,Rn是速度场,

是压力,

是总压力,e=e(ρ,s)是内能,s是熵,是声速,而p,e,s,ρ之间的关系由流体状态方程确定.
相对于非定常欧拉方程组[1,3],(1)是较为简单的,因而也成为人们最先尝试解决的重要模型.但事实上,(1)具有许多特性使得其研究变得极为困难.首先和非定常情形类似,由(1)确定的波的传播也是依赖于波的本身,所以(1)的解一般是有激波的[1-2].其次,对很多有意义的波形,(1)都是混合型或变形,且常有退化情形(音速元)的出现,这使得即使是局部求解都变得相当困难和复杂.因此关于方程组(1)的一般边值问题的理论是完全公开的[2,4-5].
由于(1)的复杂性,历史上人们研究了一些简化模型,其中最为广泛研究的模型是位势流方程[2,4,6],即假定熵为常数且无旋,则p=p(ρ)且存在一个速度位势函数ϕ使得u=∇ϕ,而φ满足下述位势流方程:

其中


此时,(3)的特征值是

因此(3)在超音速区域是严格双曲的,但在亚音速区域是椭园-双曲耦合的,而当流体通过音速元是变形的且具有严重退化.相对于位势流方程,(3)更具挑战性,因为即使在亚音速区域,它也是混合型的,这对问题的求解提出了很大的困难.
尽管(1)(或(2)或(3))有着重要的理论和实际应用意义,对其的理论研究也取得了一系列重要进展[1-86],但一般性的数学理论还远远没有建立.过去的研究主要集中在具有较强实际应用背景的一些重要问题的实验,数值及理论研究:绕流和管道流问题.定常可压缩绕流问题,包含著名的飞机机翼的空气流动和音障问题,在空气动力学和航天航空中有重大意义,是大家一直关心的一个问题并且有着广泛的研究结果,特别是位势流的情形.
关于光滑亚音速绕流及超音速含有激波的流动都有了丰富的结果[2,4,8,11-14,18-21,29,41-42],甚至最近也有了一些有意思的亚音速-音速位势流的结果[9,22,43].但光滑跨音速绕流的研究非常具有挑战性,因为Morawetz教授证明了光滑跨音速绕流一般是不稳定的[23],而跨音速激波是不可避免的,但这类解的存在性研究基本上是个空白.另一类重要的问题是管道中的定常可压流.这类问题的研究不仅具有重要的实际应用意义,而由于几何形状的效应使得在弯曲管道中的定常可压缩流体具有更丰富的现象和动力学行为[44-45].这一问题的数学理论最近也取得了一系列重要进展,特别是一般弯曲管道中的光滑无旋亚音速流的存在性及对质量通量的依赖性,无旋亚音速-音速流的存在性,包括有旋时的推广等都取得了一系列较为深刻的结果[15-16,26,30,32,34-40,46-52].特别是文献[37]得到了对一大类二维弯曲有限管道中满足物理边界条件的李普希茨连续的无旋亚音速-音速流的存在性,并对音速元的位置给出了精确的刻划.而文献[35]第一次给出了一类二维De Laval管道中满足物理边界条件的Meyer型光滑无旋跨音速流的存在性.但像绕流问题一样,当管道中流体的质量通量超越临界值时,流体一定是跨音速的,而且正如Morawetz指出的,光滑的Taylor型跨音速流一般都是不稳定的[23],从而使跨音速激波的出现变成了一个不可回避的问题.
但含有激波的跨音速流的研究极为困难,是非线性偏微分方程研究中的巨大挑战之一,因为这样的波形通常都要涉及自由边界,退化,变形,混合型方程,复杂的波的相互作用,复杂或不正则的边界条件等困难.因此,只是在拟一维时取得了一些深刻的结果[53-55].而在高维,尽管应用补偿列紧框架做了一系列有益尝试,一个系统的理论还有待建立,已有的结果大部分集中在满足某些特殊边界条件的跨音速激波的适定性[4,7,17,31,55-67].因此,研究弯曲管道中满足物理边界条件的跨音速激波的适定性具有重要的意义,而在有限光滑收缩-伸张管道(称为De Laval管道)中的跨音速激波的研究就是在工程应用和数学理论中都极具意义的问题.
基于众多的工程实验,Courant-Friedrichs在其1948年的专著中提出了下面的关于 De Laval管道中的跨音速激波问题[1](如图1所示):

图1 De Laval管道中的跨音速激波
考虑进入一个De Laval管道的一致超音速流.对于给定的在适当区域的出口压力Pe,若超音速从收缩区到管道脖子保持光滑,则在管道的伸张部分某处一定会产生一个激波,通过激波后流体被压缩并变慢成为亚音速流动,而激波的位置和强度会自动调整从而达到给定的出口压力Pe.
这个问题的正向结论和工程实验非常吻合,而在拟一维时也很容易证明[44,53-54],特别是Courant-Friedrichs在管道是部分张开的圆锥时可以给出严格的解[1].对于某些适当修改的边界条件或其它额外条件,管道中的跨音速激波存在性也有了许多进展[7,17,55-56,58-62,64-65].但对Courant-Friedrichs问题在一般情形还远远没有解决.这里的主要困难在于这是一个极为复杂的混合型方程的自由边值问题,它即使在亚音速区也不是椭圆型的(而是双曲-椭圆耦合的),而且在出口的给定压力边界条件是完全非平凡的.另外,激波同管道边界的碰撞会导致低正则性从而使问题的分析变得困难.下面会对该问题的近期进展做一个综合性的描述.
2 二维 Courant-Friedrichs的跨音速激波问题
本节给出Courant-Friedrichs的跨音速激波问题的精确描述(见图2所示).为简单起见,假定管道为

其中fi是光滑的(i=1,2),a和b是给定常数.

图2 Courant-Friedrichs的跨音速激波
设给定的出口压力为p=pe(x2),它是一正的光滑函数.考虑一个密度为常数ρ0,熵为常数s0,速度场为(q0,0)的一致超音速流(q0>c(ρ0)为常数)进入该管道.设寻找的激波曲线为

则过Σ的R-H跳跃条件是

这里

表示A在的跳跃.将管道区域分为左区域Ω−和右区域Ω+,则

定义


管道壁假定是实的,则

来流条件是

出口边界条件为:

则二维Courant-Friedrich的跨音速激波问题可表述为:
目标在适当条件下寻找二维定常可压缩欧拉方程组(1)的在Ω上的分片光滑解,使得解在Ω−上超音速,在Ω+为亚音速,并满足条件(6),(8)-(11).
注意到这里来流要求是一致流只是为了简化,来流是变量时的描述是类似的.当然三维的情形也可以进行类似的描述.
3 主要进展
尽管这个问题在理论和应用都极为重要,但由于上述的困难,理论研究的进展较为缓慢.上个世纪的主要结果大多数集中在一维或拟一维情形.从这个世纪初开始,一系列的高维成果开始涌现,下面列举其中一些结果.
首先,一个令人惊奇的结果是对于常见的位势流模型(2),Courant-Friedrichs的跨音速激波流问题的答案一般是负面的[55,64].事实上,对位势流方程(2),文献[64]中构造了一类De Laval管道,使得Courant-Friedrichs问题或者不存在,或者解存在但不唯一,或者解不连续依赖于边界值,只有对特殊的出口压力条件,该问题的解才具有适定性[55],导致对位势流该问题的不适定性主要在于对(2)来讲,给定出口压力条件在亚音速区是一个非线性斜导数边界条件,从而引起了椭圆问题的不相容性.但对于修正的位势流方程(即假定熵是未知变量且流体无旋),则该问题是有可能适定的[7].因此为了研究Courant-Friedrichs管道中的跨音速激波问题,人们的注意力主要集中在有旋的欧拉方程.而此时,该问题的困难和熵是否是常数无关.
其次,注意在Courant-Friedrichs的管道中的跨音速激波问题中,激波的位置是一个自由边界,应该由管道的几何形状,来流和出口压力条件唯一确定.若激波被要求通过一给定点,这时该问题解的唯一性则可以被证明[58-62,65].但存在性一般是不成立的.若允许出口压力相差一个未知常数,则解的适定性对一类管道可以建立(见文献[58-60,66-67]).
对于一般情况下(不附加额外条件)该问题的适定性结果是关于二维Courant-Friedrichs的跨音速激波的结构稳定性的一系列工作[68-73].当出口压力是常数而管道为张开的直管道时,Courant-Friedrichs通过解决常微分方程的自由边界问题给出了该问题的存在唯一性[1].而Courant-Friedrichs解的结构稳定性是该问题最有意义的研究课题之一.在文献[68-73]中,作者首先证明了对于一般二维De Laval管道,若它的伸张部分是张开直管道的任意小摄动,当出口压力函数是常压力的小摄动,则Courant-Friedrichs的跨音速激波问题的解是唯一确定的,而且出口压力的变化区域也可以确定.进一步,若管道的伸张部分是变化较为平缓而来流的马赫较大,则该解的激波位置单调依赖于出口压力.这些结果对来流是一致流的小摄动也是对的(见翁尚昆的博士论文).这些结论的确切描述会在下面给出.因此,Courant-Friedrichs的跨音速解是结构稳定的.这些结果也可推广到三维轴对称管道.注意到对于拟一维问题,一个著名的结果是在管道张开部分中的跨音速激波实际是动力学稳定的,而在管道中的收缩部分的跨音速是不稳定的[45],这个结果的证明依据Glimm方法[45,54].但对于分片光滑摄动,在张开管道中的跨音速激波的动力学稳定性可以用新的能量和谱分析去证明并可得到衰减率[65,74].
需要指出的是,上述Courant-Friedrichs的跨音速激波的结构稳定性证明的关键是用管道的几何和出口压力的关联来确定激波的可能通过的管道壁上的位置,而这又严重依赖于背景管道是张开的直管道.因此这个方法对一般管道是不适用的.最近,文献[75]中给出了一个在一般平缓管道由出口压力和管道几何确定激波通过管道壁位置的一个新方法,从而得到了Courant-Friedrichs的管道中跨音速激波问题的解的存在性.
4 Courant-Friedrichs的跨音速激波的结构稳定性和分析方法
本节将陈述关于Courant-Friedrichs的跨音速激波结构稳定性的主要结果及其证明的主要思路.这些都是文献[68-73]中的结果的一个摘要.这就给出了对一类张口部分是一个张开的直管道的小的任意摄动的De Laval管道时,Courant-Friedrichs的跨音速激波问题有一个确定的正面答案.
在极坐标

意义下,要考虑的二维De Laval管道如图3所示:

图3 二维De Laval管道
这里假定上下管道壁分别为

且 Γ1和 Γ2都是C3,α光滑(0<α<1).其中和形成管道的收缩部分,而组成管道的伸张部分,这里x0>1是个给定的数.
设,对于i=1,2,

其中

而出口压力条件可表述为:

这里pe是个正常数,而

其中c是任意给定常数.在(13)和(14)中,ε是非负参数.注意到当ε=0,伸张部分的管道壁变成直的,即,而出口压力变成常压力pe,这时 Courant-Friedrichs[1]已证明了存在正常数pm和pM,满足pm 而激波位置由r=r0确定.这里,定义在超音速区上而且在r=x0附近关于θ=0对称,同时在亚音速区 这节的主要结果是Courant-Friedrichs构造的这个背景解是结构稳定的. 定理4.1[73]假定管道由(12)和(13)确定(如图3所示),则存在一正常数ε0使得对所有ε∈[0,ε0],Courant-Friedrichs的管道中的跨音速激波问题,(1)(6)(8)(9)(10)(这里x1=a换为r=x0−1) 和(11),有唯一的解,且具有如下性质: 这里Ω+是亚音速区,即 而 注释1这个结果证明了Courant-Friedrichs的跨音速激波解在对管道形状和出口压力的一般小摄动的结构稳定性.这个稳定性结果可推广到来流是一致流的小摄动的情形(见翁尚昆博士论文),从而也给出了二维完全欧拉方程的Courant-Friedrichds的跨音速激波问题对一类重要De Laval管道的第一个完全正面答案. 注释2对一般的 De Laval管道,定理4.1中的跨音速激波解在亚音速区的正则性都是最优的,即使管道是C∞正则,0<α<1也是无法改进的[15],但若管道是直的,即fi(r)≡0,这时管道壁伸张部分可表示为: 则解的正则性可提高到C2,α或者更高.事实上,我们有下述结果: 定理4.2[68]设定理4.1的假定成立,且将(12)改成(21),则存在正常数ε0使得对所有的ε∈[0,ε0],Courant-Friedrichs的管道中的跨音速激波问题有唯一解,而且满足以下性质: 其中 注释3当管道壁的张开部分是直的时候,激波和管道壁具有较高的匹配性[15,68],这就导致了定理4.2的正则性高于定理4.1中的正则性.但对一般弯曲管道(即使无穷光滑),定理4.1的正则性是最佳的[15]. 注释4注意到在上述两个定理中,对θ0没有小性要求,也就是说没有要求管道是水平管道的小摄动(这是以前很多文献中的主要要求之一).但若θ0较小,会得到下述关于跨音速激波单调依赖于出口压力的重要结论. 定理4.3[69]设定理4.2的假定成立,则存在一个适当小的正常数使得若 并且 这里M−(x0)是马赫数,是常数,则 Courant-Friedrichds的管道跨音速激波问题有唯一的解,且具有以下性质: (iii)跨音速激波的位置x1=ξ(x2)是单调和Lipschitz连续地依赖于出口压力. 注释5这里指出证明定理4.1的主要困难.用特征线方法得到上游光滑超音速流是容易的,所以Courant-Friedrichs的管道中的跨音速激波问题可归结为寻找亚音速区域而且满足给定的边界条件和穿过激波的跳跃条件.因为激波位置是未知的,这就变成了一个带有固定边值的双曲-椭圆耦合方程的非线性自由边界问题.注意到越过激波的跳跃条件给出了关于激波位置的一个常微分方程组.因此要确定激波的位置就需要激波过某点,比如激波和管道壁的交点的位置.在已有的许多工作中,假定这个点是给定的,但一般来讲,这时的Courant-Friedrichds的管道中的跨音速激波问题是超定的[63],只有在允许出口压力确定到一个常数或特殊的压力条件,解才可以适定[55,58-60].因此,激波位置的确定(即使是其上一个点)是和满足固定边界的下游亚音速流动同时进行的.这是解决该问题的关键点之一.另外一个最重要的困难是解在亚音速区的低正则性.在文献[63]中,作者证明了由于激波和管道壁相交,只有在交点附近Hölder连续的亚音速流可以存在除非管道壁是直的.但在亚音速区,欧拉方程组(1)是一个椭圆-双曲耦合方程组,因之在亚音速区解的低正则性导致非线性问题的很大困难. 注释6定理4.1证明的主要步骤可概括如下: 第一步,通过特征线方法,可以找到满足管道壁和入口条件的上游光滑超音速流. 第二步,将跨音速激波归化为亚音速欧拉方程的非线性自由边界和固定边值问题. 第三步,通过Euler-Lagrange变换将该自由边界问题变成一个在固定区域求解下述系统边值问题: ·关于激波位置的带有自由初始值的非线性常微分方程; ·关于压力和角速度的一个非线性一阶椭圆组; ·分别关于熵和Bernoulli函数的输运方程. 注意到Euler-Lagrange变换只是一个部分速度图变换,因之出口压力条件会变成对上述系统的一个非局部边界条件. 第四步,求解上述系统的初边值问题.这是通过设计一个能够有效分离双曲变量和椭圆变量的迭代格式来实现同时确定跨音速激波的位置和下游的亚音速流动.这个迭代格式的关键是求解一个含低正则非局部项(超音速来流和下游亚音速流在激波的相互作用)和一个自由参数(激波和管道交点的位置)的一阶椭圆组的混合边值问题.这个问题的可解性条件正好给出了激波和管道壁交点的位置,从而解跳跃条件可确定激波的位置. 第五步是推导迭代解的紧性估计. 最后可证明解的存在唯一性和相关性质. 注释7所有二维的结果都可以推广到三维轴对称的情形[70-72].当有场的作用时(比如自重力场或电力场),已有很多有意义的推广[76-79]. 尽管有了上述进展,Courant-Friedrichds的管道中的跨音速激波问题在很多有意义的情形还没有解决,特别是三维一般管道或非常数出口压力,有着实质上的困难,但具有重要物理和理论意义. 1.即使对于二维问题,由于第4节中的结果强烈依赖于背景解(即Courant-Friedrichds的跨音速解)的结构.因此当管道是一般的De Laval管时,Courant-Friedrichds的管道中的跨音速激波问题是公开的,只有当管道是平行直管道的小摄动时,文献[75]给出了一个存在性结果.一般情形还是未知的. 2.更重要的是三维问题.只有当管道,来流和出口压力都是轴对称时,才有类似于第4节中的结果[70-72].对一般情形,Courant-Friedrichds的管道中的跨音速流问题完全公开.注意到第4节中的结果完全依赖于二维结构,是不适用于三维情形.需要新的想法和技术.但注意到当管道为伸开的直锥时,这个问题解的唯一性已在文献[72]证明,但存在性还没有证明.但在这种情况下,亚音速区的高正则性是可期待的,因此存在性也是可期待的.












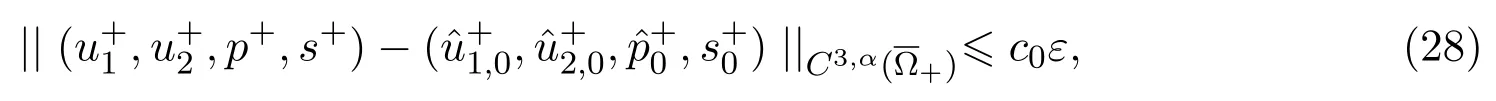
5 公开问题
