带交叉扩散与自扩散项的捕食-食饵模型正解的局部分歧

容跃堂

(西安工程大学理学院,陕西 西安 710048)

1 引言

用建立微分方程模型的方法来研究生物数学中物种的动力学行为已经非常普遍,并且学者们在这方面的研究也得到了许多不错的成果[1-7].文献 [1]中,作者提出并研究了如下的Variable-Territory捕食-食饵模型:

这里,关于模型(1)的生物学意义可参考文献[2-3].

由于实际上物种在空间分布上是不均匀的,且这一因素很可能会影响系统的生态动力学行为,因此文献[4]在上述模型基础上考虑了扩散项,研究了模型:在Dirichlet边值条件下的平衡正解的存在性及稳定性.

考虑到种群间的相互影响在种群扩散中所起到的重要作用,文献[8]在模型(2)的基础上再研究带有交叉扩散项的情形,即模型

在交叉扩散项影响下的局部分歧.模型中,Ω为有界开区域,Ω⊂Rn,且边界光滑,食饵和捕食者的种群密度分别是u,v,参数a,b,c,d,α,β均为正常数.

本文讨论在交叉扩散和自扩散项影响下的局部分歧.讨论模型

对应的平衡态方程为:

取

由于

因而(u,v)≥0与(U,V)≥0之间一一对应.下面主要研究模型(5)的等价半线性椭圆系统:

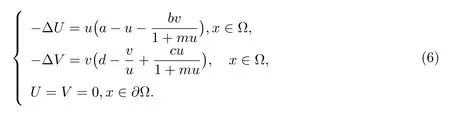
那么X也为Banach空间,

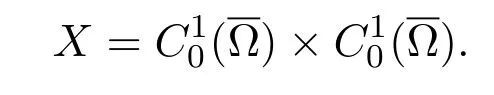
那么由文献[9]知,问题(7)的特征值λ1(p,q)是简单函数,且满足

同时还有ϕ1,ϕ2,···是它们的对应特征函数.此外,λ1(p,q)随p和q(x)的递增而递增,即λ1(p,q)是严格单调递增函数.这里取λi(1,q)为λi(q),且

讨论边值问题

2 解的估计

引理2.1[9]如果a≤λ1,则u=0是问题(8)的唯一非负解,若a>λ1,那么问题(8)有唯一正解为θa.即当a>λ1时,问题(5)有半平凡解(θa,0);若a≤λ1,问题(5)不存在正解.若a>λ1,则问题(6)有半平凡解,此处

定理2.1假如a>λ1,问题(6)有任意正解(U,V),那么∀x∈Ω,

证明若∃x0∈Ω,满足

且

故

同理可得,若∃x1∈Ω,满足

则得

因此,

又(u,v)与(U,V)一一对应,因此定理得证.

3 解的分歧

引理3.1[10]取

若a>λ1,则L(a)可逆.

引理3.2[11]假如d>λ1,同时m3d>c,那么就

对于d是严格单调递增的,

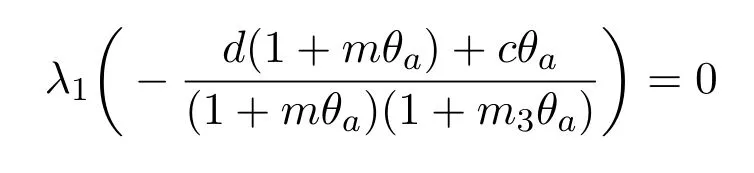
且∃ψ∗≥0满足

下面,给出全局分歧解的存在性条件.

定理3.1假如a>λ1,d>λ1,m3d−c>0,那么问题(6)有分歧点,且在该点邻域内有正解

a∗由

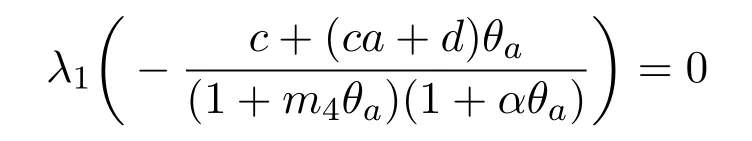
惟一确定,(a(s);Φ1(s),Ψ1(s))是C1连续函数,

且有

证明取

其中

由

得

由于

可化为

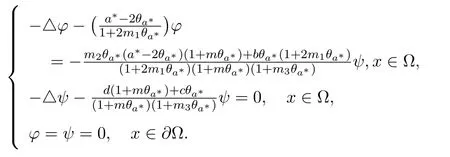
当ψ≡0时,由算子L(a∗)可逆推出φ≡0,反证法得ψ不恒为零,由引理3.2知,

从而

算子L(a∗;0,0)有核空间

且

取L(a∗;0,0) 的自伴算子L∗(a∗;0,0),则

再根据Fredholm选择公理得,

于是

取

下面证明

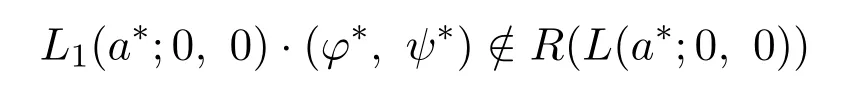
成立.用反证法假设∃(h,k)∈X,满足

可得

从而

上式两边同乘以ψ∗并分部积分得

因为m3d−c>0,θa是严格单点递增函数,故上式左端大于0,与假设矛盾.故∃δ>0和连续曲线

满足

同时有 Φ1(s)Ψ1(s)∈Z满足

最后因为

所以局部分歧正解Γ∗存在.