量子结构和代数结构上的非概率测度

2019-01-12辛小龙

纯粹数学与应用数学 2018年4期

辛小龙

(西北大学数学学院,陕西西安 710127)

1 引言

以概率测度为基础的概率论和统计理论,是现代数学的一门重要分支,在现代科学的各个领域都有重要作用.特别是当今是大数据时代,概率论和统计理论在大数据的挖掘、分析、处理及应用中起着不可替代的作用.然而,随着科学技术和人类社会的快速发展,人们面对的问题越来越复杂,许多问题用概率测度来度量远远不够.比如,概率测度的完备性公理要求

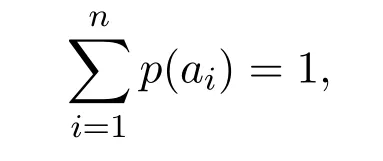
是基于以下假设:任一随机试验中出现的可能结果预先是知道的,并且每次随机试验都有结果发生,而且这些结果都是某些基本事件的组合.然而这一假设在一些问题中是不成立的,例如在量子结构中,两个基本粒子的碰撞试验,可能不产生任何粒子.因而有必要引入更一般化的测度,为复杂问题的研究提供更多的工具.量子结构和代数结构上的态,是近年来发展的一种非概率测度,它在研究基于量子结构和代数结构的模型中,起到了重要作用.本文将对一些量子结构和代数结构上的态和内态方面的研究作一个总结回顾,并给出一些研究工作的展望.

2 量子结构和代数结构上的态

1933年,Kolmogorov出版了关于概率论基础的第一部著作,首次将概率论公理化表示为一门严谨的数学分支[1].按照Kolmogorov的理论,一个概率测度是一个σ-可加的概率测度P,它是定义在一个非空集的子集族上的一个σ-代数S上的.这个模型非常重要,被应用于大学概率论的基本课程中.

然而,在该著作发表不久,人们就意识到Kolmogorov的公理化并不能描述所有的基于量子机制的测度.Heisenberg不确定性原理指出:一个基于粒子的位置x和动量p不能以任意可描述的精度同时被测量.如果用∆mp和∆mx表示用态m对p和x测量的不精确度,则

其中和h是 Planck′s常数.

Birkho ff和Von Neumann证明了:量子机制的(随机)事件适合比Boolean代数更一般的系统,这样的系统被称为量子逻辑或量子结构.目前,已有的各个层次的量子结构,诸如：布尔代数,正交模格和偏序,正交代数,D-偏序集,效应代数.量子结构是代数结构,其中基本运算往往是部分的.

1974年,作为概率侧度的类似,Finetti[3]引入了效应代数上的态,它是一个有限可加映射

它保持所有存在和(a+b),并适合

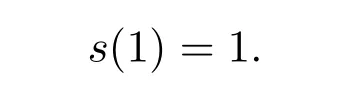
效应代数另一个重要例子是具有强单位元u的Abeian偏序群G.如果限制在区间

我们就可获得一个效应代数,它具有一个群的加法运算,限制在[0,u].这样的效应代数被称为是区间效应代数.一般地,一个效应代数可以没有任何态；但每一个区间效应代数至少承认一个态.充许一个效应代数E变成一个区间效应代数的重要性质是Riesz分解性质(RDP),按照这个性质,单位元的任何两个分解有一个公共加细[4].因此,这样的效应代数E同构于一个具有强单位的Abelian偏序群的一个区间[0,u].

1958年,Chang引入了MV-代数,这是为了建立无限值 Lukasziewicz逻辑的模型而引入的[5].众所周知的 Mundici定理指出,每一个 MV-代数都是某个具有强单位的 Abelianℓ-group的区间,并且在MV-代数簇和具有强单位的Abelianℓ-group范畴之间存在一个范畴等价[6].紧接着,Kpka和Chovanec,证明了以下事实:每一个MV-代数都是效应代数[2].此外,每一个MV-代数是一个格序效应代数并且适合RDP.反之,每一个具有RDP的格序效应代数能被看成是一个MV-代数.

在MV-代数被引入40年后,Mundici在MV-代数上引入了态的概念,它是一个可加函数并保持部分加法.由于态本身不是一个代数运算,具有态的代数系统不构成泛代数.然而,对于量子结构理论态是一个基本概念,特别是在D-偏序集和效应代数的研究中,它有非常重要的作用[2].

如前所述,存在两个概率测度的概念:Kolmogorov的σ-可加的概率测度和 de Fineti的有限可加测度的概念,前者有技术优势,但是后者更直观.Kroupa和 Panti[7-8]证明了在紧的 Hausdor ff拓扑空间上子集构成的一些Borelσ-代数上,通过一个唯一正则(σ-可加)Borel概率测度,MV-代数上的任一个态能被表示成为一个标准积分.这个结果也被一般化到效应代数上(具有RDP)[9].通过研究可以看到,关于态的研究,Kolmogorov和De Fineti方法(关于概率测度)没有实质差别.虽然对量子结构研究的原始驱动是量子机制,但是像不等式(1)所示的现象在许多不同领域都能观察到,诸如计算机科学、精神病学、神经科学、量子智能(quantum brain)[10]、量子心理学(quantum psychology)[11]和量子计算.

存在许多新的代数结构能够在量子结构的框架下来研究,诸如:BL-代数,MTL-代数及其非可换一般化,伪MV-代数,伪效应代数,伪BL-代数.然而,重要的是要在这些代数中引入态的类似概念.对伪MV-代数,这一点是直接可以做到的.因为任何一个伪MV-代数是一个有着强单位的ℓ-群G的一个区间.同此,我们能得到一个部分运算“+”,即群的加法在区间[0,u]上的限制.但在其他结构,诸如BL-代数,伪BL-代数,我们不清楚如何统一定义一个态.因而,在BL-代数和伪BL-代数中存在两个态的概念,Bosbach态和Riean态.

早在 1934年,Marty提出代数超结构的概念[12].尤为突出的是,Corsini和 Leoreann于2003年在其专著中[13],一方面概括了超结构理论,另一方面阐述了超结构在一些领域中的应用,如:几何、超图、格论、自动化、密码、人工智能和概率统计等.需要指出的是,1994年,Vougiouklis在第四届AHA国际会议上引入一类新的超结构―Hv-结构,它实际上将公理体系中等式改为非空交[14].特别地,近十年来,国内外许多专家学者致力于代数的超逻辑结构研究.近年来,我们在超逻辑代数上引入并研究了态,在超MV-代数[15]、超BCK-代数[16]、超EQ-代数等超结构上引入并研究了态的概念,得到了一些新的结果,如:在代数结构上,Bosbach态一定是 Riean态,然而在超结构上,Bosbach态可以不是Riean态.同时,我们应用态研究了相应代数的结构和性质,进一步拓宽了态的研究领域,为用态来研究超逻辑系统奠定了重要基础.

研究表明,态是模糊逻辑中处理不确定性推理的一个有效方法,同时也是研究对应逻辑代数的有力工具,基于此,近年来国内外很多学者致力于逻辑代数上态的存在性的研究,如:Dvurecenskij[17]指出不同于MV-代数,存在一些伪 MV-代数其上不具有态,受此启发,Ciungu[18]研究了伪MTL-代数上的态,证明了存在线性的伪MTL-代数其上不具有态.2008年,刘练珍教授[19]证明了每一个R0-代数都存在Bosbach态;在文献[20-22]中,研究了MTL-代数上的Bosbach态和Riean态,证明了一个MTL-代数存在Bosbach态当且仅当它有奇异滤子,同时在最近发表的关于EQ-代数上的两类特殊(前)滤子[22]的论文中,进一步提出一个公开问题：如何定义EQ-代数上的奇异滤子和态,并讨论二者之间的关系.最近,我们研究了EQ-代数上的态的存在性问题.引入并研究了EQ-代数上的Fantastic滤子,用Fantastic滤子刻画了EQ-代数上态的存在性问题.我们得到了以下结果:一个剩余EQ-代数有Bosbach态当且仅当它有Fantastic滤子;一个好的EQ-代数有一个态射当且仅当它有一个素Fantastic滤子.我们还研究了伪对合EQ-代数的Riean态的存在性.进而,我们研究了半可分EQ-代数上态的存在性问题,证明了每一个半可分剩余EQ-代数都承认一个Riean态.这些工作一般化了剩余格、NM-代数、MTL-代数、BL-代数等结构上的态的存在性研究的现有结果,建立了态的存在性研究领域的一般性框架.

3 代数结构上的内态理论

由于逻辑代数的态不是它自身的算子,因而具有一个态的逻辑代数一般不是一个泛代数,所以它们并不能自然地诱导一种断言逻辑(assertional logic)[23].为了给模糊事件的概率提供代数基础,Flaminio和Montagna[24-25]应用概率方法引入了一种可代数化逻辑,它的等价代数语义恰好是具有内态(internal states)的MV-代数簇,其中内态的性质来源于态的相应性质.此后,很多学者致力于逻辑代数上内态的研究,相继出现了态BL-代数[26]、态Rl-半群[27]、态BCK-代数[23]、态相等代数[28]等具有内态的逻辑代数.Di Nola和Dvurecenskij[29-30]引入了态射 MV-代数,它是一类特殊的态 MV-代数,次直积不可约态射 MV-代数也被刻画.Rachunek与lounov[31]引入并研究了态伪MV-代数.

剩余格是一类基本的逻辑代数,它包含MV-代数、MTL-代数、BL-代数等重要的逻辑代数作为它的子类,同时也是EQ-代数、半Hoop代数的重要模型,因此在剩余格中建立内态理论是一项重要工作.2015年,在文献[32]中,作者在剩余格中引入并研究了内态理论,应用内态刻画了Rl-半群和Heyting代数.进而研究了一个态剩余格L上的全体态滤子SF[L]的结构,得到了SF[L]形成了一个 coherent frame和一个伪补格.2015年,在文献 [33]中,研究了超 BCK-代数上的内态理论.2017年,作者讨论了半Hoop代数上的内态[34].2018年,文献[35]中,作者研究了EQ-代数上的内态理论.这些工作的完成,形成了在内态研究中的独特方法,这些方法对于其余逻辑代数上内态理论的研究有一定的借鉴作用.