抛物线中面积模型的构建与应用

☉江苏省南京市上元中学 徐 芸

抛物线的面积问题是中考数学的重点问题，该类问题一般以抛物线为载体，以图形的面积作为条件或问题进行命题.求解时可以借助特定的面积模型，建立几何面积与抛物线上点的坐标的关系.本文将从教材公式衍生面积模型，然后结合考题具体讲解面积模型的应用方法，以期对师生的备考有所帮助.

一、教材解读，公式探知

三角形的面积计算公式是数学几何常用的公式，但大多数一般三角形难以直接利用公式求解，十分有必要探究任意三角形面积与边长的关系，下面进行详细探究.

探究：图1所示为任意的△ABC，如何表示其面积？又可以怎样理解？

分析：△ABC为任意三角形，根据三角形的面积等于底乘高的二分之一，过点A

图1

二、延伸拓展，模型构建

求解一般三角形面积的问题形式很多，其中以直角坐标系为背景的面积求值题是较为特殊的一类，对于该类题的模型构建，我们同样可以借助上述对面积计算公式的割补方式.

问题：图2所示为直角坐标系中一任意三角形ADE，已知三个顶点的坐标，试求△ADE的面积.

模型：对于△ADE的面积模型的构建有以下两种方式：

方式1：过点A作x轴的平行线AF，交DE于点F，再作EH⊥AF于点H，DG⊥AF于点G，则EH+DG=yD-yE.

参考上述分割方式，△ADE可分割为有共同底AF的△ADF和△AEF，两个三角形具有共同底AF，则S△ADE=AF·（DG+EH）=

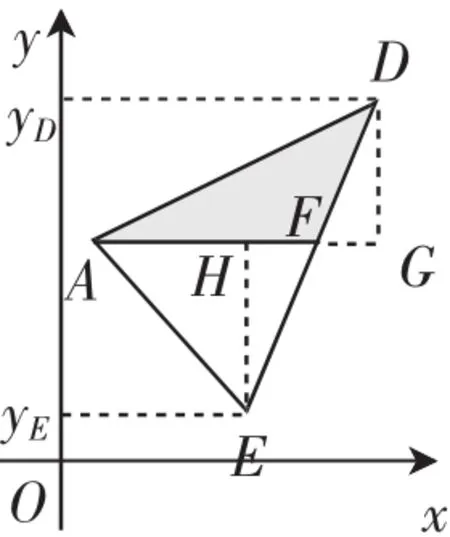
图2

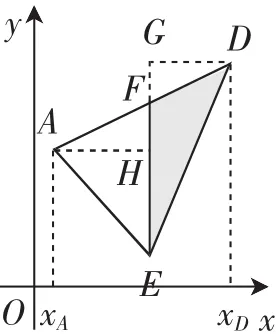
图3

方式2：如图3，过点E作y轴的平行线EF，交AD于点F，再作AH⊥EF于点H，DG⊥EF于点G，则AH+DG=xD-xA.

病原菌可以在病残体上越冬，也可以附着在种子表面在土壤中越冬，成为次年初侵染来源，一旦环境条件适宜病原菌便形成分生孢子。白菜白斑病的分生孢子具有黏着性干燥的气候条件并不适宜分生孢子的传播，适当的降雨非常有助于分生孢子的传播扩散，这也是秋季高湿的气候条件下白菜白斑病发病严重的主要原因。分生孢子还可以借助风力传播，通过植物的气孔等自然空口进入到植株内部，环境条件适宜的情况下引起植物病害并形成新的分生孢子继续多次侵染。

上面分别通过作x轴和y轴的平行线对一般三角形ADE进行了分割，然后利用共底线段的长和关键点的坐标完成了面积模型的构建，其中最为显著的区别在于点的坐标的利用，这是由对应的条件所决定的，也是后续利用模型解题时需要处理的关键点.

三、应用模型，例题探析

在历年的中考函数压轴题中，都有涉及曲线上三角形面积求值的题.对于该类问题，可以通过图形分割的方式，采用上述两种方式构建面积模型，从而将问题转化为求解关键点的坐标，下面将结合考题分别探析.

例1（2018年黄冈市中考卷第22题）已知直线l：y=kx+1与抛物线y=x2-4x.

（1）求证：直线l与该抛物线总有两个交点；

（2）设直线l与该抛物线的两个交点为A、B，O为原点，当k=-2时，求△OAB的面积.

解析：第一问求证交点的个数只需要联立直线与抛物线的方程，根据判别式的正负判断证明.下面主要分析第二问利用上述构建的模型求三角形面积的具体过程.

当k=-2时，可得直线l的表达式为y=-2x+1.联立y=-2x+1与抛物线y=x2-4x，可求得点A和B的坐标，分别为A（1-，2-1）、B（1+，-1-2）.采用上述面积模型构建的方式1，以x轴为图形分割线，对△OAB进行面积割补，设AB与x轴的交点为C，则S△AOB=S△AOC+S△BOC.

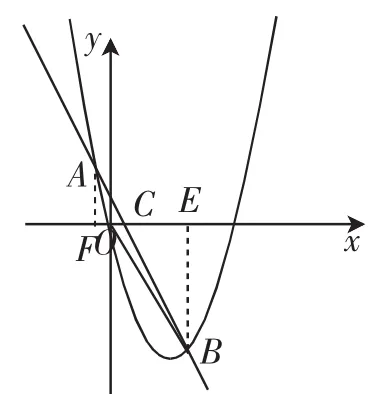
图4

如图4，过点A作x轴的垂线，垂足为点F，过点B作x轴的垂线，垂足为点E，则BE，所以·（AF+BE）.而AF+BE等于点A和点B纵坐标的差值，即AF+BE=|yA-yB|，从而完成了△OAB的面积模型的构建只需要将具体点的坐标代入即可.

例2（2018年江苏省盐城市中考卷第27题）如图5①所示，在平面直角坐标系xOy中，抛物线y=ax2+bx+3经过A（-1，0）、B（3，0）两点，且与y轴交于点C.

（1）试求抛物线的表达式.

图5

（2）如图5②所示，用宽为4个单位长度的直尺垂直于x轴，沿着x轴进行左右平移，直尺的左右两边所在的直线与抛物线相交于点P、Q（点P位于点Q的左侧），连接PQ，在线段PQ上方有一动点D，连接DP、DQ.

（II）在直尺平移过程中，△DPQ的面积是否会取得最大值？如果会，请求出面积的最大值；如果不会，请说明理由.

解析：第一问利用待定系数法即可求得抛物线的表达式，下面主要分析第二问的面积模型求解.

对于第（I）问，虽然是求△DPQ面积最大时点D的坐标，但考虑到可以利用点D的坐标来构建△DPQ的面积模型，则依然可以利用上述模型构建方式.考虑到求点D的坐标可以采用方式2，过点D作y轴的平行线，交PQ于点E，如图6所示，DE将△DPQ分割为△DEP和△DEQ，且两个三角形可以视为拥有共同底PE，则S△PDQ=S△DEP+S△DEQ，根据模型可进一步表示为DE·|x-x|.则只需QP要设出点D的坐标进行参数表示即可.由于尺宽为4，则点P和点Q的横坐标有如下关系：xQ-xP=4，则只需要表示出DE的长即可.可设点D的坐标为（m，-m2+2m+3），则点，所以DE=yD-yE=-m2+3m+.代入上式，可得，可得面积最大时，进而可得点D的坐标为

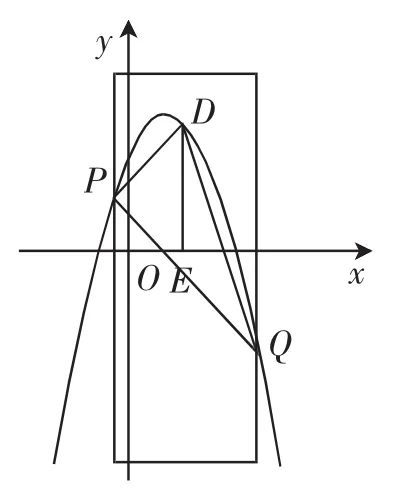
图6

对于第（Ⅱ）问，同样采用上一问的面积模型.S△DPQ=点P、D的坐标不确定，可分别将其设出.设点P（m，-m2+2m+3），则点Q（m+4，-m2-6m-5）.设点D（t，-t2+2t+3），则点E（t，m2+4m+3-2mt-2t），进而可得DE=-t2+2t+3-m2-4m-3+2mt+2t.代入面积模型，可得S△DPQ=-2（t-m-2）2+8≤8，显然t=m+2时，S△DPQ有最大值8.

评析：上述两道考题均为抛物线问题，求解过程分别采用了引文中的面积模型，从本质上讲依然是对三角形面积计算公式的变形使用，所不同的是，在选取模型构建方式时存在差异，这是由于题干条件的不同造成的.如例2需要求解点D的坐标，则选取分割方式时必然要结合点D，这也是面积模型的另类解题应用.另外，在利用面积模型求解以曲线为背景的几何面积问题时可以遵循以下策略：首先确定分割方式，然后建立一般图形的割补模型，最后基于点的坐标参数建立完整的面积模型.实际应用时需灵活变通，因题而变，巧用模型.

四、解题思考，教学建议

1.传达模型意识，掌握解题策略

从上述考题的求解可以看出，利用数学模型分析问题往往可以获得良好的解题效果，模型是构建解题思路的重要工具，以其为出发点开展问题探究，不仅可以简化思路，而且模型是对问题本质的解释，在应用过程中可以帮助理解问题内涵，形成问题求解的基本策略.“授人以鱼不如授人以渔”，在平时的教学中，教师要向学生传达模型意识，以掌握问题的解法为考题研究的出发点.如教学面积模型时，首先需要基于面积计算公式，通过适当的变形构建面积问题的解题模型，然后结合实际问题引导学生掌握利用模型求解的具体方法，形成完善的解题思路.这样由“数学公式、定理”出发，构建“数学解题模型”，最后“结合模型解题”的教学模式更有利于学生理解模型本质，形成深刻的策略认识.

2.渗透模型思想，提升核心素养

上述利用面积模型求解相关问题，其背后所隐含的是模型思想的应用体现.思想方法作为解决问题的指导思想和解题策略，虽然在具体解题中没有明确指明，但是最能体现学生学科素养的灵魂所在.从思想方法层面强化学生的解题能力，不但可以显著提高解题效率，更能提升学生的解题思维，而后者才是中学教学的意义所在.例如，上述讲解的面积模型背后的模型思想，通过图形割补的方式对面积进行转化，从而构建出利用点的坐标求解图形面积的思路，这个过程中涉及图形分割、面积转化、坐标分析等内容，是数学定理完美融于基本图形的体现.在实际教学中，十分有必要进行模型思想的渗透，让学生经历模型构建的过程，充分感受思想方法指导解题的便利性，从中积累经验，在潜移默化中获得思想的提升.

五、写在最后

对现今中考问题的研究可知，每道优秀的考题都不是简单的知识点拼合，其背后必然隐含着特定的数学思想，有着一定的解题模型，遵循正确的构建策略必然可以巧妙突破考题.因此深入挖掘考题，透析结构与模型应作为考题学习的重点.虽然不同地区的考题风格存在差异，但解题模型均来自于数学教材，以教材定理、公式作为模型研究的出发点，才能真正理解模型，理解考题，提升解题能力.