超声吸收体边界条件的分析

沈国峰，余瑛，张鹤林，程春雷，汪灿华



超声吸收体边界条件的分析

沈国峰1*，余瑛2*，张鹤林2，程春雷2，汪灿华2

(1. 上海交通大学生物医学工程学院，上海 200240；2.江西中医药大学计算机学院，江西南昌 330004)

超声吸收体的边界条件分析对于求解超声吸收体表面温升与入射波声强的函数关系至关重要。通过分析在超声吸收体与水和与空气界面处超声辐照的物理过程，分别得到超声吸收体与水界面处的平均传热系数与焦点声强之间的函数关系式和超声吸收体与空气界面处的复合传热表面系数与温差的函数关系式。通过仿真分析了不同条件下两个界面处的传热系数对超声吸收体与空气界面温升的影响。实验结果表明，当辐照时间较短时，对于超声吸收体与空气界面的温度变化，超声吸收体与水界面可以认为是一个无限远且温度恒定的边界，超声吸收体与空气界面可以认为是一个符合第一类边界条件的连续热传导。

高强度聚焦超声；声场测量；红外热成像；超声吸收体；边界条件

0 引言

高强度聚焦超声(High Intensity Focused Ultrasound, HIFU)三维声场分布是衡量HIFU治疗探头设计与制造工艺、HIFU治疗效果好坏的关键因素，也是衡量设备安全性与效率的重要指标[1-3]。此外，HIFU三维声场分布也对治疗计划的制定有着重要的参考意义[2]。

近年来，基于红外热成像技术的聚焦超声声场参数快速定量测量方法，得到了日益广泛的关注[1-9]。该项技术的主要原理是利用实时的扫描热成像技术对被测物表面进行温度测量，根据被测物的声热参数推算出引起被测物表面温度场变化的入射波声强分布和大小，再将测量物在HIFU声场中不断地上下平移，就可以快速得到HIFU声场三维分布[3,10-11]。为了准确地推算出入射波声强的大小，需要合理准确地建立其超声吸收体表面温升模型，其中超声吸收体边界条件的确定尤为重要[12]。

本文通过分析超声吸收体/水和空气界面处在超声辐照过程中的物理过程，分别得到相关的传热系数函数关系式，并仿真分析了超声辐照对超声吸收体/空气界面的温升影响。

1 超声吸收体/水界面

超声吸收体/水界面在超声辐照时，界面附近的水流由于受到超声波的作用产生声流(Acoustic Stream)，并对界面处产生冲击作用，形成冲击传热[13]，呈现一个圆柱状的分布[14]，故而可以将此冲击传热类比为单个圆嘴喷射流。超声吸收体/水界面处的平均传热系数可以通过求解焦域内的平均流速来推导获得。

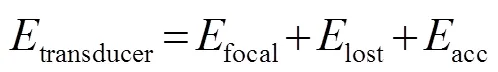
根据质量守恒定律，焦域内流体(水)位移的体积变化与换能器表面产生的体积变换相等，所以焦域内的能量可以表示为[14-15]

由于在焦域内，换能器产生的能量主要集中在此，并且呈现一个沿声束轴对称的圆柱状，所以本文将焦域内由于超声辐照引起的流体流动类比为单个圆喷嘴射流的流场结构。建立以滞止点为圆心、半径为的圆，被冲击的超声吸收体表面的平均换热系数可以表示为[14-17]

本文结合PLL合成频率源的相位噪声模型，计算分析了各噪声源的相位传递函数特性，并对汽车防撞雷达频率源的相位噪声进行估算与仿真，测试结果为-87.1 dBc/Hz@1 kHz，满足要求。与其他文献相比，本文基于相位噪声分析设计的频率源具备低相位噪声的显著优势，这也为汽车防撞雷达频率源的研制提供了一种可借鉴的设计思路。

2 超声吸收体/空气界面

受红外线穿透能力的限制，需要在红外摄像仪和超声吸收体之间引入空气界面。当超声吸收体受到辐照时，其超声吸收体/空气表面可能会产生对流传热和辐射传热，对于换热面积为的超声吸收体来说，其表面的复合传热的总换热量可以表示为[16]

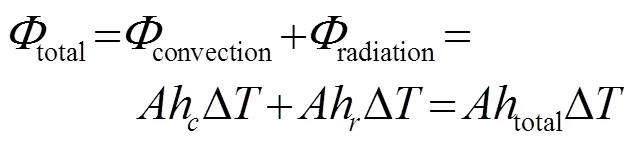
综合式(10)～(12)可以得到复合传热表面的传热系数为

3 仿真与讨论

分别改变超声吸收体两个界面处的传热系数，通过仿真研究其对超声吸收体/空气界面处温升的影响。仿真中使用的热学参数如表1所示，其中为入射波的角频率，，超声辐照时间设定为200 ms。超声吸收体内部热源按照如下公式进行计算[14-15]：

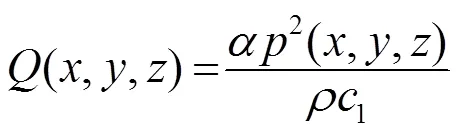
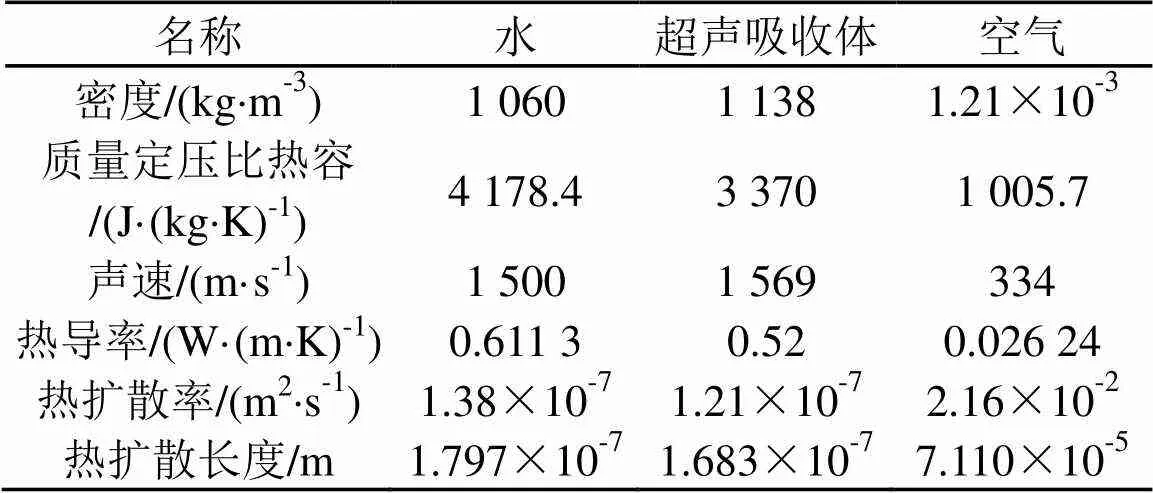
表1 仿真中各类媒质的热学参数

表2 不同声吸收体/水界面处平均换热系数引起的超声吸收体/空气表面最大温升

在超声吸收体/空气界面处存在对流传热和辐射传热时，从式(13)可以看出，超声吸收体/空气界面复合传热表面的传热系数是一个关于超声吸收体表面温度与周围温度差的函数。当温差为20 °C时，，当温度差为100 °C时，，其中辐射传热表面的传热系数所占的比例从0.08%增加到0.96%，所以在计算复合传热表面传热系数时可以忽略辐射传热。

表3展示了超声吸收体/空气界面处使用热对流传热模式和热传导模式计算的表面最大温升的差异。其仿真条件为：超声吸收体/水界面处的传热系数为，超声吸收体厚度为2 mm，加热时间为200 ms，入射波轴线最大声强分别为1 000、2 500、和3 500 W.cm-2时对应的分别为8、10、20。可以看出，当表面温差小于100 °C时，使用热对流传热和辐射传热复合而成的表面传热系数与使用热传导条件下计算的结果十分接近，最大温升的差异小于0.7%。其原因可能是由于超声吸收体/空气界面处的温升虽然在较短时间内有一个显著的提升，但是空气热传导也需要一个弛豫时间。由温升决定的瑞利数()并没有超过一定的限定值，未能使得界面处形成对流传热，在超声吸收体/空气界面处，可以认为热传导起主要的作用。

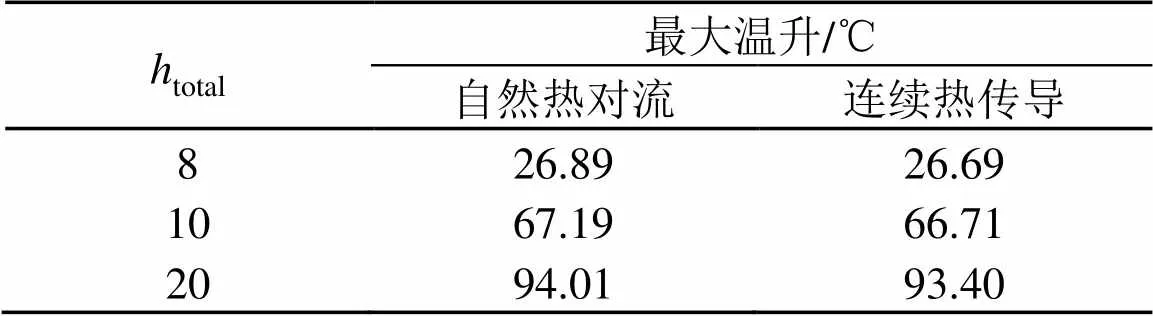
表3 热对流传热模式和热传导模式计算的超声吸收体/空气表面最大温升

4 结论

通过红外热成像技术测量聚焦超声声场分布时，超声吸收体的两个界面处的热力学边界条件的确定，对于求解入射波声场强度具有重要的意义。

本文使用集中参数法分析了焦域内的能量分布，将声流引起的冲击传热类比为单个圆嘴喷射流，通过求解出焦域内的平均流速得到超声吸收体/水界面处的平均传热系数与焦点声强之间的函数关系式，如式(9)所示。通过仿真，可以得到当超声辐照时间较短时，超声吸收体/水界面处的强冲击传热对超声吸收体/空气界面处的温升无明显影响，因此在实际求解中可以将此界面设定为一个无限远且温度恒定的边界条件。

本文通过分析超声吸收体/空气界面处的各种传热，得到复合传热表面系数total。仿真结果表明，在此界面处辐射传热可以忽略不计，并且在超声辐照时间较短时，超声吸收体/空气界面处可以认为是满足界面连续条件的热传导。

[1] MILORO P, CIVALE J, RIVENS I, et al. The feasibility of thermal imaging as a future portal imaging device for therapeutic ultrasound[J]. Ultrasound in Medicine & Biology, 2016, 42(8): 2033-2038.

[2] HAAR G T, RIVENS I, CIVALE J, et al. Quality assurance and field characterisation for MRgHIFU treatments: their need and the challenges presented[J]. Journal of Therapeutic Ultrasound, 2015, 3(Suppl 1), O66-O66.

[3] YU Y, SHEN G, ZHOU Y, et al. Quantitative assessment of acoustic intensity in the focused ultrasound field using hydrophone and infrared imaging[J]. Ultrasound in medicine & biology, 2013, 39(11): 2021-2033.

[4] KHOKHLOVA V A, SHMELEVA S M, GAVRILOV L R, et al. Infrared mapping of ultrasound fields generated by medical transducers: Feasibility of determining absolute intensity levels[J]. J. Acoust. Soc. Am., 2013, 134(2): 1586-1597.

[5] GIRIDHAR D, ROBINSON R A, LIU Y, et al. Quantitative estimation of ultrasound beam intensities using infrared thermography-Experimental validation[J]. J. Acoust. Soc. Am., 2012, 131(6): 4283-4291.

[6] SHAW A, KHOKHLOVA V, BOBKOVA S, et al. Calibration of HIFU intensity fields measured using an infra-red camera[J]. Journal of Physics: Conference Series, 2011, 012019.

[7] MYERS M R, GIRIDHAR D. Theoretical framework for quantitatively estimating ultrasound beam intensities using infrared thermography[J]. J. Acoust. Soc. Am., 2011, 129(6): 4073-4083.

[8] SHAW A, NUNN J. The feasibility of an infrared system for real-time visualization and mapping of ultrasound fields[J]. Physics in Medicine and Biology, 2010, 55(11): N321.

[9] SHAW A, HODNETT M. Calibration and measurement issues for therapeutic ultrasound[J]. Ultrasonics, 2008, 48(4): 234-252.

[10] YU Y, SHEN G, BAI J, et al. The ultrasound fields estimation using uncooled infrared system[M]. New York, NY, 2012: 469-474.

[11] YU Y, SHEN G, BAI J, et al. A method of estimating ultrasound fields at full power using infrared and hydrophone system[C]//International Conference on Biomedical Engineering & Informatics, Shanghai, 2011, 1456-1458.

[12] HALLER J, JENDERKA K V, SEIFERT F, et al. A comparison of three different types of temperature measurement in HITU fields[J]. Metrologia, 2012, 49(5): 279-281.

[13] 沈阳, 寿文德, 耿晓鸣, 等. HIFU温度场可视化测量初探[J]. 应用声学, 2005, 24(1): 24-27.

SHEN Yang, SHOU Wende, GENG Xiaoming, et al. Visualized measurement of HIFU temperature filed[J]. Applied Acoustics, 2005, 24(1): 24-27.

[14] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 第2版. 南京: 南京大学出版社, 2001.

DU Gonghuan, ZHU Zhemin, GONG Xiufen. Fundamentals of acoustics[M]. Second Edition, Nanjing: Nanjing University Press, 2001.

[15] 万明习. 生物医学超声学[M]. 北京: 科学出版社, 2010.

WAN Minxi. Biomedical ultrasonics[M]. Beijing: Science Press, 2010.

[16] 陶文拴. 数值传热学[M]. 西安: 西安交通大学出版社, 2001.

TAO Wenquan. Numerical heat transfer[M]. Xi’an: Xi’an Jiaotong University Press, 2001.

[17] HOLMAN J. Heat transfer[M]. New York: McGraw-Hill, 1997.

The analysis of absorber’s boundary condition

SHEN Guo-feng1, YU Ying2, ZHANG He-lin2, CHENG Chun-lei2, WANG Can-hua2

(1. School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;2. School of Computer Science, Jiangxi University of Traditional Chinese Medicine, Nanchang 330004, Jiangxi China)

The analysis of boundary condition of acoustic absorber is important for solving the functional relationship between the surface temperature and incident sound intensity. In this paper, the functional relationships between average heat transfer coefficient and focus intensity at the absorber-water interface as well as between composite surface heat transfer coefficient and temperature elevation at the absorber-air interface are established by the analysis of irradiation process. The surface temperature elevation at the absorber-air interface, which is affected by heat transfer coefficients at the two interfaces, is analyzed by simulation. The results show that the absorber-water interface can be regarded as an infinite far and constant temperature boundary and the absorber-air interface can be considered as a continuous heat conduction in accordance with the first class boundary condition when the irradiation time is short.

high intensity focused ultrasound; sound field measurement; infrared imaging; acoustic absorber; boundary condition

TB556

A

1000-3630(2018)-04-0549-04

10.16300/j.cnki.1000-3630.2018.06.007

2017-10-13;

2018-01-04

国家自然科学基金面上项目(11774231)、国家自然科学基金重大科研仪器研制项目(81727806)、国家科技部2017重点研发计划项目(2017YFC 0108900)

沈国峰(1973－), 男, 河北秦皇岛人, 博士,特别研究员, 博士生导师, 研究方向为超声物理治疗技术；余瑛(1979－)，男, 江西南昌人, 博士, 讲师, 研究方向为聚焦超声测量。

*并列第一作者和通讯作者

沈国峰, E-mail: shenguofeng@sjtu.edu.cn; 余瑛, E-mail: 59920079@qq.com