基于时域波束信号高阶谱的目标检测技术

李兰瑞，章新华，刘洪贺，李鹏，刘心语



基于时域波束信号高阶谱的目标检测技术

李兰瑞1，章新华1，刘洪贺2，李鹏3，刘心语4

(1. 海军大连舰艇学院水武防化系，辽宁大连 116018；2. 海军大连地区装备修理监修室，辽宁大连 116041； 3. 哈尔滨工程大学水声工程学院，黑龙江哈尔滨 150000；4. 海军大连舰艇学院政训部，辽宁大连 116018)

为解决常规时域波束形成技术抗噪声能力弱、对弱目标检测能力差的问题，利用高斯噪声的高阶累积量(三阶及三阶以上)为零、非高斯信号的高阶累积量不为零这一性质，对常规时域波束形成后输出的波束信号进行后置处理。首先，对常规时域波束形成后输出的各预成波束信号，分别求其四阶累积量切片谱值；然后，再对各四阶累积量切片谱值分别进行能量累加，得到空间谱图；最后，通过对空间谱在时间上的累积，得到方位历程图。用仿真和海试数据对算法进行了验证：在低信噪比情况下，常规算法不能有效检测到弱目标时，经后置处理后可以有效检测到弱目标。结果表明，与常规时域波束形成算法相比，波束形成后再进行切片谱后置处理的算法增强了对噪声的抑制能力，提高了对弱目标的检测能力。

时域波束形成；四阶累积量切片；目标检测；高阶谱

0 引言

时域波束形成技术是用于声呐听音波束处理的重要方法，然而，常规的时域波束形成技术主要抑制感兴趣方位外的空间噪声，对波束内的背景噪声抑制能力弱。常规时域波束形成技术输出的各预成波束信号中依然存在较强的背景噪声，限制了时域波束形成技术对弱目标的检测能力。水声信号的背景噪声在过往船只较少、相对空旷的海域可以认为是服从高斯分布的，而舰船、潜艇、鱼雷等目标的辐射噪声是非高斯分布的。高阶累积量由于具备了抑制高斯噪声的特点(高斯噪声的高阶累积量(三阶及三阶以上)为零，非高斯信号的高阶累积量非零[1])，已被广泛地应用在阵列信号处理上。现有文献资料显示：Dogan等[2]、Li X K等[3]将高阶累积量应用于阵元域构造虚拟阵元，提高虚拟阵列孔径；高杨等[4]、伍岳等[5]将高阶累积量应用于自适应波束形成，均取得较好的效果。

本文的工作不再将高阶累积量应用于波束形成技术，而是应用于波束形成输出后，对各扫描方位(预成波束)的时域波束形成输出信号分别进行四阶累积量处理，得到每个扫描方位的四阶累积量切片谱，从而得到新的空间谱，以达到在某方位预成波束内含低信噪比目标信号的情形下，抑制高斯背景噪声、提高弱目标检测能力的目的。

1 水声信号的高阶累积量模型

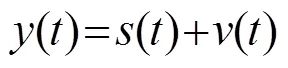
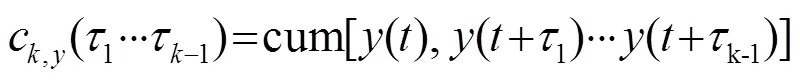
由高阶累积量的独立可加性质可得[8]：

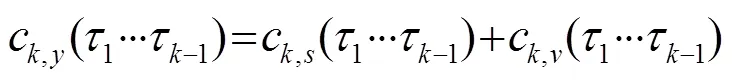
由于高斯信号的高阶累积量(三阶及三阶以上)为零，上式可简化为

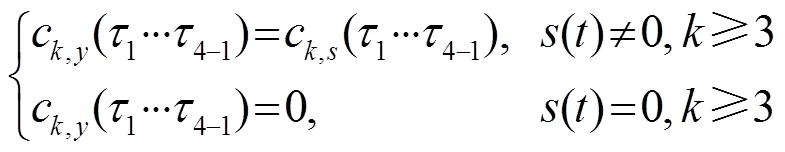
舰船辐射噪声存在二次频率耦合、三次频率耦合和呈对称分布的噪声等情况[9-10]。在高阶累积量算法中，四阶累积量切片谱法在抑制高斯噪声的同时可有效计算出二次、三次耦合频率，且计算速度较四阶累积量更快。

2 基于时域波束信号高阶谱的目标检测方法

根据以上分析，本文采用四阶累积量切片谱，对各预成波束的时域输出信号进行后置处理，用于抑制高斯加性背景噪声，进一步提高弱目标的检测信噪比，工作流程如图1所示。

具体计算过程如下：

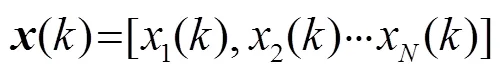
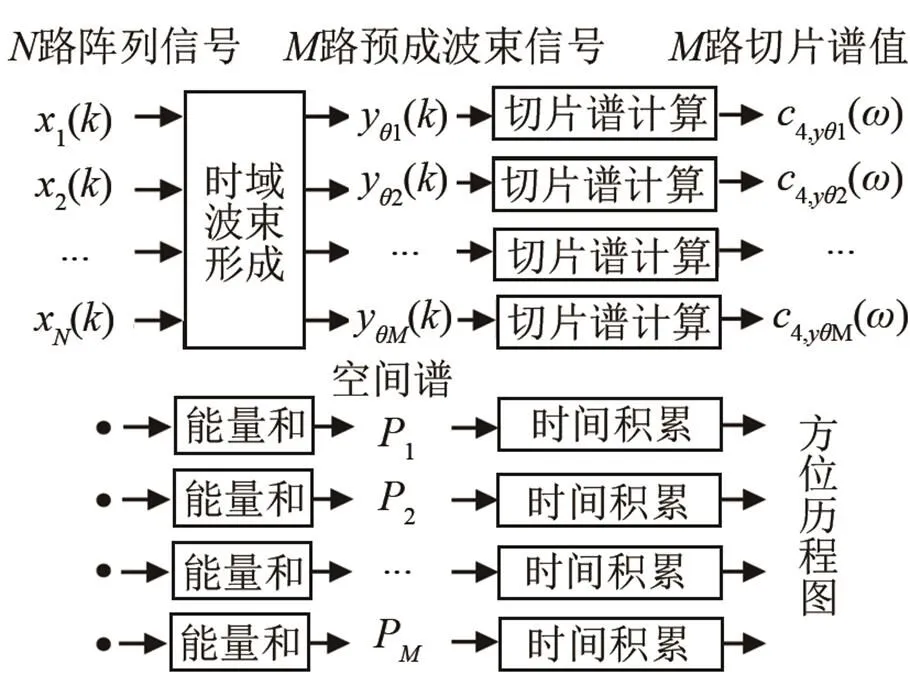
图1 切片谱法工作流程图

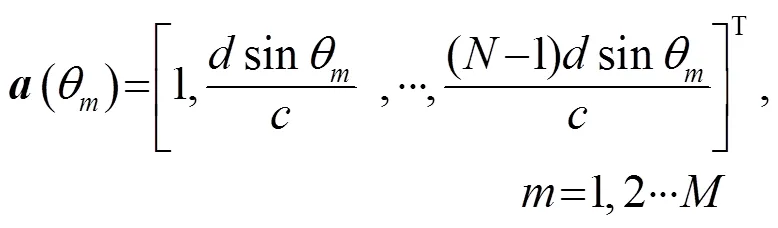
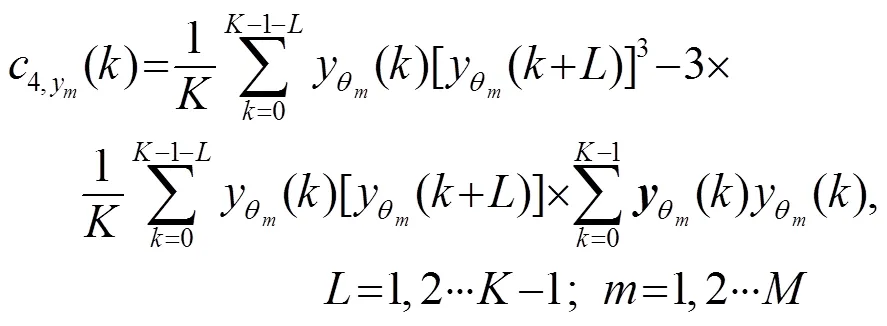
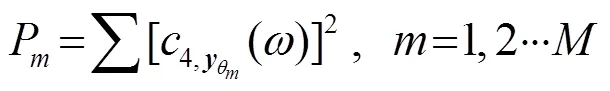
(4) 对空间谱在时间上累积得到时间方位历程图。

3 仿真验证

为验证本文提出的切片谱后置处理算法对弱目标的检测能力，设计了目标信号在不同信噪比下的仿真实验。

阵列仿真参数如下：阵形为均匀线阵，阵元数目为48个，阵元间隔为1 m，采样频率为3 000 Hz；声源信息如下：目标1：入射方向为60°，频率为200 Hz、300 Hz；目标2：入射方向为90°，频率为260 Hz、380 Hz。噪声均为高斯白噪声。

仿真实验一：声源信号目标1的信噪比为-14 dB，目标2的信噪比为-10 dB。

因本文重在研究常规时域波束形成方法和切片谱后置处理方法对弱目标的检测能力，所以，以下重点分析两种方法对目标1的检测情况。从图2中可以发现：在目标1的信噪比为-14dB时，常规时域波束形成和切片谱后置处理算法均可检测到目标1。对目标1，常规时域波束形成后信噪比提高约3 dB，切片谱后置处理之后的信噪比提高约11 dB，切片谱后置处理之后相对处理前信噪比提高约8 dB，因仿真条件比较理想，信噪比提高幅度较高。

取目标1所在方位，即60°方向的时域波束信号，计算并对比其频谱图和切片谱图。如图3所示，四阶累积量切片谱相对于频谱背景噪声更低，线谱特征更加显著。

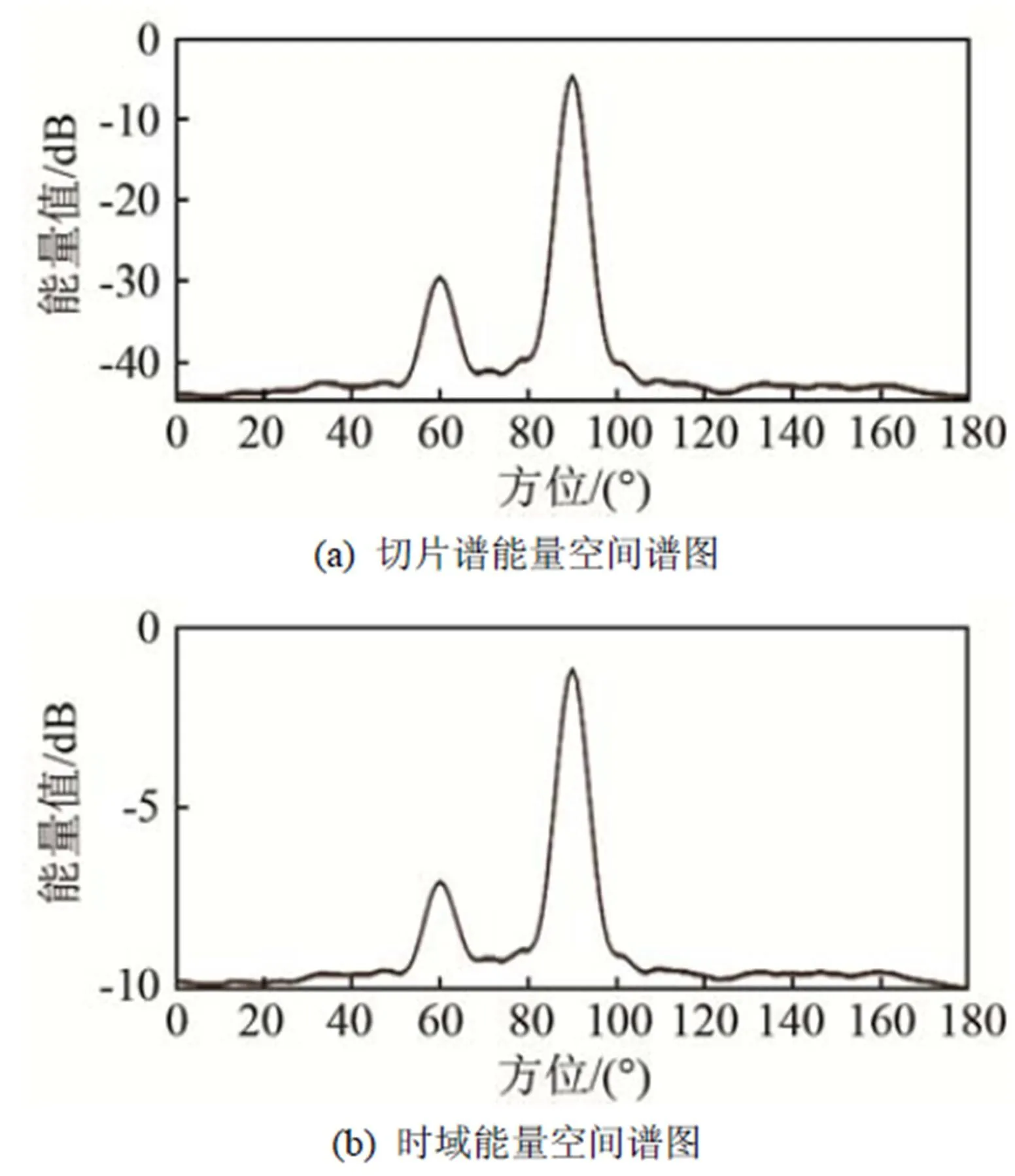
图2 仿真实验一的空间谱图

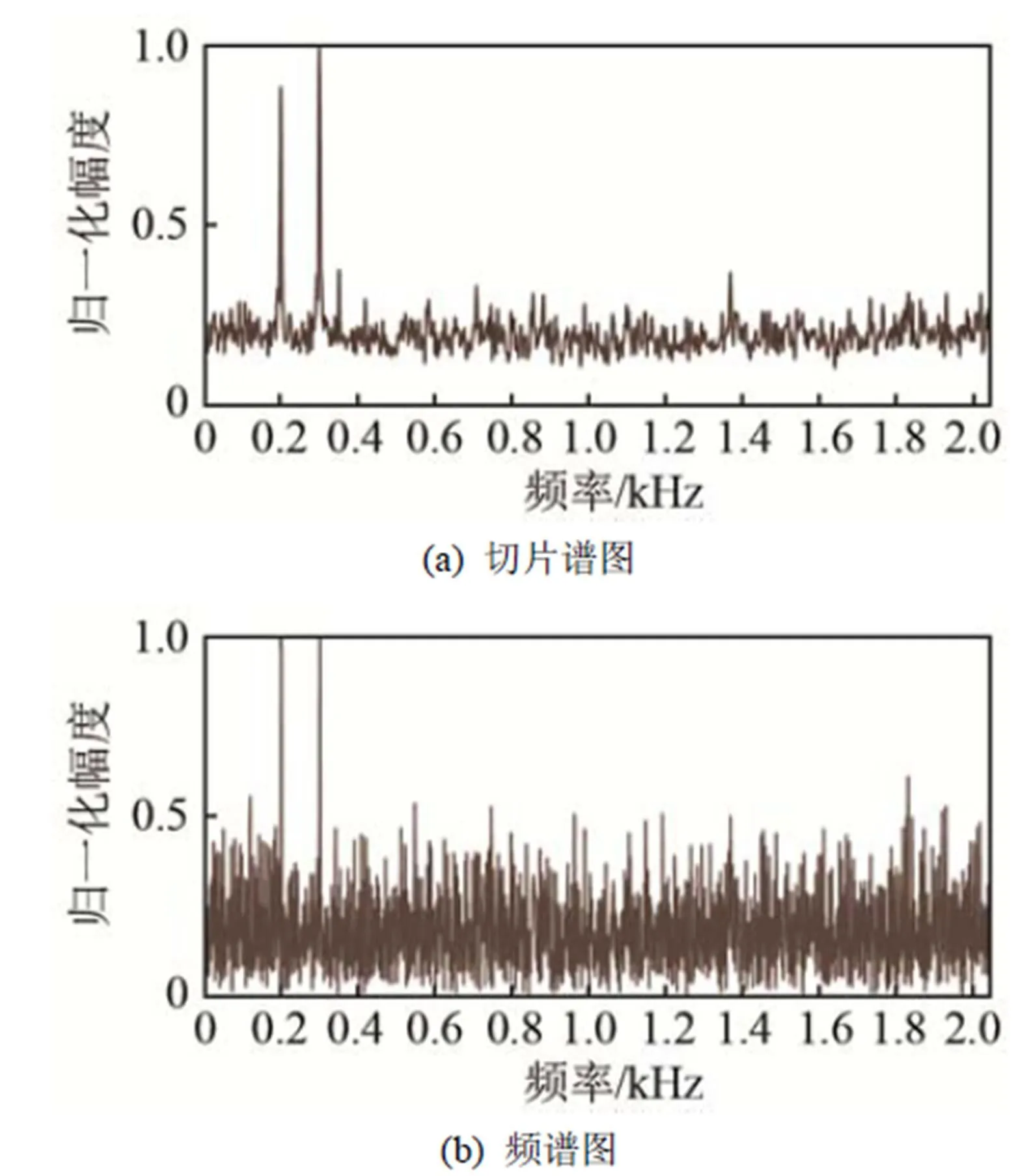
图3 目标1的切片谱、频谱对比图(SNR= -14 dB)

仿真实验二：声源信号目标1的信噪比为-18 dB，目标2的信噪比保持为-10 dB不变。

从图4中可以发现：当目标1信噪比为-18 dB时，常规时域波束形成后对目标1信噪比提高不足1 dB，未有效检测到目标1；切片谱后置处理之后对目标1信噪比提高约7 dB，有效检测目标1。分析目标1所在方位，即60°方向的时域波束信号，如图5所示：在频谱图中，200 Hz频率点已经淹没在背景噪声中，四阶累积量切片谱可以有效地检测到200 Hz处的线谱。

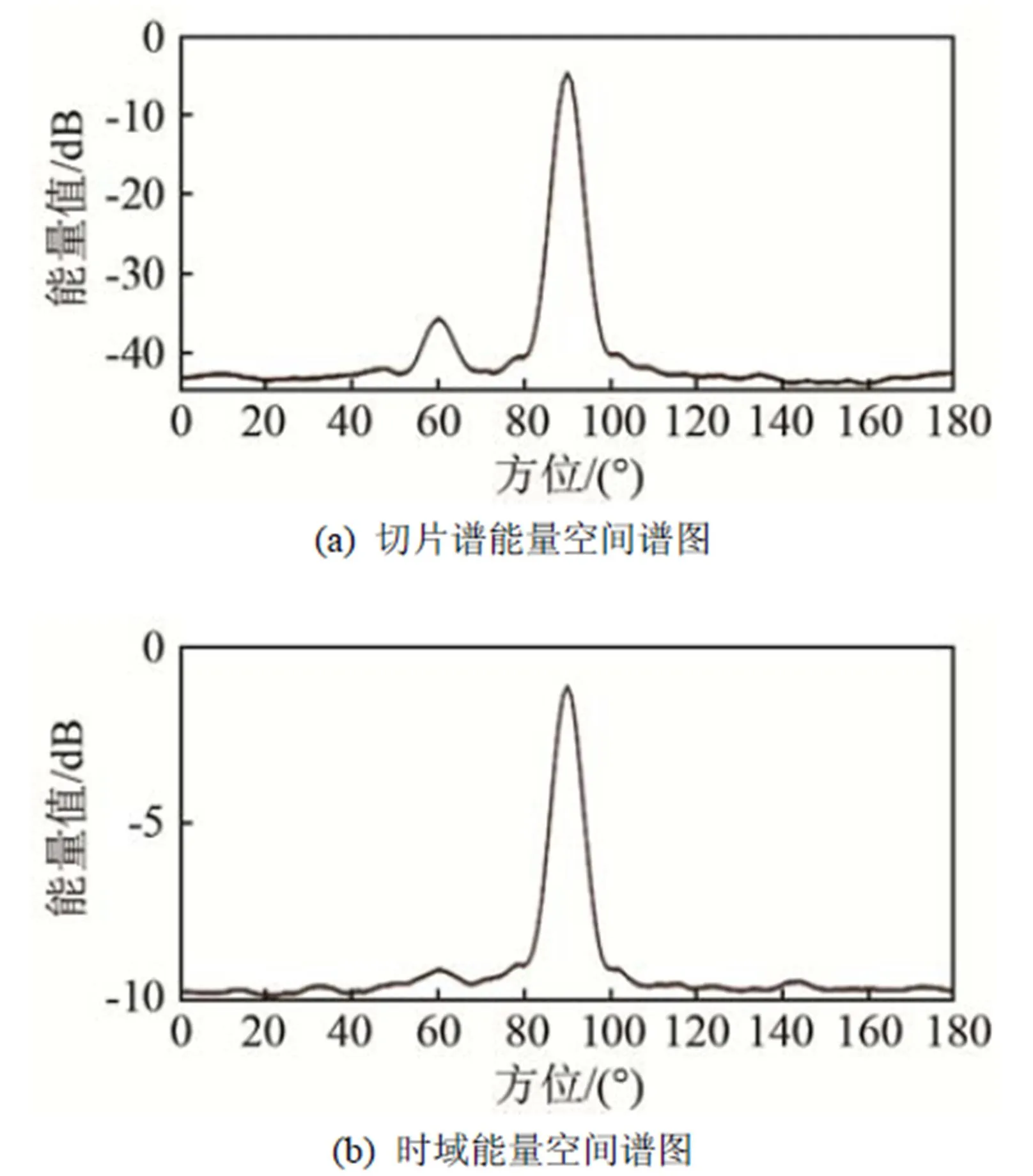
图4 仿真实验二的空间谱图

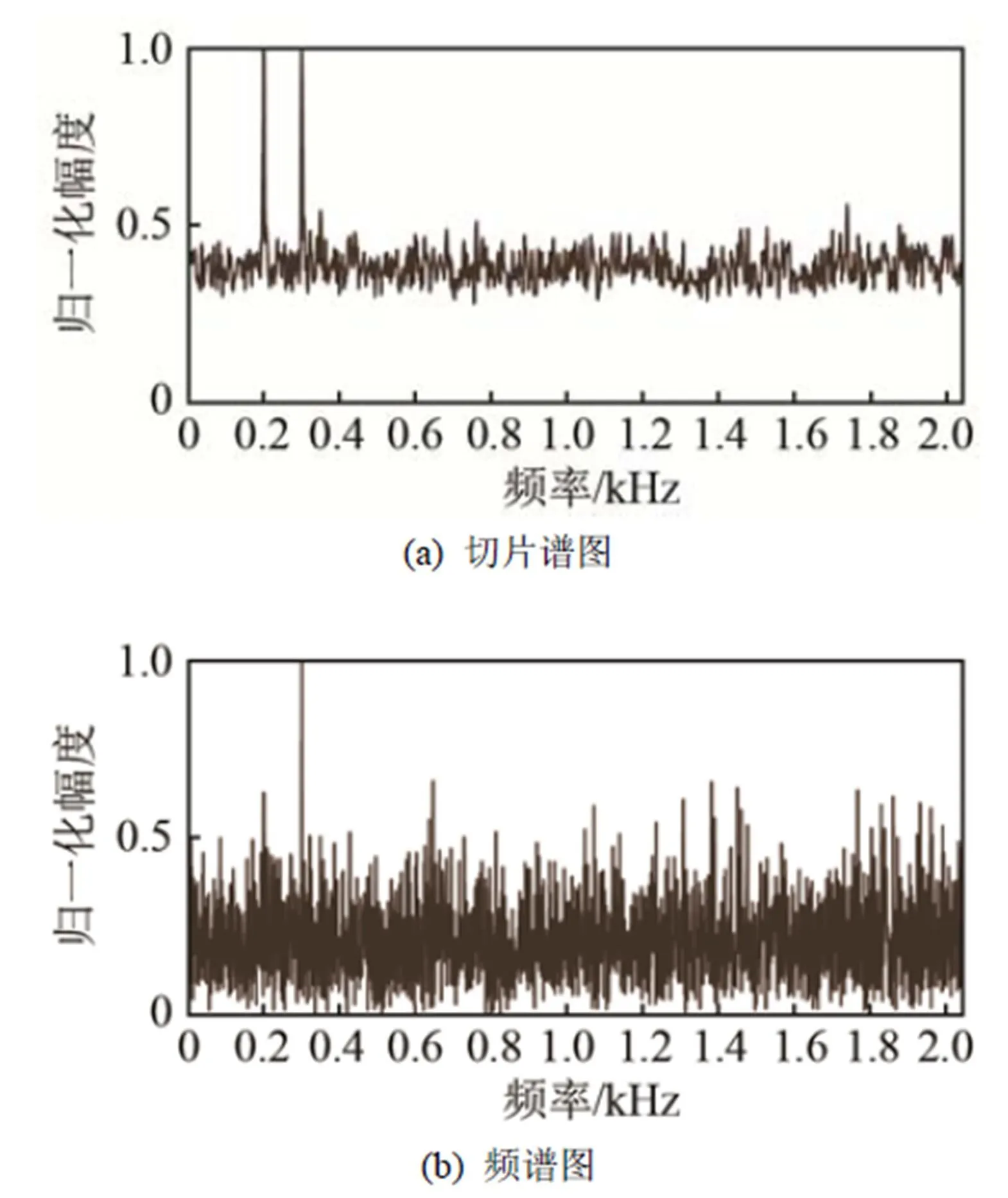
图5 目标1的切片谱、频谱对比图(SNR= -18 dB)

以上仿真实验结果证明，通过对预成波束的时域输出信号进行切片谱后置处理，有效抑制了背景噪声，提高了算法对弱目标的检测信噪比。

4 海试数据验证

下面采用某型听音声呐的海试数据对算法做进一步的检验。取10 s海试数据，分别计算常规时域波束形成后的方位历程图和切片谱后置处理后得到的方位历程图，如图6、图7所示。

图6 常规时域波束形成方位历程图

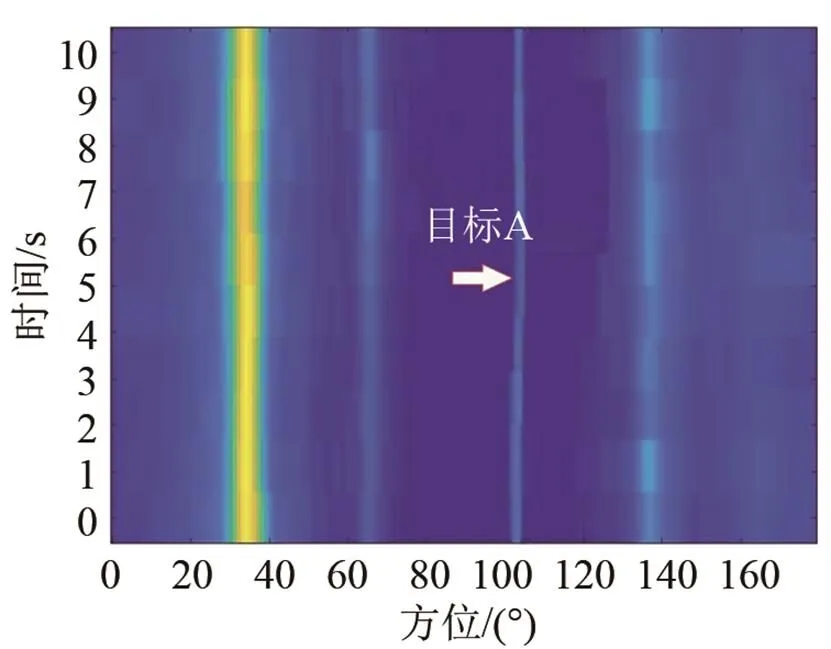
图7 切片谱法方位历程图

对比图6、7可以看出，在切片谱法的方位历程图中，起始于102°方位的弱目标(记为目标A)轨迹清晰，可辨度高。常规的时域波束形成方法由于不能有效地抑制背景噪声，目标A被淹没在背景噪声之中，可辨识度低，未实现有效检测。

第10 s时的空间谱如图8所示：对于常规时域波束形成方法和切片谱算法均检测出来的35°、68°、138° 方向的目标，切片谱后置处理算法输出的信噪比要高于常规时域波束形成方法；另外，对于目标A，常规时域波束形成方法在目标A处无显著峰值，切片谱后置处理法在目标A处有显著峰值，可辨识性更强。

以上海试数据实验结果表明，本文提出的切片谱后置处理方法与常规方法相比，有效地提高了弱目标的检测信噪比，也通过实际数据验证了切片谱法在时域波束形成后置目标检测中应用的科学性和有效性。

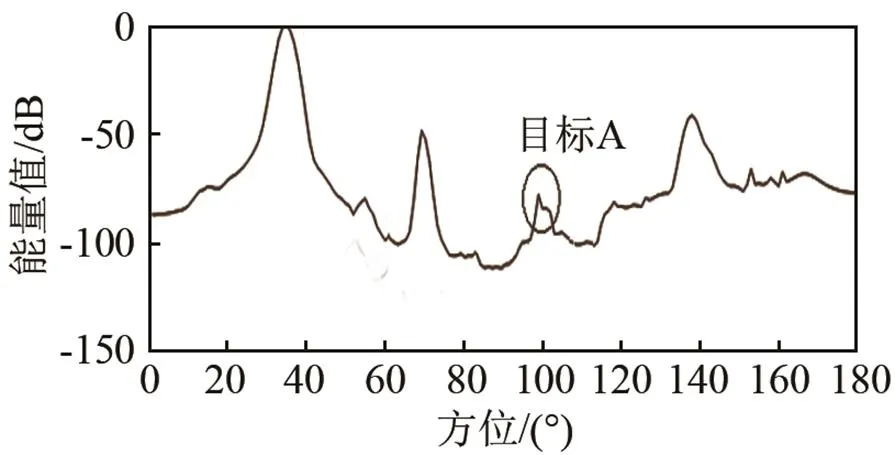
(a) 切片谱能量空间谱图

(b) 时域能量空间谱图

图8 海试数据的空间谱图

Fig.8 The spatial spectrums of actual sea trial data

5 结论

本文在理论推导切片谱后置处理算法的可行性后，采用仿真和海试数据验证了四阶累积量切片谱后置处理算法的科学性和有效性。仿真和海试数据结果均表明：在信噪比低于一定值的情况下，常规波束形成算法无法有效检测到弱目标时，后置处理算法可以有效检测到弱目标。

综上，本文后置处理算法相比常规时域波束形成算法，显著增强了抑制背景噪声的能力和弱目标检测的效果，但当目标位于预成波束的零陷方位时，需要再次进行预成波束处理，使某方位的波束内含低信噪比的目标信号，本方法才能见效。上述时域波束形成后置处理检测目标的思路和方法，可供深入研究甚低信噪比下有效检测目标时借鉴和参考。

[1] 张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 1999.

ZHANG Xianda. Morden signal processing[M]. Beijing: Tsinghua University Press, 1999.

[2] DOGAN M C, MENDEL J M. Application of cumulants to array processing-partⅠ: aperture extension and arraycalibration[J]. IEEE Trans SP, 1995, 43(5): 1200-1216.

[3] Li X K, JIA H J, YANG M. Underwater target detection based on fourth-order cumulant beamforming[C]//Proceedings of Meeting on the Acoustical Society of America, 2017, 31(1):109-118.

[4] 高杨, 李东生. 高阶累积量自适应波束形成的改进算法[J]. 火力与指挥控制, 2016, 41(3): 36-38, 47.

GAO Yang, LI Dongsheng. Improved adaptive beamforming algorithm based on higher order cumulant[J]. Fire Control and Command Control, 2016, 41(3): 36-38, 47.

[5] 伍岳, 张勇强. 基于高阶累积量的LCMV波束形成算法[J]. 无线电工程, 2013, 43(10): 19-21.

WU Yue, ZHANG Yongqiang. LCMV beamforming algorithm based on higher order cumulant[J]. Radio Engineering, 2013, 43(10): 19-21.

[6] 邓磊磊. 舰船辐射噪声的特征线谱提取[D]. 哈尔滨: 哈尔滨工程大学, 2011.

DENG Leilei. Characteristic line spectrum extraction from the ship-radiated noise[D]. Harbin: Harbin Engineering University, 2011.

[7] 冯西安, 黄建国. 基于四阶累积量切片的高分辨方位估计方法研究[J]. 系统工程与电子技术, 2001, 23(8): 1-3.

FENG Xian, HUANG Jian-guo. Research on high resolution methods of DOA estimation based on the slice of four-order cumulant[J]. Systems Engineering and Electronics, 2001, 23(8): 1-3.

[8] 郭业才. 基于高阶统计量的水下目标动态谱特征增强研究[D].西安: 西北工业大学,2003.

GUO Yecai. Research on High-order statistics based underwater moving target dynamic spectrum feature enhancement[D]. Xi’an: Northwestern Polytechnical University, 2003.

[9] 李长柏. 基于高阶谱和循环谱的舰船噪声多源特征分离研究[D]. 西安: 西北工业大学, 2005.

LI Changbo. Research on multi-resource seperation of ship noise based on high-order spectrum and cyclic spectrum[D]. Xi’an: Northwestern Polytechnical University, 2005.

[10] 张严, 王树勋. 非线性相位耦合的切片谱分析方法[J]. 电子学报, 1998, 21(10): 104-109.

ZHANG Yan, WANG Shuxun. Slice spectrum analysis method for nonlinear phase coupling[J]. Acta electronica sinica, 1998, 21(10): 104-109.

[11] 樊养余, 陶宝祺, 熊克, 等. 四阶累积量对角切片法提取舰船辐射噪声特征[J]. 声学学报, 2002, 27(5): 435-442.

PAN Yangyu, TAO Baoqi, XIONG Ke, et al. Characteristics of ship radiated noise extracted by four order cumulant diagonal slice method[J]. Acta Acustica, 2002, 27(5): 435-442.

[12] 包中华, 龚沈光, 吴正国, 等. 基于四阶累积量切片谱的谐波信号线谱提取[J]. 海军工程大学学报, 2010, 22(2): 31-34, 53.

BAO Zhonghua, GONG Shenguang, WU Zhengguo, et al. Spectrum extraction of harmonic signals based on four order cumulant slice spectrum[J]. Journal of Naval Engineering University, 2010, 22(2): 31-34, 53.

Object detection technology based on high-order spectrum of time domain beamforming signal

LI Lan-rui1, ZHANG Xin-hua1, LIU Hong-he2, LI Peng3, LIU Xin-yu4

(1. Department of Underwater Weapon and Chemistry Defense, Dalian Navy Academy, Dalian 116018, Liaoning, China; 2.Dalian Navy Area Equipment Repair and Maintenance Room, Dalian 116041, Liaoning, China; 3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150000, Heilongjiang, China; 4. Department of Political Training, Dalian Navy Academy, Dalian 116018, Liaoning, China)

In order to solve the problem of low noise suppress ability and poor detection ability of the conventional beam-forming (CBF) technology in weak target detection, the theory that the high-order cumulants of Gauss noise (three order and three order above) is zero and the non-Gauss signal is not zero, is used to process the beamforming signals after the CBF has been done. First, the fourth-order cumulant slice spectrum values of the time domain beamforming signals are calculated, and their square sum (i.e. energy superposition) is taken to obtain the spatial spectrum. Then, by accumulating the spatial spectrum in time, the azimuth time record is obtained. In this paper, both simulation data and actual data are used to verify the validity of the algorithm. It is found that the conventional algorithm cannot detecet the weak target effectively when the SNR decreases to a certain value, but the post processing algorithm can. The results show that the post processing algorithm after beamforming improves the ability of detecting weak targets and suppressing background noise.

time domain beamforming; fourth-order cumulant diagonal slice; object detection; high order spectrum

TB566

A

1000-3630(2018)-06-0540-05

10.16300/j.cnki.1000-3630.2018.06.005

2018-03-06;

2018-04-18

李兰瑞(1993－), 男, 山东聊城人, 硕士研究生, 研究方向为水声信号处理。

李兰瑞,E-mail:462488530@qq.com