水中规则波纹表面球回声特性研究
2019-01-11彭茜蕤周彦玲范军
彭茜蕤,周彦玲,范军
水中规则波纹表面球回声特性研究
彭茜蕤,周彦玲,范军
(上海交通大学海洋工程国家重点实验室,上海 200240)
运用声呐目标回声特性预报的板块元方法,研究了平面波入射水中规则波纹(正弦平方曲线波纹)表面球体的目标回声特性。分析了表面波纹高度、周期、入射平面波频率和入射方位角对声目标强度空间分布和频率响应特性的影响规律。讨论了不同频段目标强度空间分布特性的形成机理,得到了表面波纹参数与目标强度频率响应和空间分布特性的近似定量关系。通过水槽实验测量得到了3D打印的规则波纹表面尼龙球目标强度的频率响应和空间分布特性,测量结果与理论计算结果吻合较好。掌握规则波纹表面球体回声特性,有助于开展利用声学超构材料对散射声场调控的研究。
波纹表面;回声特性;目标强度
0 引言
粗糙表面声散射研究是一个既有理论意义又有实际意义的问题[1]。对粗糙表面回声(反向散射)特性的研究可应用于医疗超声、超声无损检测、海底和海面混响建模与抑制、海洋浮游生物分类和探测等方面。从Lord Rayleigh开始,对粗糙表面声散射已经进行了长期的研究。大多数水中粗糙表面声散射的研究都以起伏海底、海面声散射和混响建模为背景[2-4],针对粗糙平面声散射进行研究,其中,粗糙表面假设为满足高斯统计分布的随机起伏平面或正弦起伏平面。研究的方法包括Kirchhoff近似方法、基于瑞利假设的微扰方法、积分方程方法以及小斜率近似方法等。部分针对水下粗糙曲面目标声散射开展研究,T. K. Stanton针对水下浮游生物声散射,基于Sommerfeld-Watson变换和变形柱方法,研究了满足高斯统计分布的随机粗糙表面的拉长弹性柱体目标平均散射声场[5-7],P. Jansson基于从Helmholtz 积分方程推导得到的零场方法,研究了满足高斯统计分布的随机粗糙表面球形目标的声散射特性[8]。
确定性规则波纹(正弦波纹、正弦平方波纹只是其中的子类)表面目标是随机粗糙表面目标的一个特例,无论表面起伏幅度和斜率的大小程度如何改变,其散射声场总是相干的,这就使人们可以更为深入地研究粗糙表面目标的声散射特征,如J. A. Fawcett[9]采用Kirchhoff/衍射混合方法研究了具有正弦平方波纹起伏的刚性球和刚性圆柱的宽带脉冲信号声散射时域特征,但针对具有规则波纹表面的水下曲面目标声散射特性的研究较少。近年来,以目标表面微结构设计为基础的人工声学超材料的研究发现,表面规则波纹(狭缝)可以产生许多新的物理现象[10-11],如人工牛眼结构就是平面表面上由多个周期性同心凹槽组成的,这也可以看成是一类具有规则波纹结构的目标,这类人工牛眼声学结构可以引起声波异常透射和声波能量的单向传输。掌握规则波纹表面目标回声特性有助于开展利用声学超构材料对散射声场调控的研究。
本文应用声呐目标回声特性预报板块元方法,研究了平面波入射到水中规则波纹(正弦平方曲线波纹)表面(刚性和非刚性)实心球体目标的回声特性;分析了表面波纹高度、周期、入射平面波频率和入射方位角对声目标强度空间分布和频率响应特性的影响规律,讨论了不同频段目标强度空间分布特性的形成机理;并开展了3D打印的规则波纹表面尼龙球回声目标强度的频率响应和空间分布特性的水声水槽测量实验。
1 规则波纹表面球体目标
本文采用平面内满足式(1)的正弦平方波纹曲线绕轴旋转得到的三维规则波纹表面球作为典型目标开展研究,其表面方程见式(2)。




在计算仿真中假设表面具有以下两种声学特性[12-13],假设1是刚性表面,表面满足式(4)的刚性边界条件,假设2是非刚性表面,表面满足式(5)的边界条件:



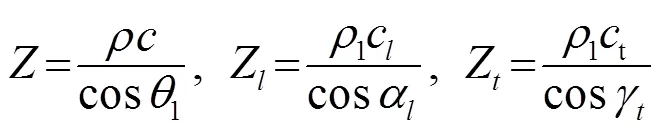
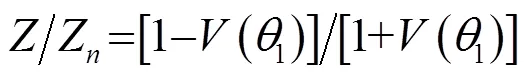
2 回声特性预报的板块元方法
基于Kirchhoff 近似所建立的板块元方法是一种相对较为成熟的对声呐目标中高频回声特性进行预报的数值方法[12]。对于收-发合置的情况,基于物理声学或Kirchhoff 近似的非刚性声呐目标的远场目标强度(TS)为[13]


板块元方法首先将目标的三维几何表面进行空间板块离散划分,用一组三维平面板块来近似复杂形状的目标曲面,一般采用三角形板块进行划分。所有板块的散射声场之和就是总散射声场的近似值。算法中将单个三维板块变化到局部二维平面,式(10)中的面积分则转化为与板块顶点坐标相关的代数运算,如式(11)所示,从而避免了面积分运算,提高了计算速度。

假如划分为个平面板块,则式(10)可以写成:

板块元方法比通常的面元积分法计算速度快,不仅适用于远场、刚性目标的回声特性预报,还可推广应用于近场和非刚性表面的回声特性预报,目前板块元方法已经较为广泛应用于声呐目标中高频回声特性预报[15-18]。
本文将采用板块元方法对规则波纹表面球回声特性进行仿真计算,需要说明的是目前考虑的波纹球波纹起伏相对较小,计算中忽略了声波在波纹凹槽之间的多次散射[19-20]。
3 数值计算与分析
以正弦平方波纹球为例,采用板块元方法对其回声特性进行数值仿真。波纹球的半径=0.3 m,在仿真中假设球面为刚性边界条件。
3.1 目标强度的频率响应特性

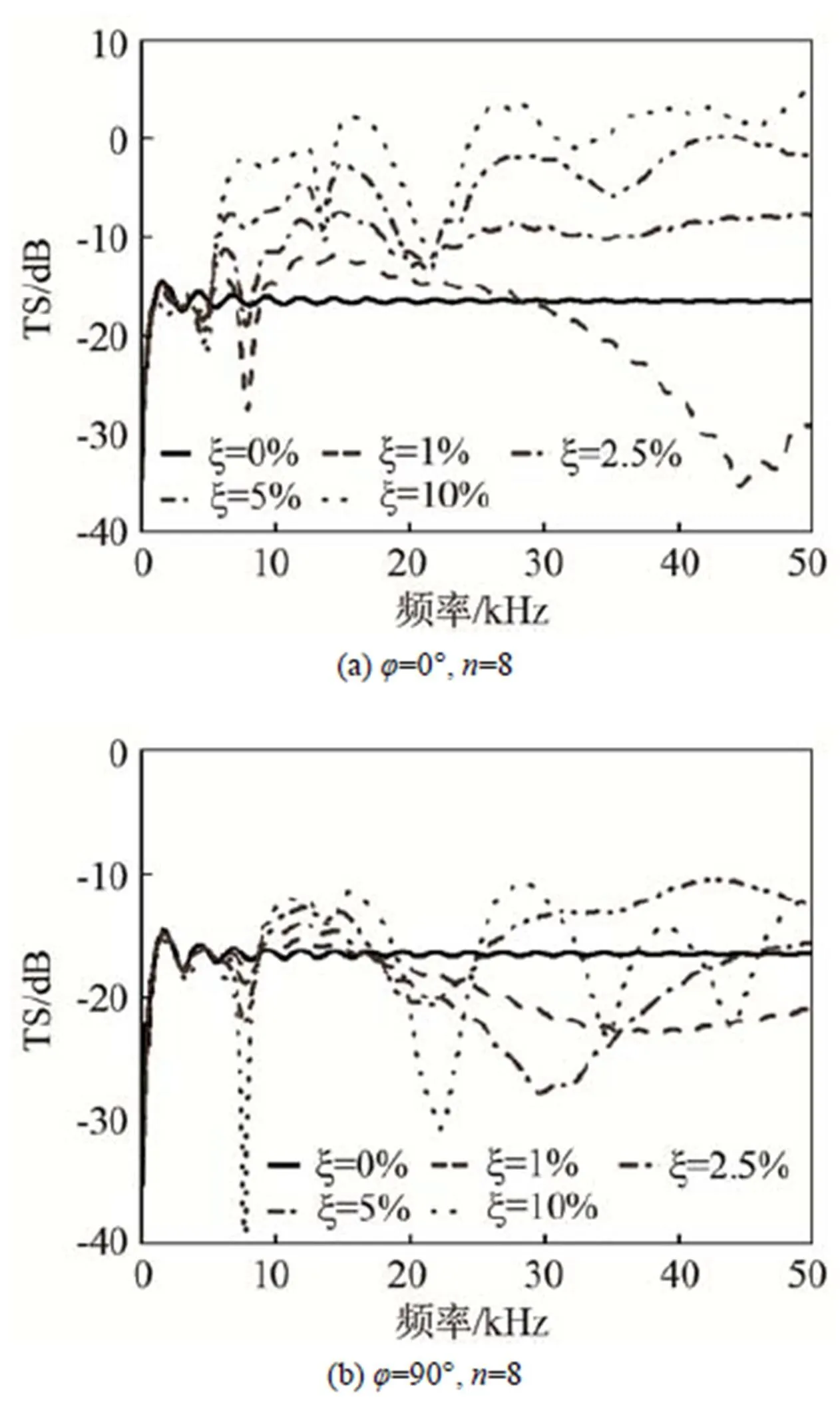
图2 不同ξ条件下的波纹球目标强度频率响应(a) φ=0°;(b) φ=90°
3.2 目标强度的空间分布特性

图3 波纹球目标强度的空间分布特性
由图3可以看出,在低频(2 kHz)处波纹球目标强度的空间分布基本是均匀的,如图中虚线所示,接近光滑球的目标强度空间分布,即波纹效应没有体现。随着频率的升高,波纹球目标强度随入射角变化呈现“花瓣状”峰谷空间分布,并且频率越高“花瓣状”峰谷结构分支越密集。相对来说,=8的波纹球目标强度呈现的“花瓣状”峰谷分支结构比=5的更为密集。
值得注意的是,当频率升高到波纹效应呈现的频段,目标强度“花瓣状”峰谷空间分布的峰谷与波纹球表面波纹的峰/凹槽结构基本对应。并且随着频率升高到不同的频段,目标强度“花瓣状”分支峰谷结构对应表面波纹结构的不同部分。图4为=8的波纹球局部放大图。

图4 表面波纹局部结构

按如下原则得到频段划分近似公式:


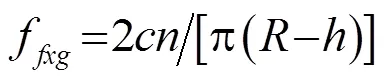

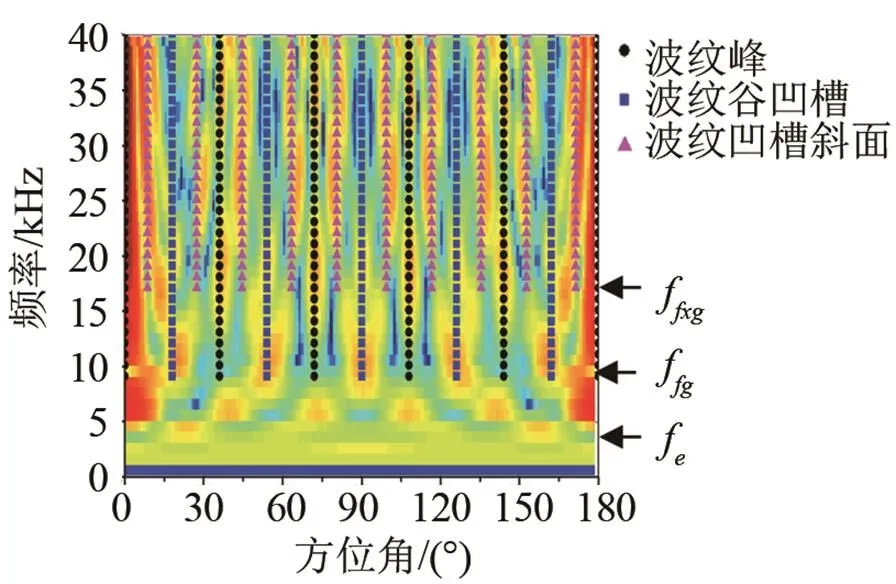
图5 频率-角度谱
因正弦平方波纹球具有局部多镜面反射(波峰、谷凹槽、凹槽斜线),使得其散射声场在空间形成多峰结构,这种多峰结构与入射波频率、入射角度紧密相关,可以通过调整表面波纹周期、起伏幅度对散射声场的空间分布特性进行调控。
4 声散射实验
4.1 实验布局

图6 3D打印的波纹实验模型和实验布置图
4.2 实验数据分析
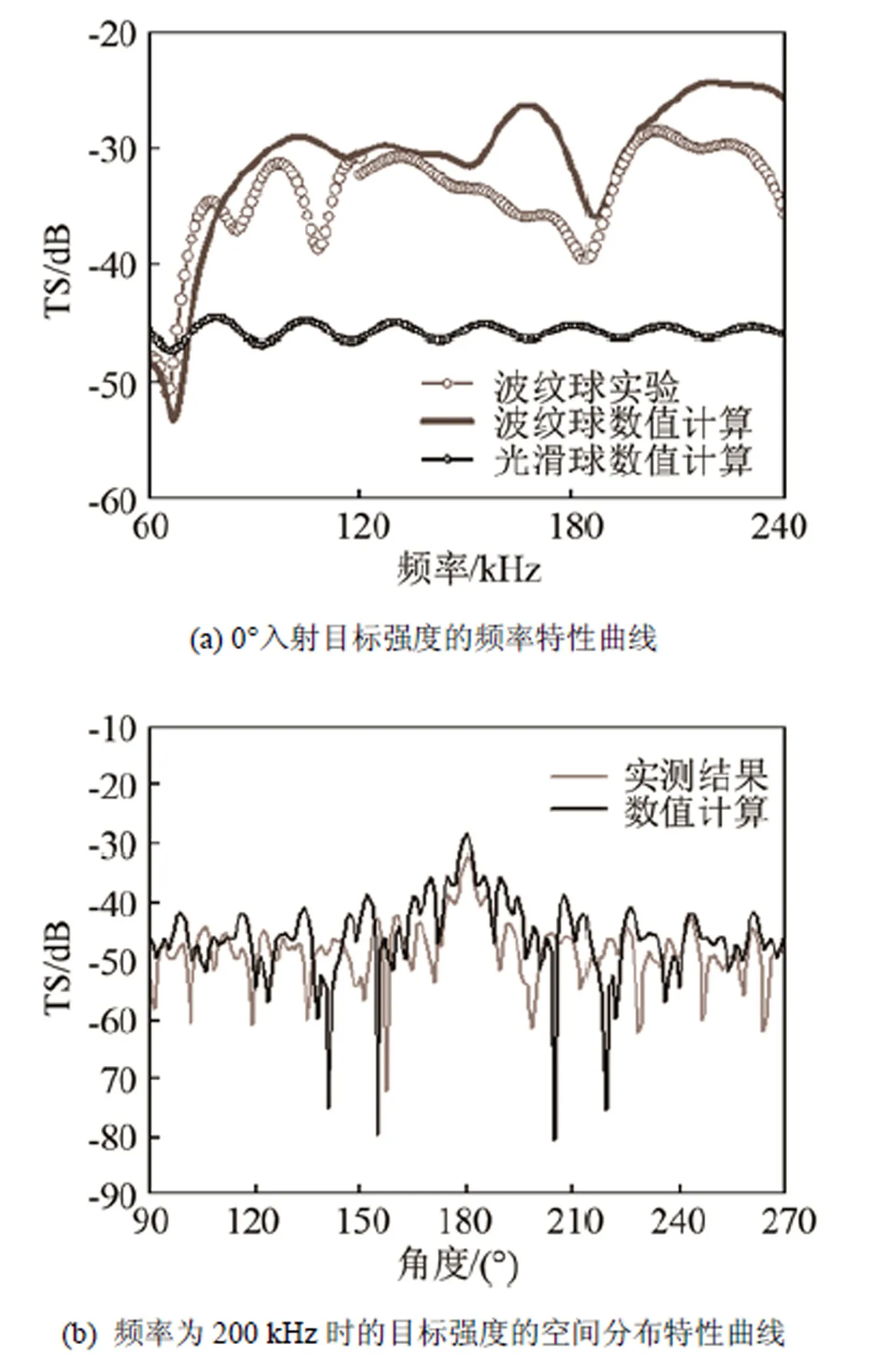
图7 目标强度的实验与数值计算结果对比
5 结论
通过板块元数值计算和实验,研究了平面波入射水中规则波纹(正弦平方曲线波纹)表面球体的目标回声特性。结果表明:低频时波纹高度、周期对声目标强度基本没有影响,随着频率的升高,多镜面反射(波峰、波谷凹槽和凹槽斜面)的影响清晰显示出来,且波纹高度越高和周期越大,声目标强度起伏越大、峰值越密集。通过水槽实验测量得到了3D打印的规则波纹表面尼龙球目标强度的频率响应和空间分布特性,测量结果与数值计算结果吻合较好。规则波纹表面球体回声特性的掌握有助于开展利用声学超构材料对散射声场调控的研究。
[1] OGILVY J A. Theory of wave scattering from random rough surfaces[M]. Bristol: Hilger, 1991.
[2] JACKSON D R, RICHARDSON M D. High-frequency seafloor acoustics[M]. New York: Springer, 2007.
[3] WELTON P J. Three dimensional analyses of scattering by pressure release sinusoidal surfaces[J]. J. Acoust. Soc. Am., 2012, 131 (1): 54-68.
[4] CHOO Y M, SONG H C, SEONG W J. Numerical study of three-dimensional sound reflection from corrugated surface waves [J]. J. Acoust. Soc. Am., 2016, 140(4): 2290-2296.
[5] STANTON T K. Sound scattering by rough elongated elastic objects. I: Means of scattered field[J]. J. Acoust. Soc. Am., 1992, 92(3): 1641-1664.
[6] STANTON T K, CHU D. Sound scattering by rough elongated elastic objects. II: Fluctuations of scattered field[J]. J. Acoust. Soc. Am., 1992, 92(3): 1665-1678.
[7] GURLEY J V, STANTON T K. Sound scattering by rough elongated elastic objects. III. Experiment[J]. J. Acoust. Soc. Am., 1993, 94(5): 2746-2755.
[8] JANSSON P. Acoustic scattering from a rough sphere[J]. J. Acoust. Soc. Am., 1993, 93 (6): 3032–3042.
[9] FAWCETT J A. Modeling of high-frequency scattering from objects using a hybrid Kirchhoff/diffraction[J]. J. Acoust. Soc. Am., 2001, 109(4): 1312-1319.
[10] MEI J, HOU B, KE M Z, et al. Acoustic wave transmission through a bull’s eye structure[J]. Appl Phys Lett, 2008, 92: 1-3.
[11] WANG J W, YUAN B G, CHENG Y, et al. Unidirectional acoustic transmission in asymmetric bull’s eye structure[J]. 2015, 58(2): 1-5.
[12] 范军, 汤渭霖, 卓琳凯. 声呐目标回波特性预报的板块元方法[J].船舶力学, 2012, 16(1-2): 171-180.
FAN Jun, TANG Weilin, ZHUO Linkai. Planar elements method for forecasting the echo characteristics from sonar targets[J]. Journal of Ship Mechanics, 2012, 16(1-2): 171-180.
[13] 汤渭霖. 用物理声学方法计算非硬表面的声散射[J]. 声学学报, 1993, 18(1): 45-53.
TANG Weilin. Calculation of acoustic scattering of a nonrigid sur- face using physical acoustic method[J]. Acta Acustica, 1993, 18(1): 45-53.
[14] 布列霍夫斯基赫著. 分层介质中的波[M]. 杨训仁译. 北京: 科学出版社: 1960.
BREKHOVSKIKH L. Wave in layered medium[M]. YANG Xunren, translate. Beijing: Science Press: 1960.
[15] 邓伟, 范军. 基于鱼雷导引弹道的目标回声特性研究[J]. 声学技术, 2014, 33(5): 402-407.
DENG Wei, FAN Jun. Research on target echo characteristics in torpedo guidance trajectory[J]. Technical Acoustics, 2014, 33(5): 402-407.
[16] 卜考英, 范军. 基于多波束系统的水下目标近程回波亮点声图像[J].声学技术, 2007, 26(4): 570-573.
BU Kaoyin, FAN Jun. Acoustic image of bright spots of near-field underwater targets based on multi-beam system[J]. Technical Acoustics, 2007, 26(4): 570-573.
[17] 王二庆, 卓琳凯, 王华奎. 单双层壳体潜艇的高频回波特性研究[J].声学技术, 2012, 31(5): 486-489.
WANG Erqing, ZHUO Linkai, WANG Huakui. High-frequency echo characteristics of single and double shell submarine[J]. Technical Acoustics, 2012, 31(5): 486-489.
[18] 王汝夯, 李冰, 魏强. 基于板块元的水面舰船远场声目标强度预报方法[J].声学技术, 2015, 34(1): 6-10.
WANG Ruhang, LI Bing, WEI Qiang. A method for predicting far-field target strength of surface ship based on planar elements theory[J]. Technical Acoustics, 2015, 34(1): 6-10.
[19] 郑国垠, 范军, 汤渭霖. 考虑遮挡和二次散射的修正板块元算法[J]. 声学学报, 2011, 36(4): 377-383.
ZHENG Guoyin, FAN Jun, TANG Weilin. A modified planar elements method considering occlusion and secondary scattering[J]. Acta Acustica, 2011, 36(4): 377-383.
[20] 张阳, 李桂娟, 王振山, 等. 改进的板块元遮挡算法[J]. 声学技术, 2016, 35(4): 319-324.
ZHANG Yang, LI Guijuan, WANG Zhenshan, et al. An improved plate element sheltering algorithm[J]. Technical Acoustics, 2016, 35(4): 319-324.
[21] 刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 1993.
LIU Bosheng, LEI Jiayu. Principles of underwater acoustics[M]. Harbin:Harbin Engineering University Press, 1993.
Echo characteristics of a regular corrugated surface ball in water
PENG Xi-rui, ZHOU Yan-ling, FAN Jun
(State Key Laboratory of Ocean Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
Echo characteristics of a regular corrugated (sine squared curve) surface sphere in water with an incident plane wave are investigated by using the planar elements method which is used for forecasting echo characteristics of sonar targets. The effects of surface corrugation’s height, period, incident plane wave frequency and incident azimuth angle on the spatial distribution and frequency response characteristics of acoustic target strength are analyzed. The formation mechanism of the spatial distribution characteristics of target strength in different frequency bands is discussed. The approximate quantitative relationship between the parameters of corrugated surface and the spatial distribution as well as the frequency response characteristics of target strength is obtained. The target strength of the 3D printed regular corrugated surface nylon sphere is measured in acoustic tank. The measured spatial distribution and frequency response characteristics of target strength are in good agreement with the theoretical results. A thorough understanding of the echo characteristics of regular corrugated surface sphere is helpful for conducting research on controlling the scattering sound field by using the acoustic metamaterials.
corrugated surface;echo characteristics; target strength
TB556
A
1000-3630(2018)-06-0528-07
10.16300/j.cnki.1000-3630.2018.06.003
2017-12-13;
2018-03-15
国家自然科学基金(11774229)资助项目。
彭茜蕤(1993-), 女, 湖北武汉人, 硕士, 研究方向为水下目标声散射。
范军,E-mail: fanjun@sjtu.edu.cn
