阵列测量中的卡尔曼滤波器算法
2019-01-11季建朝张宇赵子龙夏露
季建朝,张宇,赵子龙,夏露
阵列测量中的卡尔曼滤波器算法
季建朝1,2,张宇2,赵子龙2,夏露2
(1. 清华大学航天航空学院,北京 100084;2. 陆军航空兵学院,北京 101123)
针对经典波束形成算法不具备实时性、占用存储空间大、计算速度慢等缺点,提出了基于卡尔曼滤波器的算法。这种算法将信号处理领域中现有的卡尔曼滤波器理论与阵列信号处理过程相结合,在频域内对声学阵列所采集到的数据进行迭代处理,不仅能够及时发现风洞测量中存在的各种问题,而且可以实时消除由测量环境所引起的各种误差。仿真结果表明,这种算法比经典波束形成算法收敛速度更快,不仅成像效果很好,而且能够对低速运动声源进行定位。此算法具备实时性,为风洞声源的实时定位提供了重要的算法选择。
气动噪声;阵列信号处理;波束形成;迭代方程
0 引言
随着交通运输、工业生产、城市建筑等的快速发展,噪声污染日益严重。长期处于强噪声环境,会给人的生理、心理带来很大危害,因此,噪声污染、大气污染和水污染一并被称为世界三大污染。为了降低噪声的影响,需要设计出相应的噪声控制方案,而方案的设计依赖于准确定位噪声源的分布和估算其强度。近些年,基于声传感器阵列的噪声源辨识测量应用与研究正变得越来越广泛[1-2]。
阵列信号处理算法主要是波束形成算法,包括将采集数据进行延时相加的经典算法[3]、具有较强点声源分辨能力的逆向法[4]、能够显著提高声源分辨率的反卷积算法[5],以及有效提高旁瓣抑制能力、减小虚假声源干扰的算法[6]等。经典算法由于其稳定性和普适性,目前应用最为普遍。然而,经典算法不具备实时性,不能对运动或者旋转声源进行定位,并且生成的图像分辨率偏低,虽然可通过增大阵列直径,增加阵列单元数来提高分辨率,但需要处理庞大的实验数据才能分离出信号源。随着处理数据的增加,经典算法表现出越来越多的局限性,比如:需要的数据存储空间大,收敛速度慢等。此外,在将阵列技术推广到运动声源定位的过程中,需要对声源到声传感器之间的传递函数进行修正,采用修正后的传递函数对测量信号进行重构,得到准确测量结果[7]。但对于运动轨迹未知且运动轨迹复杂的声源,处理起来有一定难度,而且在时域内修正会付出较大计算代价。特别是在声源运动速度较慢,多普勒效应影响不大的情况下,修正后的结果与未修正的结果区别不大,一味进行修正耗费很大的计算量,结果改善却不明显。
为了解决经典算法对整体测量数据的依赖和低速声源在定位过程中遇到的问题,本文提出了一种基于卡尔曼滤波器的算法,其基本思想来自信号处理领域的卡尔曼滤波器理论,并与阵列噪声测量过程相结合,将整个噪声检测过程视为利用卡尔曼滤波器进行时间和空间的滤波过程。关于滤波估计声源状态的思想,在文献[8-9]中也有体现。本文应用卡尔曼滤波器算法进行了单极子成像、实时性能方面的数值模拟和实验验证,并将其结果与经典算法进行了比对。结果表明:对于固定声源,卡尔曼滤波器算法收敛速度快,成像效果好;对于某些运动速度不快、运动轨迹复杂的声源,不仅可以实现实时定位,而且计算量也较小。
1 经典算法


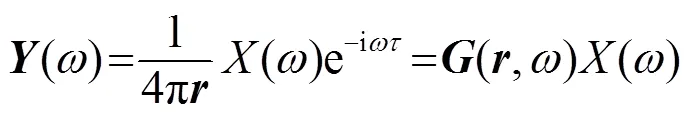
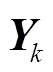

式(3)的解为:
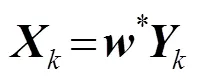


2 卡尔曼滤波器算法

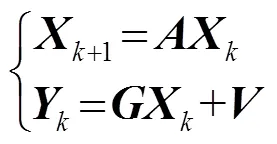
式(7)中的状态更新矩阵A可通过图1进行说明:由于声源X为稳态信号,在状态更新过程中,数据的频谱信息也是稳定的,因此A为单位矩阵[12]。为通道噪声,假设其符合高斯白噪声分布,均值为零,方差为。
对于系统方程(7)可设计卡尔曼滤波器进行状态估计。
状态更新方程为


测量更新方程为
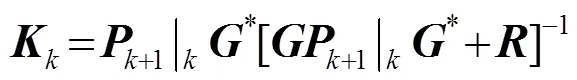

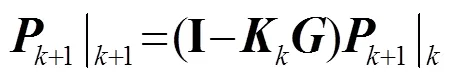
需要特别指出得是:式(7)~(12)并非仅能代表同窗数据,可以根据测量需求进行扩展。例如:在去除背景噪声过程中,可将式(7)中的状态分别理解为背景噪声、信号源,输出理解为背景噪声输出、背景噪声加信号源输出。然后再按照式(8)~(12)迭代计算,去除背景噪声,获得声源状态。
3 仿真计算
3.1 点源成像

图2(a)和图2(b)分别显示了经典算法前20个数据块和卡尔曼滤波器算法第10个数据块结果,其中经典算法未进行谱交叉矩阵优化。可以看到,在第10个数据块时,建立在对声源状态递归估计基础上的卡尔曼滤波器算法就基本能够达到未经优化的经典算法前20个数据块时的效果,收敛速度明显高于经典算法,而且主瓣动态范围较高,旁瓣抑制效果也较为明显。
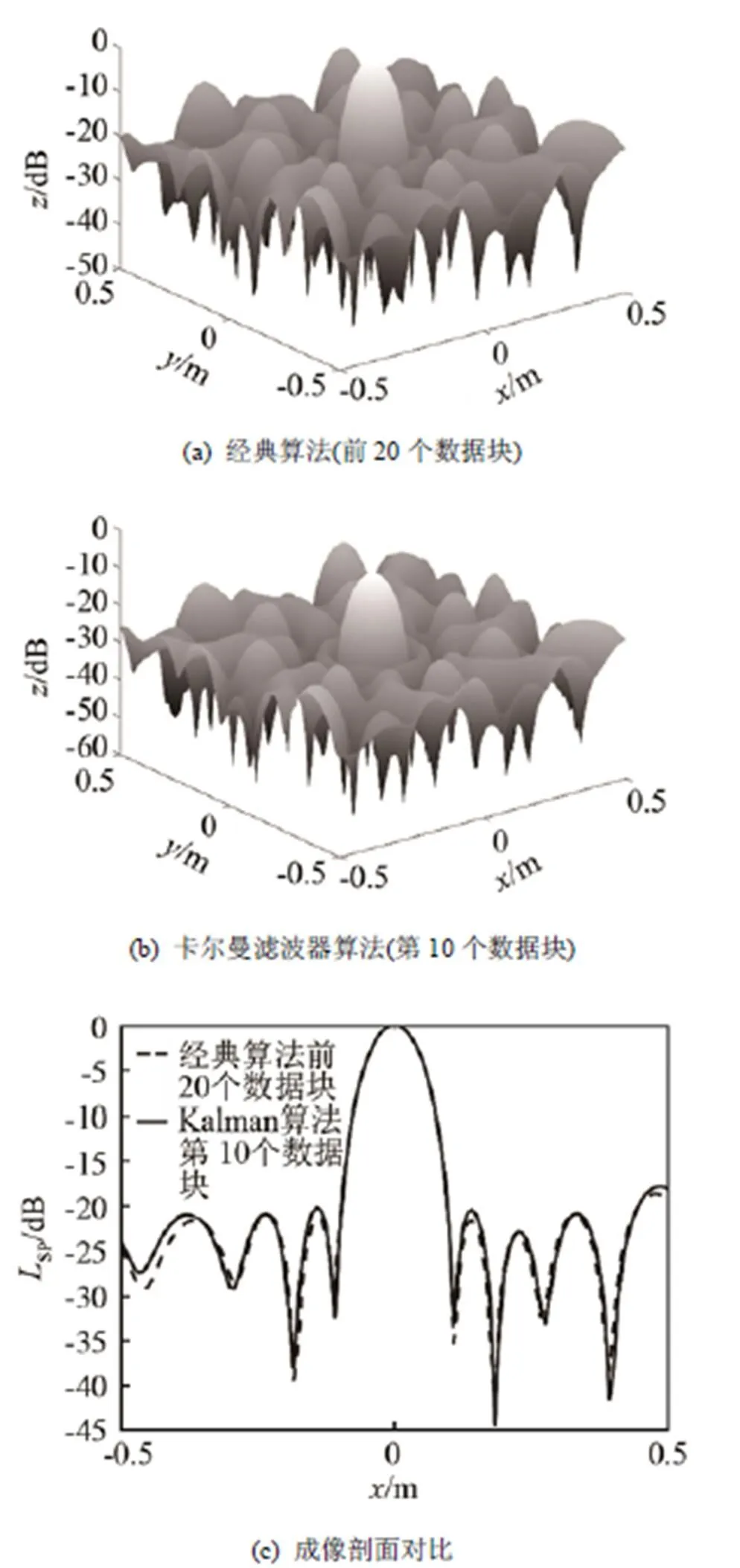
图2 经典算法和卡尔曼滤波器算法单极子成像对比
以上分析表明,卡尔曼滤波器算法在数据迭代过程中收敛更加迅速,可快速得出结果;另外,声源波束形成动态范围大、准确性高,成像结果令人满意。
3.2 实时能力验证
图3为运动声源测量示意图,边长为1 m的正方形阵列中包含56个声传感器,声传感器按照多臂螺旋线排列,在距离阵列0.7 m的平面上设置一个点声源,点声源按照正弦曲线运动,运动轨迹与阵列平行,曲线的幅值为0.3 m,波长为0.6 m,曲线中心位置与阵列中心线重合,其它参数与图2相同。由于声源距离阵列平面较近,运动速度不快,声源运动所产生的零点误差和漂移误差很小,简单起见,在成像结果中忽略多普勒效应(对成像结果几乎没有影响),没有对声场进行重建,在实际测量中要对测量精度和计算量进行权衡而定。

图3 运动声源测量示意图
图4为经典算法对运动声源的成像结果,动态范围显示15 dB。其中,图4(a)~4(d)分别为前25个、50个、75个和100个数据块结果,图中箭头代表声源的运动方向。可以看到,随着声源的运动,整个轨迹上都出现了声压分布,没有准确定位到声源的实时位置,其原因就在于经典算法是基于统计-平均的思想,将采集到的数据离线统一处理,所有数据具有同等权重,这种处理方式不仅占用了运算资源、浪费了存储空间,而且当测量设备出现问题时也不能及时发现,只能再次进行测量。因此,不具备实时性成为经典算法的一个缺陷。
图5为卡尔曼滤波器算法对运动声源的成像结果,其中,图5(a)~5(d)分别为第25个、50个、75个和100个数据块结果。显然,该算法实时、准确定位了运动声源的位置。在计算过程中采用的数据块长度为4 096,如果适当缩短数据块长度,实时性能还会有所增加,数据块长度的选择可根据待测声源的运动速度进行调节。对数据块进行迭代处理,使得卡尔曼滤波器算法计算量较小,对运算资源和存储空间的占用也较低,能够及时发现在测量过程中存在的问题,最主要的是这种算法具备了实时性,能够准确定位运动声源的位置。
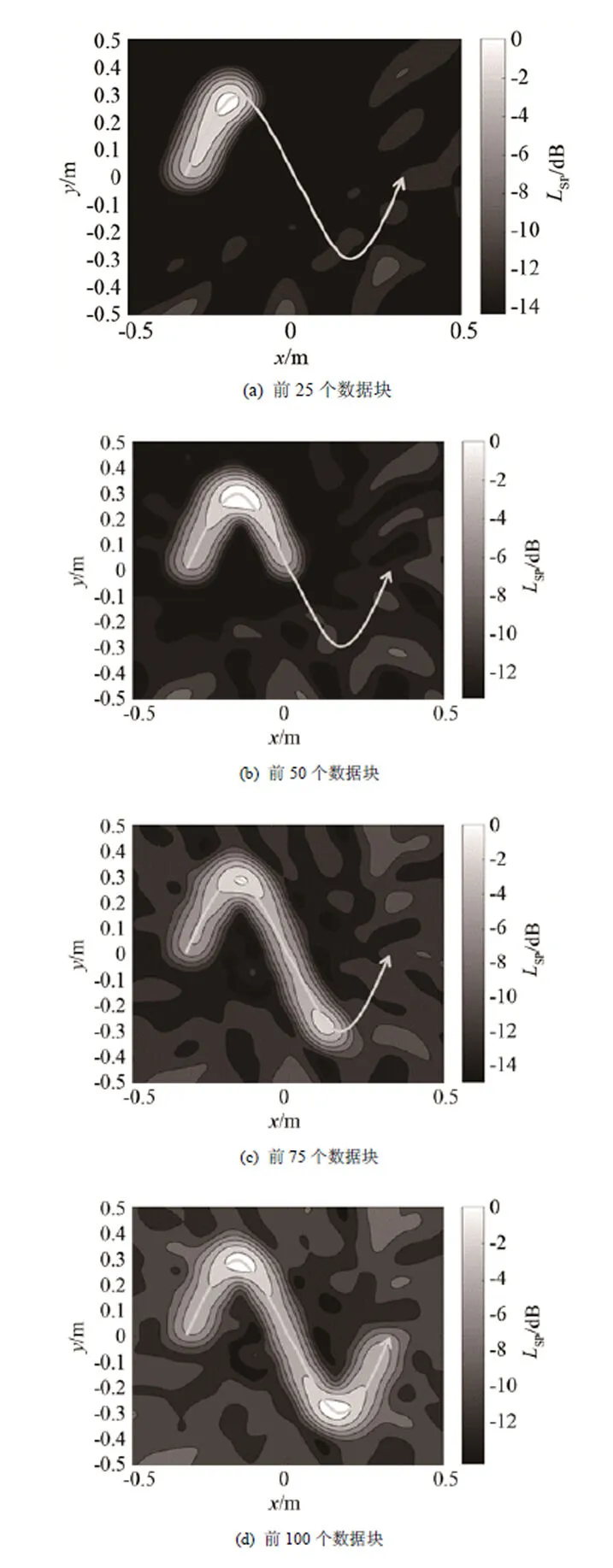
图4 经典算法运动声源成像

图5 卡尔曼滤波器算法运动声源成像
4 实验验证
为了验证卡尔曼滤波器算法的准确性,在实验室内进行了如图6所示的双点声源定位实验,图中两个小音箱模拟单极子声源,频率均为3 kHz,距离阵列平面0.5 m,阵列含有56个通道,按照多臂螺旋线排列,采样频率48 kHz,数据块长度为4 096。
图7和图8分别展示了经典算法和卡尔曼滤波器算法对于双点声源成像的结果,可以看到在第1个数据块时,经典算法结果与卡尔曼滤波器算法结果基本没有差别,但随着处理数据块的增加,卡尔曼滤波器算法收敛更快,到第10个数据块时,其结果已经优于了经典算法,原因就在于卡尔曼滤波器对新信息的权重更大,在对声源状态进行估计时,将更快速地接近于真实值。

图6 双点源阵列成像实验

图7 经典算法计算双点声源

图8 卡尔曼滤波器算法计算双点声源
5 结论
使用阵列进行气动声源测量时,要根据测量对象和成像要求选择不同的算法。本文从状态估计角度提出了基于卡尔曼滤波器的算法,在频域内对阵列采集数据进行迭代处理,估计系统状态。仿真结果表明,该方法不仅能够准确定位固定声源,而且能够跟踪某些运动声源,实现实时定位。通过分析可以得到以下结论:
(1) 对于固定声源,经典算法对所有数据进行统计-平均,结果较为稳定;对于状态变化的声源,采用基于卡尔曼滤波器的算法,不仅能够消除测量误差,而且能够实时显示声源状态。
(2) 卡尔曼滤波器算法具有强大的实时数据处理能力,适合于某些运动轨迹较为复杂、运动速度慢、离阵列平面近的声源,收敛速度快,节约了运算和存储成本,声源成像动态范围大。
(3) 在缩短数据块长度、提高实时性的过程中,如何提高卡尔曼滤波器算法分辨率需要进一步研究;另外,卡尔曼滤波器算法是在频域内进行的迭代运算,如何将算法发展到时域,加入多普勒效应修正也是今后研究的重点。
[1] MOREAU D J, DOOLAN C J, ALEXANDER W N, et al. Wall-mounted finite airfoil-noise production and prediction[J]. Aiaa Journal, 2016, 54(5): 1637-1651.
[2] 季建朝, 王明新, 周永清. 闭口风洞声学测量中的阵列设计[J]. 声学技术, 2018, 37(2): 99~104.
JI Jianchao, WANG Mingxin, ZHOU Yongqing. Array design for acoustic measurement in closed wind tunnel[J]. Technical Acoustics, 2018, 37(2): 99-104.
[3] VEEN B D V, BUCKLEY K M. Buckley. Beamforming: a versatile approach to spatial filtering[J]. IEEE ASSP Mag, 1988, 5(2): 4-24.
[4] LI S, XU Z, HE Y, et al. Generalized inverse beamforming via elastic net regularization[J]. Chinese Journal of Scientific Instrument, 2015, 36(5): 1170-1176.
[5] 杨洋, 褚志刚, 江洪,等. 反卷积DAMAS2波束形成声源识别研究[J]. 仪器仪表学报, 2013, 34(8): 1779-1786.
YANG Yang, CHU Zhigang, JIANG Hong, et al. Research on DAMAS2 beamforming sound source identification[J]. Chinese Journal of Scientific Instrument, 2013, 34(8): 1779-1786.
[6] 李征初, 李勇, 陈正武, 等. CLEAN-SC算法在风洞声源定位与识别中的应用研究[J]. 实验流体力学, 2016, 30(3): 104-109.
LI Zhengchu, LI Yong, CHEN Zhengwu, et al. Noise identification and localization in wind tunnel using CLEAN-SC algorithm[J]. Journal of Experiments in Fluid Mechanics, 2016, 30(3): 104-109.
[7] 张杰. 基于麦克风平面阵列的运动噪声源定位及算法研究[D]. 杭州: 中国计量学院, 2014.
ZHANG Jie. Research on Moving Noise Source Localization Methods Based on Plane Microphone Array[D]. Hangzhou: China Jiliang University, 2014.
[8] HUANG X. Real-time algorithm for acoustic imaging with a microphone array[J]. J. Acoust. Soc. Am., 2009, 125(5): 190-195.
[9] HUANG X, VINOGRADOV I, BAI L, et al. Observer for phased microphone array signal processing with nonlinear output[J]. Aiaa Journal, 2010, 48(11): 2702-2705.
[10] 季建朝, 张宇, 王明新. 声传感器阵列风洞测量结果优化[J]. 清华大学学报(自然科学版), 2018, 58(1): 94-100. JI Jianchao, ZHANG Yu, WANG Mingxin. Optimization of acoustic sensor arrays for wind tunnel measurements[J]. Journal of Tsinghua University(Science and Technology), 2018, 58(1): 94-100.
[11] MUELLER T J. Aeroacoustic measurements[M]. Berlin Heidelberg: Springer,2002: 66-67.
[12] PEEBLES P Z. Probability, random variables, and random signal principles[M]. New york: McGraw-Hill, 1987.
[13] BURNSIDE N, JAEGER S, REINERO B, et al. Array design and performance for a large scale airframe noise study[C]//8th AIAA/CEAS Aeroacoustics Conference & Exhibit. 2002: 2576.
[14] JAEGER S, HORNE W, ALLEN C. Effect of surface treatment on array microphone self-noise[C]//6th Aeroacoustics Conference and Exhibit. 2000: 1937.
Kalman filter-based algorithm for acoustic array measurement
JI Jian-chao1,2, ZHANG Yu2, ZHAO Zi-long2, XIA Lu2
(1. College of Aeronautics and Astronautics, Tsinghua University, Beijing 100084, China; 2. Army Aviation Institute, Beijing 101123, China)
The conventional beamforming (CB) is the most popular signal processing technique for noise identification using acoustic sensor arrays. However, CB does not have real-time performance and takes up a lot of storage space, the calculation speed is slow. A new approach called Kalman filter based beamforming method is introduced in this paper, which has a recursive form similar to Kalman filter in signal processing field. The data collected by acoustic array are processed iteratively in frequency domain, it can not only detect various problems in the wind tunnel survey, but also eliminate the errors caused by the test environment in real time. The simulation results show that the algorithm converges faster than the CB algorithm, the imaging results is very good, more importantly, it can accurately locate some low speed moving sound sources. This algorithm runs in real-time, so it is an attractive new algorithm for the real-time localization of wind tunnel sound source.
aeroacoustics; array processing; beamforming; recursive functions
V211.71
A
1000-3630(2018)-06-0601-06
10.16300/j.cnki.1000-3630.2018.06.016
2017-11-27;
2018-02-05
国家自然科学基金(11402305)资助项目。
季建朝(1981-), 男, 河北保定人, 博士, 讲师, 研究方向为声学测量、声学控制。
季建朝, E-mail: jianchao_ji@163.com
