超声切削加工的声系统阻抗匹配问题研究

孔立阳，胡小平，于保华，刘东海



超声切削加工的声系统阻抗匹配问题研究

孔立阳，胡小平，于保华，刘东海

(杭州电子科技大学机械学院，浙江杭州 310018)

匹配电路作为超声发生器的电系统与声系统的传输纽带，其设计的好坏决定了整个超声加工系统的工作性能。基于实验，分析了匹配电路元件的不同连接方式对声系统性能的影响；提出了基于最小功率点与能量传输效率综合最优的匹配方式与原则，并验证了此种匹配方式能大幅提升切削加工的稳定性。为同类超声加工工艺的匹配电路参数的选取和声系统性能优化提供了依据。

声学系统；能量传输；最小功率点；稳定

0 引言

随着科技的飞速发展，超声技术在加工领域得到了越来越广泛的应用。超声切削加工的工作原理主要是由超声波发生器产生电信号，经由换能器将电能转变为机械能，经过变幅杆增大振幅，最后加载到刀具上切削材料[1]。通常将换能器、变幅杆和切削刀具作为整体，视为超声波发生器的声学负载系统，在这两者之间需要设计匹配电路。芳纶蜂窝材料的正交各向异性和非连续分布的特性，使超声加工过程中声学系统的切削力负载具有时变性。切削力负载的变化导致声学系统的谐振频率、等效阻抗和品质因数等参数发生明显变化，影响声学系统的谐振状态与能量的利用效率。作为匹配电路，不仅要实现调谐、滤波和变阻功能，还必须保证整个超声系统具有良好的转换效率和传输效率。

超声加工声学系统应用在不同的领域中，对换能器的各参数要求也不尽相同。结合各自的超声技术应用领域，国内外研究学者对匹配技术开展了一系列的研究工作。鲍善惠等[2]对压电换能器在并联谐振频率附近的特性进行了研究；J Y Moon等[3]提出一种基于通用滤波器结构的新型电阻抗匹配(EIM)电路，用以扩大高频超声波换能器的频谱带宽并提高信噪比；Y Z YIN等[4]提出了一种结合信号频率和电感调节的换能器匹配方法，通过识别最大电流值并引用锁相环频率跟踪技术，提高了动态调谐效率。

本文通过实验，研究电容、电感不同的连接方式和取值对声学系统各参数的影响。分析其规律并结合实际加工要求，确定合适的匹配电路。基于空载时输出功率最小的最佳匹配点与能量传输效率综合最优，确定匹配原则。实验验证本文设计的匹配电路与原则，能够提高功率的利用效率，刀具振幅稳定，满足切削要求。这对于工业应用中如何提高功率因数、优化品质因数、减少设备损耗有着重要的参考意义。

1 声学系统等效电路

超声加工过程中广泛应用的换能器，由极化的压电陶瓷片叠加装配而成，利用压电材料的逆压电效应将电信号转变为机械振动。变幅杆与刀具一般视作纯阻性负载，而压电换能器等效的电学特性一般呈容性。对超声波发生器而言，包含换能器、变幅杆和工具等的声学系统相当于一个容性负载。对一个容性负载而言，它的电流超前于电压，功率因数不为1。提高功率因数可以提高输出功率的利用率，减少传输线路的功率损耗。因此，如何在超声发生器和声学系统之间建立合适的匹配电路，使声学系统作为整体负载的阻抗虚部为0，保障电源系统和声学系统之间高效地能量传输，在超声加工领域具有重要的意义。

在串联谐振点，声学系统的阻抗最小，相当于一个效率达到极值的发射器。而工作在并联谐振频率附近时，声学系统的阻抗达到最大值，可以看作一个效率最高的接收器。超声切削时，希望以最小的能量得到理想的刀具振幅，获得较高的能量转换效率。因此本文选择阻抗较小、发射效率较高的串联谐振频率作为工作频率进行分析。

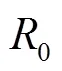
串联谐振频率为

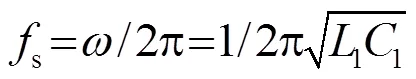
2 匹配电路设计

由于超声发生器属于开关型电源，输出电压中含有丰富的噪声成分，且输出电流越大，噪声成分也越大，这将影响声学系统两端电压波形的质量[5]。因此，单一的电感匹配虽然从电学角度上可以达到声学系统纯阻的目的，但还不能起到较好的滤波效果。一般会加入电容元件来增强滤波效果，保证声学系统具有良好的振型。

2.1 匹配元件影响分析

匹配声学系统本身作为一个谐振系统，连接大小不同的电容、电感元件会对其本身的谐振频率等阻抗特性产生不同的影响。在设计匹配电路时，不仅要考虑到滤波、调谐和变阻的功能，能量的转换与传输效率也是一个重要的参考量。

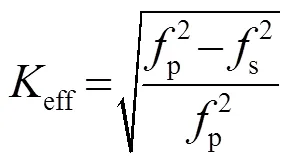
品质因数是表示振子阻尼性质的物理量，其值反映压电材料的机械损耗大小，越高表示能量损失速率越慢，越低表示在能量传输过程中损失越大，因此在谐振频率附近振幅也就较小，不过具有较宽的谐振带宽。品质因数可以表示为[6]

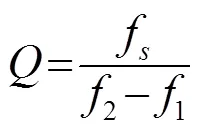
为了选择匹配电路中储能元件的类型和串、并联的连接方式，搭建了阻抗分析实验台，如图2所示。调节自制的匹配箱，将电容、电感以不同大小和方式分别接入等效电路，用阻抗分析仪测量匹配后声学系统的参数值。与未匹配时声学系统相关参数进行比较，分析匹配电路对声学系统性能的影响规律，并根据实际情况选择合适的匹配方式。

图2 阻抗分析的实验装置

用于超声切削的声学系统参数变化如表1所示。对比表1中数据可以看出：

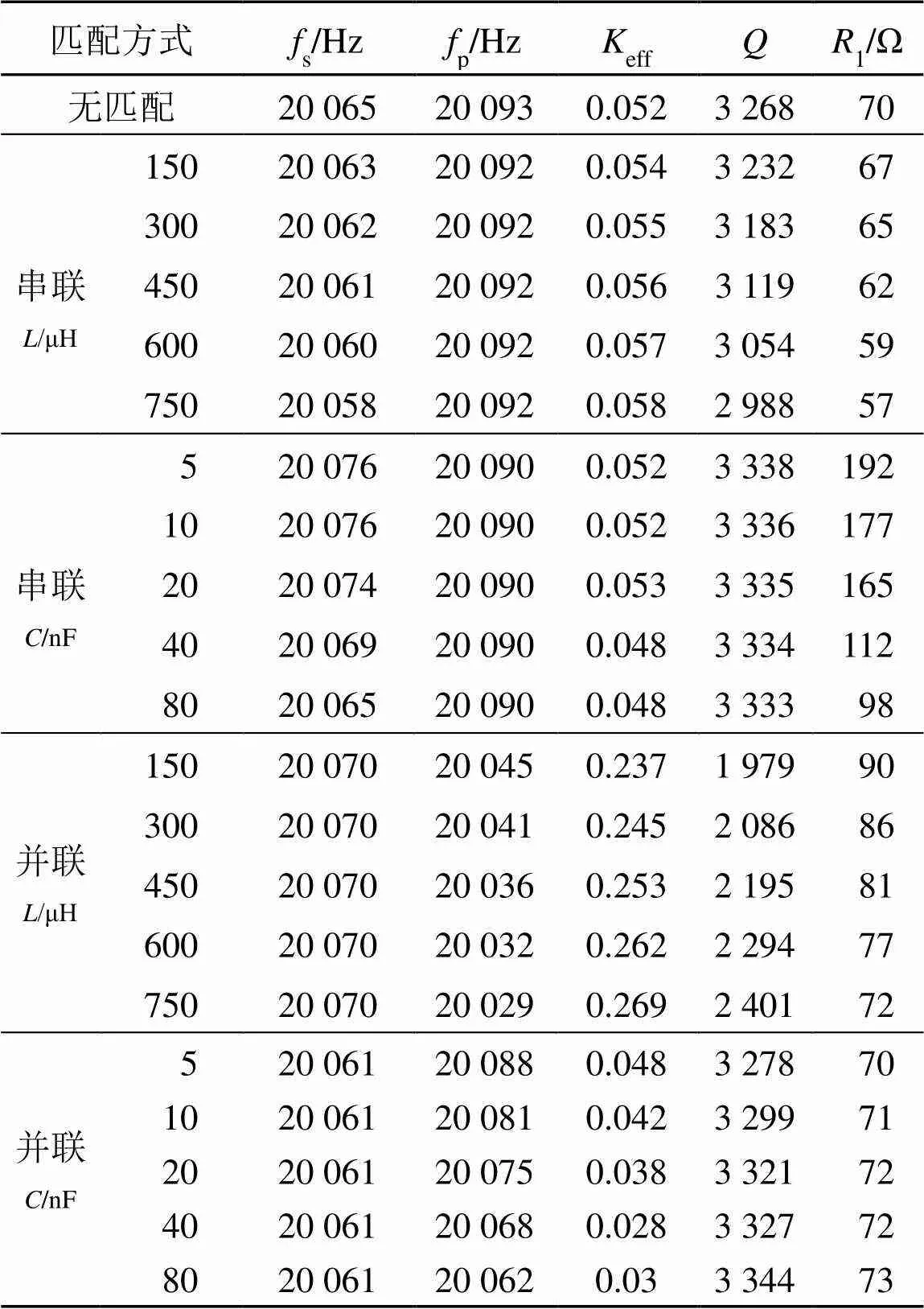
表1 用于超声切削的声学系统参数变化表

(1) 对于两个谐振频率而言，以串联方式接入电容或电感只影响串联谐振频率值，同理并联连接只影响并联谐振频率大小；

(2) 电容的接入相比电感的接入不仅增大了滤波的效果，对的提高也有较好的作用。相较于并联电容，串联电容虽然可以增大值，但动态电阻也大大增加。这将增大无用功损耗，因此不选择串联电容的方式；

(4) 串联电感虽然在一定程度上降低了，但减小幅度并不大，这意味着串联电感在有限程度内增大了能量的损耗。但的增大使能量的利用率增加，且的减小意味着谐振带宽会有一定增加，这有利于超声加工的稳定性。

由上可知，串联电感和并联电容对声学系统有积极的作用。LC混联匹配方式不仅可以增大电路的滤波效果，满足电抗相消特性，而且可以满足减小动态电阻、减少能量损耗、优化能量传输的功能。LC混联匹配下的等效电路如图3所示。

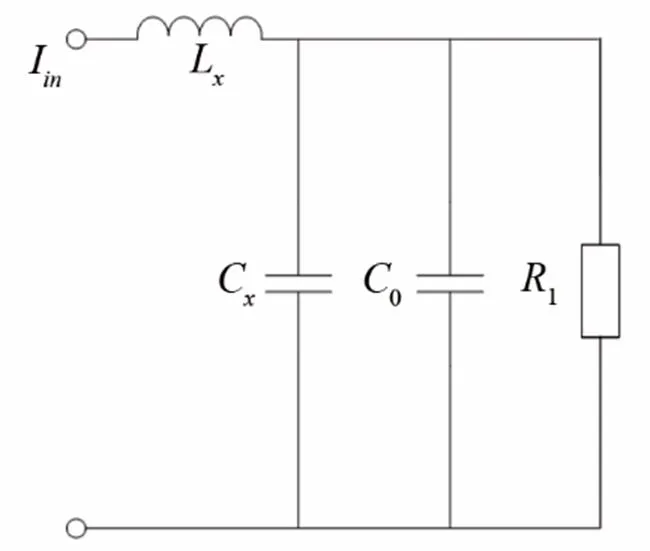
图3 LC混联匹配下的等效电路

2.2 设计匹配原则

静态匹配时，不考虑力载荷对声学系统等效参数的影响，根据未受力状态下的动态电阻、谐振频率、静电容等计算得到匹配电感、电容的值。力负载的作用会使声学系统的动态电阻大幅度增大，谐振频率等参数也会发生明显变化，使匹配电路难以达到效果，能量的传输效率大大降低。即不考虑力负载时得到的匹配电路，在空载时是匹配最佳的点，振动状态最好。加工过程中时变性的力负载减弱了匹配电路调谐变阻的效果，导致声学系统切削性能远低于空载状态[7]。针对这种情况，一般措施是增大电源输出功率，使力负载作用下减小的振幅和功率仍能保持在一个较高的值，保证切削性能。但是这种方式会产生大量功率损耗，且空载下振幅过大容易导致刀具断裂。

超声切削芳纶蜂窝材料过程中，刀具未进入材料时，即处于空载状态，应使电源的输出功率最小。刀具正常切削时，力负载使声学系统整体的阻抗增大，此时电源的输出功率应该随之增大，以避免刀具振幅的下降影响切削效果。利用匹配电路调谐变阻的功能，选择合适的匹配参数，将电源系统的输出功率匹配到最佳值，使电源输出功率在力负载的作用下也可以保持相对稳定。

整个超声切削系统的阻抗可以表示为[8]

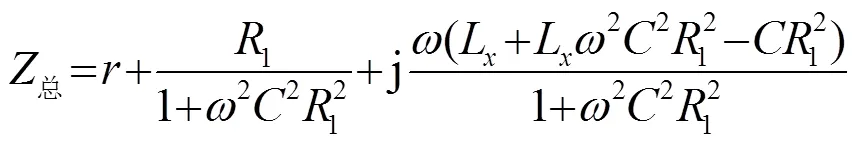
匹配后声学系统呈纯阻状态，即阻抗虚部为0，则匹配电感应满足：

设电源输出电压幅值为，总电流为

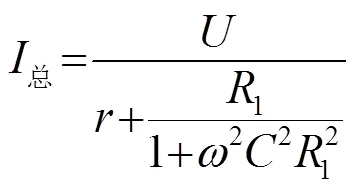
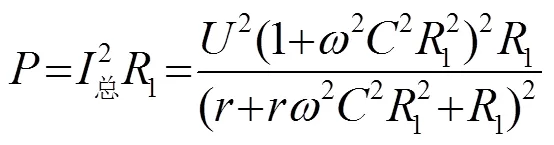
本文选择在空载时，声学系统以最小的功率输出，而在加工过程中能得到更高的功率，以适应因力负载作用而增大的阻抗，维持振幅稳定。因此对取极小值：

式(9)中各参数值都大于0，若要保证功率最小，则应满足：

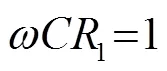
综上所述，在计算匹配元件的参数时，应满足以下原则：满足声学系统谐振要求；整体阻抗虚部为零；功率输出的相对稳定性。即：

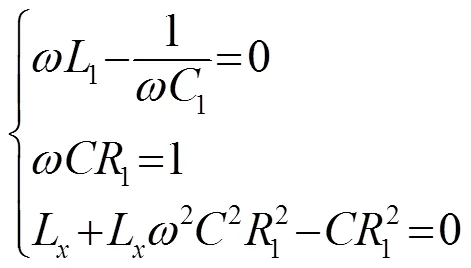
3 实验验证

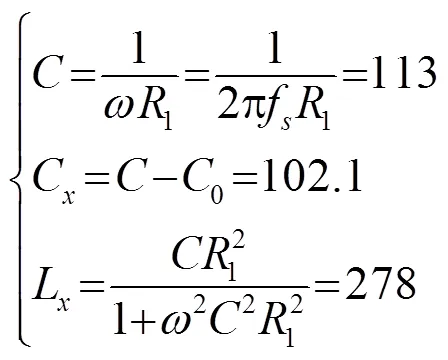
为测试本文设计的匹配电路对声学系统振动性能的作用效果，搭建了测量振幅的实验台，如图4所示。泰克信号发生器和1140LA射频功率放大器模拟超声发生器产生超声频信号。自制的匹配箱按照计算得出的匹配参数进行调节，作为匹配电路，LO-Z-12-DH变压器完成变阻匹配的功能。利用HP-50数字显示式推拉力计给声学系统上的刀具施加力，模拟切削过程中的力负载。用KEYENCE激光位移传感器测量刀具的振幅大小。

施加不同大小的力，会造成声学系统谐振频率不同程度的偏移。调节信号发生器的输出频率，直到射频放大器上显示的无功功率为最小值，记录此时的频率值和相应的刀尖振幅。

要将声学系统匹配成纯阻状态，串联一个电感元件就能完成。但是不能很好地适应切削时不断变化的阻抗参数，匹配效果减弱[9]。本文设计的LC匹配电路与匹配原则，在静态最小功率点进行匹配，能较好地提升加工过程中的切削性能。图5记录了声学系统在单电感匹配与LC匹配后，力负载变化对其频率与振幅的影响。由图5可知：

(1) 单电感匹配的声学系统在力负载的作用下，频率漂移严重，容易造成失谐，影响切削性能。LC匹配的频率变化幅度较小，相对稳定。

(2) 单电感匹配时，随着力负载增大，振幅下降明显，切削效果变差，材料界面容易破裂。LC匹配下的声学系统振幅较为稳定，能保证良好的切削效果。

(3) 单电感匹配在零负载时振幅最大，切削过程中均不是最佳切削状态。LC匹配时，零负载的振幅最小，不仅能使芳纶蜂窝材料在切削过程中保持良好的切削性能，而且降低了空载时的功率损耗，减小了刀具被崩断的危险。

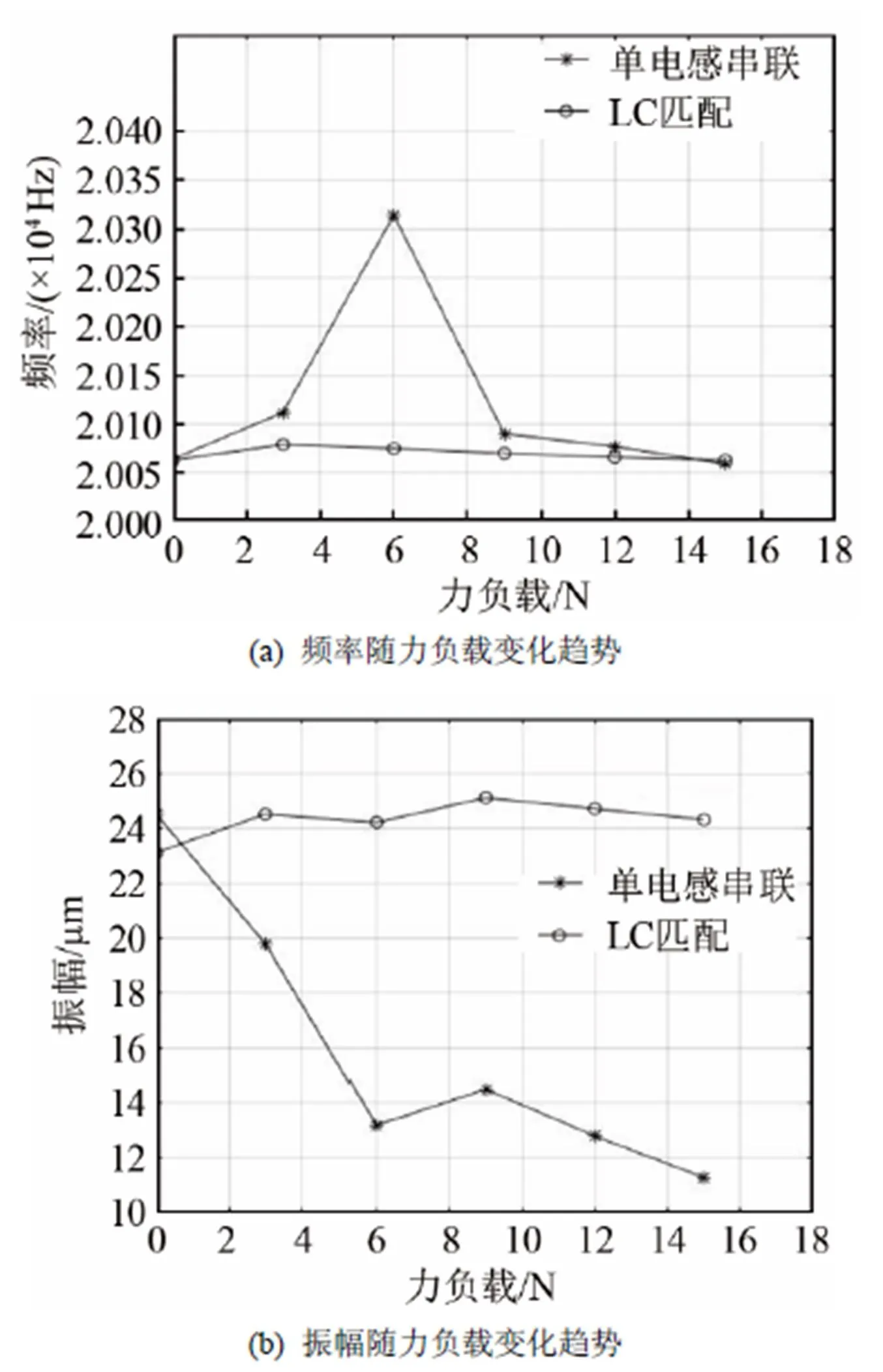
图5 超声切削系统中单电感和LC匹配后频率振幅测量

4 结束语

文章分析了不同匹配元件及其连接方式对声学系统的影响，确定了匹配电路。提出空载时最小功率点的匹配方式，并给出匹配参数的计算原则。图5的实验结果表明，LC匹配方式对提高切削稳定性、保证切削效果确实有效。

本文将压电换能器、变幅杆、刀具看作一个整体进行分析。但换能器作为机电转换元件可以分为电端和机械端。电端正是本文中的电子元件与超声发生器之间的相连部分，由匹配电路对其进行优化。机械端为换能器与变幅杆、刀具相连部分，变幅杆形状、刀具长短等参数对声学系统的影响未作考虑，后续研究可从该方面考虑进行优化。

[1] 张云电. 超声加工及其应用[M]. 北京: 国防工业出版社, 1995.

ZHANG Yundian. Ultrasonic processing and its application[M]. Beijing: National Defence Industry Press, 1995.

[2] 鲍善惠, 王艳东. 压电换能器在并联谐振附近特性的研究[J]. 声学技术, 2006, 25(2): 165-168.

BAO Shanhui, WANG Yandong. Study on the characteristics of piezoelectric transducers in parallel resonance[J]. Technical Acoustics, 2006, 25(2): 165-168.

[3] MOON J Y, LEE J S, CHANG J H. Electrical impedance matching networks based on filter structures for high frequency ultrasound transducers[J]. Sensors and Actuators, 2016, 251: 225-233.

[4] YIN Y Z, ZHU C P. A transducer matching method with signal frequency and inductor adjustment combined for submerged structure ultrasonic cleaning[J]. Mechatronics and Industrial Informatics II, 2014, 596: 704-708.

[5] 韩丽轩, 于保华, 胡小平. 功率超声压电换能器阻抗匹配电路参数化设计[J]. 压电与声光, 2015, 37(4): 713-716.

HAN Lixuan, YU Baohua, HU Xiaoping. Parametric design of impedance matching circuit for power ultrasonic piezoelectric transducer[J]. Piezoelectrics & Sound, 2015, 37(4): 713-716.

[6] SHOH A. Welding of thermoplastics by ultrasound[J]. Ultrasonics, 1976, 14(9): 209-217.

[7] 蒋辊林. 压电换能器匹配电路的设计[J]. 电声技术, 2012, 36(9): 26-29.

JIANG Gunlin. Design of piezoelectric transducer matching circuit[J]. Electron Sound Technology, 2012, 36(9): 26-29.

[8] 胡隽璇. 新型铝合金超声铸造电源的研究与设计[D]. 长沙: 中南大学, 2011.

HU Junxuan. Research and design of new aluminum alloy ultrasonic casting power supply[D]. Changsha: Central South University, 2011.

[9] 孙波, 季远, 李光军, 等. 功率超声换能器导纳特性检测及电端匹配研究[J]. 振动、测试与诊断, 2002, 22(4): 287-290.

SUN Bo, JI Yuan, LI Guangjun, et al. Study on admittance characteristic detection and electric end matching of power ultrasonic transducer[J]. Journal of Vibration, Testing and Diagnosis, 2002, 22(4): 287-290.

Research on the impedance matching of acoustic system in ultrasonic cutting operation

KONG Li-yang, HU Xiao-ping, YU Bao-hua, LIU Dong-hai

(School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou 310018, Zhejiang, China)

As the matching circuit is the transmission link between electrical system and acoustic system of ultrasonic generator, the design of matching circuit greatly affects the performance of acoustic system. Based on experiments, the influences of the connection modes of matching circuit components on the performance of acoustic system are analyzed. Then, a matching method, which is based on the optimal combination of the minimum power point with the energy transmission efficiency, is put forward. The experimental results show that the matching method can greatly improve the stability in ultrasonic cutting operation. Besides, it provides a basis for the selection of matching circuit parameters and the optimization of acoustic system performance in similar ultrasonic machining process.

acoustic system; energy transmission; minimum power point; stability

TB559

A

1000-3630(2018)-06-0560-05

10.16300/j.cnki.1000-3630.2018.06.009

2017-09-04;

2017-12-04

国家自然科学基金(51475130)资助项目

孔立阳(1994－), 男, 浙江杭州人, 硕士研究生, 研究方向为特种加工超声电源。

胡小平,E-mail: xiaoping.hu@hdu.edu.cn