利用插值余项证明含导数的一类不等式
2019-01-11李娜
李 娜
构造辅助函数来证明不等式是高等数学中的一种重要思想方法,有关构造辅助函数的方法十分丰富,并且有一定的技巧性,没有固定的模式和方法,插值法的思想是根据有限个点的坐标或是导数结果来构造一个简单的多项式函数p(x),其实就是用p(x)来逼近要研究的函数f(x),此法有章可循,且有统一的公式,本文利用插值法的公式可以简洁地证明一类含导数的不等式。
1 预备知识

定义2. 若在区间[a,b]上用Ln(x)近似f(x),则其截断误差为Rn(x)=f(x)-Ln(x),也称为插值多项式的余项。关于插值余项估计有以下定理。
定理1. 设f(n)(x)在[a,b]上连续,f(n+1)(x)在(a,b)内存在,设ax0 其中ξ∈(a,b),记ωn+1(x)=(x-x0)(x-x1)…(x-xn)。 Rn(x) 特别地,当n=1时,拉格朗日插值多项式称为线性插值,它的余项为 当n=2时,拉格朗日插值多项式称为抛物线插值,它的余项为 例 设f(x)∈C2a,b且f(a)=f(b)=0,求证: 其中C2a,b表示在区间a,b上二阶导数连续的函数空间。 法1: 由于要证一具体点满足某个不等式,且题中所涉函数具有二阶或二阶以上连续导数,容易联想到泰勒公式. 证明如下: 分别将x=a,x=b代入上式,得 (2) 将(1),(2)相加,又f(a)=f(b)=0,得 有 · 通过上述证明过程可以看出,利用泰勒公式证明该类型题,需要根据已知条件先判断在哪个具体位置进行泰勒展开,很灵活,有一定的技巧性,不易掌握,完整的证明出来需要系统地掌握高等数学知识。 法2:根据公式,已知两点(a,f(a))及(b,f(b)),代入公式,得到线性插值多项式为 因为函数f(x)在区间a,b上二阶连续可导, 且题目待证的不等式包含x的二阶导,我们利用插值余项构造辅助函数f(x)-L1(x), 又因为(x-a)(x-b)=(a-x)(x-b), 当且仅当取等号 又已知f(a)=f(b)=0,所以有 在已知条件中含有一个或几个点上的函数值或者导数值以及高阶导数值,研究函数或它的各阶导数满足的性质这类问题,我们可以考虑用插值思想构造插值多项式,此法有公式可依,容易操作,可以简洁地完成证明。
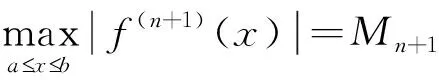


2 证明一类含导数不等式举例



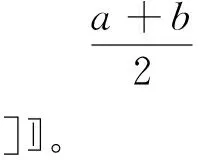
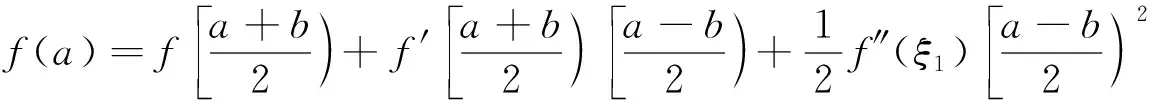


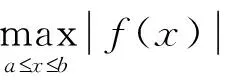


3 结 语
