基于改进滑模观测器的锂离子电池荷电状态估计方法

隋 欣， 陈永翀， 张晓虎， 刘丹丹

(1. 中国科学院电工研究所， 北京 100190；2. 中国科学院大学， 北京 100049)

1 引言

电动汽车是一种新能源汽车，使用电能作为能量来源，节能、环保，逐渐受到了人们的重视[1，2]。电池作为电动汽车的关键部件，对整车系统的动力性、安全性以及经济性至关重要[3]。为了有效防止电池的过充和过放，延长电池的使用寿命，最大限度地保证电池的安全可靠运行，需要对电池的荷电状态(State of Charge, SOC)进行准确估计[4，5]。

锂离子电池是一个非线性电化学系统，荷电状态和内部参数无法直接测量，因此需要进行辨识研究，文献中提出多种SOC估计方法。安培法依赖于SOC的初值，且因噪声和测量误差的影响，估计误差会逐渐累积[6]。开路电压法[7]充分利用电池OCV-SOC关系，但需要长时间静置，无法应用于实时估计，并且有些锂电池如磷酸铁锂、钛酸锂等在SOC中间区域存在电压平台区，无法准确估计SOC。电化学阻抗谱法需要对电池施加一系列小电流信号，进行多频段信号激励，由于电池的电化学特性对阻抗谱有很强的影响，可通过检测电池响应得到内部阻抗。由于低频不满足短时测量的要求，该方法只能在高频区进行且仅适用于特定的充电条件。此外需要增加多余装置来提供正弦源，因此该方法不适用于电动汽车的在线应用[8]。智能算法包括神经网络和模糊算法等将电池看作黑箱系统，在无需知道电池内部结构的前提下，通过大量训练数据对系统进行准确估计，但是增加了电池管理系统的计算量，应用受到限制[9，10]。为了对锂电池SOC进行实时估计，许多学者提出基于模型的估计方法[11-19]。主要原理是给定输入信号，通过当前时刻和上一时刻的状态量以及模型参数得到输出量的估计值，将输出量的误差作为反馈，对估计状态量进行迭代运算。这类方法包括基于卡尔曼滤波器[11，12]、龙贝格观测器[13]、H∞观测器[14，15]和滑模观测器[16-18]的SOC估计算法。

扩展卡尔曼滤波器通过一阶泰勒展开，将非线性方程线性化，但局部线性化会引入很大误差[11]。自适应Sigma卡尔曼观测器按非线性模型对状态变量的分布构建Sigma采样序列，采用模型输出残差更新噪声协方差，赋予Sigma采样序列最优估计及噪声的权值，并实现误差量的实时更新[12]。卡尔曼滤波算法是龙贝格观测器[13]的优化算法，这两种方法都需要进行复杂的矩阵运算，导致低成本单片机上实现困难。此外方法的准确性严重依赖于模型和传感器精度，且受线性化精度和雅可比矩阵稳定性的制约，任何模型和噪声协方差的不精确性都可能降低滤波器性能，导致收敛速度降低。H∞理论是限制外源扰动对输出影响的有力工具，基于该方法的SOC估计目的是抑制系统范数和测量噪声干扰，对电池的状态量具有很强的鲁棒性，但是和卡尔曼滤波算法有同样的计算复杂的缺陷，且饱和度等非线性约束处理不当会影响模型精度[14，15]。

锂离子电池是一个复杂的化学系统，模型参数易受电池性能差异和运行环境的干扰，对其内部状态量进行观测，需要构建一个抗干扰性强的观测器。滑模观测器的滑模面通过变结构开关高频率切换，使状态的运动点保持在一个平面上，最终趋近于稳定。基于该观测器的SOC估计算法对参数变化和系统扰动不敏感，在SOC初值已知和未知的情况下，仅利用测量的电流、电压值便可以高精度地估计SOC，且计算量小，适合复杂运行工况[16-18]。对于滑模变结构系统来说，希望状态变量能尽快达到切换面，同时保证状态点达到切换面的速度不能过大，否则将引起系统的抖振。传统的滑模观测器由于采用离散开关函数引入高频分量，不可避免的存在抖振现象。

为了解决上述问题，提出一种基于改进滑模观测器(Improved Sliding Mode Observer，ISMO)的SOC估计方法。用sigmoid函数代替符号函数，有效缓解了传统滑模观测器(Conventional Sliding Mode Observer，CSMO)存在的抖振问题。此外，引入系统辨识理论中带噪声的滑动平均模型，将预报误差法的思想应用于锂离子电池模型参数辨识，增强了算法的抗噪声能力。将得到的一阶RC模型参数随SOC的变化进行在线更新，从而进一步提高估计精度。分别在美国城市道路工况(Urban Dynamometer Driving Schedule, UDDS)循环工况和混合充放电工况下对电池进行测试，实验结果表明，与传统滑模观测器相比，提出的方法能有效削弱抖振，消除模型误差，具有较高的SOC估计精度和鲁棒性。

2 锂离子电池建模

锂离子电池常用的等效电路模型包括阻抗模型、Rint模型，Randles模型、戴维南模型、RC模型以及PNGV模型等[19，20]。这些模型复杂性和准确性各不相同，但是经过星-三角变换和模型阶数选择，可以互相推导得到，在某种程度上互相等效[21]。荷电状态估计的准确性很大程度上依赖于准确可靠的电池模型，但是过分追求模型的准确性会增加计算的复杂性和计算量。通过建立电池的ARMAX模型，采用预报误差法对模型未知参数进行辨识，抗噪声能力强，辨识结果准确。同时构建改进滑模观测器，进一步消除模型误差。使用的一阶RC等效电路模型如图1所示。

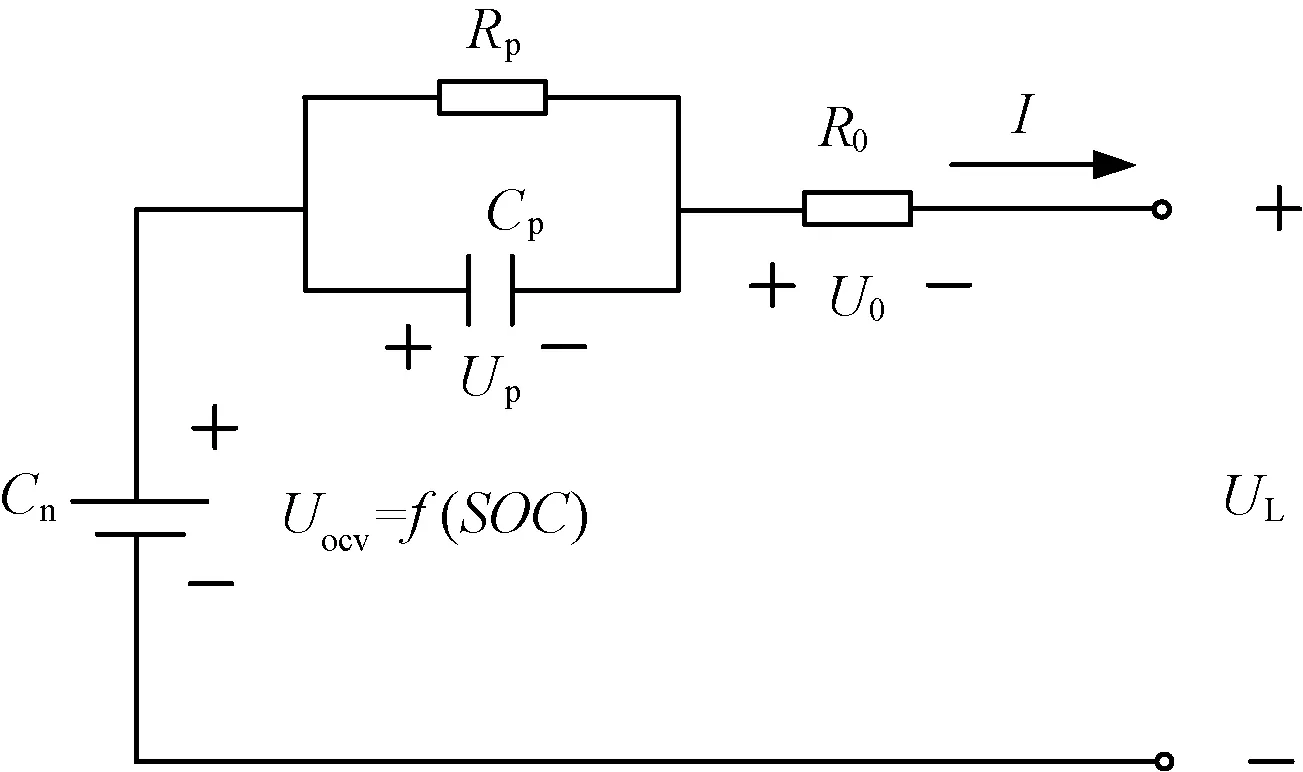
图1 锂离子电池一阶RC等效电路模型Fig.1 First-order RC equivalent circuit model of lithium-ion battery

图1中，Cn为电池的标称容量；Uocv为开路电压，反应电池的稳定状态，与SOC呈非线性函数关系；UL为锂电池负载端电压；I为电池充放电电流，放电方向为正；R0为欧姆内阻；Rp和Cp分别为极化电阻和极化电容，模拟电池因电化学极化和浓差极化产生的瞬态响应，均与SOC有关。

由等效电路关系得到电路方程，如式(1)～式(3)所示：

UL=Uocv-Up-IR0

(1)

(2)

(3)

式中，UL为端电压；Up为极化电压。

2.1 锂电池开路电压与SOC的关系

实验电池是某公司的磷酸铁锂电池，标称容量12Ah，标称电压3.2V。笔者认为以0.2C电流充电至3.65V为满电状态，SOC记为1，放电至2.5V为完全放电状态，SOC记为0。

通过对电池进行脉冲充放电，并且充分静置，可以得到不同SOC处的开路电压值，并根据开路电压变化特征，在SOC小于0.4阶段进行指数拟合，以0.7为分段点，对SOC大于0.4阶段进行分段线性拟合，得到Uocv-SOC关系如图2所示。

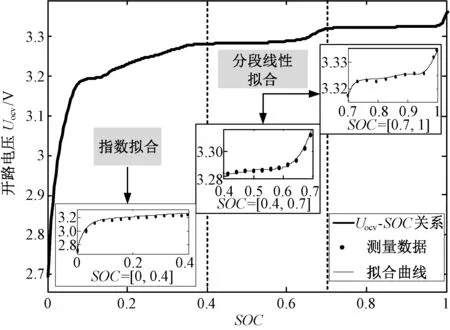
图2 所测磷酸铁锂电池开路电压与SOC关系曲线Fig.2 Measured open circuit voltage versus SOC curve of lithium iron phosphate battery

2.2 锂电池模型参数辨识

对电池时域方程进行s变换得到输出电压频域方程：

UL(s)=Uocv(s)-Up(s)-U0(s)

(4)

式中，s为拉普拉斯算子。

定义系统传递函数为：

(5)

根据脉冲响应不变法进行z变换得到：

(6)

式中，τ=RpCp。

即得到如下形式的传递函数：

(7)

差分方程为：

a0y(k)+a1y(k-1)=b0u(k)+b1u(k-1)

(8)

因此迭代求解a0，a1，b0，b1的过程就是辨识阻容参数R0，Rp，Cp，τ的过程，二者关系如式(9)所示：

，b1=-R0e-Ts/τ，

a0=1，a1=-e-Ts/τ

(9)

引入带外源输入的自回归滑动平均模型[22]如式(10)所示，有效减弱测量噪声对其辨识结果的影响。

(10)

式中，e(k)为白噪声；C(z)e(k)/A(z)为输出中的噪声部分。

系统辨识理论中，预报误差法[23]辨识范围广，抗噪声能力强。预报误差法原理如图3所示，根据k时刻之前的输入输出数据得到k时刻输出量的预报值，以该值和真实输出值间的误差作为准则进行参数辨识。通常参数辨识准则中的误差项是待估参数函数，当误差项体现白噪声性质时，可认为与误差项对应的待估参数就是真实参数。根据预报误差法原理，辨识结果应使模型具有较好的预报性能，即需要找到合适的A(z)，B(z)，C(z)，使目标函数JN(θ)取得极值。

(11)

式中，θ=[a0，a1，b0，b1，c0，c1]T，利用目标函数及其一阶、二阶导数矩阵，采用高斯-牛顿法迭代求取最优解。

图3 预报误差法框图Fig.3 Configuration of prediction error method

为充分激发电池的动态特性，保证单周期内电池荷电状态不变，工程上采用具有近似白噪声性质的逆M序列作为激励信号[24]，设计如下实验。

(1)按照ΔSOC=10%进行脉冲放电。

(2)在每个SOC点处施加幅值为8A，最大频率为1/75Hz的逆M序列电流，电流激励和电压响应曲线如图4所示。

图4 SOC为0.9时逆M序列测试电流与端电压波形图Fig.4 Current profile of inverse M-sequence test method and identification results when SOC is 0.9

利用采样得到的电压电流数据，通过对式(10)中的待估系数a0，a1，b0，b1进行迭代求解，得到收敛解后，结合式(9)计算得到不同SOC点处的阻容参数见表1。由图4(b)，图4(c)可以看出，在逆M序列激励下，模型端电压能较好的跟踪真实值，误差为0.04V左右，说明所提方法建立的电池模型准确且能够体现电池的动态特性。

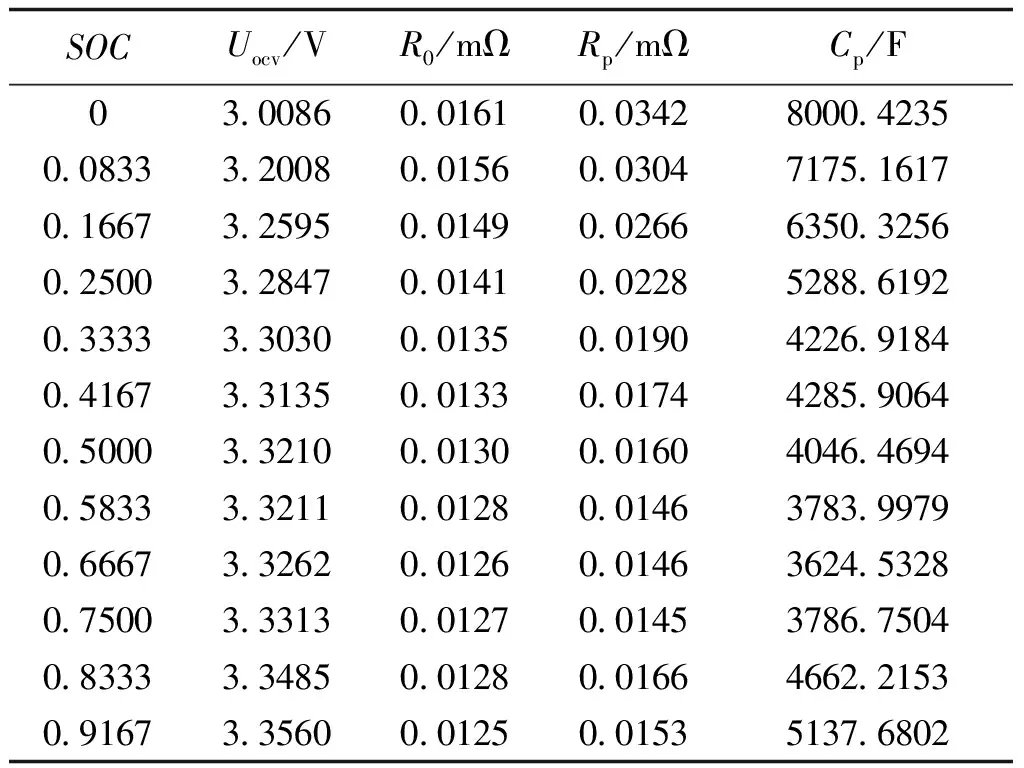
表1 所用磷酸铁锂电池模型参数辨识结果Tab.1 Parameter identification result of lithium iron phosphate battery

3 锂离子电池SOC估计

3.1 传统滑模观测器设计

由于电流采样频率较快，电流的微分可以忽略[17]，电池端电压的微分方程为：

(12)

将式(2)、式(3)代入式(12)得：

(13)

结合式(1)和式(13)得：

(14)

结合式(1)和式(3)得：

(15)

根据式(2)、式(14)、式(15)设计传统滑模观测器[25]：

(16)

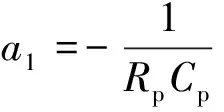
由于系统误差，电池状态方程为：

(17)

式中，ξ1，ξ2，ξ3为系统噪声且上界为d。取相应的K值满足李雅普诺夫稳定性函数：

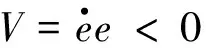
(18)

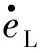
(19)

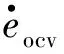
(20)

选择合适的开关增益并结合式(16)、式(19)、式(20)可获得较精确的SOC，并具有较强鲁棒性。

3.2 开关函数的影响

传统滑模观测器通常采用符号函数[16]，函数形式如式(21)所示：

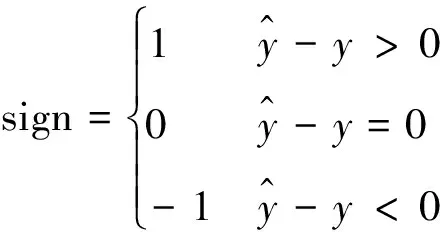
(21)

SOC估计过程中以预测电压和实际电压的差值作为反馈量，采用简单的开关函数，便可以得到电压和SOC的预测值。但是，开关函数的不连续性导致滑模观测器存在不可避免的抖振问题。削弱抖振问题可以采用低通滤波器，但同时会带来时间延迟和削弱幅值的问题，导致观测器估计精度下降。本文提出改进滑模观测器，以sigmoid函数作为开关函数，函数形式如式(22)所示：

(22)

sign函数和sigmoid函数的波形如图5所示。通过归一化处理，两种函数曲线均在±1之间。通过改变式(22)中自适应参数m的大小，控制sigmoid函数的斜率。

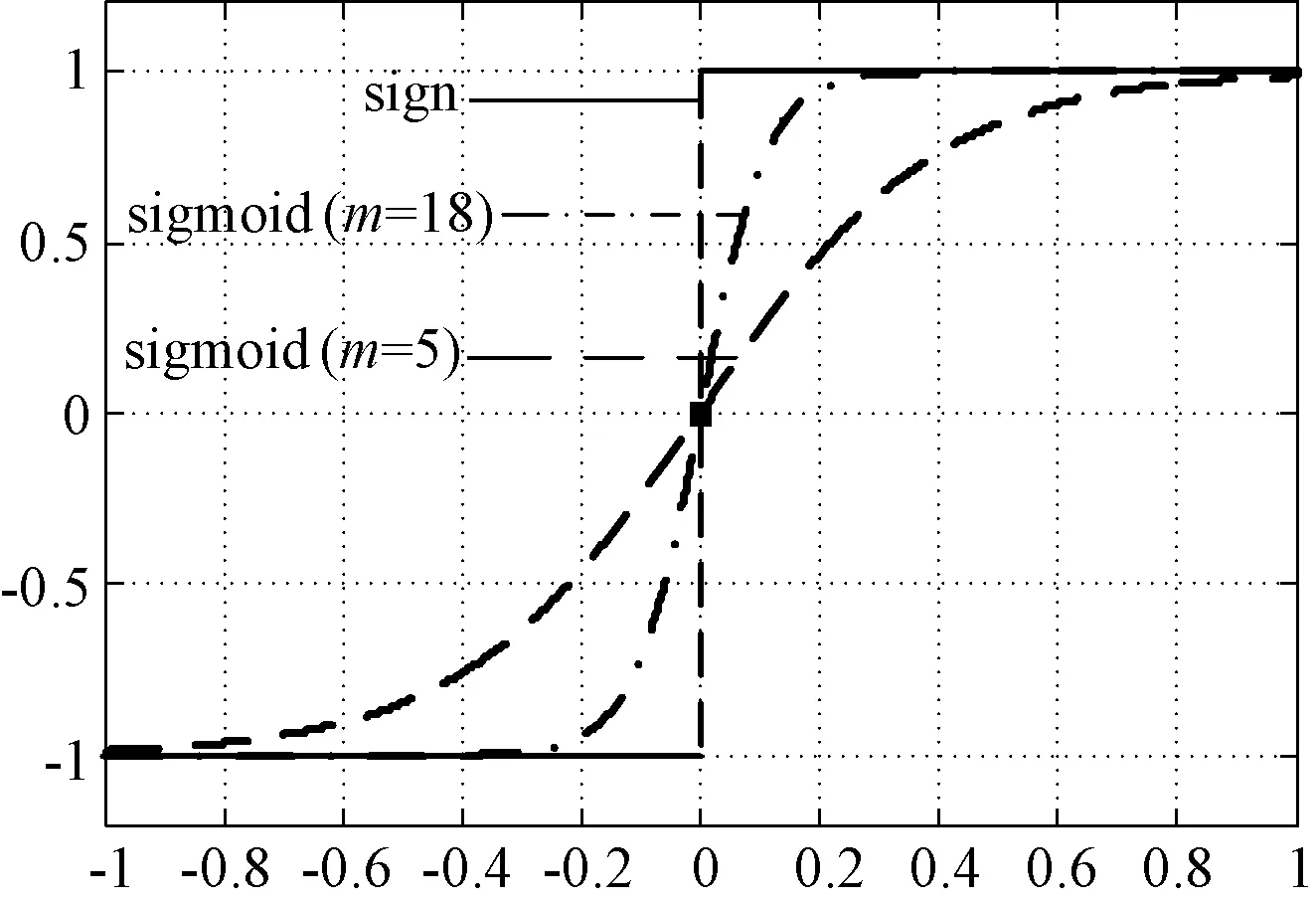
图5 不同开关函数的曲线Fig.5 Curves of different switch functions

由函数曲线可看出，当误差较大时，2种函数数值趋于相同；当误差较小时，与符号函数相比，sigmoid函数状态点缓慢到达切换面，从而起到削弱抖振的作用。此外，m取值不同，sigmoid函数波形有较大差别，作为开关函数会影响观测器的性能。m取值越大，抑制抖振的效果越差，m值越小，收敛速度越慢。因此需要根据实际系统结构，结合李雅普诺夫稳定性函数选择合适的m值，有效削弱估计量的抖动，本文m值为18。

本文提出的改进滑模观测器方法估计锂电池SOC的系统框图如图6所示，首先根据预报误差法得到的电池模型参数、电池输出电压和输入电流估算电池开路电压Uocv，然后根据开路电压和SOC的关系得到SOC估计值，进而由模型参数和SOC的函数关系更新下一步长的模型参数。

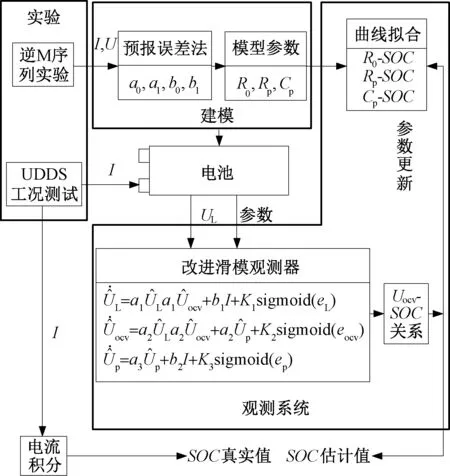
图6 基于改进滑模观测器的SOC估计系统框图Fig.6 Configuration of improved sliding mode observer proposed in present work for SOC estimation

4 实验对比分析

为了验证所提SOC估计方法的有效性，采用美国城市道路工况(UDDS)对电池进行测试，UDDS工况测试波形如图7所示。实验电池为某公司生产的12Ah磷酸铁锂电池，置于恒温箱内保证电池测试环境温度为恒温25℃，并与Chroma 17011电池测试系统连接。通过系统程序控制电池充放电，同时采集电池电压电流数据，采样频率为1Hz，整个测试平台如图8所示。

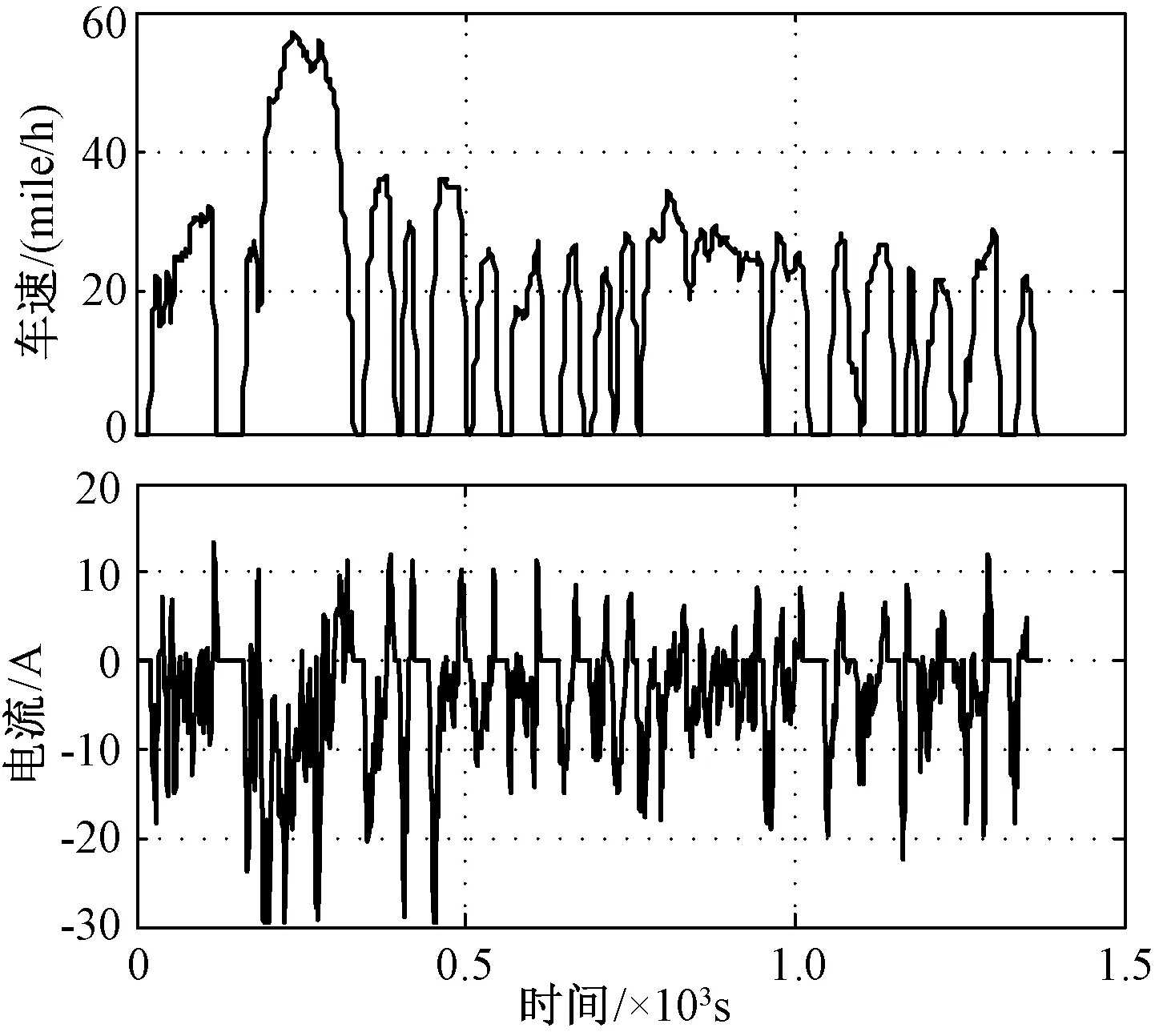
图7 UDDS工况测试波形Fig.7 Whole UDDS test profile

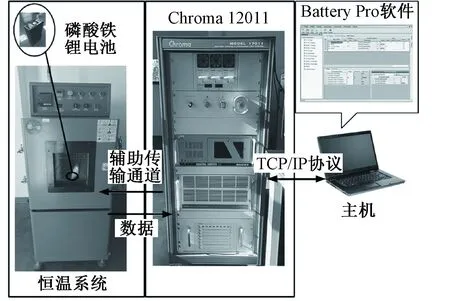
图8 电池测试平台示意图Fig.8 Schematic of battery test bench

采用预报误差法对模型参数进行离线辨识，并使用基于sigmoid函数的改进滑模观测器估计锂离子电池的SOC。电池端电压的估计结果如图9所示，电压误差为0.02V，证明采用本文建模方法，模型准确且能充分反映电池的动态特性，改进滑模观测器可以进一步消除参数变化带来的模型误差。

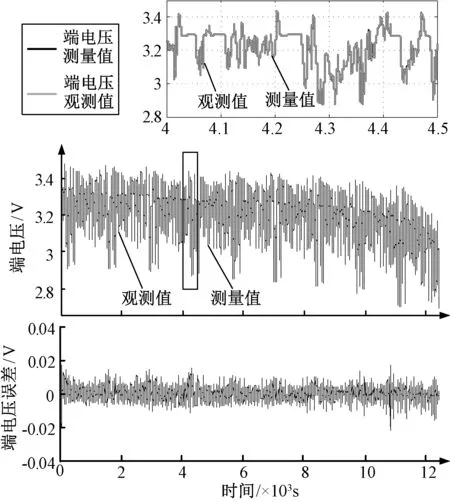
图9 端电压估计结果及误差曲线Fig.9 Estimation result of model voltage and error

通过给定不同的SOC初值，验证所提方法的鲁棒性。在UDDS工况下测试锂电池，SOC的真实值是在恒温25℃且初值为1的条件下由电流积分法计算得到。SOC初值与给定值相同的情况下，估计结果如图10，图11所示。结果表明，在滑模观测器的作用下，估计值很快收敛到滑模面，并在滑模面上下抖动，估计误差绝对值有增大的趋势，随后在开关函数的作用下收敛到滑模面。使用ISMO得到的SOC估计值在整个UDDS工况过程中收敛于SOC真实值，绝对误差稳定在3%范围内。与CSMO相比，ISMO抖振减小了50%，证明采用sigmoid函数的ISMO可以有效削弱估计SOC时出现的抖振现象，并且对于复杂工况有很强的鲁棒性。

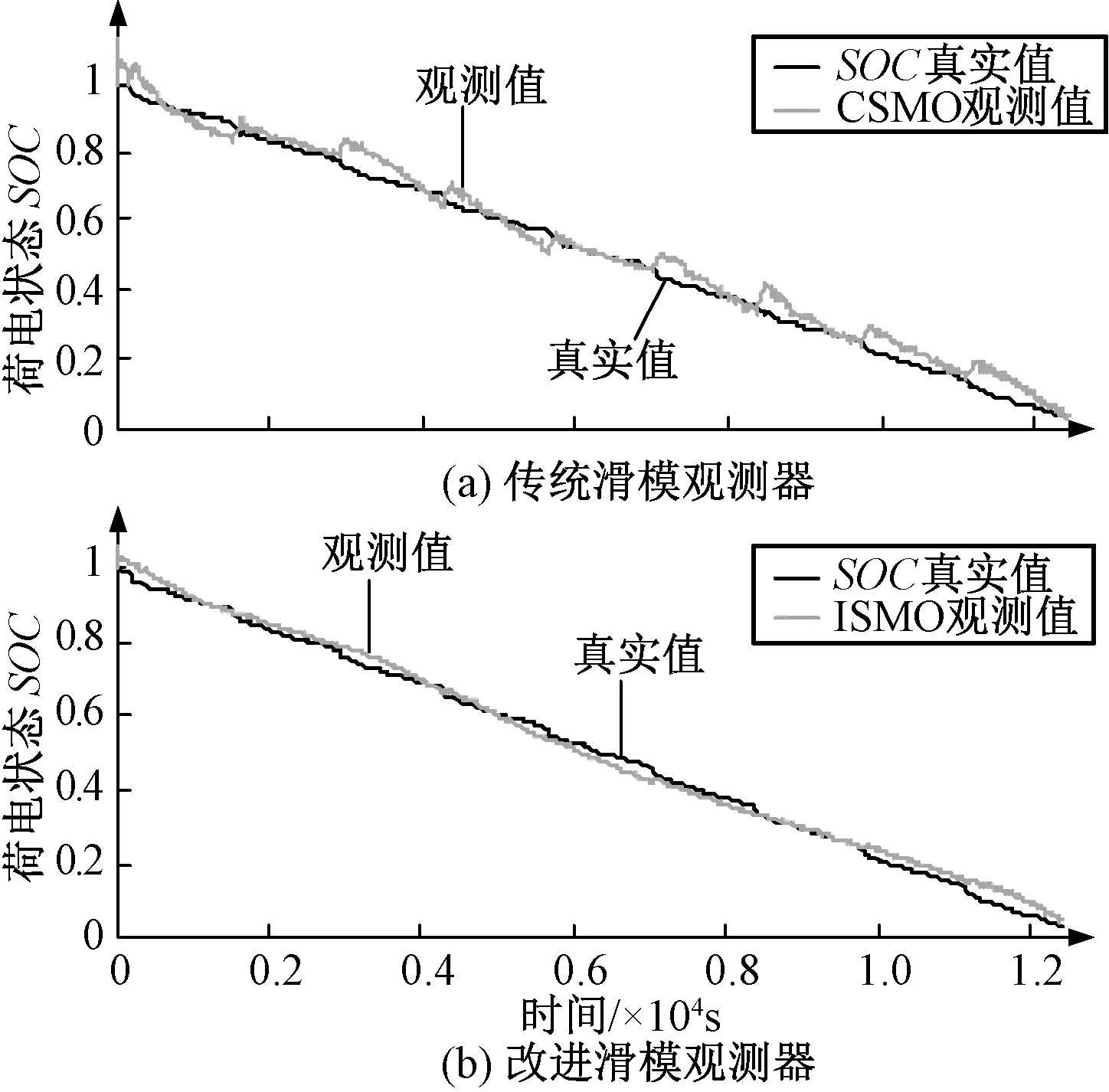
图10 真实初值和观测器初值均为1时SOC估计结果对比图Fig.10 Comparison of SOC estimation results when real initial SOC and observer’s initial SOC are all 1

图11 真实初值和观测器初值均为1时SOC估计误差对比图Fig.11 Comparison of SOC estimation error when real initial SOC and observer’s initial SOC are all 1

SOC初值未知的情况下，在SMO初值为0.8和0.7两种情况分别估计，结果如图12～图15所示。可以看出，在起始阶段，由于模型误差的存在，给定初值与真实值不同，会出现不同程度的偏差，但在起始偏差较大(30%)的情况下，SOC估计值仍可以快速上升并且能稳定的跟随SOC真实值。在开关函数的作用下，估计值在滑模面上下抖动。采用sigmoid函数后，抖动减小，SOC估计绝对误差稳定在3%范围内，收敛速度较快。

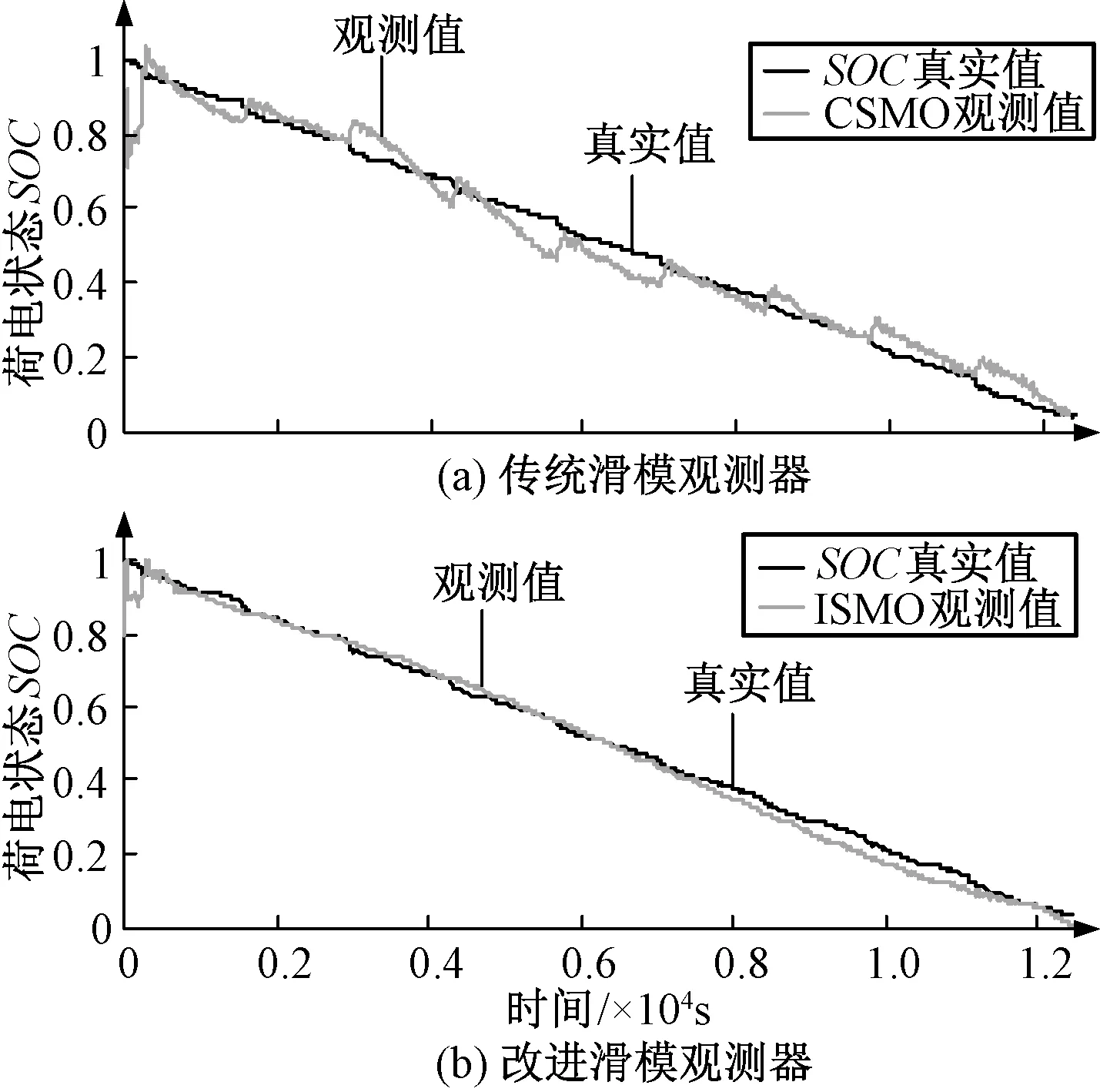
图12 真实初值为1，观测器初值为0.8时SOC估计结果对比图Fig.12 Comparison of SOC estimation results when real initial SOC is 1 but observer’s initial SOC is 0.8

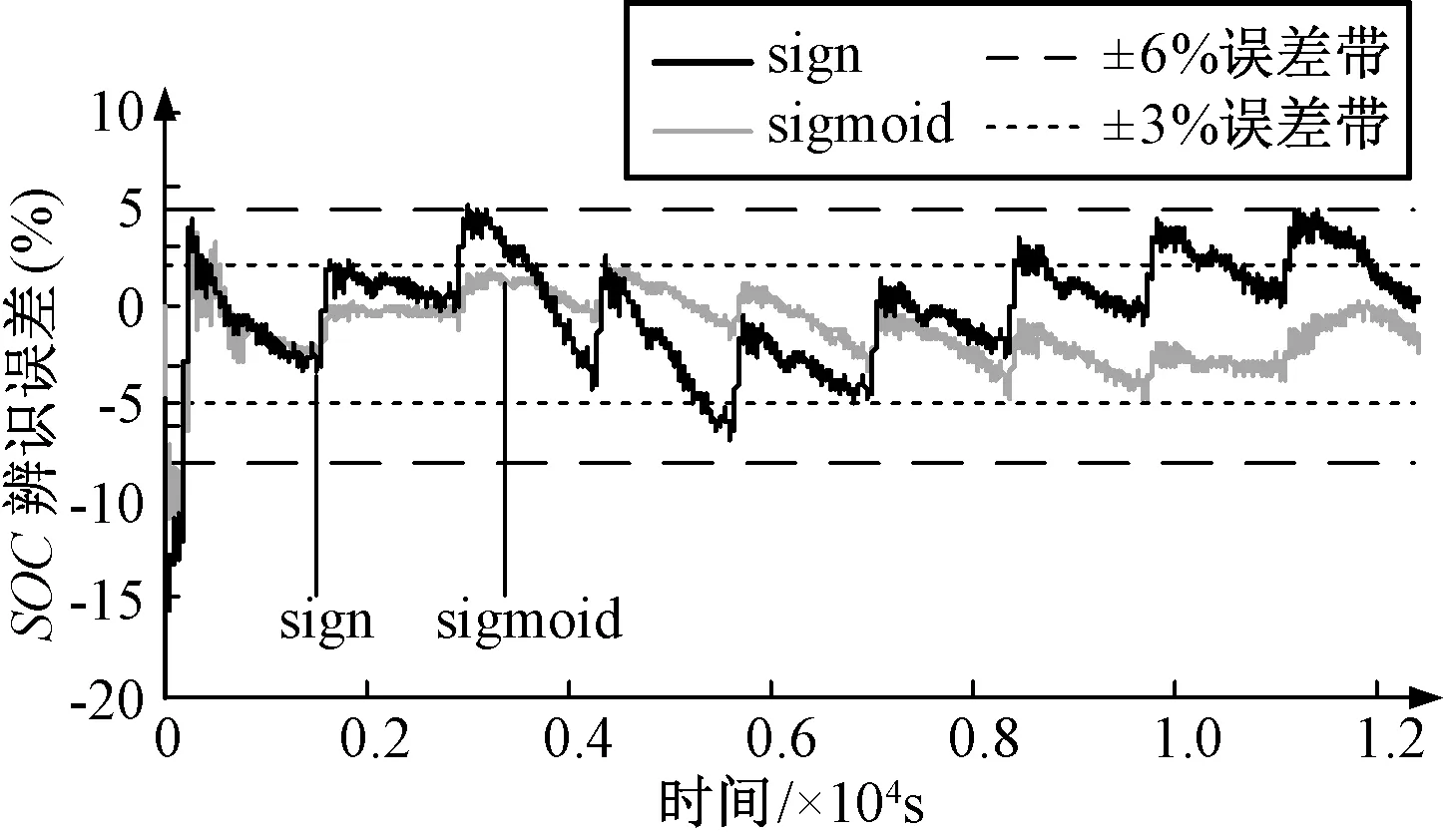
图13 真实初值为1，观测器初值为0.8时SOC估计误差对比图Fig.13 Comparison of SOC estimation error when real initial SOC is 1 but observer’s initial SOC is 0.8

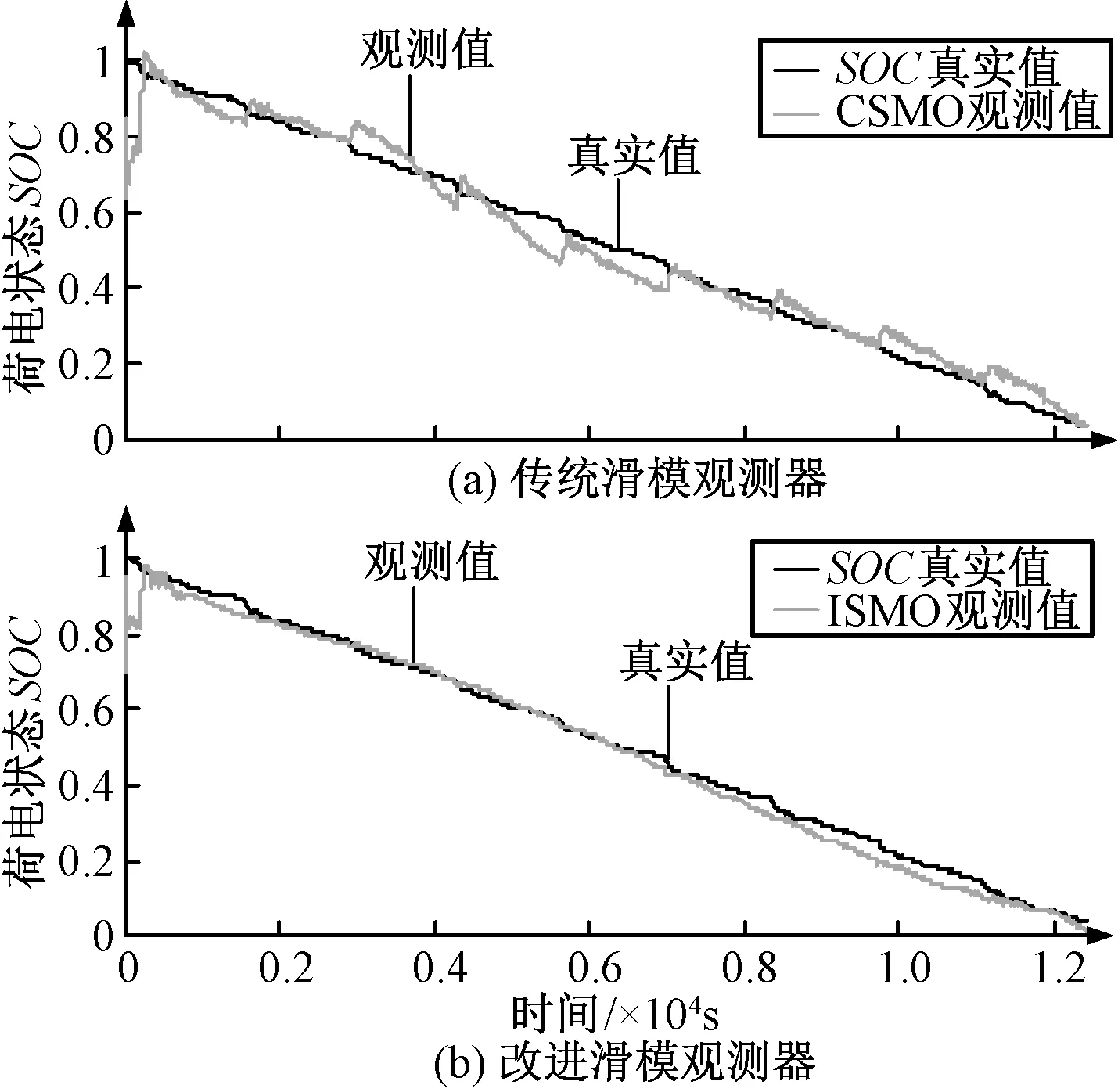
图14 真实初值为1，观测器初值为0.7时SOC估计结果对比图Fig.14 Comparison of SOC estimation results when real initial SOC is 1 but observer’s initial SOC is 0.7

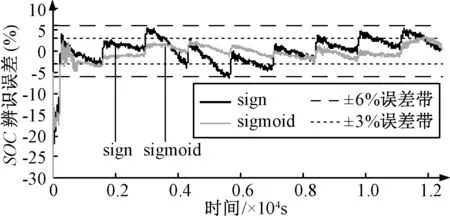
图15 真实初值为1，观测器初值为0.7时SOC估计误差对比图Fig.15 Comparison of SOC estimation error when real initial SOC is 1 but observer’s initial SOC is 0.7

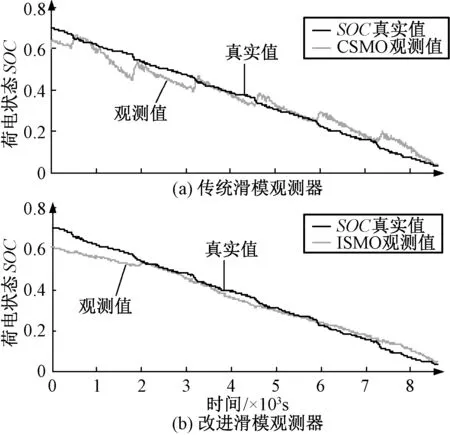
图16 真实初值为0.7，观测器初值为0.6时SOC估计结果对比图Fig.16 Comparison of SOC estimation results when real initial SOC is 0.7 but observer’s initial SOC is 0.6

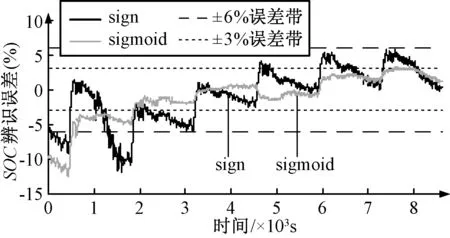
图17 真实初值为0.7，观测器初值为0.6时SOC估计误差对比图Fig.17 Comparison of SOC estimation error when real initial SOC is 0.7 but observer’s initial SOC is 0.6

由于电池在实际使用过程中往往不处于满电状态，为验证在不同SOC初值下的估计结果，将电池放电至SOC为0.7后采用UDDS工况进行放电测试，结果如图16，图17所示。可以看出，在电池初始SOC为0.7且给定值与真实值相差10%的情况下，ISMO能较好的跟踪SOC真实值，进一步证明改进滑模观测器的鲁棒性。

为了验证所提方法的适用性，设计循环混合工况实验进行验证，实验过程为：将SOC初值为0.2的电池以6A电流恒流充电，至SOC为0.5。再以UDDS工况电流放电至SOC为0.2，此混合工况循环6次，最后以6A电流恒流充电至SOC为0.5。为了验证所提方法的鲁棒性，滑模观测器初值设为0.1，验证结果如图18，图19所示。结果表明，初值不等的情况下，滑模观测器可以很快收敛到真实值，由于滑模观测器具有较强的鲁棒性，在恒流工况下的估计误差很小，绝对误差在1%范围内。恒流工况转为UDDS工况时以及UDDS工况转为恒流工况时，2个观测器均能快速收敛，但传统观测器出现较大的抖动，随着循环充放电次数的增多，传统观测器抖动稍有增大，2种观测器估计误差稍有增大，但估计误差均保持在±3%范围内，体现了所提方法的鲁棒性和长期准确性。

图18 混合充放电工况下SOC估计结果对比图Fig.18 Comparison of SOC estimation results under UDDS test mixed with constant current charging condition

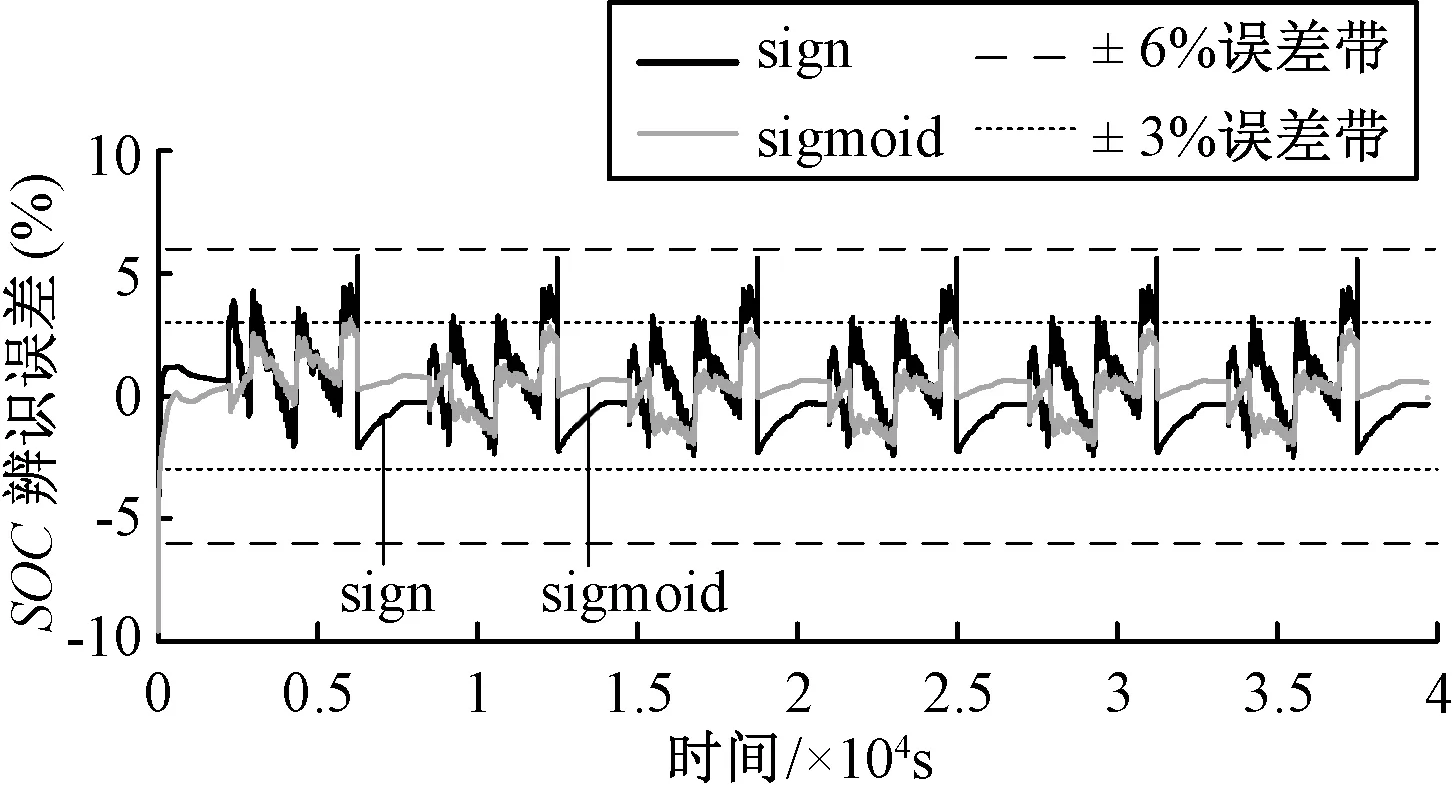
图19 混合充放电工况下SOC估计误差对比图Fig.19 Comparison of SOC estimation error under UDDS test mixed with constant current charging condition

实验结果表明，改进滑模观测器在SOC初值不确定甚至与实际偏差较大的情况下均能稳定收敛于真实值，并且对处于不同初始荷电状态下的电池估计效果均较好，适用于恒流工况以及复杂的道路工况。有效削弱了抖振，具有较强的鲁棒性和对状态量的跟踪能力。

5 结论

采用sigmoid函数作为滑模观测器的开关函数，代替传统滑模观测器中的符号函数，有效解决了传统滑模观测器进行SOC估计时存在的抖振问题，改进后的观测器抖振减小50%，估计误差大幅降低，为传统观测器估计误差的一半。采用预报误差法进行离线辨识，得到模型参数与SOC的关系，并根据SOC估计结果进行实时更新，提高了SOC的估计精度。分别在不同SOC初值以及初值未知的情况下进行UDDS工况和循环混合工况验证，改进滑模观测器结合预报误差法建模进行SOC估计，与传统滑模观测器的估计结果进行对比，所提方法可以有效削弱抖振，获得较精确的SOC，且具有较强的鲁棒性。

致谢：本文得到了北京交通大学张彩萍老师的指导，谨此致谢。