基于新型移相变压器的单电源配电环网潮流优化
2019-01-09田翠华游奕弘费雯丽
田翠华, 游奕弘, 费雯丽, 詹 隽
(武汉大学电气工程学院, 湖北 武汉 430072)
1 引言
配电网直接面向用户,是控制、保证用户供电质量的关键。但配电网网架结构薄弱,存在潮流分布不合理、功率绕送、线损率高等问题[1]。据统计,10kV及以下电网的损耗约占整个系统电能损耗的70%以上[2]。因此,配电网迫切需要有效的潮流控制手段来优化运行,降低网络损耗,减少供电成本,提高运行效率。
灵活交流输电系统(Flexible AC Transmission System,FACTS)通过改变线路参数,增强电网的潮流控制能力[3]。统一潮流控制器(Unified Power Flow Controller,UPFC)应用电力电子技术实现了潮流连续、快速的调节,但较高的装置损耗和昂贵的造价致使其不宜在配电网中大规模应用[4]。且UPFC过载能力有限,一旦所在线路发生故障,有可能损坏装置[5]。
基于有载调压开关的移相变压器(Phase Shifting Transformer,PST)在输电网中可以改善潮流分布不均,增强断面输送能力,降低系统短路电流,提高系统运行的可靠性与灵活性[6-8],具有更低的成本和更小的运行损耗。在响应速度要求不高的其情况下,可以起到与UPFC一样的补偿效果[9]。但尚未有研究涉及移相变压器在配电网中的应用。
ST (Sen Transformer)是K. K. SEN提出的一种三相四绕组的移相变压器[10]。文献[11]将ST改造成潮流控制器和降压变压器的结合体,文献[12]在ST的副边绕组增加中性点,但这些改进拓扑仍使用三相四绕组,制作难度高。文献[13]指出ST在降低网损的同时能解决潮流越限问题,提高系统安全,但没有进行降低网损的定量分析。
为了保证配电网优化运行的经济性,本文在这些工作的基础上,优化了ST的拓扑结构,提出了一种三相双绕组的新型PST,介绍了其电压调节特性,将其与ST进行了性能比较。分析了新型PST在配电环网中进行潮流控制的规律,推导了含新型PST的配电环网有功损耗优化及其实现条件,以这两点为基础提出了结合网络损耗旳潮流优化模型,对抽头算法进行了创新。在MATLAB/Simulink中对新型PST的潮流调节性能和潮流优化模型进行了验证。
2 PST的基本原理
2.1 PST拓扑结构
PST相当于一种串、并联混合型FACTS元件,结构如图1所示。PST是一个三相双绕组变压器,其原边绕组相当于自耦变压器,以星型接线的方式并联接入系统送端电压,构成励磁单元。原边绕组的自耦部分(绕组a1、b1、c1)和副边绕组 (a2、b2、c2)是PST的电压调节单元,均带有多个正负可调的中间抽头,两两串联向系统首端注入补偿电压。其中,绕组a1、c2串联构成A相的补偿电压,绕组b1、a2串联构成B相的补偿电压,绕组c1、b2串联构成C相的补偿电压。由于每相补偿电压取自两相电压的串联,通过调节抽头使这两相电压取正值、负值或零值,即可实现串联补偿电压的相位在0~2π的范围内变化。
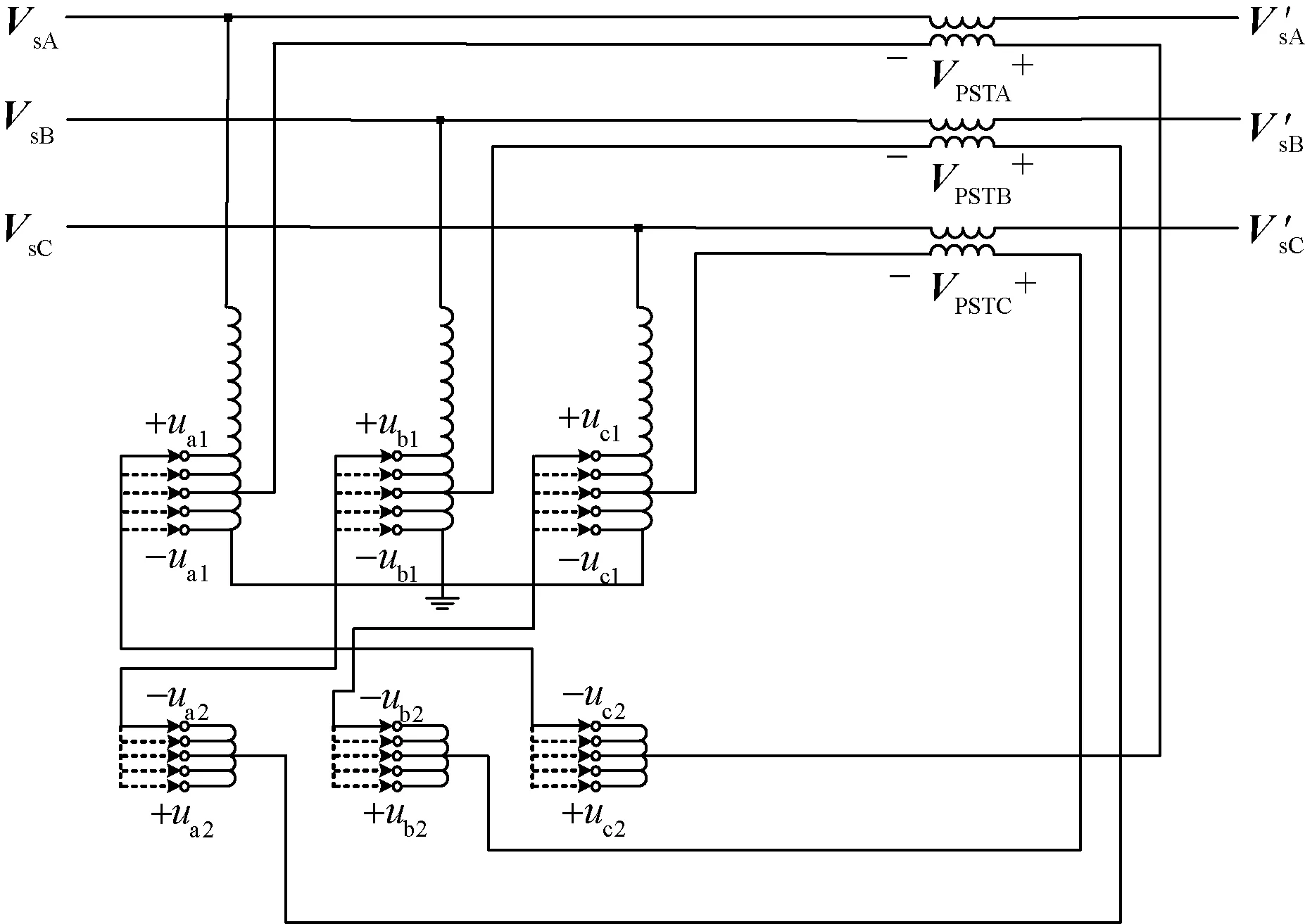
图1 新型移相变压器的拓扑结构Fig.1 Topology of novel phase shifting transformer
2.2 PST的电压调节特性
PST各调节单元的每级电压调节量相等,即ua1=ua2=ub1=ub2=uc1=uc2,抽头是可以多级正负调节的,设M为PST抽头的最大调节级数的绝对值,则各相串入系统中的电压表达式为:
(1)
式中,k为调节级数,ka1,ka2,kb1,kb2,kc1,kc2=0,±1,…,±M。
当M=1时,PST的电压调节单元可在(0,±1)级调节,以A相为例,PST的输出电压向量如图2(a)所示。首端A相电压向量的终点就是PST输出电压向量的起点,各坐标点为PST输出电压向量的终点。该电压向量叠加到首端电压上,就可以改变首端电压的幅值和相位。此时,PST可以输出9个电压向量(含零向量)。
当M=2时,PST的电压调节单元可在(0,±1,±2)级调节,即PST的拓扑结构如图1所示,其输出电压如图2(b)所示,其中β为PST输出电压与系统首端电压的相位差。此时,PST可以输出电压向量个数为25个(含零向量),例如要得到其中的电压向量V1,则绕组a1、c2的调节级数(ka1,kc2)为(2,-1)。
当M=3时,PST的电压调节单元可(0,±1,±2,±3)级调节,PST输出的电压向量如图2(c)所示,可以输出49个电压向量(含零向量)。

图2 PST的输出电压向量Fig.2 Output voltage vector of PST
以此类推,当PST在±M级的范围内调节时,PST可输出的电压向量数N=(2M+1)2。调节级数越大,PST可输出的电压向量分布就越密集,可控制的范围就越精确。
2.3 PST与ST的性能对比
表1为PST与ST输出电压向量个数随调节级数的变化情况。可以看出,在调节级数绝对值一样的情况下,PST可输出的电压向量比ST多,且随着可调级数增大,PST可输出的电压向量远远多于ST。

表1 ST和PST输出电压向量个数对比Tab.1 Comparison of number of output voltage vectors of ST and PST
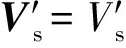

表2 ST和PST对等效首端电压的调节量对比Tab.2 Comparison of equivalent head voltage regulation by ST and PST
由表2可见,当绕组的最大调节量相等时,PST对幅值和相角的改变量远大于ST对幅值和相角的改变量。
ST和PST的性能对比如表3所示。可以看出,本文提出的PST比ST结构更简单,工程实现难度低;PST所需的二次绕组和有载调压开关数均少于ST,更具有经济性;在调节级数和最大调节量一样的情况下,PST可以输出更多的电压向量,其调压范围和移相范围更大,对潮流的调节范围也就更大。
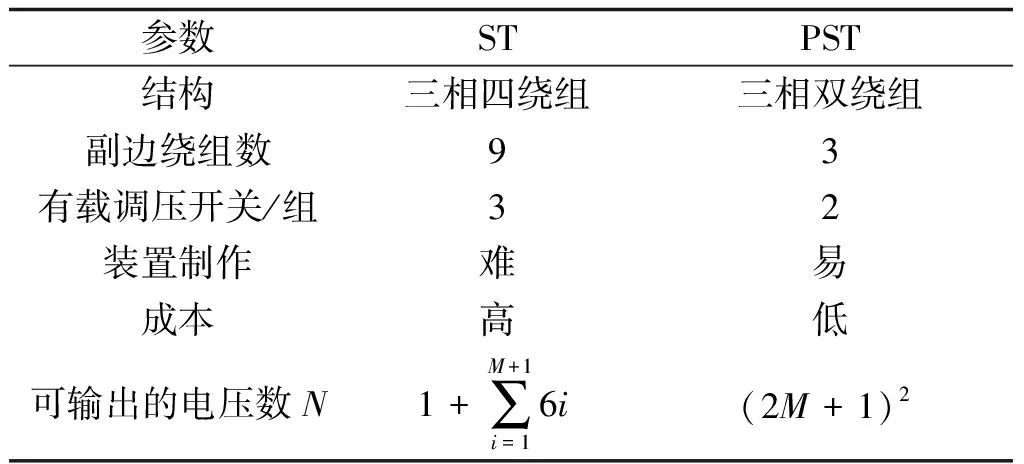
表3 ST和PST的性能比较Tab.3 Performance comparison between ST and PST
3 基于PST的配电环网潮流控制
比起拓扑简单固定的输电网,配电网结构复杂、负荷分支多、运行方式多变,其电阻成分较大(R/X>1/3),不能忽略。为简化分析,负载采用恒电流模型,将环网内所有负荷分支进行等值,其等效电路如图3所示。VA表示母线电压;IA1、IA2分别表示两条馈线的电流;VPST表示PST输出电压;Si表示第i条分支线路的等值负荷;SA1、SA2分别表示馈线1、馈线2的输出视在功率;Zm表示第m段环网线路的阻抗。
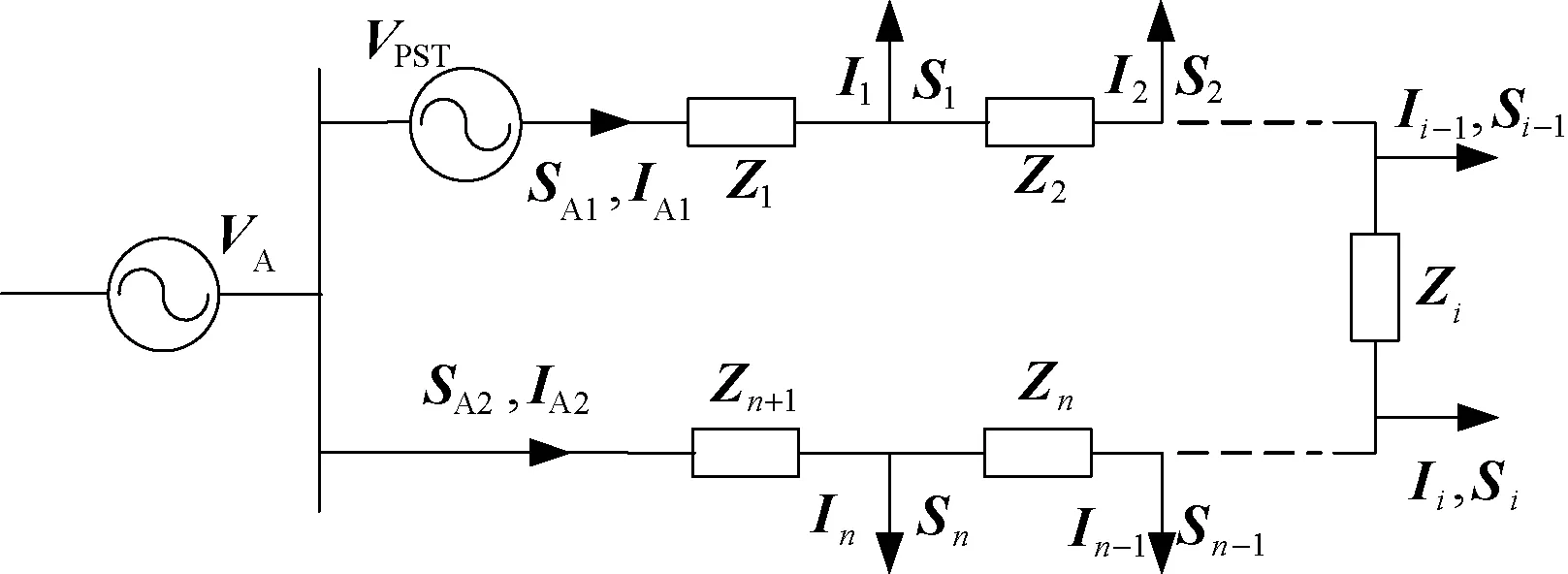
图3 配电环网的等效电路Fig.3 Equivalent circuit of distribution loop network
安装PST前,馈线1、2的输出视在功率为:
(2)
式中,ZΣ=RΣ+jXΣ,表示包括系统等值阻抗在内的环网总阻抗。
在母线首端安装PST后,PST输出电压VPST=VPST∠β,由于两条馈线首端电压不等,将在配电环网内产生循环电流Ic:
(3)
在母线电压恒定、忽略负荷静态特性的情况下,配电环网的循环功率Sc为:
(4)
当循环功率与线路功率同方向,线路功率改变量为正;反之,线路功率改变量为负。
由叠加原理可得:
(5)
(6)
整理得馈线1的潮流改变量为:
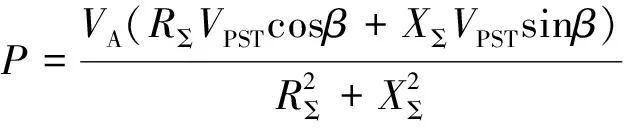
(7)
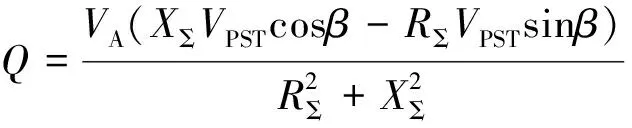
(8)
通过调节移相变压器的输出电压VPST∠β,即可控制配电环网中线路的传输潮流。这是因为,在馈线1首端加装一个移相变压器,相当于加入1个附加的辅助电压源,就可以产生1个循环电流,使得电流在环网中的分配更合理,也使得潮流在环网的分配更合理。
4 基于PST的配电环网潮流优化控制模型
为了同时实现潮流合理分布和网络有功损耗优化,本文提出了结合网络损耗旳潮流优化控制模型。
4.1 含PST的配电环网网络损耗优化
图4为简化的配电环网模型。每条线路的阻抗Zi=Ri+jωLi(i=1,2,3),线路L2和L3之间的联络开关闭合,分别连接恒电流负载IL1和IL2,此环网与其他系统之间的联系等效为一个电流源IL。

图4 配电环网简化模型Fig.4 Simplified model of distribution loop network
由叠加定理,该电路可等效为三个电路之和,如图5所示。则配电环网各线路的电流为:
(9)
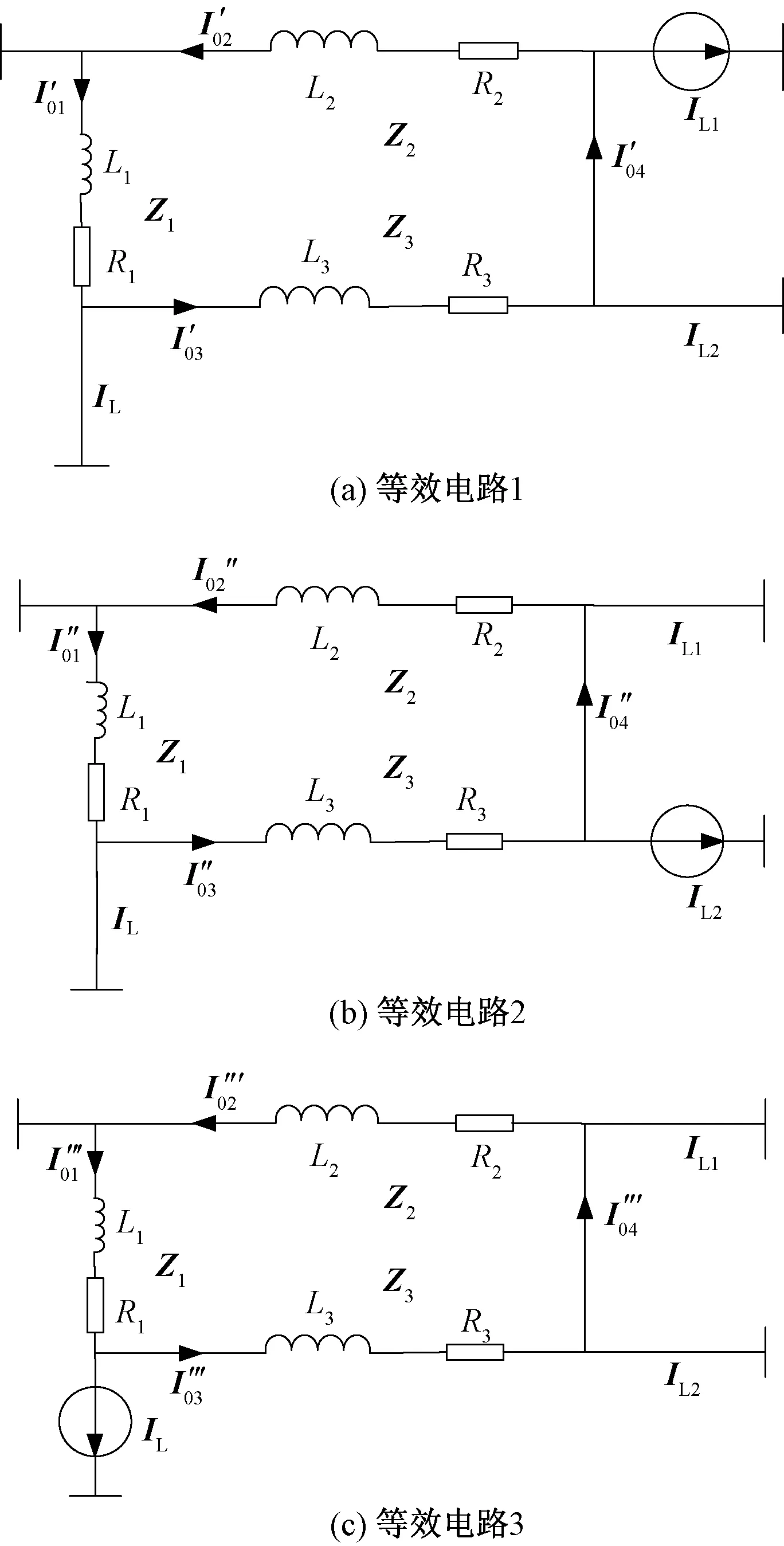
图5 叠加等效电路Fig.5 Superimposed equivalent circuit
可见,电流在环形网络中是与阻抗成反比分布。又由图5可得:
(10)
则环网线路损耗为:
(11)
由于IL1、IL2和IL均为恒定值,则当式(11)中Pi的第一项为零时,环网的线路损耗最小,此时流过各条支路的电流Imi为:
(12)
可见,当电流在环形网络中与电阻成反比分布时,有功功率损耗最小,最小值PLmin为:
(13)
由于各负载都是恒定不变的,则支路L1电流从I01变成Im1的改变量与其他支路的改变量相同,设此电流改变量为ILoop,则
(14)
当环网含有p条线路时,有:
(15)

由第2节的分析可知,PST将在环网中产生一个循环电流Ic,此时各支路的电流变为:
由叠加定理可得安装PST后环网的有功损耗优化为:
(16)
由式(16)可知,安装PST后的环网有功损耗优化值是在环网未安装PST时的有功损耗最小值的基础上,加入了由循环电流产生的有功损耗。
4.2 结合网络损耗的潮流优化模型
配电环网潮流优化控制的目标是在电网各节点电压不越限的条件下,通过调节控制变量,使配电网潮流分布合理,优化系统有功损耗,从而在保障电力系统安全稳定运行的同时,达到降低运行成本、提高经济效益的目的。
以有功网损优化为目标函数,以负荷节点电压为状态变量,以PST的输出电压为控制变量,对状态变量的约束条件采用罚函数的方式进行处理,数学模型如下:
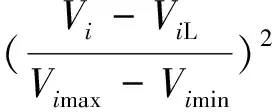
(17)
式中,PLoss为环网的有功损耗;λV为对节点电压越限的惩罚系数,其值可以根据经验及实验观察来确定;Vimax、Vimin分别为节点电压Vi的上下限;ViL为节点i的电压限值,定义如下:
配电环网潮流优化的等式约束条件为式(7)和式(8)。为了确保系统安全运行,将节点电压与母线输出的视在功率极限作为不等式约束条件:
(18)
控制变量约束条件为:
(19)
式中,SAmax为母线A的极限视在功率;VPSTmax、VPSTmin分别为新型移相变压器输出电压幅值VPST的上、下限。
4.3 PST的抽头选择算法
根据潮流优化模型计算出理想补偿电压值后,由于PST的离散调节,其最优投切点为最靠近理想值的点。传统的算法是分别计算出理想值与周围投切点的距离,再选择距离最近的点进行投切[14]。显然,这是很繁琐费时的。为了快速得到PST的最优投切点,本文提出了一个新算法。设PST的每级电压调节量为n(pu),理想值的标幺值为V0*=V0*∠β0,以A相为例进行说明。根据式(20)将V0*沿相坐标轴分解:
(20)
式中
利用向下取整的floor函数算出投切级数,从而求得离V0*最近的点,即最优投切点(ka1,kc2),如式(21)所示:
(21)
PST的控制流程图如图6所示。

图6 PST的控制流程图Fig.6 Control flow chart of PST
5 配电网潮流优化控制仿真
基于MATLAB/Simulink建立了配电环网的仿真模型,如图7所示。负载采用恒电流模型,各负荷分支Si对应的节点标号为i。
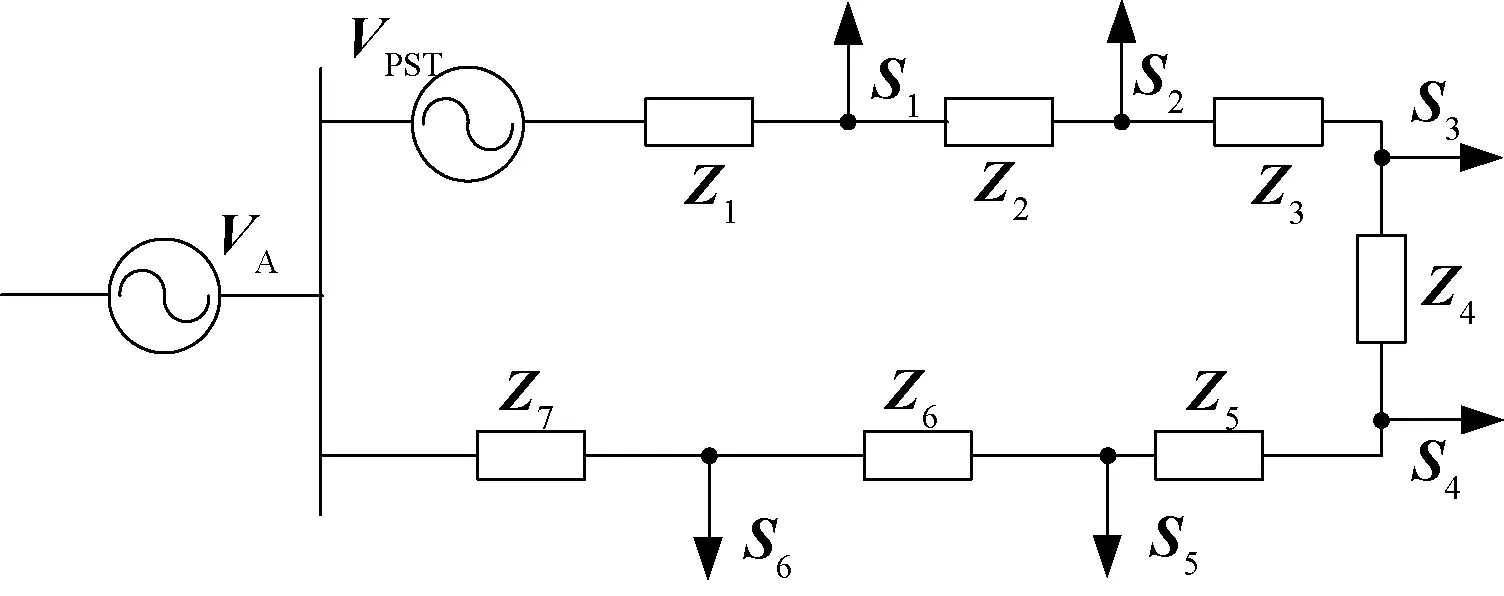
图7 仿真模型图Fig.7 Simulation model diagram
为了验证提出的装置及其控制模型的有效性,对三种运行状态进行了仿真:①t=0~1s,配电网闭环运行,尚未投入PST进行优化;②t=1~2s,投入PST仅均衡潮流;③t=2~3s,在含PST的配电环网中采用结合网络损耗旳潮流优化控制模型。
馈线出力的仿真图和柱状图如图8所示。未优化时,配电环网的两条馈线有功出力严重失衡,差值ΔP=2.09MW,不均衡度达42.6%;在配电环网中投入PST产生一个循环电流,使馈线1有功出力下降,馈线2有功出力增加,达到了均衡两条馈线出力的目的(ΔP=0.03MW);调节PST抽头同时优化损耗和潮流,此时两条馈线传输的潮流差值ΔP上升为0.27MW,但相较于未优化时,显著改善了两条馈线的有功出力,不均衡度为5.6%。
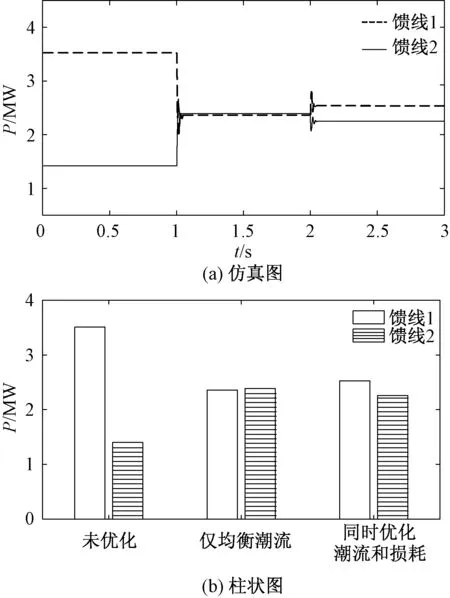
图8 馈线有功出力Fig.8 Feeder active power output
网络损耗随运行状态变化的情况如图9所示。未优化时,配电环网的潮流分布与阻抗成反比,网络损耗为0.382MW,网损率为7.78%;PST仅均衡馈线潮流时,网络损耗为0.342MW,网损率为7.20%;PST按照控制模型调节输出电压向量,同时优化潮流和损耗,使得配电环网的潮流分布与电阻成反比,网络损耗显著降低,其值为0.278MW,网损率为5.80%。
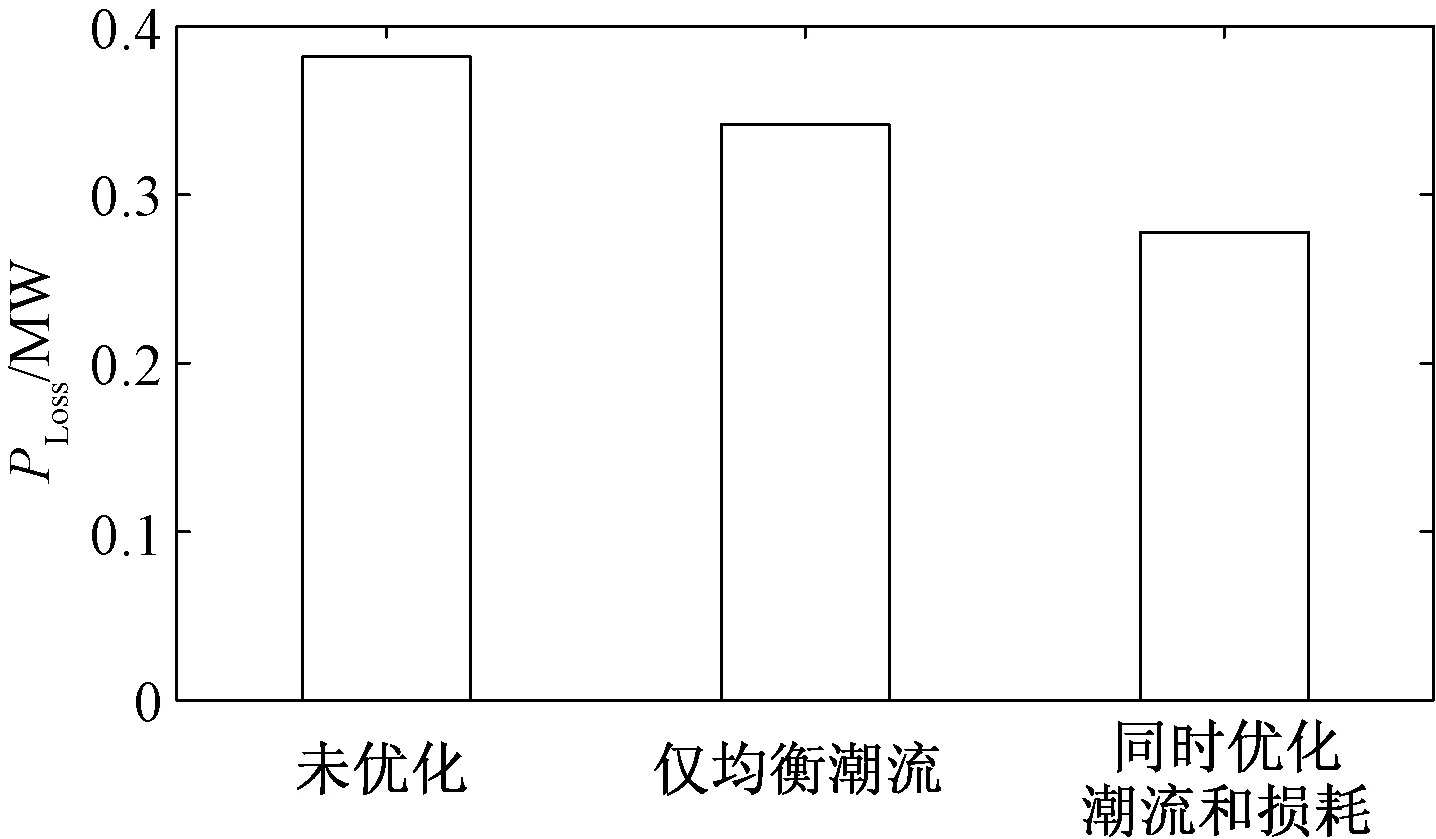
图9 网络有功损耗对比Fig.9 Comparison of active power loss in network
两条馈线有功出力和网络损耗随运行状态变化的情况如表4所示。可以看出,状态②完全均衡了线路潮流,但网络损耗没有得到明显改善;状态③中PST的控制模型不仅考虑了合理分配潮流,还考虑了网损优化,故馈线潮流没有完全均衡。在实际应用中,没有必要将分布不合理的潮流调节成完全均衡,且此种做法未大幅降低网络损耗,在经济性方面没有很大的优势。PST的控制模型以潮流不均衡度的稍稍上升来换取网络有功损耗的优化,在将潮流控制在合理范围内的同时,大大降低了网损费用,可以提高设备利用率和系统运行的经济性,实现投资效益的最大化。
节点电压变化情况如图10所示。未优化时,各节点电压普遍偏低,其中节点4的电压低于电压允许偏差范围的下限。当PST进行补偿后,状态②、状态③的各节点电压均变大,且未越限,电压偏差得到改善,说明PST提升了电压质量。
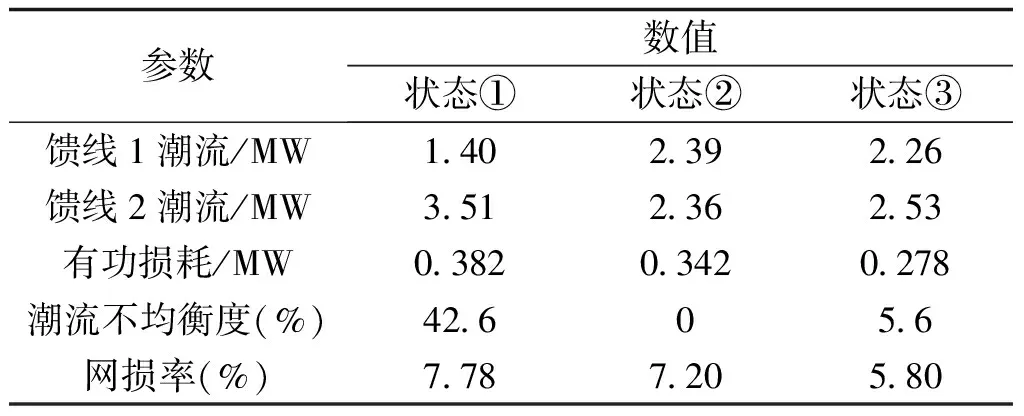
表4 不同运行状态下潮流与损耗的对比Tab.4 Comparison of power flow and loss in different operating conditions
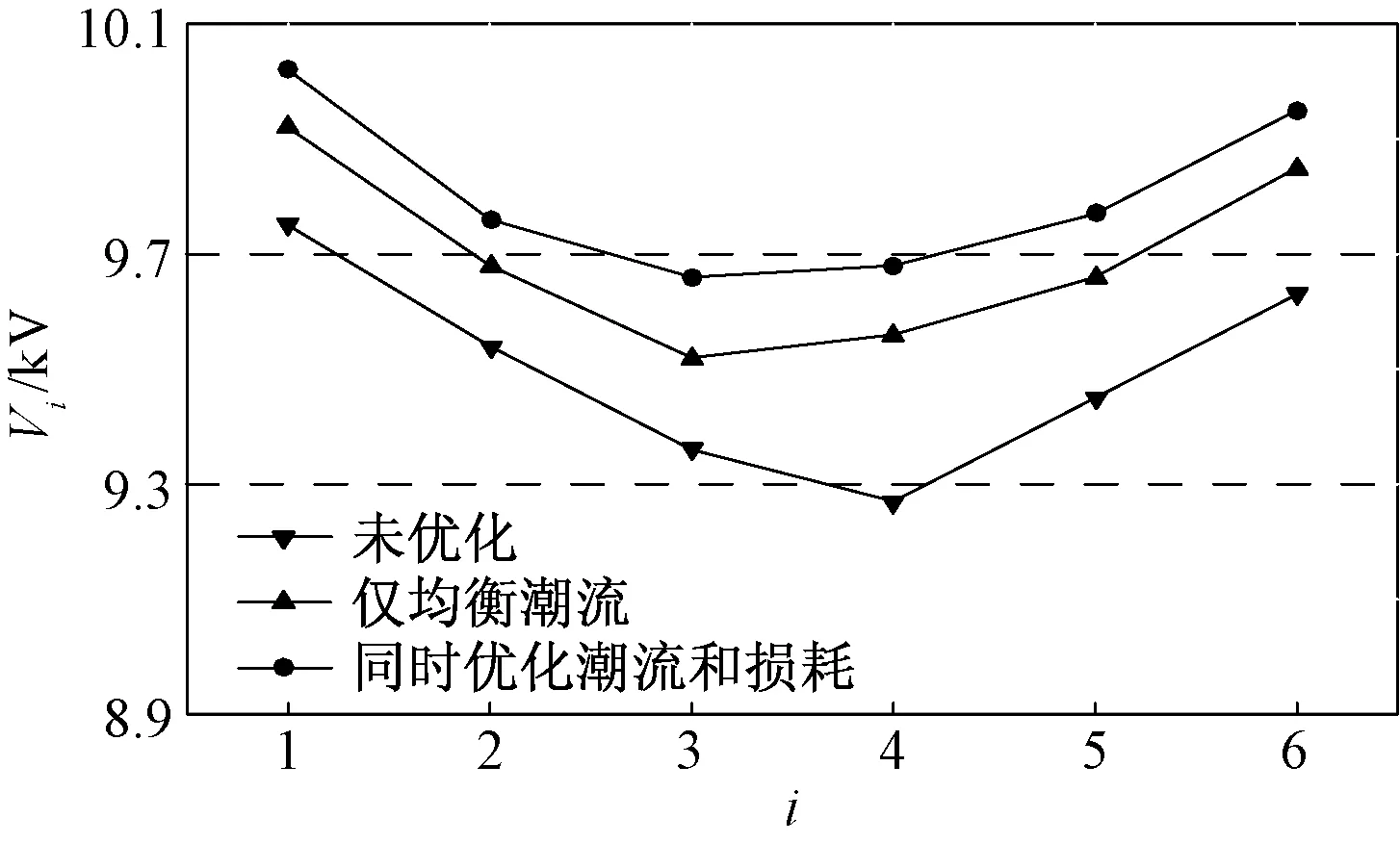
图10 不同运行状态下的节点电压Fig.10 Node voltage under different operating conditions
6 结论
(1)将PST的拓扑由四绕组优化成双绕组,提出了新型PST。相比ST,新型PST在使用更少的副边绕组和有载调压开关的同时,增加了调压、移相和潮流调节的范围。
(2)推导了PST对配电环网的潮流控制方程,通过调节PST输出电压VPST的幅值和相角,即可重新分配潮流。分析了计及PST时配电环网的有功损耗优化,提出了结合网络损耗旳潮流优化模型。
(3)PST通过产生一个循环电流来改变馈线出力,潮流调节性能优良。PST的潮流优化模型能在保证电网安全稳定运行的前提下,同时实现潮流的合理分布与有功损耗优化,网损率仅为5.8%,大大降低了运行成本。基于有载调压开关的PST能实现投资效益与运行经济性之间的均衡,应用前景广阔。
