2019年全国Ⅰ卷理科数学第16题的解法探究

摘 要：赏析2019年高考数学全国Ⅰ卷理科第16题的七种解法，探究思维能力在高考数学中的重要性.

关键词：高考题;赏析;思维能力

基金项目：甘肃省教育科学“十二五”规划2013年度“新课改理念下高三数学复习高效策略研究”课题（项目编号：GS[2013]GHB0771）.

作者简介：罗彩霞（1978-），女，甘肃民勤人，本科，中学一级教师，研究方向：高中数学教育教学.

高考数学试题特别强调能力立意，尤其是思维能力，因此我们应重视概念，回归教材，克服“轻概念、重训练”的现象，着力培养考生的思维能力，引导中学数学教学从“题型+技巧+训练”走向“概念+构建+思维”，逐步提高考生的思维能力.

2019年高考数学全国Ⅰ卷理科数学第16题，主要考查双曲线的几何性质、平面向量的线性运算、数量积等相关知识，考查考生的化归与转化能力、逻辑思维能力、运算求解能力及应用意识，考查的核心素养是逻辑推理、直观想象、数学建模、数学运算等，是一道区分度高，考查考生思维能力的一道好题.

1 试题呈现

题目 （2019年全国Ⅰ卷理科数学第16题）已知双曲线C∶x2a2-y2b2=1（a>0，b>0）的左、右焦点分别为F1，F2，过点F1的直线与C的两条渐近线分别交于A，B两点.若F1A=AB，F1B·F2B=0，则C的离心率为.

2 试题解析

分析 此题取材朴实，题干清晰，形式常见，但题中内涵丰富，字母较多，需考生冷静思考、琢磨，充分发挥观察力与想象力，为此先画草图，再结合求解离心率的通法：利用平面图形的几何等量关系以及圆锥曲线的定义、性质，想方设法找到关于a，b，c的一个等式，化简即可求解.

解法1 如图1所示，F1A=AB，F1B·F2B=0，所以OA⊥F1B.所以F1B：y=ab（x+c）.

联立y=ab（x+c），y=bax，解得Ba2cb2-a2，abcb2-a2.

则OB2=a4c2（b2-a2）2+a2b2c2（b2-a2）2=c2.

整理得，b2=3a2，即4a2=c2，c=2a.

所以e=ca=2.

解法2 因为F1B·F2B=0，所以F1B⊥F2B.

如图1所示，OB=OF1=c，所以∠BF1O=∠F1BO.所以∠BOF2=2∠BF1O.

因为F1A=AB，所以点A为线段F1B的中点.

又因为O为线段F1F2的中点，所以OA//F2B.

所以F1B⊥OA.

因为直线OA，OB为双曲线C的两条渐近线，所以tan∠BF1O=ab，tan∠BOF2=ba.

又因为tan∠BOF2=tan2∠BF1O，所以ba=2×ab1-ab2.

所以b2=3a2，即c2-a2=3a2，2a=c.

所以双曲线的离心率e=ca=2.

解法3 因为F1B·F2B=0，所以F1B⊥F2B.

如图1所示，由直角三角形性质知，OB=OF2，所以∠OBF2=∠OF2B.

又F1A=AB，所以A为线段F1B的中点.

又因为O为线段F1F2的中点，所以OA//F2B.

所以∠F1OA=∠OF2B.

又根据渐近线OA与OB的斜率互为相反数知，∠F1OA=∠BOF2，所以ΔOBF2为正三角形.

由F2（c，0）可得Bc2，3c2.

因为点B在渐近线y=bax上，所以3c2=ba·c2.

所以ba=3.

所以e=ca=1+b2a2=2.

解法4 双曲线C：x2a2-y2b2=1（a>0，b>0）的渐近线方程为y=±bax.

因为F1B·F2B=0，所以F1B⊥F2B.

所以点B在⊙O：x2+y2=c2上.

如图2，不妨设点B在第一象限，由y=bax，x2+y2=c2，a2+b2=c2，x>0，得点B（a，b）.

因为F1A=AB，所以点A为线段F1B的中点.

所以Aa-c2，b2，将其代入y=-bax得c=2a，故离心率e=ca=2.

解法5 双曲线C∶x2a2-y2b2=1（a>0，b>0）的渐近线方程为y=±bax，如图3所示，由F1A=AB知点A为线段F1B的中点.

又因为O为线段F1F2的中点，所以OA//F2B.

因为F1B·F2B=0，所以F1B⊥F2B.

所以OB=OF2.

所以∠OBF2=∠OF2B.

又因为OA//F2B，所以∠F1OA=∠OF2B.

因为∠BOF2=∠AOF1，所以∠BOF2=∠OF2B.

所以ΔOBF2为正三角形，可知ba=tan60°=3.

所以e=ca=1+b2a2=2.

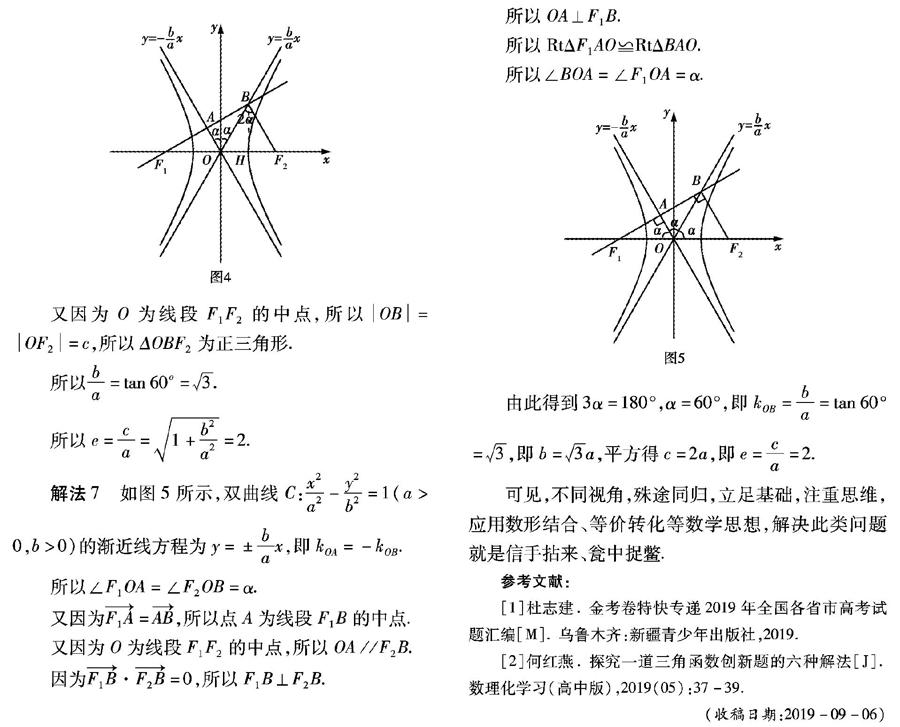
解法6 双曲线C：x2a2-y2b2=1（a>0，b>0）的渐近线方程为y=±bax，如图4所示，设∠AOy=α，则∠BOy=α.

因为F1A=AB，所以点A为线段F1B的中点.

又因为O为线段F1F2的中点，所以OA//F2B.

所以∠OBF2=2α.

过点B作BH⊥OF2，垂足为点H，则BH//y轴.

则有∠OBH=α，所以∠HBF2=α.

易得ΔOBH≌F2BH，所以OB=BF2.

因为F1B·F2B=0，所以F1B⊥F2B.

又因为O为线段F1F2的中点，所以OB=OF2=c，所以ΔOBF2为正三角形.

所以ba=tan60o=3.

所以e=ca=1+b2a2=2.

解法7 如图5所示，双曲线C：x2a2-y2b2=1（a>0，b>0）的渐近线方程为y=±bax，即kOA=-kOB.

所以∠F1OA=∠F2OB=α.

又因为F1A=AB，所以点A为线段F1B的中点.

又因为O为线段F1F2的中点，所以OA//F2B.

因为F1B·F2B=0，所以F1B⊥F2B.

所以OA⊥F1B.

所以RtΔF1AO≌RtΔBAO.

所以∠BOA=∠F1OA=α.

由此得到3α=180°，α=60°，即kOB=ba=tan60°=3，即b=3a，平方得c=2a，即e=ca=2.

可見，不同视角，殊途同归，立足基础，注重思维，应用数形结合、等价转化等数学思想，解决此类问题就是信手拈来、瓮中捉鳖.

参考文献：

[1]杜志建.金考卷特快专递2019年全国各省市高考试题汇编[M].乌鲁木齐：新疆青少年出版社，2019.

[2]何红燕.探究一道三角函数创新题的六种解法[J].数理化学习（高中版），2019（05）：37-39.

（收稿日期：2019-09-06）