典型大口径转管机枪热-固耦合效应研究

2019-01-05吴永海王永娟

弹道学报 2018年4期

徐宁，吴永海，王永娟，徐诚

(1.南京理工大学机械工程学院，江苏南京 210094；2.淮阴工学院机电工程实验教学中心，江苏淮阴 223003； 3.南京理工大学格莱特纳米科技研究所，江苏南京 210094)

转管机枪的射频高，在射击过程中，身管内膛受到高频、高温、高压及高速流动的火药气体热载荷作用，并被周期性地快速加热和冷却，使身管产生剧烈的温度变化和非定常热应力。同时，弹头挤进膛线时与膛面的剧烈摩擦也使身管内壁受到瞬时加热。身管受到的热载荷具有振幅大、持续时间短、平均温度高等特点[1-5]。这种反复的高频热作用使身管温升高，内膛尺寸发生变化，加剧了身管的磨损、烧蚀。烧蚀磨损机理的研究表明，在造成内膛破坏的众多因素中，热是一个起着主导、控制作用的因素[1，6-7]。同时，身管的发热还会引起其他一些不良现象，在不同程度上影响武器的使用性能[8-13]。

本文以某大口径转管机枪身管为对象，运用热-固耦合场理论，分析身管在高频循环动态热载荷和瞬态膛压载荷共同作用下的瞬态温度响应、瞬态应力响应及温度场、应力场的分布规律，为提高转管机枪身管寿命和优化设计提供理论依据。

1 某大口径转管机枪身管的有限元模型

1.1 某大口径转管机枪身管的有限元建模

转管机枪的身管在发射过程中受到高温、高压及高速流动的火药燃气及弹带的热、化学及机械的作用，工作状况不仅恶劣且极其复杂，为便于分析计算，在建立有限元计算模型时，作如下基本假设：①忽略弹丸在飞行过程中对身管的挤进力；②忽略身管重力的影响；③身管尾部受轴向约束；④忽略身管定位孔、螺纹等局部细节的影响[9，12-13]，3D模型见图1。

为全面研究不同身管模型对有限元计算结果的影响，本文建立了2D身管轴对称模型、3D单管模型和3D三管模型3种有限元模型，并沿身管轴线取3个典型截面进行分析。每根身管由镀铬层和钢本体构成，根据其结构和传热特点，建模时将作为双层管处理[8]。3种有限元模型均采用HyperMesh工具，其模型规模对比见表1。

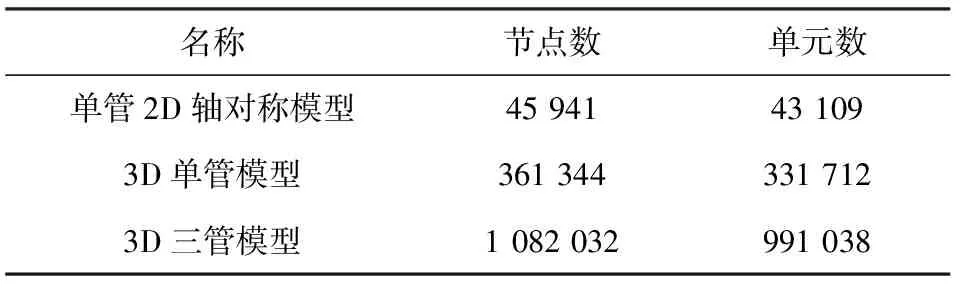
表1 身管有限元模型的规模对比

1.2 边界条件

本文将转管机枪的一个射击循环分为：弹丸膛内运动、出膛后的后效期及2发之间的间隔期共3个阶段。

①身管内壁边界条件。

弹丸发射过程中，火药气体是带热体的紊流沿身管轴向流动，呈现强烈的漩涡运动特点，因此身管壁与火药气体热交换主要形式为强迫对流换热，并伴随着较显著的辐射换热。但由于火药气体的压力、密度及吸收系数高，大部分的火药气体辐射能在到达内膛表面之前被吸收，与管壁的辐射传热量仅是对流传热量的1%。因此，本文假定火药气体与身管内壁间只存在强迫对流换热，辐射换热通过修正进行补偿。

内膛边界条件：r=r1。

(1)

式中：T(z，r1)为膛内流场温度；f(z，t)为内膛压力函数；g(z，t)为内膛表面温度函数；λ，G为Lame常数；u为径向变形量；r为身管半径，r1为身管内径；β为热应力系数；T0为环境温度；k为身管材料的导热系数；hinner为火药气体强迫对流系数。

②身管外壁边界条件。

身管转动时，空气横掠通过身管外壁，在身管外壁外表形成流动边界层，沿与身管轴线垂直的方向流动，身管外壁以强迫对流和辐射方式散热，其外壁边界条件为r=r2。

(2)

式中：r2为身管外径；houter为外壁气流对流系数[10-13]。初始条件为u(r，0)=0，T(r，0)=299。

在强迫对流条件下，当身管以一定的转速旋转时，可按Churchill-Bernstein准则计算强迫对流换热系数：

(3)

(4)

式中：λ为干空气的热导率，Nu为努塞尔数，Re为雷诺数，Re=ur2/ν，u为身管外壁速度，ν为空气的运动黏度(取16.48×10-6m2/s)；Pr为普朗特数(取0.7)。某大口径转管机枪的火药气体的强迫对流系数见图2所示。

2 3种身管模型计算结果对比分析

本文采用射击规范为：射频2 000 min-1，连射6发，停5 s，连射6发，停5 s，连射11发，停5 s，连射11发，共发射34发为一组，每组间隔4 min[14]。

图3、图4为3种身管模型A截面的计算结果对比。由图可以看出，3种模型计算结果的温度响应呈现相同的规律。在每组34发时，与2D轴对称模型相比，3D单管模型的温度峰值降低约1.4%，3D三管模型的温度峰值Tmax降低约4.45%；2D轴对称模型和3D单管模型计算得到的温度谷值Tmin非常接近。

图5为34发时3种模型温度分布曲线。由图5可以看出，3种模型的温度沿截面分布规律基本一致，其中2D轴对称模型和3D单管模型的计算值极为相近，而3D三管模型的计算值偏小，在一组(34发)结束时，内壁表面温度值小5.79%，这是由于热量在身管内的扩散所致。

3种模型的VonMises应力(σV)随时间变化规律基本一致，数值结果略有不同，见表2。表中,σV,max为峰值,σV,min为谷值。与2D轴对称模型相比，3D三管模型的内壁表面VonMises应力峰值约小4.76%。

从计算结果可知，使用3D三管身管模型的计算结果与2D轴对称身管模型和3D单管身管模型的计算结果比较，温度响应、温度分布和应力响应在规律上呈现相同的特点，但在数值上存在小于6%的差别。

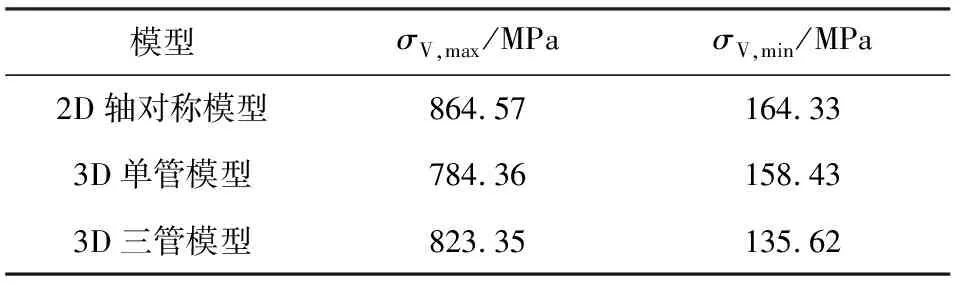
模型σV,max/MPaσV,min/MPa2D轴对称模型864.57164.333D单管模型784.36158.433D三管模型823.35135.62

3 某大口径转管机枪身管温度场分析

转管机枪在连续射击时，身管温度场始终处于非平衡状态，是周期性非稳态导热问题。根据传热学理论，非稳态导热分为2个阶段：初始阶段和正规状况阶段。当身管导热进入正规状况阶段后，其值仅与几何位置、边界条件有关，而与时间t无关。基于此特性，可以预测身管温度场，对于身管温度场的控制具有重要的意义。

正规状况阶段有2个特征：①身管上任一点的过余温度θ对时间的变化率(加热率或冷却率)是一常数，即身管进入正规状况阶段后，其3个截面的曲线斜率应相同。从图6(a)中可看出，经历2组射击后，身管并未进入正规状况阶段；②身管上任一点的相对温升系数为常数。射击时引起的外壁、内壁温升关系为

(5)

式中：Kθ为相对温升系数，θouter为外壁过余温度，θinner为内膛过余温度，Ta为环境温度。从图6(b)中可明显看出身管3个截面的相对温升系数都不是常数。这是由于转管机枪射频高，受身管材料热传导速率和散热限制，随着射弹数的增加，热量在身管内壁快速聚集，导致身管还未进入正规状况阶段，就已达到射击允许极限温度。

图7、图8为身管热状态分布图，第1组(34发)发射结束时，在A截面区域，管壁中的温度沿径向急剧衰减，内壁区域的温度最高，离内壁越远，温度越低。这是由于管壁较厚，内、外壁温差大(363.38 K)，管内温度梯度分布大，热流分布不均衡，最大热流出现在靠近内壁的薄层；而在C区域，由于管壁较薄，内、外壁温差仅为204.9 K，管内温度梯度小，但总体温度高，热流量大。之后的第2组、第3组发射，在A截面区域，管壁基础温度上升，内、外壁温差继续上升，温度梯度下降，热流量增加，最大热流量区域持续沿径向向外迁移。

在转管机枪发射时，3个截面6发弹，内壁温度响应呈现规则的周期性变化规律，其频率与射频相同，如图9所示。图中，d为距内壁距离。随着射弹数的增加，脉冲峰值温度呈现先迅速增加，随后逐步趋缓，脉冲振幅逐渐减小，但内壁表面残余温度大幅增加。沿径向向外，温度响应的振幅大幅衰减，剧烈改变区域集中于膛内表面薄层。在A截面上，第2发弹的内膛表面温度峰值增幅为56.04 K，至第6发弹时，峰值增幅仅为20.12 K。

图10、图11反映了在整个射击规范内3个截面铬层、外壁表面的温度响应。可以看出其响应规律一致，但C截面铬层表面峰值温度上升幅度较小，且与前1组相比，第2组、第3组的峰值分别上升0.52%和0.46%；C截面的外壁温度上升幅度较大，下降也较快，这是因为C截面的壁厚较小，强迫对流散热时热量迅速沿径向扩散，向周围环境散失的热量较多，外壁与内壁温度相差较小。

图12为B截面热流侵彻。102发、68发与34发射击结束时相比，内壁表面温度分别上升126.88 K、91.99 K，外壁表面温度上升37.71 K、99.44 K，这是因为B截面所在的身管壁面相对较薄，同时射击规范中有3次5 s的间隔，身管壁内的热量有充分的扩散时间，因此管壁内各点温度上升基本同步。根据牛顿对流换热公式，在外壁与周围环境强迫对流换热的情况下，热量散失到周围的空气中的总量增大。因此，从散热角度而言，身管管壁薄有利于散热。

为研究身管壁厚对散热影响，本文对不同壁厚的身管进行了对比分析,见图13，由于转管机枪射频高，壁厚较薄的枪管铬钢结合面上的最大应力较小。第6发弹时，在A截面铬钢结合面上，壁厚为7.75 mm的最大VonMises应力为924.6 MPa，而15.75 mm时的最大VonMises应力为1032.8 MPa。根据Manson-Coffin疲劳方程和Morrow方程预测身管寿命，当壁厚由11.75 mm减为7.75 mm时，寿命增加26.6%，如表3所示。表中，δ为身管壁厚，N为寿命。这是因为身管高转速产生强迫对流散热。身管壁厚越小，外壁温度越高，内、外壁的温差越小，热应力越小，释放的热量越多。

δ/mmN7.754 64111.753 40815.753 521

图14为内膛表面残余温度随射弹数变化，连续射击时，管壁越厚，内膛表面残余温度越低，内外壁的温差越大；截面热负荷越大，通过增加壁厚带来的内膛表面残余温度的降低幅度越大。因此，在承受热负荷大的截面，增加壁厚可以降低内膛表面温度。但是，当壁厚达到一定值时，再继续增加壁厚，带来的表面残余温度值降低极小。当截面厚度由11.75 mm增加到15.75 mm时，A截面内膛表面残余温度只降低了1.05 K，几乎可以忽略不计。这是因为管壁越厚，内外壁的温差越大，外壁温度越低，管壁存储的热量越多。根据牛顿对流换热公式，身管外壁温度越低，通过外壁向环境的散热量越小。另外，增加壁厚后，由于内膛表面残余温度降低，一次射击循环时管壁吸收的火药气体热量增多。当壁厚增加到一定值后，即增加的吸热量与损失的散热量达到一定的程度时，通过增加壁厚带来的内膛表面残余温度的降低极小，甚至有时增加了内膛表面残余温度。同时，增加壁厚带来了身管质量的大幅增加，对于武器的机动性极为不利。

4 转管机枪身管动态耦合应力分析

将热载荷和膛压载荷同时施加给膛内表面，进行耦合场计算，结果如图15～图17所示(图中压应力为正，拉应力为负)。

单发内膛Cr层内表面应力(A截面)如图15所示。从图15(a)中可以看到A截面内壁径向应力主要以膛压应力为主，热应力基本可以忽略，膛压应力曲线和耦合应力曲线几乎重合。图15(b)反映了内壁周向应力中，膛压载荷引起的应力为拉应力，而热应力为压应力，并且热应力的峰值大于膛压应力的峰值，因此耦合周向应力起始段有一个小的拉应力脉冲，但很快以热应力为主，由于此时膛压载荷引起的拉应力抵消作用，导致之后耦合周向应力的数值比热应力要小。从图15(c)中可以看到内壁轴向应力主要以热应力为主。图15(d)由于内膛表面受到火药气体冲击性载荷作用，其表面的耦合应力呈现陡峭的冲击性特性，但耦合应力峰值比相应的热应力峰值小。第1发弹发射时，在弹丸到达A截面瞬间，热载荷和膛压载荷同时作用，铬层表面耦合VonMises应力瞬时达到865.2 MPa。对比图中的应力峰值，可以看出在耦合应力的3个分量中，轴向分量对总耦合应力影响最大，径向分量对总耦合应力影响最小，而轴向分量和周向分量主要受热应力影响，因此热应力对总耦合应力的影响是主要的。

连续射击时，膛内铬层表面节点耦合VonMises应力成脉冲状，呈现剧烈上升、急速下降的规律，如图16(a)所示。由于膛压载荷的耦合作用，耦合应力的振幅比热应力小。但从绝对数值来说，仍然较大。在B截面，第1发弹的瞬时耦合VonMises应力达到943.7 MPa。随着射击的持续进行，脉冲振幅逐渐减小，第2发弹的振幅为907.7 MPa，到第6发弹时，脉冲的振幅降为829.6 MPa。与此同时，内膛表面残余耦合应力大幅增加。发射间隔期，内膛表面残余耦合应力值等于残余热应力值。由于内膛表面残余耦合应力的大幅增加，应力脉冲的峰值大幅增加，第6发弹时，脉冲的峰值达到1 264.4 MPa，但其作用时间非常短。应力脉冲在膛线起始部区域的值较大，其余区域应力峰值沿轴向逐渐降低。在C截面，VonMises应力脉冲的规律与B截面相同，但其峰值稍小，第1发弹瞬时VonMises应力峰值仅为883.8 MPa，同时其内膛表面残余耦合应力增加幅度稍小。

身管钢层表面的耦合VonMises应力脉冲规律如图16(b)所示。钢层表面的耦合应力脉冲峰值增加得较快，随着射弹数的增加，钢层表面与铬层表面的瞬时VonMises应力峰值的差距明显缩小。从第4发起，钢层表面的耦合应力峰值已超过了身管材料的静载极限应力，但危险应力的持续作用时间非常短，单发时不超过2 ms，由于材料的动载极限应力高于其静载极限应力，因此认为材料仍是安全的。图16(b)也说明了应力剧烈改变区域集中于膛内表面薄层，在身管内部，应力值持续在安全范围内。另外，无论B截面还是C截面，在每一发弹的内弹道期，都出现了非常明显的下行线。由于在钢层表面受膛压载荷与热载荷的共同作用，其耦合VonMises应力曲线是双峰曲线，但时间非常短，故在图16(b)中显示为一根线。随着射弹数的增加，热载荷的影响逐渐加大，残余热应力不断增加，热应力的峰值大幅度增加，从第2发弹开始，钢层表面的耦合VonMises应力主要由热载荷确定。

图17为连续射击时，铬钢结合面上的VonMises应力变化规律。从第2发开始，由于热载荷产生的应力峰值已经超过膛压载荷产生的应力峰值，居于主导地位。从第4发开始，由于残余热应力的存在，膛压载荷的主要作用是抑制热载荷产生的应力。热载荷引发的热应力规律与温度响应规律相似。内膛铬层表面热应力呈脉冲状，连续射击时，多个热脉冲作用使内膛表面残余热应力大幅增加，应力脉冲峰值逐渐增加，脉冲振幅逐渐减小。热应力沿身管轴向和径向分布不均匀，膛线起始部区域数值较大，膛口区域较小。沿径向向外，应力峰值迅速降低。