基于神经网络算法的弹丸阻力系数辨识

李金晟,常思江,陈升富

(1.北京航天长征飞行器研究所,北京 100076;2.南京理工大学 能源与动力工程学院,江苏 南京 210094)

气动参数对于常规弹箭的飞行稳定性及弹道轨迹具有重要影响。目前,弹箭的气动参数的估计方法已有许多,其中经典常用的有基于最小二乘准则的C-K法[1]、基于极大似然准则的输出误差法[2]以及结合了滤波思想的滤波误差法[3]。但是,这些方法在应用于实测飞行数据时,无一例外都会出现一些复杂的问题。其中较为普遍的一个难题便是对于真实系统缺少精确的数学模型。大多数传统的方法利用动力学模型来近似描述真实系统,这种近似会带来建模误差的问题。但对于建模误差的处理目前还没有成熟的理论可用,通常是将其简单的归为状态或测量噪声来处理,这种处理方式没有考虑到建模误差可能是确定性的而非随机性的[4]。为了解决上述传统方法存在的建模误差问题,相关人员开始采用人工神经网络(artificial neural networks,ANN)进行气动参数辨识,其完全基于对输入输出的测量而不考虑系统内部的物理机制。

基于神经网络的气动参数辨识方法主要有三类:一是基于动力学模型的辨识方法[5],其优点是无需预先计算基准气动数据,缺点是所辨识的气动模型仍是一个“黑箱”,无法得到具体表达式;二是基于稳定或控制导数的Delta法和Zeros法[6],其优点是可以辨识出气动模型,缺点是需预先得知较为准确的气动参数数据,从而利用其训练神经网络;三是将前馈神经网络(feed forward neural networks,FFNNs)与优化算法高斯-牛顿法(Gauss-Newton)相结合的神经网络-牛顿(neural Gauss-Newton,NGN)辨识方法[7],其独特之处在于无需预先对系统进行建模,不需求解运动方程。这三类方法已经成功应用于飞机、导弹、再入体等飞行器的气动参数辨识,但尚没有应用于弹丸。

本文针对某无控旋转弹丸的阻力系数辨识问题,采用基于误差反向传播(back propagation,BP)神经网络的NGN法进行研究,并对结果进行了分析。

1 BP网络辨识动力学模型

1.1 BP网络原理简介

BP神经网络是一种单向传播的多层前向网络,其分为输人层、隐含层和输出层。隐含层可以有若干层,每一层的神经元只接收前一层神经元的输出,同一层神经元之间不连接。该网络的拓扑结构如图1所示[8]。

1.2 辨识动力学模型

NGN算法区别于传统辨识算法的独特之处在于,利用神经网络强大的非线性逼近能力来减小建模误差。由于本文主要是辨识弹丸的零升阻力系数Cx0,且文献[2]已表明通过量测速度数据v便可实现对Cx0的辨识。故利用网络辨识出速度状态满足的关系式即可。

BP神经网络在对状态进行预测之前首先要对网络进行多次训练,使其具备联想记忆和逼近能力,具体的训练过程包括以下几个步骤[9]。

第1步:网络初始化。由质点弹道模型可得,加速度主要与速度、密度及零升阻力系数有关,而在标准条件下密度又是高度的函数。因此本文的输入向量为

X(t)=(vx(t)vy(t)vz(t)y(t)Cx0(t))

(1)

式中:t为离散的采样时间,Cx0(t)是通过对风洞吹风或理论计算所得的基准气动参数进行线性插值所得。基于X(t),输出向量为

Y(t+1)=(vx(t+1)vy(t+1)vz(t+1)y(t+1))

(2)

由输入、输出向量可得输入层节点n=5,输出层节点数m=4。

第2步:求隐含层输出H。由X(t),输入层和隐含层间连接权值wij及隐含层阈值a,求H。

(3)

式中:l为隐含层节点数;f(*)为隐含层激励函数,本文设置其为Sigmoid函数,表达式为

(4)

式中:β>0,本文取β=1。

第3步:求输出层输出Y(t+1)。由H,隐含层与输出层连接权值wjk及输出层阈值b,求预测输出Y(t+1)。

(5)

第4步:误差计算。由Y(t+1)和期望输出O(t+1),求出预测误差e及误差性能指标函数E。

(6)

第5步:权值与阈值更新。基于最速下降法,由e更新连接权值wij,wjk以及阈值a和b。

(7)

(8)

η(g)=ηmax-[g(ηmax-ηmin)/gmax]

(9)

式中:ηmax,ηmin分别为最大、最小学习速率;gmax为最大迭代次数;g为当前迭代次数。

第6步:判断算法迭代是否结束,若没有结束,返回第2步。为了提高迭代效率,本文设置了2个迭代终止准则,准则一为达到最大迭代次数gmax,准则二为误差性能函数E小于给定精度。

神经网络训练结束后,所得到的BP网络就可以看成一个非线性动力学模型,其表达了从n个输入自变量到m个输出因变量的函数映射关系。

2 NGN算法应用过程

当神经网络的相关参数调试恰当后,就可以对t时刻的任意测量输入变量X(t)进行预测,得到t+1时刻的输出变量Y(t+1)。接下来便可根据神经网络模型辨识所需的气动参数。

2.1 分段辨识思想

本文基于分段辨识思想提取阻力系数,即将雷达所测的速度数据划分为若干个小区间,在每一个小区间内由于速度变化很小,故可把该区间内的Cx0视为常数。

2.2 辨识准则

本文采用极大似然准则做为目标准则函数。在实际应用中由于弹丸自由飞行试验要求较为严格,这时系统的过程噪声很小,故目标函数可表示为

(10)

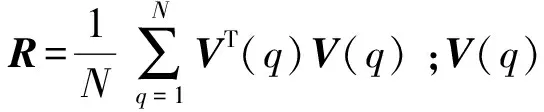
V(q)=ym(q)-y(q)

(11)

式中:ym(q)=(vm,x(q)vm,y(q)vm,z(q))T为已经过坐标转换的雷达量测速度数据;y(q)=(vx(q)vy(q)vz(q))T是基于当前输入,通过BP神经网络所计算的理论速度值。

2.3 灵敏度参数计算

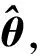
θ(r+1)=θ(r)+Δθ(r)

(12)

传统极大似然法是采用数值积分法联立求解弹道微分方程组与灵敏度方程组,从而获得灵敏度系数值。由于需要建立灵敏度方程组,故其较为繁琐,尤其是当模型比较复杂时,计算量会急剧增大。而NGN凭借其独特优势,极大地简化了计算灵敏度系数的过程,其方式如下:

(13)

式中:d为辨识系数个数;对于本文而言d=1;Ypk(t+1)为扰动输出,即给当前输入θd加一任意小扰动Δθd,利用已训练好的神经网络计算得到的输出值。

至此,利用式(13)计算的灵敏度值可求出修正量ΔCx0。重复以上的计算过程,每迭代一次都需要由似然准则函数计算Qr,直到当|1-Qr/Qr-1|≤0.01时,迭代收敛,计算结束。此时输出的Cx0就是该弹道段内辨识计算所得到的阻力参数。

3 数值结果分析

3.1 仿真验证

为了检验NGN算法的可行性,本文针对无控旋转稳定弹对其进行仿真分析,相关参数设计如下。①训练神经网络所需数据是由质点弹道模型计算所得,初始弹道诸元设置为:初速v0=1 100 m/s,射角θa0=45°,射向角ψ20=0,积分步长Δt=0.01 s;②BP神经网络调整参数:隐层层数为1,隐层节点数为l=10,学习速率ηmax=0.7,ηmin=0.4,动量因子α=0.1,权值wij、wjk和阈值a、b在[-1,1]间随机初始化,迭代终止准则一为最大迭代次数gmax=1 000,准则二为误差性能函数E≤0.001。

基于上述参数的设计,首先分析BP神经网络对动力学模型的逼近精度。本文基于质点弹道模型共生成7 713组弹道数据,随机选择其中5 000组数据来训练神经网络,利用其余的数据来测试神经网络的逼近能力。质点弹道的速度规律如图2所示。

本文采用均方误差(mean square error,MSE)及均方根误差(root mean square error,RMSE)来反映神经网络的预测精度,表达式为

(14)

BP神经网络的MSE及RMSE值如表1所示。

表1 神经网络模型的MSE及RMSE值

由表1可得,本文所建立的神经网络模型预测的3个速度分量值、高度值与真实值基本一致,且RMSE值相比于状态值而言非常小,这表明辨识效果较好。此外,神经网络的性能,即预测能力及收敛速度,则取决于网络的调整参数。经过调试分析可知,隐层层数、隐层节点数、最大迭代次数主要决定了BP神经网络的预测精度,而初始权值及阀值、学习速率和动量因子主要影响BP神经网络的收敛速度。

网络训练成功后,便可采用NGN法提取零升阻力系数。本文选择7 500组仿真雷达测速数据(其是由质点弹道模型与高斯白噪声叠加而成)。为了满足每一弹道段内阻力系数可以近似为常数这一条件,本文共设置500个弹道段,每个弹道段内最大速度降约为20 m/s。选定雷达量测噪声为σvx=σvy=σvz=0,辨识结果如图3所示。图中,Cd为阻力系数,Ma为马赫数。

由图2可得,基于NGN法辨识的阻力系数与基准阻力系数基本一致,辨识精度较高,可满足要求。相对而言,在跨声速段的辨识误差较大,这是分段小区间常数法的固有缺陷。经过调试可知,神经网络的预测精度决定了NGN算法的辨识精度,而灵敏度参数的设置决定了NGN算法的收敛速度。

3.2 实测数据处理

接下来分析NGN法对雷达实测飞行数据的辨识效果。本文所用雷达的测量误差:σγ=5 m,σβ=0.001 rad,σε=0.001 rad,σv=2 m/s。首先直接采用雷达量测数据训练BP神经网络,训练并调试成功后,其MSE及RMSE值如表2所示。

表2 神经网络模型的MSE及RMSE值

将表1与表2进行对比可得,BP网络基于实测数据的预测精度较低,其原因可能如下:一是神经网络参数设置仍不是最优;二是由于训练数据是雷达实测数据,结合六自由度刚体弹道模型可得,此时的状态量还受到其他参量的影响,如速度状态还受到攻角、弹道倾角、升力系数导数等的影响,而这些参量由于传感器的原因,并没有被作为输入输出量进行考虑;三是训练网络使用的基准阻力系数并不是该发试验弹丸最精确的系数。

NGN法辨识的零升阻力系数Cx0与马赫数Ma的关系如图4所示。

由图4可得,NGN法辨识的阻力系数与基准阻力系数在马赫数为[2,2.8]之间时,曲线基本一致,偏差较小;在马赫数为[1.2,2]之间时,辨识曲线已难以跟随基准曲线,误差较大;在马赫数为[1,1.2]之间时,辨识曲线围绕基准曲线振荡不断。出现上述现象的原因可能是:一是神经网络辨识的模型精度不高,这一点已在前文进行了分析;二是分段小区间常数法的固有缺陷使然;三是雷达量测数据存在野值,可考虑针对滤波数据进行训练和辨识。

为了进一步分析NGN法的应用特点,本文又采用目前工程应用已成熟的扩展卡尔曼滤波(extended Kalman filter,EKF)方法处理该发弹丸的实测数据,将分段辨识所得的阻力符合系数与对应弹道段内的基准系数相乘,便得到全弹道的阻力系数图,如图5所示。

由图5可得,EKF前期辨识精度较差,其原因是EKF法需要一定的数据量才能收敛于稳定值。

综上所述,在实际应用中可将NGN和EKF这2种方法进行结合,取长补短,从而达到工程要求。基于上述思想,本文在马赫数为[2.2,2.8]时,采用NGN法辨识的阻力系数;在马赫数为[1,2.2]时,采用EKF辨识的结果。然后对雷达测量弹道、基于理论基准阻力系数计算的弹道、基于辨识阻力系数计算的弹道三者的速度进行比较,如图6所示。

理论参数计算弹道、辨识参数计算弹道与雷达测量弹道的速度及位置的偏差均值如表3所示。

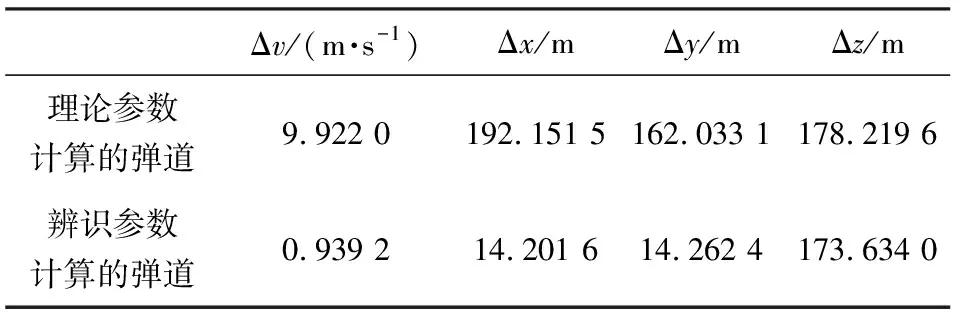
表3 状态偏差均值表

由图6及表3可得,分段辨识参数计算的弹道相比理论基准参数计算的弹道而言,其与雷达测量弹道的接近程度更高。因此,可认为分段辨识所得的阻力系数比基准阻力系数更为准确,从而说明结合使用NGN法与EKF法具有一定的应用意义。

4 结束语

本文首次将基于神经网络的参数辨识方法应用于弹丸的气动参数辨识。通过对仿真结果和实际辨识结果进行分析可得,当输入输出量测数据较为完整且网络的调整参数设置恰当时,NGN法能够以较高的精度及可靠性辨识出阻力系数;但当所获量测状态数据并不完整时,NGN法可用于补偿EKF法,提高其前期的辨识精度,从而满足工程应用要求。本文研究结果可为神经网络在弹丸气动参数辨识中的实际应用提供一定的理论参考。