基于二阶平滑的巡航导弹航路跟踪控制

路 浩,吝 科,石敏超

(空军西安飞行学院 理论训练系,西安 710306)

本文针对巡航导弹航路的精确跟踪问题,基于“提前转弯式”的航路段切换[1]的思想,把巡航导弹的航路平滑分解为多个相邻航路段的平滑过渡问题,将对称极多项式曲线引入到巡航导弹航路平滑过程中,生成满足巡航导弹性能约束的二阶平滑航路;然后采用反馈线性化方法建立巡航导弹线性化模型,基于“虚拟目标”的轨迹跟踪思想,将航路跟踪问题转化为对虚拟导弹的跟踪控制问题,设计了轨迹跟踪最优控制器;最后通过仿真验证了所提方法的有效性和优越性。

1 基于对称极多项式曲线的航路平滑

对称极多项式曲线计算简单,与直线段连接时曲率连续且有界,能够满足巡航导弹的性能约束,本文将对称极多项式曲线引入巡航导弹的航路平滑过程,生成可精确跟踪的平滑航路。

1.1 对称极多项式曲线

如图1所示的是平面上的一条对称极多项式曲线,图中O为极点,OA为极轴,(r,φ)为极坐标,R为曲线端点处的极径长,Φ为曲线的2个端点处的极径之间的夹角。

该对称极多项式曲线的方程[2]为

(1)

由式(1)可知,r(φ)=r(Φ-φ),曲线r=r(φ)关于φ=Φ/2对称,点(r,φ)处切线的方向角α和曲率κ分别为

(2)

(3)

式中:r′和r″分别为极径r对极角φ的一阶导数和二阶导数。由式(1)可得:

(4)

(5)

将φ=0和φ=Φ分别代入式(1)、式(4)和式(5),并根据式(3)可知,κ(0)和κ(Φ)均为0,则对称极多项式曲线与直线连接时,整条曲线满足曲率连续的条件。同时,对式(3)求导,得到曲率对极角的变化率为

(6)

式中:r‴为极径r对极角φ的三阶导数。可由r″求导得到:

(7)

则由极值定理和曲线的对称性可知,当φ=Φ/2,曲率κ取得最大值[2]:

(8)

1.2 三维航路平滑方法

航路规划算法得到的初始航路是由三维空间中的一系列航路点通过直线段连接而成的[3]。对于给定的初始航路{S,P1,P2,…,Pn,E},其中S为导弹发射点,E为目标点,三维坐标点Pi(xi,yi,zi),i=1,2,…,n,为巡航导弹的第i个中间航路点,如图2所示。

当巡航导弹沿着这种折线航路运动时,由于相邻航路段没有经过平滑处理,就会存在航路段切换的问题,即何时转弯飞往下一航路段。根据飞行过程中对中间航路点处理方式的不同,航路段切换方式可分为2种[1]:一是过点转弯,即当巡航导弹飞过一个航路段的终点后,调整航向飞往下一个航路段;二是提前转弯,即当巡航导弹接近一个航路段的终点时,调整航向飞往下一个航路段,如图3所示。

所谓“提前转弯式”的二阶航路平滑,就是用曲率连续且满足巡航导弹机动性能限制的曲线段航路替换存在夹角的相邻航路段的部分航路,使曲线和相邻的2个航路段相切,实现航路曲线的二阶平滑过渡,如图4所示。

由于相邻的航路段必定在同一个平面内,无论是二维航路平滑,还是三维航路平滑,都可以归结为确定平面上的对称极多项式曲线方程的问题。这样巡航导弹航路平滑就转化为在给定的最小转弯半径rmin条件下,建立极坐标系,并求解参数R和Φ的过程。

如图5所示,PiPi+1和Pi+1Pi+2是待平滑的相邻航路段;Pi,Pi+1和Pi+2在惯性系中的坐标分别为(xi,yi,zi),(xi+1,yi+1,zi+1)和(xi+2,yi+2,zi+2)。采用对称极多项式曲线对其进行平滑处理,首先定义巡航导弹曲线运动的平面为PiPi+1和Pi+1Pi+2所在直线确定的平面,则该平面的单位法向量bp为

(9)

式中:‖·‖表示向量的模。

以Pi为坐标系原点,tp=LPiPi+1/‖LPiPi+1‖为切向量,bp为副法向量,并通过右手定则得到主法向量np=bp×tp,建立曲线运动坐标系fp,该坐标系可表示为

fp=(tpnpbp)

(10)

在曲线运动坐标系fp下,航路点Pi的坐标值为(0,0,0)。根据坐标系fp和惯性坐标系之间的转换关系,可以得到航路点Pi+1和Pi+2在坐标系fp中的坐标值分别为

(11)

(12)

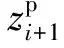
(13)

根据式(3)可知,对称极多项式曲线的2个端点处的切线与极径的夹角均为π/2,则对称极多项式曲线的参数Φ为

Φ=π-β

(14)

由于巡航导弹机动性能的限制,巡航导弹机动运动时有一个最小转弯半径rmin的限制,因此平滑航路的曲率半径必须大于或等于rmin,即:

(15)

为使平滑后航路与初始航路之间的偏差尽可能得小,选择κmax=1/rmin,则:

(16)

(17)

2 轨迹跟踪控制

在现代战争中,战场态势瞬息万变,为取得较好的攻击效果和较高的毁伤效能,常常对巡航导弹的打击时间进行较为明确的限制。那么,在航路跟踪过程中,巡航导弹所要跟踪的就是具有具体时间参数的期望航路,即进行轨迹跟踪。

2.1 巡航导弹线性化运动模型

根据文献[4],三维空间中的巡航导弹运动可用如下的仿射非线性系统描述:

(18)

式中:状态向量X=(xyzvψθ)T;(x,y,z)为巡航导弹在惯性坐标系中的位置;v,ψ和θ分别为巡航导弹的速度、弹道偏角和弹道倾角;控制向量u=(nxnynz)T,nx,ny和nz分别为巡航导弹过载在弹道坐标系各轴上的分量;f(X)和G(X)分别为

根据文献[5],系统(18)是可全状态反馈线性化的,则可以通过微分同胚:

(19)

和状态反馈变换:

(20)

使得系统(18)转换为如下的线性系统:

(21)

2.2 轨迹跟踪控制问题描述

航路跟踪控制问题主要研究如何控制巡航导弹使其沿预定航路飞行,以充分发挥航路规划的作用,保证飞行的安全性,提高巡航导弹的突防概率,是巡航导弹摧毁目标的关键。针对有明确时间要求的攻击任务,巡航导弹航路跟踪控制的目标就是采用某种控制策略,使导弹能够稳定地跟踪具有时间参数的飞行轨迹,尽可能地使巡航导弹与期望飞行轨迹之间的偏差最小。

如图6所示,空间曲线C表示巡航导弹的期望飞行轨迹,借鉴基于“虚拟目标”的轨迹跟踪的思想[6],假设有一个沿期望轨迹飞行的虚拟导弹,它在惯性坐标系中的位置和姿态可描述为(xd(t)yd(t)zd(t)vd(t)θd(t)ψd(t))T以导弹发射时刻为初始时刻,即t=0。为使虚拟导弹始终沿着期望轨迹飞行,则要求t=0时刻,虚拟导弹的初始位置位于航路起点,运动方向沿着规划航路的切线方向。在基于对称极多项式曲线的平滑航路上,直线段航路的方向角容易求得,曲线段航路的方向角则根据式(2)进行计算后转换到惯性坐标系中获得;而虚拟导弹的速度则根据作战任务的要求和平滑航路的长度进行确定,假设在攻击过程中虚拟导弹速度大小保持不变。那么,虚拟导弹的飞行轨迹,即巡航导弹所要跟踪的参考轨迹由下式产生:

(22)

若t时刻卫星定位系统和惯性导航系统实时测得的巡航导弹的实际位置为(x(t),y(t),z(t)),则轨迹跟踪控制的目标就是设计控制器使巡航导弹的实际位置和期望位置(xd(t),yd(t),zd(t))之间的偏差趋向于并保持为0。

2.3 轨迹跟踪控制器设计

根据前文描述,巡航导弹航路跟踪问题可以归结为对随时间变化的期望位置,即期望轨迹的跟踪问题。那么,本文所要解决的关键问题就是为巡航导弹设计跟踪控制器,使得:

(23)

式中:p(t)=(x(t)y(t)z(t))T为巡航导弹的实际位置;pd(t)=(xd(t)yd(t)zd(t))T为其期望位置。

定义跟踪误差e=(xe(t)ye(t)ze(t))T为惯性坐标系下巡航导弹当前位置和期望位置之差,即:

e=p-pd

(24)

(25)

将式(25)描述为状态空间形式,有:

(26)

(27)

由于系统(27)中x,y,z3个通道是相互独立的,为简化求解过程,可以为3个通道分别设计控制器,则系统(27)就转化为3个独立的系统:

(28)

根据最优控制理论,对于二次型性能指标:

(29)

由于系统(28)可控,最优控制量为

(30)

Pj(t)为二阶正定对称阵,满足黎卡提方程:

(31)

3 仿真实例

为验证本文方法的有效性和优越性,针对三维空间的航路点P1(0,500,200),P2(1 000,500,100)和P3(2 000,1 000,250),分别采用圆弧线和对称极多项式曲线进行航路平滑,并进行航路跟踪仿真。

图7分别给出了2种方法的平滑航路的局部水平投影,图8给出了2条航路的曲率曲线。从图中可以看出,对称极多项式曲线的曲率按照从0到最大值再到0的规律变化,能够实现与初始折线航路的二阶平滑过渡,符合巡航导弹的动力学特性;同时,由于在求解对称极多项式的过程中能够得到曲率最大值的显式表达式,进而对航路曲线最大曲率进行限制,所生成的平滑航路能够保证满足巡航导弹机动性能的约束。

巡航导弹初始位置位于P1点,初始速度方向指向P2点,最小转弯半径为1 km,速度变化范围为220～300 m/s,3个控制通道的惯性时间常数均为0.9 s,虚拟导弹的速度为260 m/s。图9分别给出了初始折线航路、圆弧线航路和对称极多项式航路上的实际跟踪轨迹;图10给出了法向过载变化曲线;图11给出了航路跟踪距离误差。

从仿真结果可以看出,在初始航路和圆弧线连接航路上,由于巡航导弹无法提供航路精确跟踪的需用过载,在航路的切换过程中产生了较大的轨迹跟踪误差。与之相比,在基于对称极多项式曲线的平滑航路上,由于航路平滑的过程中考虑到过载的约束和变化特性,在航路的过渡段巡航导弹能够提供轨迹跟踪所需过载,且能够获得虚拟导弹的位置、速度和加速度等信息,在非线性最优控制器的作用下能够保持对虚拟导弹的稳定跟踪,使得巡航导弹沿期望航路飞行。

4 结束语

航路曲线的曲率连续是巡航导弹能够精确跟踪的前提条件,是航路可飞性的重要保证。本文首先详细讨论并分析了对称极多项式曲线的几何特性,采用“提前转弯式”的航路平滑方法,把巡航导弹航路平滑问题分解为多个相邻航路段的平滑过渡问题,并将对称极多项式曲线引入航路平滑过程中,提出了一种基于对称极多项式曲线的平滑航路生成方法。然后采用基于微分几何理论的反馈线性化方法建立了巡航导弹精确线性化模型,降低了系统控制器设计的难度;针对有明确时间要求的攻击任务,假设存在一枚沿平滑航路运动的虚拟导弹,将巡航导弹航路跟踪问题转化为对虚拟导弹的跟踪控制问题,并采用线性二次最优控制理论设计了巡航导弹轨迹跟踪控制器。仿真结果表明,基于对称极多项式曲线的平滑航路曲率半径均满足导弹机动性能约束,且实现了飞行航路的二阶平滑过渡,进而能够实现巡航导弹对平滑航路的精确跟踪。