多阈值系统中的阈上随机共振研究
2019-01-03王友国翟其清
陈 楠,王友国,翟其清
(1.南京邮电大学理学院,江苏 南京 210046; 2.南京邮电大学通信与信息工程学院,江苏 南京 210003)
0 引言
在信号处理过程中,噪声的存在影响了有用信息的提取,所以人们一直致力于抑制噪声。然而在许多非线性系统中,噪声的存在却能够改善信息的传输,Benzi等人[1]在1981年首先观察到这个现象,并称之为随机共振(Stochastic Resonance,简称SR)。1995年,Collins[2]观察到了一种称为非周期性随机共振的新现象。2000年,Stocks[3]在继续Collins的研究中提出了阈上随机共振(Suprathreshold Stochastic Resonance,简称SSR)的概念,与SR不同,在SSR中当输入信号幅值大于阈值时也能观察到噪声增强。SSR的提出扩充了SR的理论,研究成果丰富[4-15]。
一直以来对于SSR及其应用的研究基本上都是基于阈值单元为二元输出的单阈值系统网络模型,其中Nikitin A等人[12]研究了该模型仅受乘性噪声影响时系统中的SSR现象,郭永峰等人[14]和李欢等人[15]则分析了该模型同时含有加性和乘性噪声时,系统中各参数对SSR现象产生的影响。但实际上该模型却可能存在更复杂的情况,例如每个阈值单元有多个输出。2009年,McDonnell等人[16]提出了随机池网络模型,这个灵活的模型可以捕获感官神经元的重要属性,并用来模拟真实的生物网络模型,能有助于人们进一步理解大脑的信号处理机制。基于这种网络模型,McDonnell等人[17]以信号量噪比为测度研究了具有加性噪声的多元输出阈值系统中的SSR现象,Cheng等人[18]则分别以互信息和信号量噪比为测度研究了具有乘性噪声的多元输出阈值系统中的SSR现象。因为在实际情况中,系统会同时受到加性噪声和乘性噪声的影响,所以本文在上述文献[17-18]的基础上以互信息为测度研究了在加性噪声与乘性噪声共同作用下多元输出阈值系统中的SSR现象。
1 多阈值系统网络模型
1.1 模型定义与符号说明
加性和乘性噪声共同作用下的多阈值系统网络模型如图1所示[18]。
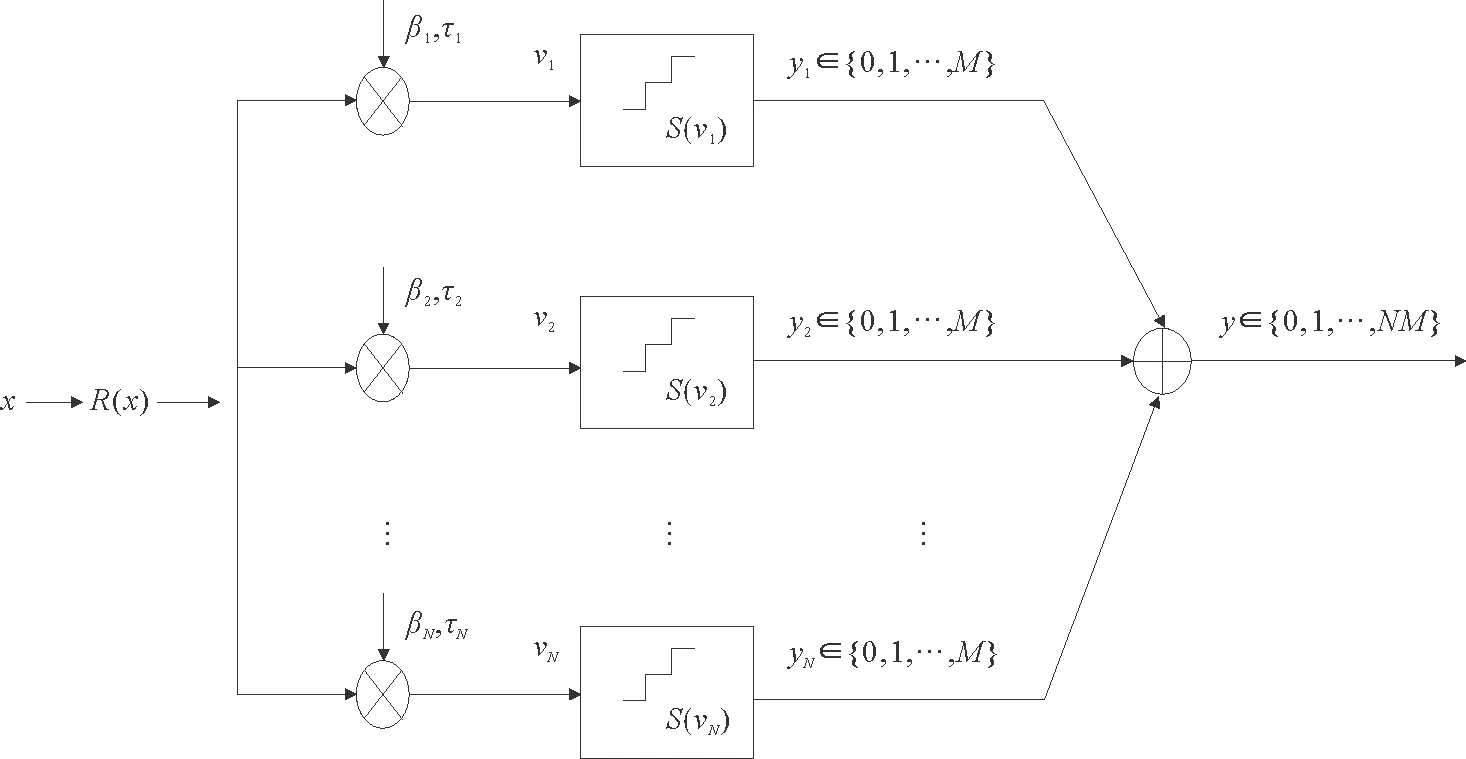
图1 多阈值系统网络模型Fig.1 Model of multilevel threshold Systems
该系统具有N个相互独立的阈值单元,且每个单元都有M个阈值δi,j,i=1,2,…,N,j=1,2,…,M,阈值单元的输出为yi∈{0,1,…,M},经过加性和乘性噪声共同作用下的输出vi可表示为
vi=R(x)+DβiR(x)+Qτi,i=1,2,…,N
(1)
其中,R(x)是系统函数,这里取其为分段函数[14]:
(2)
信号经过该系统函数的半波整流[19]后,只取信号中正的部分。βi、τi是相互独立的标准高斯噪声,D、Q分别是乘性噪声强度和加性噪声强度,即
(βi,βk)=0,(τi,τk)=0,(βi,τk)=0,i≠k
(3)
本文取输出函数为
S(x)=j,x∈[δi,j,δi,j+1),i=1,2,…,N,j=1,2,…,M
(4)
其中,δi,0=-∞,δi,M+1=+∞,把vi带入该函数可得S(vi)=yi,i=1,2,…,N。
当输入信号x为高斯信号时,其概率密度函数为
(5)
其中,输入信号x>0时,所满足的条件概率公式是高斯型的,可表示为
(6)
此时,每个单元的输出条件概率表达式为
(7)
当输入信号x≤0时,所满足的条件概率也是高斯型的,可表示为
(8)
此时,每个单元的输出条件概率表达式为
(9)

1.2 互信息
由Shannon信息理论,系统输出的互信息可表示为[12]
I=H(Y)-H(Y|X)
(10)
其中,H(Y)是输出熵,
(11)
式中的PY(n)为系统输出概率密度函数:

(12)
式中P(y=n|x)是给定输入信号x时输出y=n的条件概率密度函数,H(Y|X)为输入信号为x输出为y时系统损失的信息量(条件输出熵),
(13)
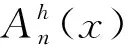
(14)
特别当h=1时,
(15)

(16)
2 数值计算与结果分析
为了便于研究,本文取σ=1,并且设定每个单元的阈值是均匀分布的,不同单元的阈值都相等,即
δ1,j=δ2,j=…=δN,j
(17)
则由式(10)可以计算出互信息I。图2~图6给出了在各系统参数下互信息I随不同噪声强度的变化。
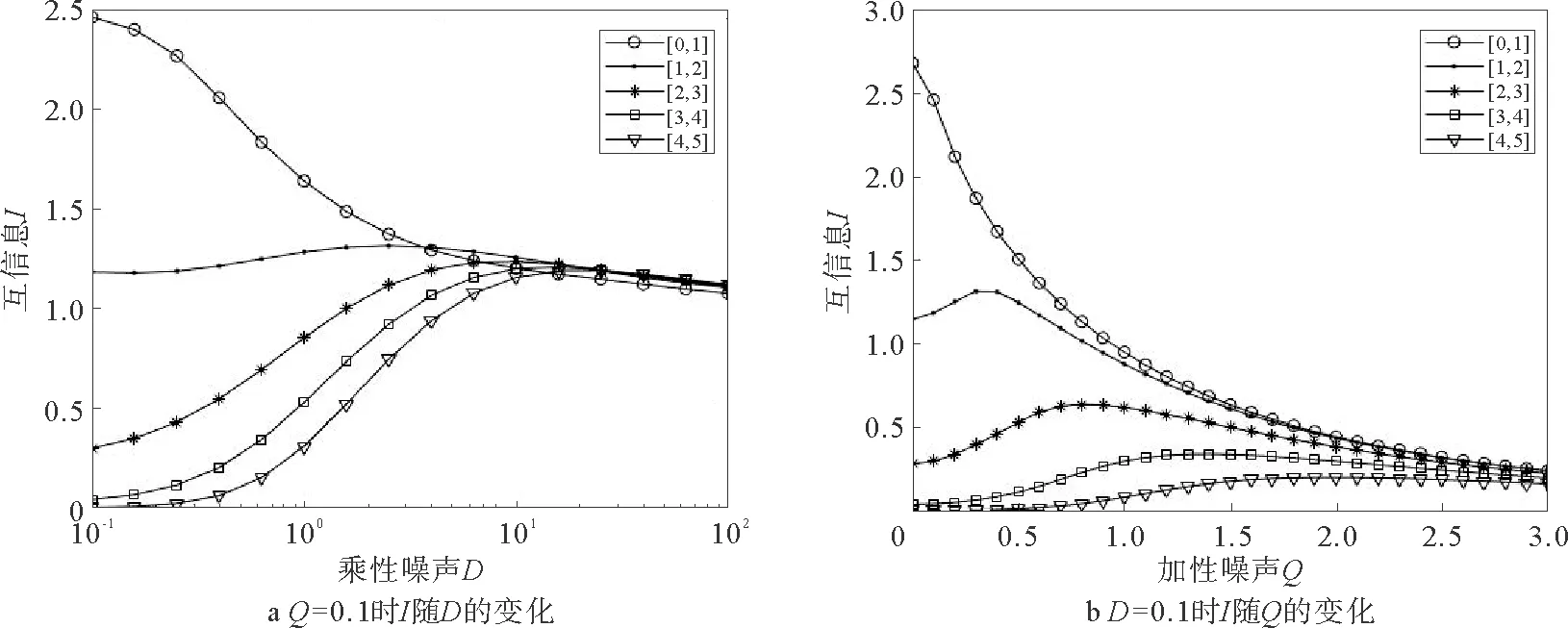
图2 M=8,N=16时不同阈值分布区间下互信息I随乘性噪声D和加性噪声Q的变化Fig.2 The mutual information I changes with multiplicative noise intensity D additive noise intensity and Q in different threshold distribution intervals (M=8,N=16)
设阈值单元数N=16,阈值单元输出元数M=8,在不同的阈值区间情况下,图2a给出了加性噪声强度固定为Q=0.1时,互信息随乘性噪声强度D变化的图像,图2b给出了乘性噪声强度固定为D=0.1时,互信息随加性噪声强度Q变化的图像。通过图2可以看到,对于端点值较小的阈值区间[0,1],互信息I随着乘性(加性)噪声强度D(Q)增加的变化曲线总是单调递减的,此时系统没有出现SSR现象;但是对于其他端点值较大的阈值区间,系统产生了SSR现象,曲线的顶点也随着端点值的增加而下移。图2表明阈值区间端点值的增大,即阈值的提高,使得系统中更容易产生SSR现象,但同时也会降低系统中信息传输的效果。这是因为阈值数值的提高使得系统中处于阈下的信号成分增加,SR现象的影响使得SSR现象更易产生,但阈值的增加也使得互信息达到峰值所需的相应噪声强度变大,噪声的增强恶化了系统中信息的传输,所以阈值的选择对改善系统中信息的传输很重要。
通过图2a与图2b的对比,可以发现相对于乘性噪声,加性噪声在互信息I达到峰值时的强度较低,即系统产生SSR现象时需要的加性噪声强度要比所需的乘性噪声强度要小,这表明对于加性噪声与乘性噪声,前者的改变会使得系统更易于产生SSR现象。
设阈值区间为[0,1],阈值单元数N=8,在不同的阈值单元输出元数M下,图3a给出了Q=0.01时互信息I随乘性噪声强度D的变化曲线,图3b给出了乘性噪声强度固定为D=0.01时,互信息I随加性噪声强度Q的变化曲线。通过图3可以看到,随着阈值单元输出元数M的增加,互信息I随乘性或加性噪声强度变化曲线的初始值和峰值也随之增大,但M=32与M=64时的两条曲线趋于重合,即互信息I在M的值增加到一定程度后趋于饱和。这是因为每个阈值单元输出元数越多,系统所输出的值就越多,但阈值单元输出元数的增加对系统中信息传输的增强是有限的。同时可以发现系统产生SSR现象所需的噪声强度也随着阈值单元输出元数的增加减小,SSR现象也越来越不明显,甚至当M的值过大(M≥16)时,系统中的SSR现象消失。这是因为对于固定的阈值区间,随着M的值增加,每个阈值单元的阈值δi,j越来越小。

图3 阈值分布区间为[0,1],N=8及不同阈值单元输出元数M时,互信息I随乘性噪声D和加性噪声Q的变化Fig.3 The mutual information I changes with multiplicative noise intensity D additive noise intensity and Q in different M (δi,j∈[0,1],N=8)
图3表明产生SSR现象所需的噪声强度与M的大小成反比,即在噪声强度较弱时,阈值单元为多元输出的阈值系统要比为二元输出的阈值系统更易使系统产生SSR现象,此时相对于二元输出的阈值系统,多元输出阈值系统中信息传输的效果更好。但当阈值单元输出元数过大时,SSR现象会消失,互信息I的值也趋于饱和。
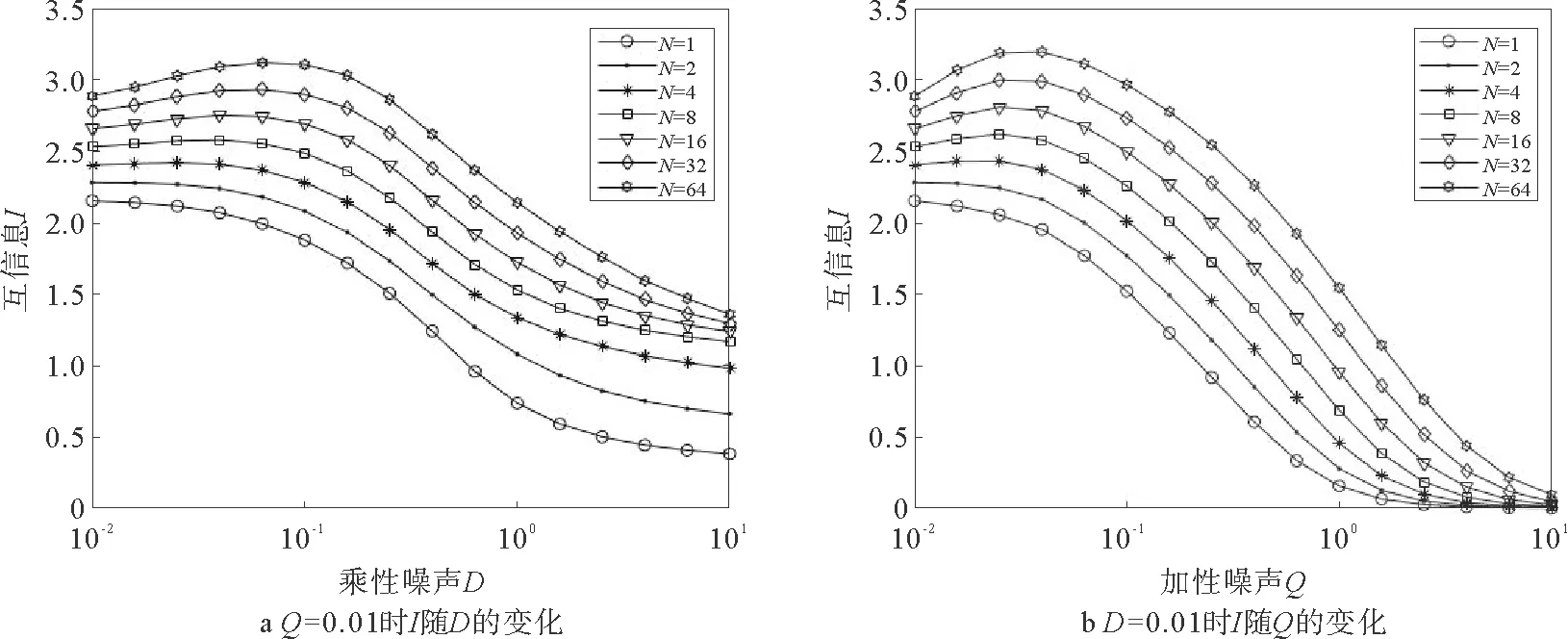
图4 阈值分布区间为[0,1],M=8及不同阈值单元数N时,互信息I随乘性噪声D和加性噪声Q的变化Fig.4 The mutual information I changes with multiplicative noise intensity D additive noise intensity and Q in different N (δi,j∈[0,1],M=8)
设阈值区间为[0,1],阈值单元输出元数M=8,在不同的阈值单元数N下,图4a给出了加性噪声强度固定为Q=0.01时互信息I随乘性噪声强度的变化曲线,图4b给出了乘性噪声强度固定为D=0.01时,互信息随加性噪声强度Q的变化曲线。通过图4可以看到,在N≤2时系统未出现SSR现象,而随着阈值单元数N的增加,系统产生的SSR现象越来越明显,互信息的峰值也随之增大。图4表明增加系统中的阈值单元数有利于系统中SSR现象的产生,并能够改善系统中信息的传输。
图5给出了在阈值区间为[0,1],M=4,N=32时,互信息I随着加性噪声强度Q与乘性噪声强度D的变化情况。通过图5可以看到在乘性噪声强度D固定,随着D的增加,互信息I随加性噪声强度Q变化曲线的上凸趋势越来越不明显,互信息I的峰值也随之减小。同时对于固定的加性噪声强度Q,随着Q的增加,互信息I随乘性噪声强度D变化的曲线逐渐由上凸趋势变为单调递减。

图5 阈值分布区间为[0,1],M=4,N=32时,互信息I随加性噪声强度Q与乘性噪声强度D的变化Fig.5 The mutual information I changes with both the additive noise intensity Q and the multiplicative noise intensity D (δi,j∈[0,1],M=4,N=32)

图6 阈值分布区间为[1,2],N=32,D=0.001时,互信息I在不同的阈值单元输出元数下随加性噪声强度Q的变化Fig.6 The mutual information I changes with additive noise intensity Q in different M (δi,j∈[1,2],N=32,D=0.001)
设阈值区间为[1,2],阈值单元数N=32,D=0.001时,在不同的阈值单元输出元数M下,图6给出了互信息I随加性噪声强度Q的变化曲线。通过图6可以看到,对于M=16,M=32与M=64时的3条曲线,互信息I随着加性噪声强度Q的增加出现了两个峰值,这表明系统出现了双峰阈上随机共振现象。
3 结论
本文以互信息为测度在文献[17-18]模型的基础上,通过对模型的数值计算与结果分析,发现在一定强度的加性噪声和乘性噪声共同作用下,多阈值系统中出现了阈上随机共振现象。并且该现象的产生还受阈值单元输出元数、阈值大小及阈值单元数的影响,提高阈值与增加阈值单元数都可以让系统更易于出现该现象,但是阈值的增加会减弱系统中信息传输的效果。此外,在噪声强度较弱时,提高阈值单元输出元数可以增强系统中信息传输的效果,但过高的输出元数会使系统中的阈上随机共振现象消失,并且使互信息的值趋于饱和。因此,阈值与阈值输出单元数的选择对于系统中阈上随机共振现象的产生以及信息传输的改善很重要。
