利用复杂网络技术分析地震活动性特征

张正帅,陈时军,周 晨,赵 瑞

(1.山东省地震局，济南 250014；2.黑龙江省地震局，哈尔滨 150000)

0 引言

地震活动时空分布往往表现出明显的非均匀性[1]。尽管大量的地震事件表现出较好的统计规律，用以刻画地震活动的总体规律，如描述余震衰减时间分布的Omori模型[2]以及随后发展的ETAS模型[3]，描述震级分布的Gutenberg-Richter震级频度关系[4]等。然而，地震事件时空分布往往表现出强烈的非独立、非随机分布的特性，使得这些统计规律的普适性受到挑战。进一步研究发现，不同地震事件之间存在着大时空范围的相互作用或相互关联[5]，一次强震的震源断裂错动所造成的应力场变化可能扰动其后的区域地震活动[6]。例如，美国兰德斯地震后诱发的距震中远达1 250 km的14个区域出现地震活动增强现象[1]等，表明地震活动时空分布具有明显的复杂性，而这种复杂性与地壳内存在的复杂构造体系以及复杂的动力学系统有关。近年来发展起来的复杂网络模型，大量用于研究自然科学、社会科学、工程技术等领域存在相互关联的复杂动力系统。复杂网络是对真实系统的抽象，它可以从整体的角度研究复杂系统的结构和功能，探究复杂系统内在的相互联系。复杂网络研究的开创性工作来源于Watts等[7]发现的真实网络具有小世界性质及Barabási等[8]发现的真实网络的无标度特性。复杂网络由此作为一种新理论受到科学界的大量关注，已经得到应用的领域涉及生物、电力、交通和社交网络等。近些年由Abe等[9-14]将复杂网络的概念引入到地震学研究之中，并做了大量工作，之后陆续有成果发表：2011年，谢周敏[15]利用加权复杂网络模型研究了地震网络的拓扑结构和动力学行为，2014年，何璇等[16-17]提出基于时空影响域的地震网络构造方法，2015年，赵海等[18]研究了美国南加州地区地震网络的规模和熵演化；2015年，李光光等[19]基于地震网络的k-核解析了地震活动分布特征。2017年，Denisse Pastén等[20]对智利南北两个地区的地震活动不同震级阈值，不同网格划分等情况的复杂网络分析，发现介数中心性的非普遍性；2018年，Soghra Rezaei等[21]对动态地震网络的偏好连接性进行了研究，寻找最容易被影响的地震节点。本文采用Abe等[12]提出的地震网络构造方法，将地震目录转换成基于多图的复杂网络，由此构造的网络表示地震活动的动态信息，通过对该复杂网络量化分析，探究地震活动的复杂性。

1 地震网络构造方法及数据

1.1 地震网络构造方法

地震网络构造方法如下：首先对研究区的经度、纬度和深度进行三维网格化，得到若干大小相等的地理立方单元，如图1所示。在所研究的时空范围内，若该地理单元内至少发生过1次地震(震中位于单元的地理范围内)，则将该地理单元抽象为地震网络中一个节点；若2次相继发生的地震震中处于不同的地理单元内，那么这两个节点间产生1条边；若2次相继发生的地震震中处于同一个地理单元内，那么该节点产生1个自环。网格大小的取值可依据地震定位精度以及网络的稳定性确定，谢周敏[15]认为，网格边长在5km至10km范围内变化时，其所构造的地震网络具备较好的稳定性[22]。根据本文所选资料的地震定位精度，每个网格的纬度、经度及深度大小分别选择为5km×5km×5km和10km×10km×10km进行研究，并对结果进行对比分析。

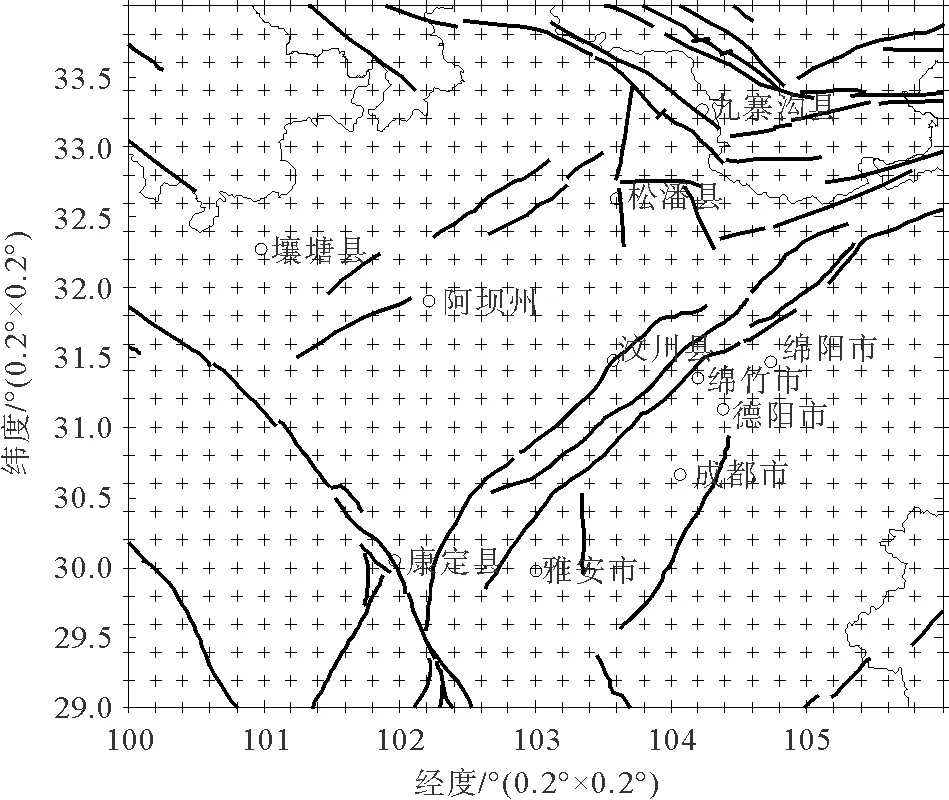
地理单元尺寸为0.2°×0.2°图1 研究区网格划分示意图Fig.1 A schematic description of meshing in the research region

度大于5图2 2013年地震网络拓扑结构Fig.2 Earthquake network topology in 2003

1.2 数据

研究地区位于青藏高原东缘，发育有多条活动断裂带。新生代以来，受青藏高原物质东南方向挤出作用影响而构造活动剧烈，GPS测量结果显示该地区现今地壳活动强烈且构造变形机制复杂。该地区是中国大陆最显著的地震活动区域之一，地震样本量大，为本研究提供了良好的数据基础。为分析该地区现代地震活动特征，本文选用研究区(29°N-34°N，100°E-106°E)2006年1月1日至2017年12月31日之间的地震目录构建地震网络，期间发生M0.0以上地震共计132 377次。由于地震网络是对真实地震现象的抽象，小震也会对整个复杂网络系统产生一定的影响，因此本研究不可忽略小地震样本。考虑到地震目录的完备性和一致性，根据刘丽芳等[23]，龙锋等[24]的研究，研究区内的最小完整性震级Mc=1.5左右，因此本文构造地震网络的震级下限取M1.5，震源深度取0km至80km，并剔除非天然地震事件，经过筛选，研究区范围10年内共计发生地震49 826次。本文构造地震网络采用的地震目录来自于国家地震科学数据共享中心(http://data.earthquake.cn)。图1为研究区网格划分示意图。作为示例，图2给出了2013年地震数据构造的地震网络，其中共有节点2 232个，边数6 734条，为了更直观展示地震网络的拓扑结构，图2中只给出了度大于5的节点予以显示。

2 地震网络结构特性

该部分对所构建的地震网络的特性予以研究。首先，分析地震网络的无标度特性；然后从地震网络的平均路径长度和聚类系数的考察中，分析了地震网络的小世界特性。地震网络本身是一种有向图，方向性对研究地震事件周期性(揭示在发生了多少次后续地震后，地震事件返回到初始节点)是重要的[25]。然而，考虑到本文在分析地震网络时，只关心节点间是否连通的静态特性；另外，当研究地震网络的小世界性质时，必须忽略方向性，并将路径长度定义为连接一对顶点的边数中可能最小的值[25]。本文将构造的地震网络转换为无向的简单图。首先移除网络中的自环，其次将两个节点之间存在的多边转换为单边，并且忽略边的指向。

2.1 无标度特性

无标度网络中大部分节点只有少数的连接，而某些节点却拥有与其他节点的大量连接，度分布满足幂律性，即P(k)～k-γ。P(k)是度值为k的节点出现的概率，其中幂指数γ为正指数，范围在1到2之间。本文通过最大似然估计方法计算得到幂指数。图3和图4给出了研究区2006年1月1日至2017年1月31日共10年尺度的地震网络度分布。其中图3、图4分别是网格大小为5km×5km×5km和10km×10km×10km的结果。

图3 节点度分布双对数曲线(网格大小为5km×5km×5km)Fig.3 The log-log plot of degree distribution with the cell size 5km×5km×5km

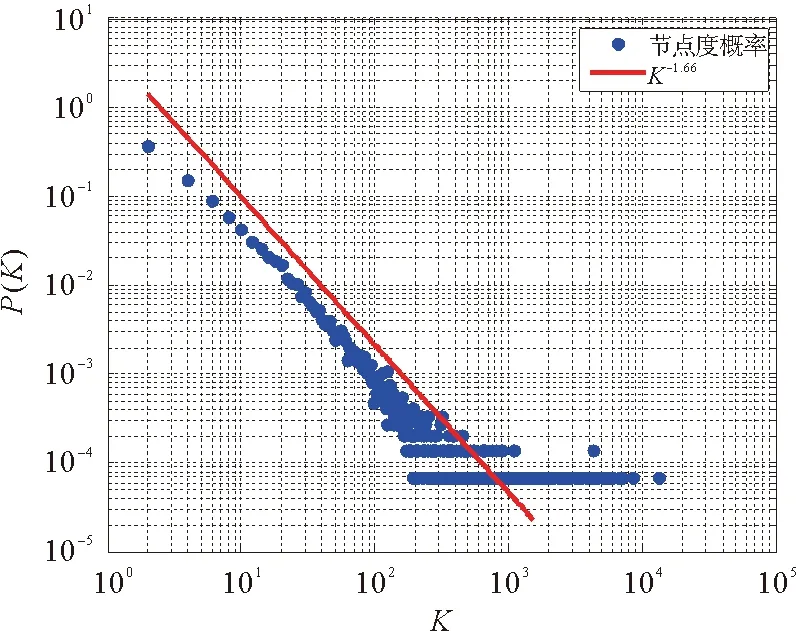
图4 节点度分布双对数曲线(网格大小为10km×10km×10km)Fig.4 The log-log plot of degree distribution with the cell size 10km×10km×10km

从图3、图4中可见，两种不同尺寸的网格所构造的地震网络的度分布P(k)满足幂律分布，显示该地震网络具有无标度特点。两个地震网络度分布都呈现幂律性，表明地震活动中震源之间的关联程度具有较强的异质性，即震源与震源之间关联程度很大与关联程度很小的各种情况都存在[15]。幂指数γ是有所差异的，γ越小，说明网络在度分布上的非均匀性越强，即某些中心节点的度越大；反之，度分布均匀性越强。相对来说以10km×10km×10km构造的地震网络比以5km×5km×5km构造的地震网络的度分布相对更均匀一点。两种网格尺寸下地震网络都是在大量地震事件统计意义下满足幂律性，地震网络都表现出较好的稳定性。另外，这种幂律性特征也说明不同地震事件之间互相作用蕴含深层的物理意义。

2.2 小世界特性

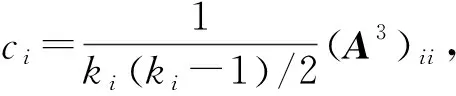
对比而言，根据所构建的地震网络节点数和边数随机产生的Erdös-Rényi随机网络模型(以下简称ER模型)，其网络中两个节点之间不论是否具有共同的邻居节点，其连接概率均为p，因此ER模型的聚类系数为：CER=〈k〉/(N-1)≈〈k〉/N=p≤1，其中〈k〉表示网络的平均度。因此，相比ER模型，具有小世界特性的网络具有更高的聚类系数。

具有小世界性质的网络平均路径长度L与ER模型一样具有较小的平均路径长度，由于ER模型的平均路径长度LER∝lnN/ln〈k〉，lnN随着N增长得很慢，使得即使规模很大的ER网络也具有很小的平均路径长度。表1给出了本文构建的地震网络与ER网络的参数对比。

表1 研究区地震网络与ER网络结构参数对比(2006年至2017年)Tab.1 The structure parameter comparison for earthquake network and ER network(2006—2017)

从表1可以看出，本文构建的地震网络相比ER网络具有明显的高聚类系数，而且两者之间都具有较短的平均路径，说明该地震网络具备小世界特性。

3 大震前后地震网络演化分析

就地震活动而言，地震的不断发生意味着地震网络结构不断发生改变，通过分析地震网络结构特性的演变，对探究大地震发生前后中小地震活动特征从而指导大地震预测具有重要减灾意义。结合Douglas等[27]提出的基于时间窗口的地震网络分析方法，本文设置时间窗口T，并以一定步长dT对地震目录进行滑动扫描，将每一个窗口所限定时间范围内的地震事件构造成一个新的地震网络，其中每个时间窗的窗尾作为窗口标志时间点，从而计算随窗口演化的地震网络特征参数值。

本研究主要考察研究地区M7.0以上地震前后的地震网络演化特征，包括2008年5月12日汶川M8.0地震、2013年4月20日芦山M7.0地震、2017年8月8日九寨沟M7.0地震。本文网格单元选择5km×5km×5km，窗口参数选择为T=10d，dT=1d，d表示天数。通过这样一组参数对地震前后6个月内地震活动数据进行滑动扫描计算，进行演化分析。

3.1 地震网络规模演化

地震网络的节点数和边数反映了网络的规模(大小)，是网络最直观的特征参量，所以首先考察地震前后网络规模的变化情况。图5、6、7分别给出了汶川M8.0地震，芦山M7.0地震和九寨沟M7.0地震的计算结果。其中，图a表示地震活动的M-T图(震级-时间图)。

从图5、6、7中的M-T图可以看出，无论是汶川地震，还是芦山地震与九寨沟，震前地震活动性比较均匀，难以发现明显的变化情况。根据网络规模演化分析，汶川M8.0地震前3个月，网络节点数和边数出现一定的增高—降低现象，而芦山M7.0地震、九寨沟M7.0地震前网络边数没有明显变化，但节点数存在明显的波动变化—降低的过程，表明网络规模的稳定性变差。然而，3个大地震之前的规模演化情况并不一致，所以仅仅通过网络规模的变化情况，很难提取到明显的异常信息，也就难以判断是否会发生大地震。但是，地震发生后，网络规模出现大尺度变化，且随着时间流逝，节点数和边数逐渐减少。这个现象与余震衰减规律是一致的，主要的物理机制在于大地震激发了弹性波能量的释放，进而触发大量余震，导致地震网络规模的变化，这也从复杂网络的角度对余震变化规律有了更深层次的理解。

3.2 k-核解析

Abe等[28]证明了地震网络具有层次结构。度小的节点群以分层的方式组织起来。然而，我们不清楚哪些节点属于哪个层，不同层之间的差异性还不够清晰。研究表明，随着网络规模的增长，其节点k-核值的变化会趋于稳定[29]，k-核值是一种更加稳定、简单的参数[30]。所以，为了获得网络层次的细节信息，本文利用k-core分解对网络进行解析，通过聚焦于地震网络最高核，研究最高核随时间的演化特征。

图5 汶川M8.0地震前后地震网络规模演化Fig.5 Scale evolution of the earthquake network before and after the Wenchuan M8.0 earthquake

图6 芦山M7.0地震前后地震网络规模演化Fig.6 Scale evolution of the earthquake network before and after the Lushan M7.0 earthquake

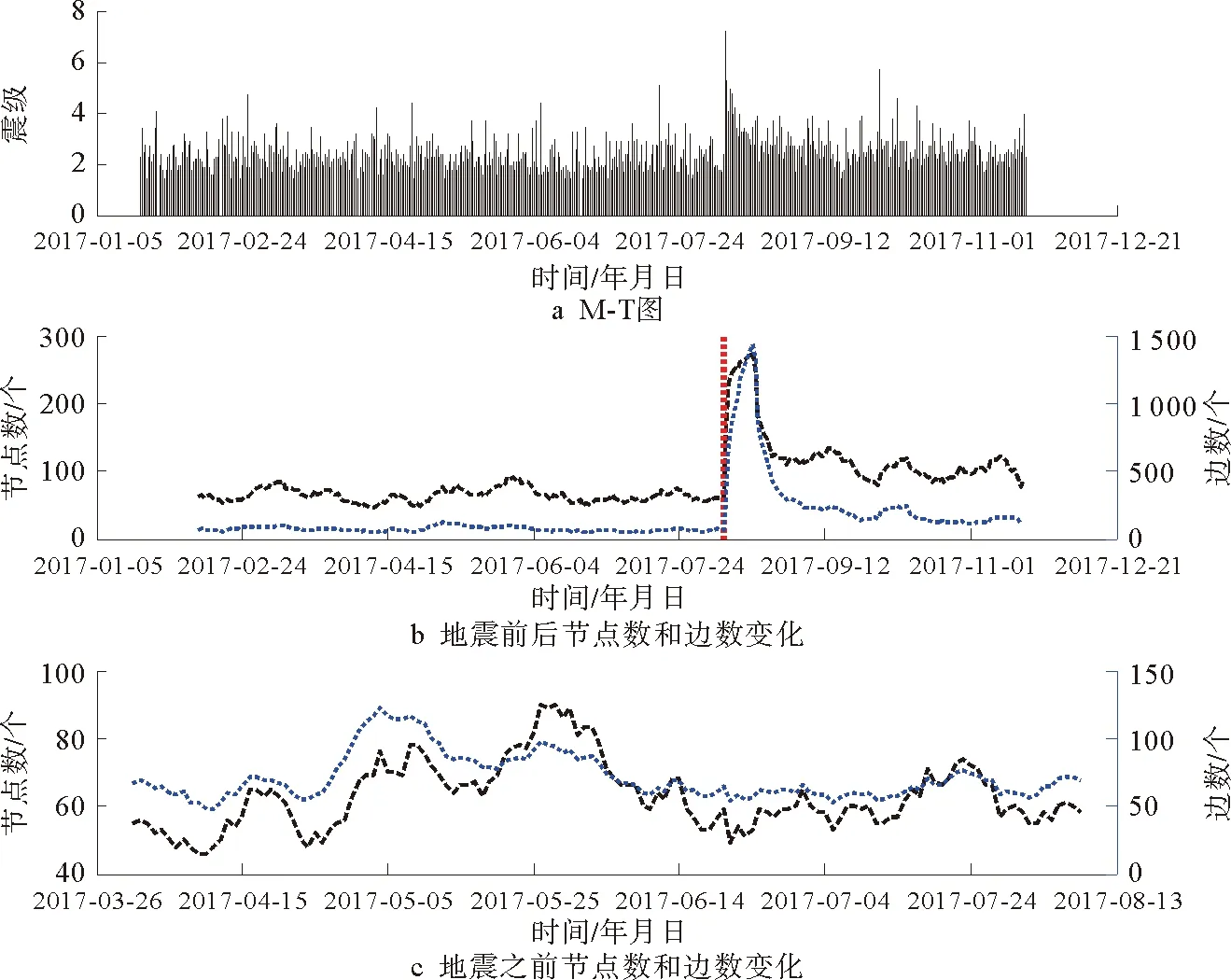
图7 九寨沟M7.0地震前后地震网络规模演化Fig.7 Scale evolution of the earthquake network before and after the Jiuzhaigou M7.0 earthquake

k-核是1983年由Seidman等[31]提出的一种简化网络拓扑结构的方法。k-核在复杂网络中的应用是由Gaertler等[32]以及Gkantsidis等[32]提出的，其定义为：一个网络图中的k-核是指反复去掉度数小于和等于k的节点后剩余的子图。节点的核数表示包含该节点的最深的核，即节点存在于k-核中，但是在(k+1)-核中被移除，则该节点的核数为k。因此可以通过k-核解析由外层至内层，一层一层地解析网络，从而揭示网络的层次结构性质。节点核数的最大值为网络的最大核数，也称最高核数[34]。在地震网络中，k-核的重要特点是节点的连通性，一个节点的核数越大，则通过该节点到达其他节点的路径就越多，也就是说这个节点的影响域更大。根据3.1部分选取的网格大小以及窗口参数，对地震前后数月内的地震网络进行最高核数计算，结果如图8所示。

图8给出了汶川M8.0地震、芦山M7.0地震、九寨沟M7.0地震期间，地震网络最高核数的演化量。对于芦山M7.0地震和九寨沟M7.0地震而言，震前3个月左右出现高值异常，且两者具有一定的相似性。震后最高核的值会逐步下降到5以下，恢复较为稳定的状态。但汶川M8.0地震前地震网络k-核并未出现明显异常，表明地震网络层次性结构可能未发生明显改变，这可能与汶川地震孕震范围大，亦或与汶川地震破裂方式、孕育环境等因素有关。由于网络层次性表现为度很小的节点具有高聚类系数，且属于高度连接的小模块，相反，度很高的节点具有低聚类系数，其作用是将不同模块连接起来[26]。大量实证研究表明，许多真实网络中节点的聚类系数与度存在近似的倒数关系[35-36]，说明复杂网络中聚类系数在一定程度上可以刻画网络的层次结构。为进一步描述这3次地震前后地震网络结构的层次特征，本文计算了上述3个地震前后几个月的地震网络聚类系数，结果如图9所示。

左箭头表示发震时间，黑色虚线表示最高核数均值线图8 地震网络最大核数的演化Fig.8 The evolution of the highest layer of the earthquake network

左箭头表示发震时间，黑色虚线表示平均聚类系数均值线图9 地震网络平均聚类系数演化Fig.9 The evolution of the average clustering coefficient of the earthquake network

从图9中可见，汶川M8.0地震前地震网络的平均聚类系数并没有发生大的波动，说明网络的层次结构未明显改变。所以，汶川地震之前，最高核数并未出现明显的异常特征。

4 结论与讨论

本文采用基于时间序列构造地震网络的方法，将研究地区的地震目录数据映射为一种复杂网络的形式，通过运用复杂网络的方法研究地震数据的统计规律，根据本文的研究可得到以下结论：

1)通过计算地震网络的聚类系数和最短路径长度，通过与同规模的ER随机网络相比，发现地震网络具有明显的高聚类系数及较短的平均路径的特点，说明地震网络的小世界特性。

2)度分布满足幂律分布，说明地震网络具有无标度特性。

3)汶川M8.0地震、芦山M7.0地震和九寨沟M7.0地震前3个月左右，网络规模稳定性有一定的扰动，其中汶川M8.0级地震前无论网络节点数和边数均出现小幅高值-降低的过程，而芦山M7.0级地震和九寨沟M7.0级地震前3个月内网络边数稳定但节点数存在波动升高-降低的过程。但是，仅仅通过网络规模的变化情况，很难提取到明显的大震前的异常信息。

4)大地震之后，网络规模有明显增大，节点数和边数在震后的数量显著增多，其主要原因在于主震触发了震区不同范围内的大量余震，对网络规模造成了影响，这也从复杂网络的角度说明了地震事件之间存在内在的动力学行为。

5)通过对k-核解析分析发现，芦山M7.0地震和九寨沟M7.0地震发生前地震网络的最高核存在显著的高值异常，但是，汶川地震之前未发现异常。通过对网络聚类系数的分析发现，可能的原因在于地震网络层次结构未发生变化。这与汶川地震的孕震条件、特定的地震动力学过程有一定相关性，值得进一步分析。

虽然本研究采用5km和10km尺度进行网格划分得到的结果是稳定的，但不同地区网格划分尺度需要进一步斟酌。此外，汶川地震前最高核变化未出现明显异常，而李光光等[19]在美国加州地区的计算结果也显示并不是所有大地震都能引起地震网络最高核数的异常变化。所以，考虑到单参数对地震网络特性描述的片面性，难以综合反映地震网络的动力学演化规律，因此在后续研究中建议考虑多参数融合分析，从而客观全面地探究震前地震活动异常特征。