ℤ2ℤ4[u]-加性循环码

耿 婕，吴化璋

(安徽大学 数学科学学院,安徽 合肥 230601)

0 引言

自20 世纪50 年代以来，二进制循环码一直被认为是最重要的一类纠错码[1]。20 世纪90 年代以来，有很多关于有限环上循环码的论文，读者可以查阅文献[2-5]等，以及其中的参考文献。同时，ℤ4上的循环码及其结构也得到了广泛的研究[6-8]。最近，环ℤ4被扩展到环ℤ4[u]上，ℤ4[u]中的循环码和重根常循环码[9-11]得到了研究。

一类将二进制线性码与四进制线性码结合起来的新型纠错码被称为 ℤ2ℤ4-加性码[12-14]。ℤ2ℤ4-加性码被定义为的子群。T.Abualrub等[15]引入了ℤ2ℤ4-循环码，并确定了这类循环码的生成多项式。最近,文献[16-17]中介绍了一类新的加性循环码:ℤ2ℤ2[u]-加性循环码。文献[18]讨论了ℤpℤp[u]-加性循环码的结构并得到了它们的最小生成集。文献[19]研究了ℤ2ℤ4[v]-加性循环码及其对偶码。

本文将ℤ2ℤ2[u]-加性循环码推广到ℤ2ℤ4[u]-加性循环码，其中u2=0。首先讨论ℤ2ℤ4[u]-加性码及其对偶码的一些性质；然后研究环ℤ2[x]∕＜xα-1 ＞×R[x]∕＜xβ-1 ＞中循环码的代数结构和最小生成集，其中R=ℤ4[u]。

1 预备知识

(1)C是一个加性码，且

(2) 对于任意码字u=(a0,a1,…,aα-1,b0,b1,…,bβ-1)∈C，它的循环移位

由Rα,β上的这种数乘运算，很容易得到下面的定理，这里省略它的证明。

定理1Rα,β是关于数乘*的R[x]-模。

类似[1]中关于循环码的讨论，将循环码C中的码字看作多项式或者向量。

定义2Rα,β的子集C叫做ℤ2ℤ4[u]-加性循环码当且仅当C是Rα,β的子群，且对C中所有元素c(x)=(a0+a1x+…+aα-1xα-1,b0+b1x+…+bβ-1xβ-1)，有

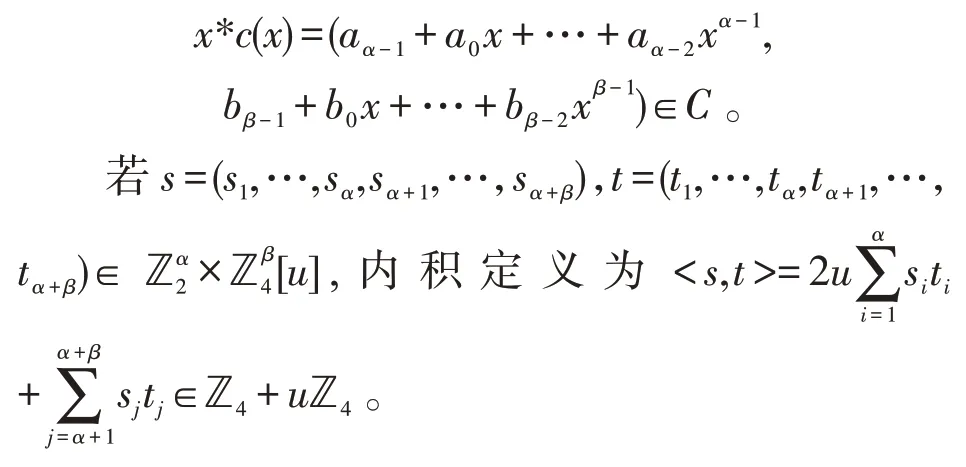
2 ℤ2ℤ4[u]-加性码的对偶

根据内积定义，C的对偶码定义为

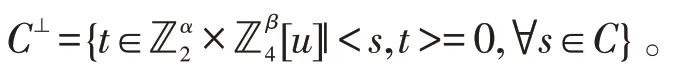
如果C⊂C⊥，码C称为自正交；如果C=C⊥，码C称为自对偶。利用上述对偶码的定义，有下面的定理。

定理2若C是ℤ2ℤ4[u]-加性循环码，则C⊥也是ℤ2ℤ4[u]-加性循环码。

其中j=lcm(α,β)。

3 ℤ2ℤ4[u]-加性循环码的结构

本节中，C是ℤ2ℤ4[u]-加性循环码。定义映射

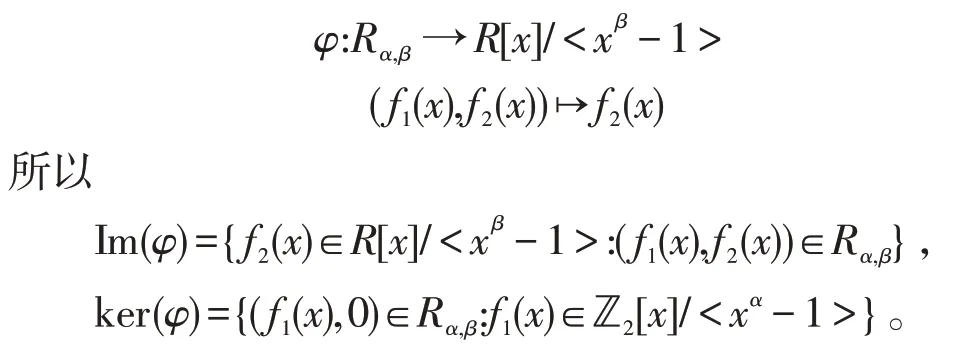
显然，φ是模同态，它的像Im(φ) 是R[x]∕＜xβ-1 ＞的子模，核ker(φ)是Rα,β的子模。此外，Im(φ)可被看作是环R[x]∕＜xβ-1 ＞的理想。根据文献[20]，得到下面结论。

定 理3设Im(φ) 是ℤ4[u] -循环码，则Im(φ)=(g(x)+up(x),uq(x))，其中g(x),p(x),q(x)∈ℤ4[x]∕＜xβ-1 ＞,q(x)|g(x)|(xβ-1),q(x)|。

定理4设Im(φ)=(g(x)+up(x),uq(x))是ℤ4[u]-加性循环码。若q(x)是ℤ4[x]∕＜xβ-1 ＞上首一多项式，则deg(p(x))＜deg(q(x))。

引理2设Im(φ)=(g(x)+up(x),uq(x))是ℤ4[u]-循环码。若g(x)=q(x) 则Im(φ)=(g(x)+up(x)) 。此外，若q(x) 是ℤ4[x]∕＜xβ-1 ＞上首一多项式，则(g(x)+up(x))|(xβ-1)。

定义集合 ：I={f(x)∈ℤ2[x]∕＜xα-1 ＞|(f(x),0)∈ker(φ)}。显然集合I是环ℤ2[x]∕＜xα-1 ＞上的理想和循环码。根据第一同构定理，有

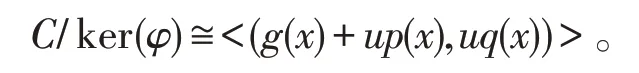
类似于[15]中对ℤ2ℤ4[u]-加性循环码的讨论，有下面结论。

推论2设C是ℤ2ℤ4[u]-循环码,则

其中f(x),l1(x)∈ℤ2[x]∕＜xα-1 ＞,q(x)|g(x)|(xβ-1),，并 且 deg(p(x))＜deg(q(x)),deg(li(x))＜deg(f(x))。

接下来确定Rα,β中循环码的最小生成集，有如下结果。

定理 5设C=＜(f(x),0),(l1(x),g(x)+up(x)),(l2(x),uq(x))＞是ℤ2ℤ4[u] -循环码。若deg(f(x))=t1,deg(g(x))=t2,deg(q(x))=t3,h(x)=(xβ-1)∕g(x)，则C的最小生成集是S=S1∪S2∪S3∪S4,其中

4 结束语

本文讨论了ℤ2ℤ4[u]-加性码及其对偶码的一些性质，这里u2=0 。主要研究环ℤ2[x]∕＜xα-1 ＞×R[x]∕＜xβ-1 ＞中循环码的代数结构和最小生成集，其中R=ℤ4[u] 。后期将研究ℤ2ℤ4[u]-斜准循环码。