新型社交网络谣言传播演化模型研究
2019-01-03刘万平刘小洋黄诗雯
吴 晓,刘万平,杨 武,卢 玲,刘小洋,黄诗雯
(重庆理工大学计算机科学与工程学院,重庆 400054)
0 引言
谣言的传播经久不衰,是近年来国内外学者研究的热门课题[1]。谣言会引发社会混乱,导致社会危机,使得民心动乱,造成经济动荡。网络谣言不同于传统谣言,它是伴随着网络发展而出现的。网络谣言指的是一类在互联网中以网络特有的方式,在用户与用户之间传播含有公众所关注的事件、社会现象和问题的吸引力信息。这类消息是一种特殊的陈述,而其真实性含有模糊性或严重失实。
互联网的日渐普及甚至日常化,将当代中国社会带入一个网络快速发展的时代,同时各类网络应用软件应运而生,使得网络用户的数量呈现一种前所未有的增长趋势。其中社交网络用户通过微博、微信和QQ等社交软件来获取资讯。因为社交网络消息传播速度快的特点,网络谣言变得愈发难以控制。网络用户的注册信息不完善使得造谣传谣者无法切身考虑其行为所带来的后果,社交媒体实时交互消息,消息传播多样化,以上原因导致社交媒体成为网络谣言诞生与传播的温床。
谣言与互联网相结合后,较传统的谣言有了很大区别,也产生许多新特点。谣言传播的传播机理与传染病有很大的相似性,因此,前人的谣言传播类型有很大一部分是基于SI、SIS和SIR等经典的传染病模型建立的[2]。模型的研究出现于20世纪60年代,由Daley和Kendall提出的DK模型是公认的谣言传播模型[3]。当特别考虑网络谣言在社交网络中的传播时,发现网络谣言许多新的特征,这些特征与社交网络的结构以及一些特性具有很大的相关性[4-7]。谣言传播区别于疾病传播的最独特属性为传播途径的不同。当社交网络与谣言传播相结合时,谣言将会以更快的速度进行传播,且因网络结构而出现多层次的传播现象,无法彻底切断谣言的传播途径。网络谣言传播跟疾病传播的最大的区别为传播途径的不同。因此谣言传播需要考虑网络结构特征[8-10]。依据平均场理论和网络谣言的各个特征建立详细的动力学传播模型[11-13],而后在社交网络结构上实验验证模型的可靠性。用户节点都会存在一个缓存,用户节点类似于一个接收设备,大量消息会传播到这个设备导致不能完全处理,使得消息存在延时处理或忽略的情况,这种状态称为消息缓存。由于消息缓存,消息会存在被阅读或者延迟阅读的情况。因此考虑上述情况增加一个新状态R(接收未处理状态)。文章同时考虑谣言的澄清,用户文化程度以及遗忘率等因素,基于平均场理论建立了URBD模型。本文的第2节通过建立社交网络谣言传播模型,得出谣言传播的微分动力学方程;第3节对谣言的传播过程以及传播模型的临界值进行分析;第4节通过数值实验分析谣言传播的特点;第5节针对社交网络谣言传播得出结论。
1 模型建立
网络谣言的传播特性与生物病毒、恶意软件[14-17]以及流行病的扩散有一些相似之处,但是网络谣言主要是通过社交网络进行传播,因此具有一些不同的特点。文章通过建立一个全新的网络谣言传播模型来研究影响社交网络谣言传播的关键因素[18-20]。以及尝试得到网络谣言的控制方法。用户文化程度对谣言传播有明显的影响,不同的文化程度对于谣言的鉴别能力是不同的。因为用户具有遗忘特性,随着时间推移,接触过谣言的用户会在一定程度上遗忘甚至彻底遗忘谣言内容[21-22]。因此,模型设置一定的遗忘率来刻画真实的谣言传播。另外谣言支持用户因为政府或者一些公众人物的谣言澄清,他们会认识到谣言,进而转变为谣言反对用户。此外考虑到网络谣言在社交网络中具有的新的特性即消息缓存,这个特点对谣言的继续传播具有很大的关系,所以在模型当中添加一种新的状态来描述消息缓存。
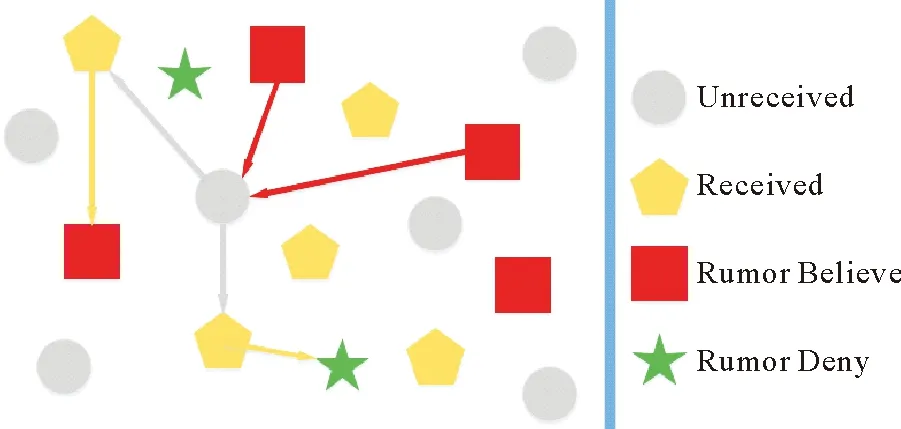
图1 谣言传播示意图Fig.1 Schematic diagram of rumor spreading
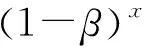
1)未接收状态(Unreceived):该状态指使用社交媒体用户的账号尚未接收到网络谣言,即对应节点处于未接收谣言状态,处于该状态的节点记为U节点。
2)接收未处理状态(Received):该状态指用户已经接收到谣言或者用户关注的群体已经发布或转发了谣言,但是由于用户暂时未使用社交媒体软件,尚未阅读到该谣言时的状态。处于该状态的节点记为R节点。
3)谣言支持状态(Rumor Believe):用户在社交媒体中阅读到该条谣言,并且认同和相信该条谣言,进而以一定的概率传播这条谣言的状态,处于该状态的节点记为B节点。
4)谣言反对状态(Rumor Deny):从社交媒体中阅读到该条谣言,但是对于谣言持反对的态度,并且有一定的机率去传播辟谣消息的状态,处于该状态的节点记为D节点。
首先考虑所有注册用户都是U节点,并且整个社交媒体的用户数量N(t)是保持不变的,为方便起见,将社交网络谣言传播模型里面一些符号作如下说明:
1)U(t):U节点在t时刻的数量,即未接收到谣言的用户在t时刻的数量。
2)R(t):R节点在t时刻的数量,即消息缓存中已接收到谣言但还未阅读的用户在t时刻的数量。
3)B(t):B节点在t时刻的数量,即阅读消息缓存同时看到谣言且对谣言持支持态度的用户在t时刻的数量。
4)D(t):D节点在t时刻的数量,即阅读未读消息同时看到谣言且对持反对态度的用户在t时刻的数量。
5)N(t):全部注册的社交媒体用户在t时刻的数量,整个社交媒体用户数量N(t)=U(t)+R(t)+B(t)+D(t)。
对于建立模型所需要的一些假设和参数描述如下:
1)所有没有接收到谣言的社交媒体用户都是U节点。
2)所有的U节点在理论上以概率[1-(1-β)B(t)]会成为谣言的R节点,概率[1-(1-β)B(t)]与用户拥有的消息来源数目有关,即与U节点所关注的用户当中是B节点的数量有关。此外U节点所关注的用户的文化程度也是U节点成为R节点的决定因素,当在用户关注的用户文化程度低的情况下,关注列表中会存在较多的B节点。转换率的影响因素还与U节点的活跃度有关系,当U节点活跃度较高时,对于未处理的消息会有较高的阅读率,从而谣言被延迟阅读的概率降低,导致单位时间内R节点转化为B节点和D节点的转化率升高。
3)R节点在阅读社交媒体的消息后,会以概率αb和αd分别转换成为B节点和D节点。由于用户文化程度的影响,高教育程度的R节点会对消息中的谣言进行识别或者R节点因曾了解过类似的谣言,自然成为D节点,这些原因共同影响着参数αd的大小。同时对参数αb来说,低教育程度的R节点会轻易相信谣言,当R节点通过传播网络谣言可以获得利益时,R节点会选择相信并转发,成为B节点。
4)受辟谣工作的影响,B节点会以概率γ转换为D节点。辟谣主要是政府机构、各大新闻媒体以及网络大V发表的一些关于谣言的知识普及或者关于谣言的真实新闻,使得用户认识到谣言。
5)考虑到用户的遗忘性质,用户节点会以概率f转换为U节点。因为用户处在一个信息快速交互的互联网时代,信息多种多样且层出不穷,所以用户将逐渐遗忘谣言。谣言遗忘率还同用户的关注、社会的热度以及谣言存在的时间长短有非常大的关系。
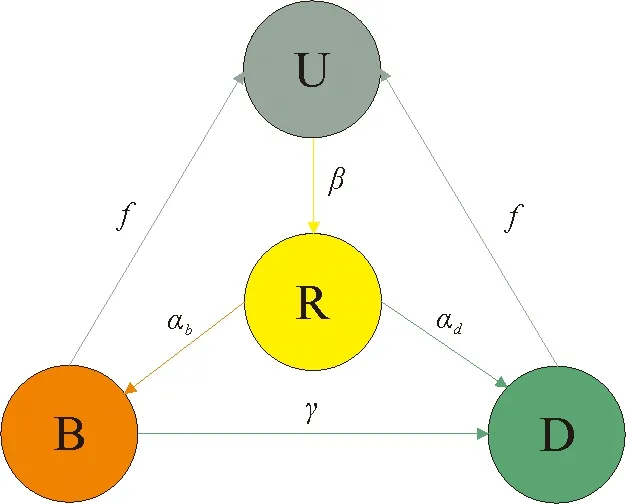
图2 网络谣言状态转化示意图Fig.2 General schematic of the new model with different transform rates
整个社交网络谣言模型的示意图和各个类型用户的转换率以及转换方向如图2网络谣言传播状态转移示意图所示。
首先建立模型,整个社交网络先视为全连接网络,通过使用微分动力学方程来表示整个模型,所以可以得到的系统(1)[21]:
(1)
对系统(1)进行分析,发现两项同类型的可以进行简化的项1-(1-β)B(t)和1-(1-γ)D(t),令Pβ=1-(1-β)B(t)以及Pγ=1-(1-γ)D(t),可以表示为f(x,y)=1-(1-x)y,x∈[0,1],y≥0,y代表B(t)和D(t)。对f(x,y)做关于B(t)和D(t)的实验,得到如下的结论(如图3所示),通过分析f(x,y)关于B(t)和D(t)的函数。可以看到f(x,y)随着B(t)或D(t)的增长迅速到达上界。
通常社交网络的节点个数数以万计,因此我们合理设置Pβ和Pγ分别为βΛB(t)和γΛD(t)。通过参数形式的改写,假设的全连接网络形成一个随机的稀疏网络。这使得模型又具有一些属性(如稀疏性),可以更好描述实际的社交网络。
因此系统(1)可以被改写为
(2)
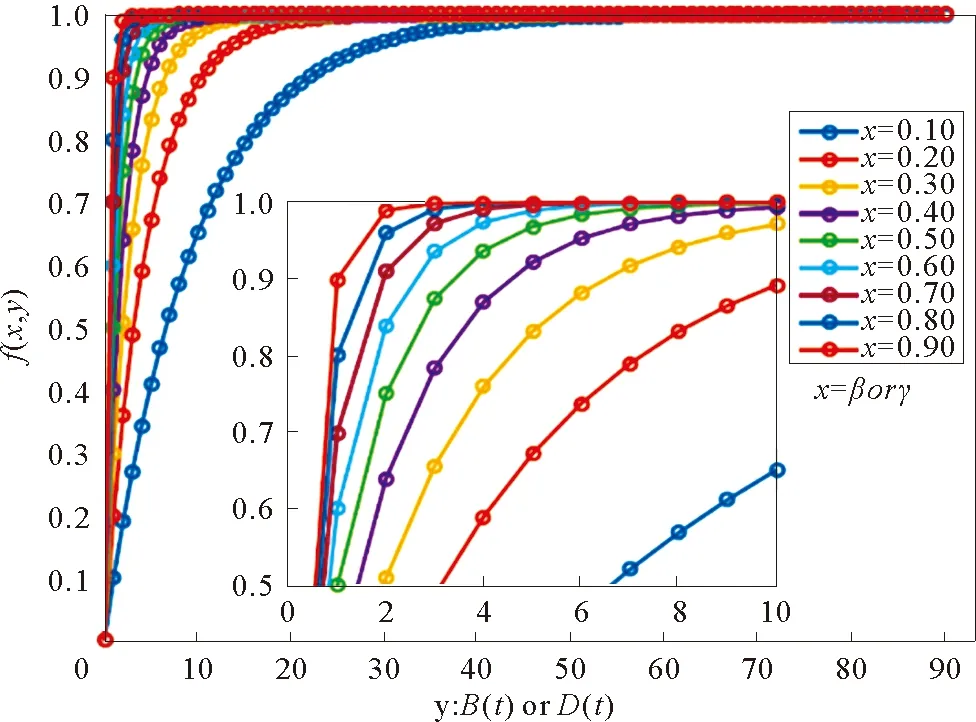
图3 函数f(x,y)的数值演化示意图Fig.3 Numerical evolutions of the function f(x,y)
为了方便后续分析提出一些符号标识。
1)u(t):表示在t时刻整个模型U节点的密度,u(t)=U(t)/N(t)。
2)r(t):表示在t时刻整个模型R节点的密度,r(t)=R(t)/N(t)。
3)b(t):表示在t时刻整个模型B节点的密度,b(t)=B(t)/N(t)。
4)d(t):表示在t时刻整个模型D节点的密度,d(t)=D(t)/N(t)。
全部的普通用户构成了N(t),假设整个社交媒体网络基本用户数目是不变的。因此N(t)的数量在任何时刻始终等于N,N就是所有社交媒体网络的用户。
设置Λ=1/N,于是上述模型可以简化为
(3)
由于u(t)+r(t)+b(t)+d(t)=1,因此系统(3)等价于系统(4)。
(4)
网络谣言的传播阈值就是一个谣言支持用户在它信谣阶段使得普通用户转变为谣言支持用户的平均数。根据Driessche和Warmough[25]提出的计算传播阈值的方法,可以计算出模型(4)传播阈值为R0=αbβ/f(αb+αd)。
2 模型分析
在这一部分,将计算网络谣言传播模型的平衡点,以及使用Lyapunov方法[26]分析平衡点的局部稳定性和全局稳定性。平衡点是系统可能达到稳定的一个状态。在现实系统中,通常可以控制相关的因素使系统达到平衡点的状态。若平衡点是稳定的,系统将会保持这种稳定状态,不会再有各类节点数量的变化。相对于社交网络谣言,使整个在线社交网络谣言传播系统快速达到稳定的平衡点,即可达到快速控制谣言发展的效果,也可缩减不必要的人力物力。
经计算系统始终存在一个无谣言平衡点E0=(0,0,0)。
定理1根据系统(4),得到如下结论。
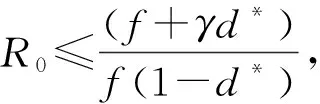
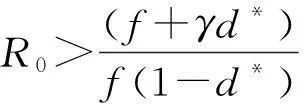
证明: 设(r*,b*,d*)(r*>0,b*>0,d*>0)是系统(4)的一个谣言平衡点,则
βb*(1-r*-d*-b*)-αdr*-αbr*=0αbr*-fb*-γd*b*=0αdr*-fd*+γd*b*=0
(5)
由(5)的第一个等式得到
(6)
将(6)代入(5)的第二个等式,可以得到
b*[αbβ(1-b*-d*)-(f+γd*)(αb+αd+βb*)]=0
(7)
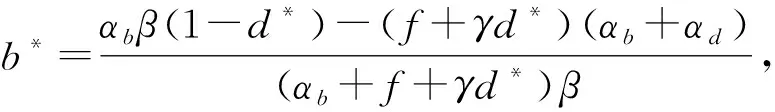
通过将b*代入(5)第三个等式,得到如下方程:
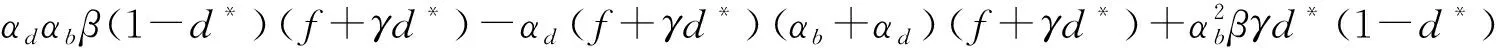
(8)
令θ1=αbβ,θ2=αb+αd,得如下方程
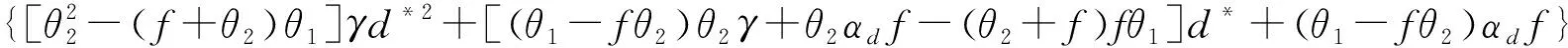
(9)
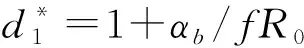
定理2当R0≤1,系统(4)的无谣言平衡点是局部稳定的。
证明: 无谣言状态时系统(4)对应的Jacobian矩阵如下所示
因此对应的特征方程为(f+λ)[(αb+αd+λ)(f+λ)-βαb]=0,求得λ1=-f,以及λ2,λ3。根据c/a=f(αb+αd)-βαb,b/a=αb+αd+f。因R0≤1,得λ2,λ3均为负。根据Hurwitz定理[26],当R0≤1时特征方程的根是负根。根据Lyapunov方法得到E0无谣言平衡点是局部稳定的,定理2得证。
定理3若R0≤1,则系统(4)的无谣言平衡点E0是全局稳定的。
证明: 定义正定二次函数V(r,b,d)=r(t)+ω1b(t)+ω2d(t),其中ω1=β/f,ω2=αb(f-β)/f(αd+γ)。则:
=βb(t)(1-r(t)-b(t)-d(t))-(αb+αd)r(t)+ω1(αbr(t)-fb(t)-γb(t)d(t))
+ω2(αdr(t)-fd(t)+γb(t)d(t))
=βb(t)-βb(t)r(t)-βb2(t)-βb(t)d(t)-(αb+αd)r(t)+ω1αbr(t)-ω1fb(t)
-ω1γb(t)d(t)+ω2αdr(t)-ω2fd(t)+ω2γb(t)d(t)
=(β-ω1f)b(t)+(ω2γ-ω1γ-β)b(t)d(t)+(ω1αb+ω2αd-(αb+αd))r(t)
-βb(t)r(t)-βb2(t)-ω2fd(t)≤0
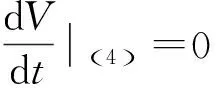
定理4若R0>(f+γd*)/f(1-d*),则系统(4)的谣言平衡点E*在Ω
证明: 令u*=1-r*-b*-d*,定义二次函数
其中ω1=(f+β)/αb,ω2=f/αd。计算可得
=(ω1αb+ω1b*αb+ω1b*f-fu*+ω2d*αd)b+(ω1b*αb+ω2αd+ω2d*αd+ω2d*f-fu*)d
+(ω1b*αb+ω2d*αd)u+(ω1b*γ+ω2d*γ-ω1αb-ω2αd)bd+(f+βu*-ω1αb)bu+(f-ω2αd)du
-(ω1αb+ω1f)b2-(ω2αd+ω2f)d2-ω1γdb2-ω2γbd2-βbu2-ω1b*αb-ω2d*αd≤0
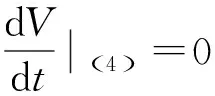
3 数值实验
在这一部分,将通过数值实验来验证第三部分结论的准确性。通过实验分析准确性后,依据现实因素提出控制社交网络谣言传播的方法以及指导性的建议,为净化网络空间构建文明网络做出努力。为快速得到实验结果,我们使系统(4)处在一个谣言传播的过程当中而非网络谣言开始传播初始阶段,即u(0)>0,b(0)>0和d(0)>0。
实验1对于系统(4),令f=0.14,β=0.3,γ=0.2,αb=0.3和αd=0.6。计算得到无谣言平衡点E0=(0,0,0)以及R0=0.714 3(R0<1),接着通过数值实验证明定理3无谣言平衡点E0是全局稳定的。
根据实验1的参数值初始值,图4a展示了20个不同初始值情况下谣言传播情况,其中方框代表初始值以及红圈代表无谣言状态E0=(0,0,0)。从图中能够看到不同初始值情况下的系统都发展并到达了无谣言平衡状态E0=(0,0,0),也证明了定理2。对于一组系统初始值r(0)=0.10,b(0)=0.60,d(0)=0.20,图4b展示了r(t),b(t)和d(t)的占比情况,它是谣言传播中的一组给定初始值的节点平均占比的演化曲线,从这里也可以看出无谣言状态会使得U节点最终趋近于1,同样与E0=(0,0,0)相吻合。
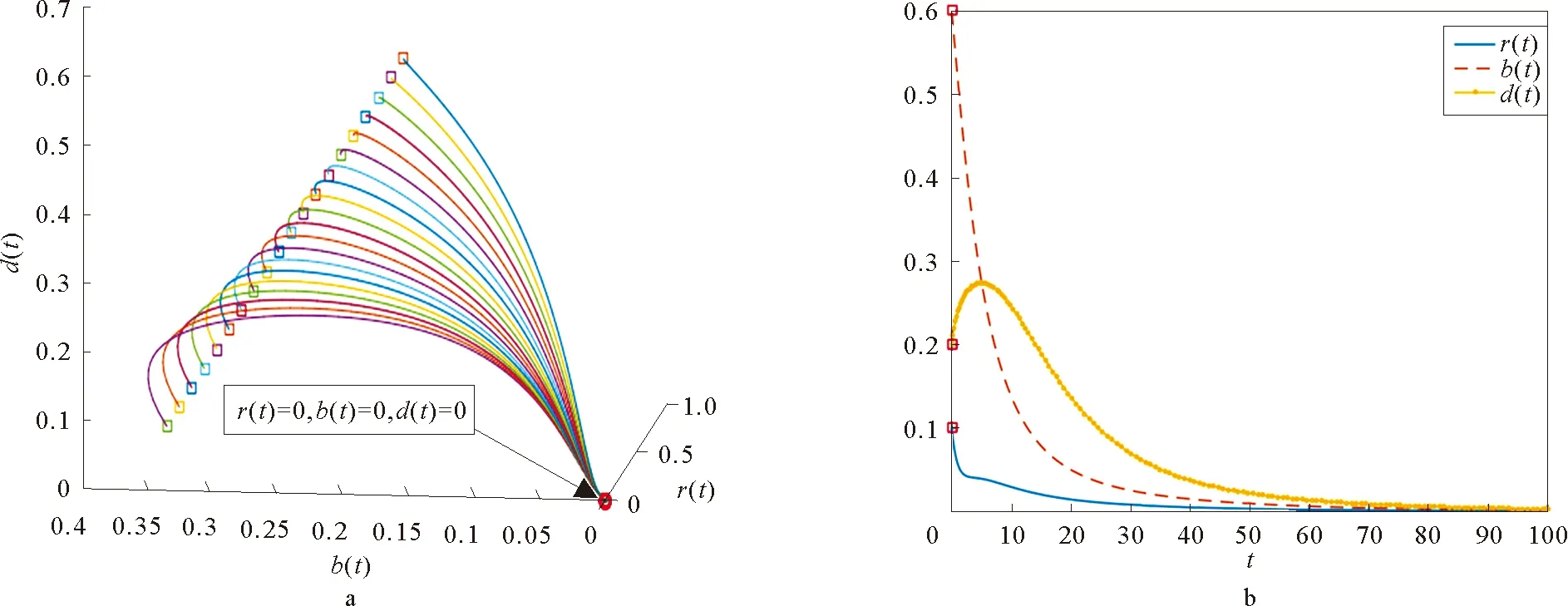
图4 无谣言状态图Fig.4 No romor state diagram
实验2系统(4),令f=0.14,β=0.8,γ=0.5,αb=0.25和αd=0.5。然后根据公式R0=αbβ/f(αb+αd)计算得出R0=1.904 8,R0>(f+γd*)/f(1-d*)以及定理4谣言平衡点E*=(0.033 4,0.040 0,0.139 7)是渐进稳定的。
根据实验2的参数初始值,图5a展示了20个不同初始值情况下谣言传播情况,其中方框代表初始值以及红圈代表谣言状态E*=(0.033 4,0.040 0,0.139 7)。从图中可以看到不同初始值情况下的系统都发展并到达了谣言平衡状态E*=(0.033 4,0.040 0,0.139 7)。对于一组系统初始值r(0)=0.10,b(0)=0.60,d(0)=0.20,图5b展示了r(t),b(t)和d(t)的占比情况,它是谣言传播中的一组给定初始值的节点平均占比的演化曲线,r(t),b(t)和d(t)分别达到0.033 4,0.040 0和0.139 7,也跟谣言平衡点符合了E*。
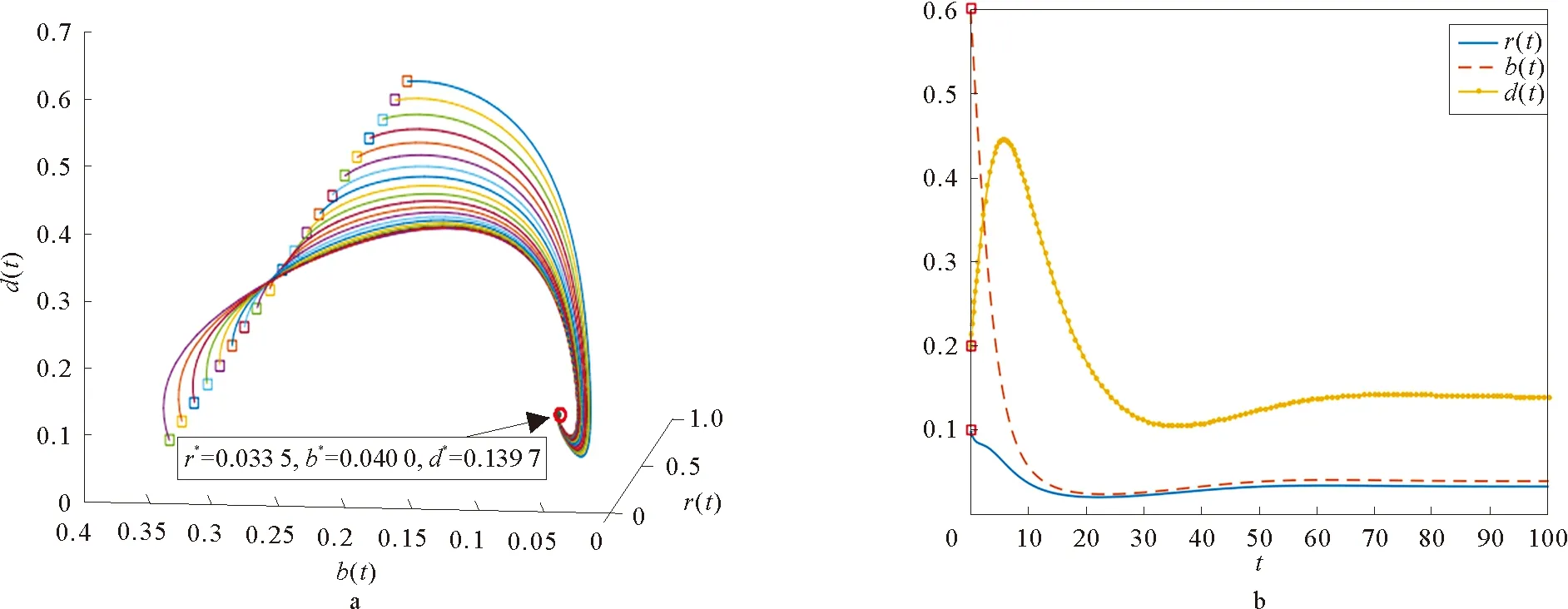
图5 谣言状态图Fig.5 Rumor state diagram
实验3为了模拟在线社交网络谣言的实际传播过程设计了仿真实验,实验采用离散时间的实验模型,搭建了一个3 000节点大小的小世界网络。根据研究表明在线社交网络具有许多小世界网络的特征特性。因此本文依据WS小世界模型来构造我们的实验网络。实验目的是验证本文提出的理论模型在实际网络中的效果。如图6a所示展示了实验生成的小世界网络结构,图6b展示了网络结构中的用户节点状态分布。
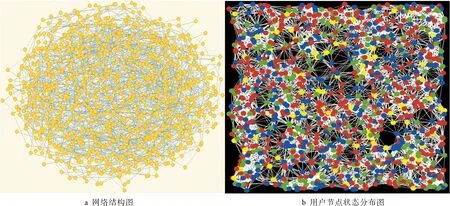
图6 网络结构图和用户节点状态分布图Fig.6 Network structure diagram and node state diagram
图7所示是实验1得到的结果与URBD模型的结果的对比图,其中蓝线显示的是URBD模型节点个数比例,红线显示的是实验网络传播谣言的节点个数比例。从图中可以看到在线社交网络谣言传播的走势与我们建立的URBD模型大体一致。
图8所示是实验2得到的结果与URBD模型的结果对比图。从图中可以看到在线社交网络谣言传播的走势与我们建立的URBD模型大体一致。
因在线社交网络的聚类系数较大,许多特征与小世界网络相似,实验3采用建立WS小世界网络进行在线社交网络谣言的传播,从实验结果看,文章建立的URBD模型由于考虑到网络谣言传播的中间状态且对谣言传播节点分类清晰,可以较为清晰地得到谣言传播的走势,且结果大致符合。
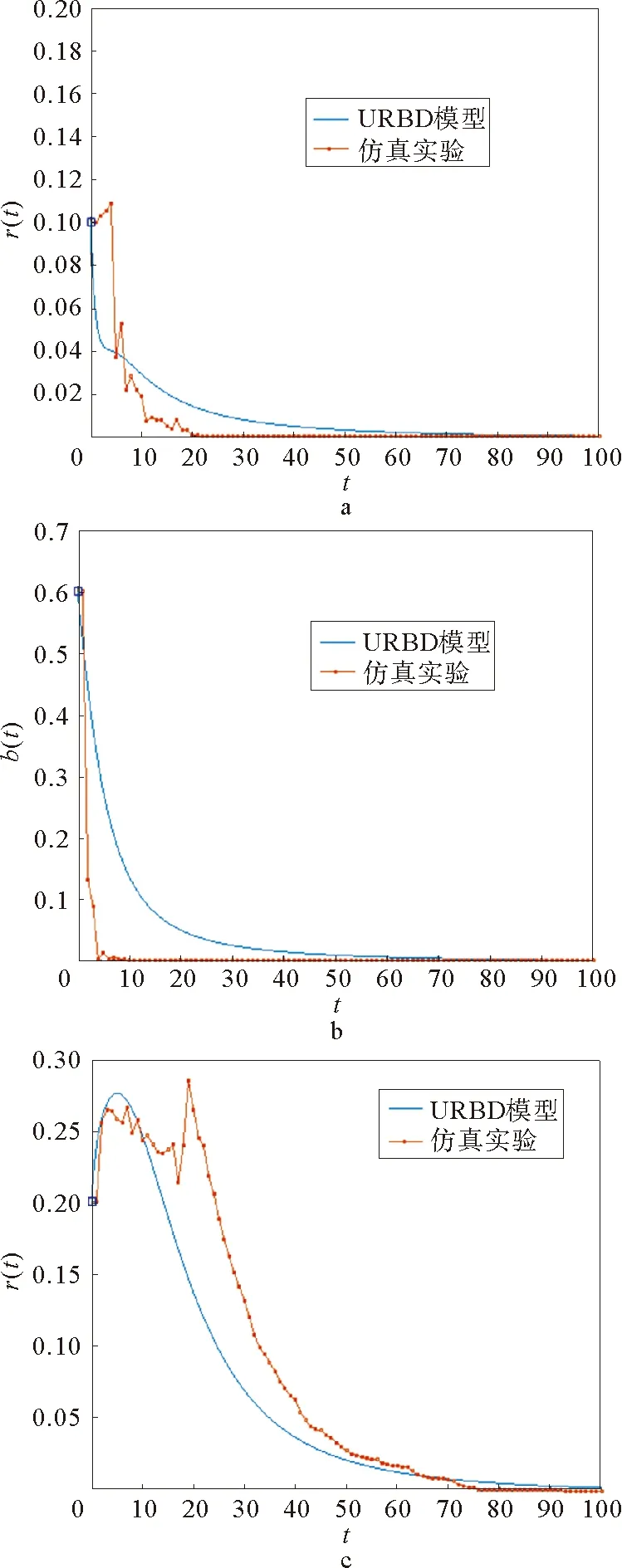
图7 URBD模型和实验网络传播谣言Fig.7 The URBD model and the spreading of rumor
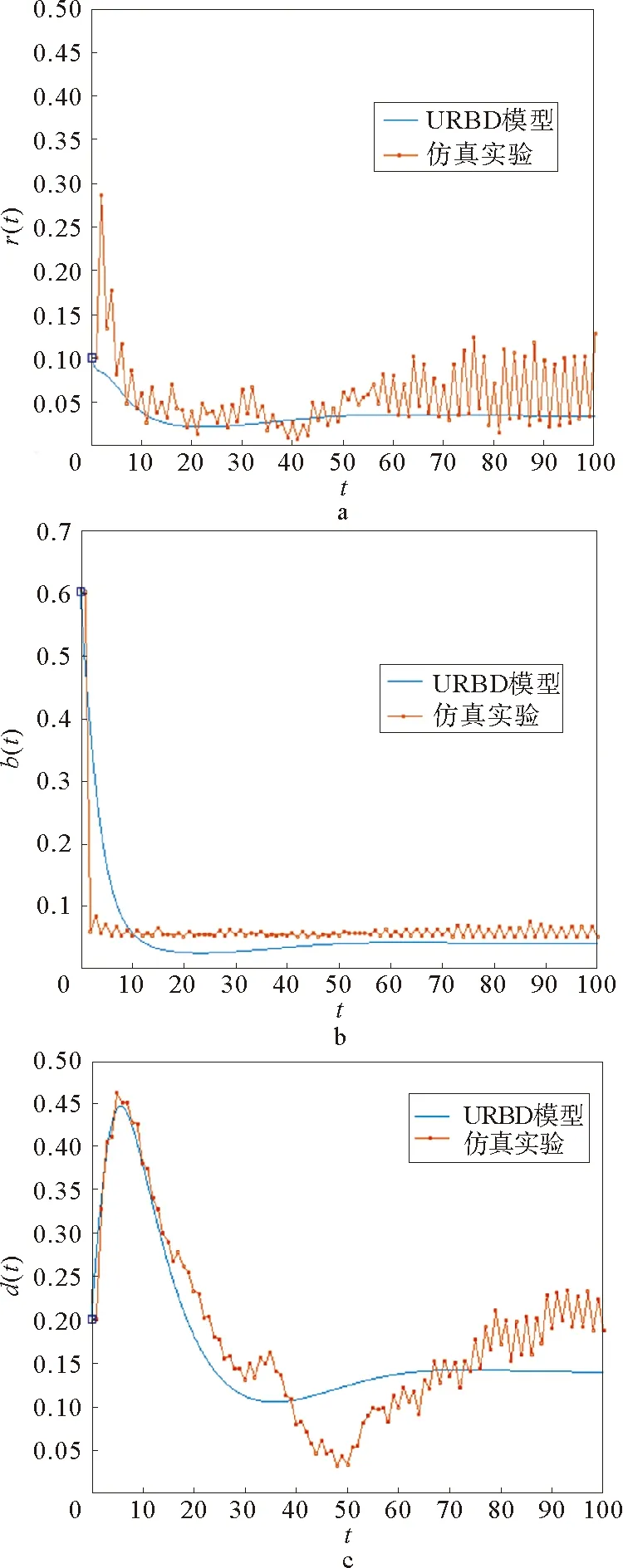
图8 URBD模型和实验网络传播谣言Fig.8 The URBD model and the spreading of rumor
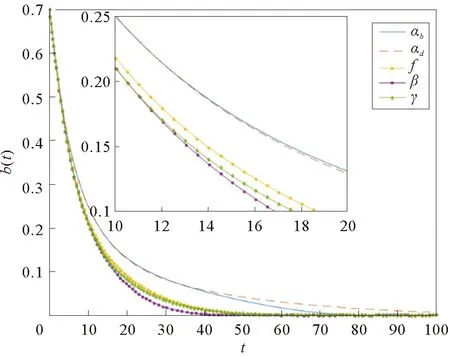
图9 传播影响效果随着αb和αd的变化Fig.9 Propagation effects vary with αb and αd
实验4在分析整个系统时,谣言传播阈值对于系统(4)是一个重要的决定性因素。因此,为了有效控制甚至防止网络谣言的传播,非常有必要采取一些措施来控制传播参数使得传播阈值R0小于1。在这部分,希望得到一些措施使得R0变小,达到控制网络谣言传播的目标。
分析所有模型的参数,我们发现参数f,β和γ可以直观地分析出对谣言传播模型的影响,如图9所示。分别对5个参数做正面处理,观察传播阈值的趋势。可以观察到αb和αd的对于传播阈值影响的效果并不是很明显。但我们不能从图中直观地看出参数αb和αd跟谣言传播的关系。
参数αb是用来表示R节点转化为B节点概率。于我们而言,显然分析参数αb跟R0之间的关系是十分必要的。观察参数αb关于R0的变化趋势,直接计算得到
可以看到参数αb的增加会导致传播阈值R0的增加,如图10所示。当参数αb很小的时候,传播阈值R0容易控制在1以下。因此我们考虑到αb是一个重要的因素可以比较容易地控制谣言使其趋于消失在谣言产生的初期。如图11所示,当我们减小参数αb,网络谣言可以耗费较短的时间去清除。
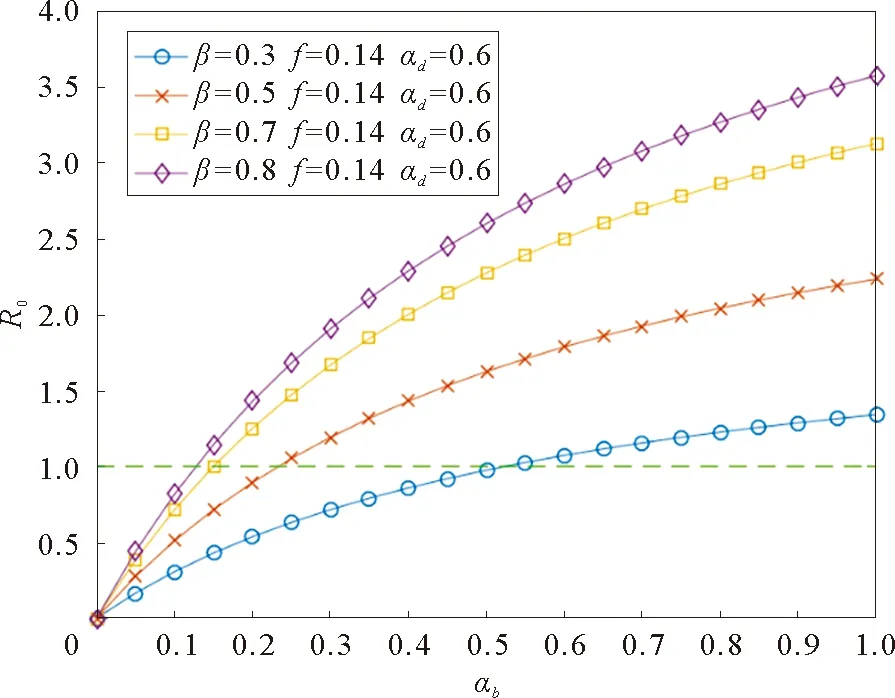
图10 传播阈值随αb的变化Fig.10 Propagation threshold changes with αb
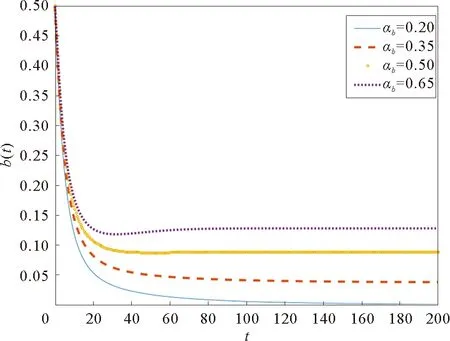
图11 b(t)随时间的变化Fig.11 Evolution of b(t)
为了更加全面地分析整个模型,我们同时考虑参数αd的变化对于系统的影响。与参数αb的分析类似,首先,得到参数αd和传播阈值R0的关系,如图12所示。同时观察随着参数αd的改变b(t)的变化趋势,如图13所示。
通过上述的数值分析,并不能直观得到对于传播阈值的影响。因此, 我们尝试通过付出相同的努力观察哪个参数对网络谣言传播的影响更为明显。
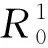
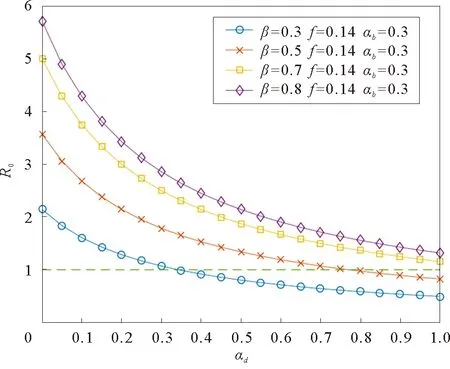
图12 传播阈值随αd的变化Fig.12 Propagation threshold changes with αd
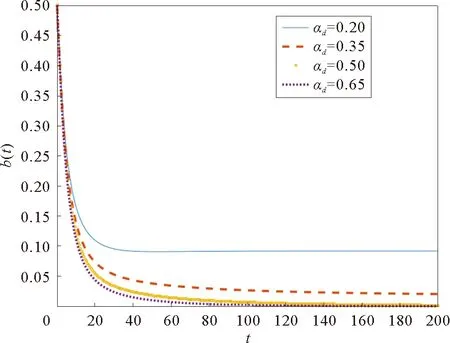
图13 b(t)的变化Fig.13 Evolution of b(t)
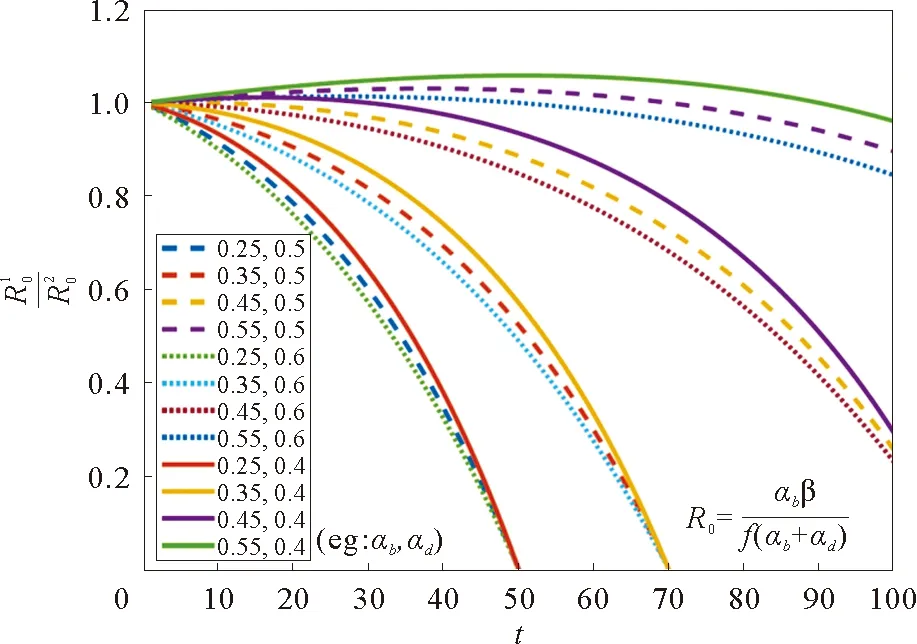
图14 参数αb和αdFig.14 Parameters αband αd
通过上述分析,得到一些有价值的结论,如下所示:
1)社交网络谣言传播初期,控制谣言传播的重要参数是αb。
2)当谣言已经存在一段时间,参数αb的大小变得尤为重要。假如参数αb还比较小,综合多方面因素的考虑需要提高参数αd的大小。假如参数αb已经非常大了,这时需要付出相同的精力同时控制参数αb和参数αd。
3)当谣言传播带来十分严重的后果时,应该同时考虑参数f、参数β以及参数γ。
4 结论
通过考虑用户遗忘率和文化程度以及社交网络的结构特点(消息缓存)建立一个全新的社交网络谣言传播模型。该模型与以前的模型有很大的区别,在于它提出一个新的状态节点,即R节点,得该模型可以更加符合现实社交网络谣言的传播。通过使用Lyapunov方法,得到谣言传播的平衡点。同样通过分析传播阈值R0,可以得到快速控制谣言传播的方法。
根据整篇文章对于谣言传播模型的研究与分析,可以得到一些控制社交网络谣言传播的建议。当谣言处于传播的初始阶段,需要减小参数αb,即提高用户的文化程度。短期快速提高文化程度可以通过权威媒体公开发表正确的消息来进行知识普及教育。同时通过各大社交媒体平台对已经识别到的网络谣言进行后台删除。当网络谣言传播一段时间后,应考虑参数αb的大小。如果只有较少一部分人相信谣言,可以先致力于提高从R节点到D节点的转换率,使得R节点尽快阅读到权威消息,通过加快权威消息的传播(如消息推送)。这样能够快速控制谣言的传播达到平息谣言的效果。当网络谣言传播比较严重时,即参数αb较大时,要考虑所有的方法来快速控制谣言传播避免造成更大的损失。
本文建立的社交网络谣言传播模型是基本模型,但是按照我们的想法,此模型可以考虑D节点转换为B节点的可能性,即多次听信谣言后用户对于谣言的态度会出现摇摆。R节点和U节点之间的转换也需要考虑得更加完善。同样对于社交媒体的传播途径也需要更加明确。沿着这个方向,我们下一步工作就是构造一个更加符合社交网络传播的网络谣言传播模型,为更好地发现网络谣言传播规律,控制网络谣言的传播而努力。
