多材料车身复杂装配顺序优化

李艳萍

(上海电机学院 机械学院， 上海 201306)

面向中国制造2025，个性化和小批量生产需求增加，制造变得日益复杂和多样化[1]。车身制造由单一钢材料车身向多材料车身转变，装配零部件材料增加，装配连接工艺、装配资源等也相应增加[2]。车身装配的多样化和不确定性为车身复杂装配带来新的特点[3-4]。装配顺序确定是装配系统设计规划和装配工艺实现的关键环节，装配顺序不仅决定本次装配操作的复杂性，同时决定了系统传递复杂性流动的方向，直接影响产品的可装配性、装配质量和成本[5]。基于复杂性分析的多材料车身装配顺序优化，发挥装配系统相关性信息传递复杂性的作用[6]，实现装配系统复杂性的优化配置。

本文在装配系统复杂性分析基础上，以传递复杂性为装配任务节点间成本阵列，描述多材料车身装配顺序优化问题，去除无效信息后的装配顺序优化，可类似于带约束的非对称旅行商问题(Asymetric Traveling Salesman Problem with Precedence Constraint, ATSP-PC)，建立节点间有效传递复杂性总和最小的装配顺序优化模型。随着装配节点数增多导致复杂性信息爆炸性增加，探索应用定向爬山遗传算法(Oriented Hill-Climbing based Genetic Algorithm，OHCGA)搜索得到问题求解。最后通过某型车身侧围装配实例验证，该方法有效降低了装配系统的复杂性，提高了装配系统的性能，并保证多材料车身装配的质量。

1 多材料车身装配顺序优化

1.1 车身装配系统

多材料车身装配顺序不仅决定了装配制造的过程，同时也决定了各装配工位间复杂性的有效传递与传播[5-7]。考虑包含多个车身零部件的装配，将每个车身零部件装配作为装配任务节点，用节点间有向顺序表示装配约束关系。假定如图1所示的9个节点分别对应车身零部件装配的子节点，其中，每一个任务节点用一个实线框表示，添加的虚拟节点“0” 用一个虚线圆圈表示，作为任务准备节点，向开始任务节点提供物料配送和工具准备，并且最终的装配也要回到该准备节点，以完成一个装配顺序和任务周期。令虚拟节点“0”的复杂性为零，且节点“0”到其他节点的装配复杂性，其他节点到节点“0”的装配复杂性均为零。基于复杂性分析的多材料车身装配顺序优化目标，就是寻找可行装配序列中具有最小系统复杂性的装配序列。

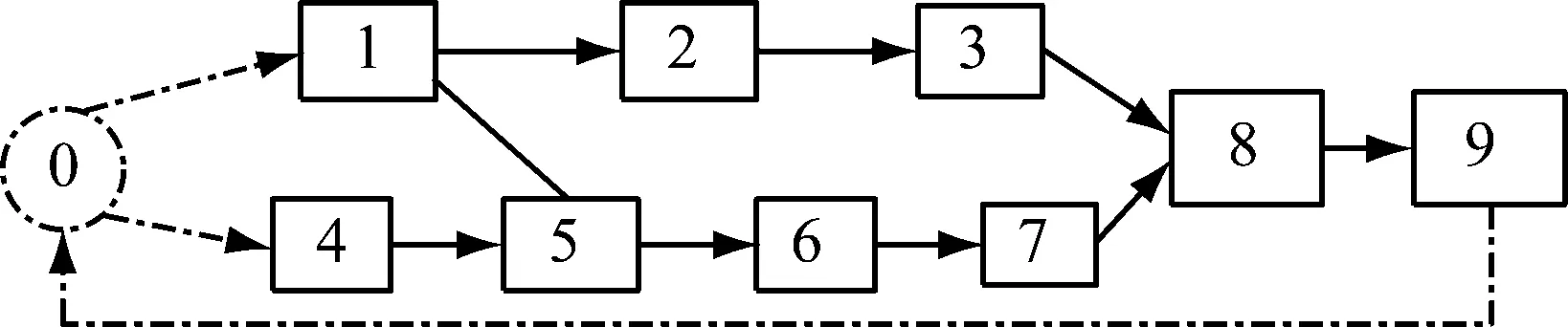
图1 九任务节点装配系统

1.2 装配节点复杂性度量

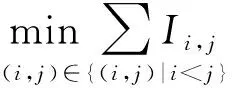
1.3 约简方案

多材料车身零部件繁多、装配结构复杂，存在n个装配节点的车身装配，若不考虑车身装配结构的优先级约束，则有n!个可行装配序列，直接求解一般比较困难。依据多材料车身装配操作复杂性的条件相关性，并考虑各装配任务节点间的互相关性，约简等价转换以利于问题的求解[5-7]。

本文依据车身结构及装配约束的优先级限制，识别装配序列中各任务节点间的不可行单元，将其标记为无效信息，清除它们以简化问题求解。

步骤1依据装配优先关系识别任务节点i优先于节点j的装配，并在装配复杂性成本阵列中标记。

步骤2检查装配复杂性成本阵列的第i行，若其第j列未标记，则表明i和j互不相关，任务i既可安排在任务j前，也可在其后被装配，对应的装配节点间复杂性为Ii，j(节点i先于节点j装配)或为Ij,i(节点j先于节点i装配)。

步骤3所有未标记的单元为不许可单元，标记为∞。

上述过程隐含了一种简化复杂性成本阵列而不改变问题解的方法，可设置步骤1标记的单元为零，其对原始问题的唯一改变可通过设置一个常数来反映，而不改变问题的求解。表1为简化的复杂性成本阵列。

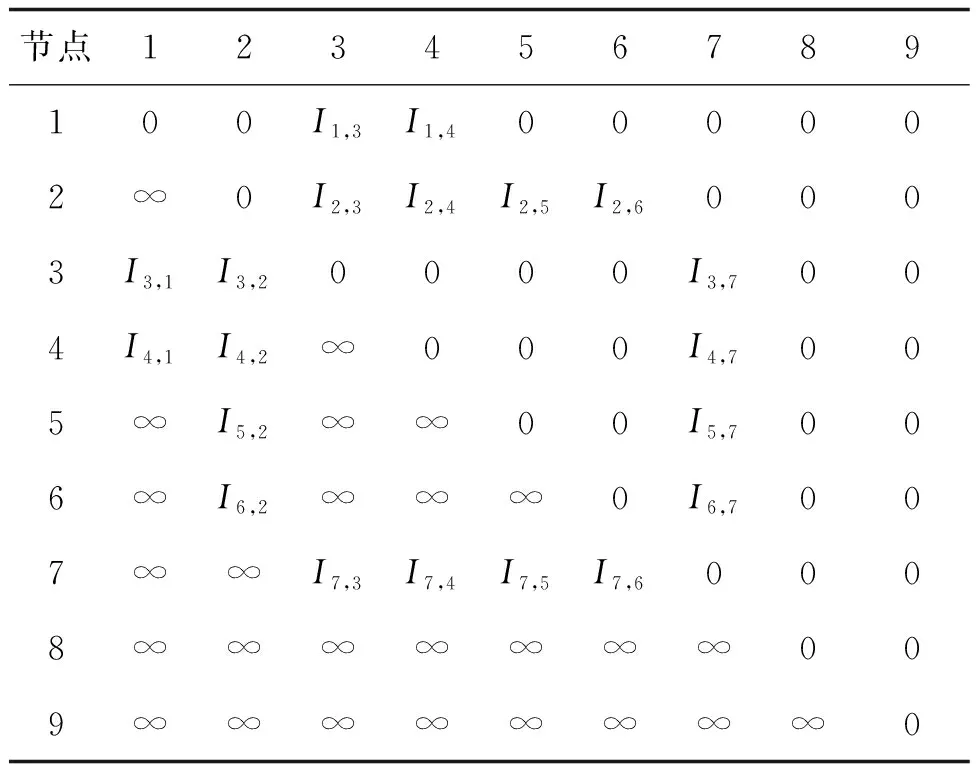
表1 简化的复杂性成本阵列

由于多材料车身装配操作非独立相关条件信息熵的存在，节点间装配操作复杂性与顺序和方向均相关，即，一般情况下Ii,j≠Ij,i。由此，多材料车身装配顺序优化问题可类比于ATSP-PC[8-10]。

2 装配顺序优化模型

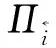
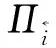
多材料车身装配顺序优化问题的目标函数，为由节点i开始的顺序路径决定的有效复杂性成本和最小。从装配节点i出发，合理地访问集合N-S中的节点(n+1-|S|)，并最终返回到虚拟节点“0”结束，然后访问从状态(S,i)到状态(S∪{j},j)发生状态转移的节点j(j∈D(S)，D(S)为由状态(S,i)后有可能被访问的点集组成的决策空间)。建立基于复杂性分析的多材料车身装配顺序优化模型，以最小化装配复杂性总和为优化目标函数，同时装配顺序优化还受节点流动方向和任务节点复杂性约束，即

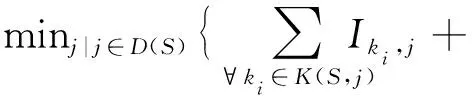
f(S∪{j},j)

s.t. (i) {0}⊆S⊂N,i∈S

S=N，i∈S{0}

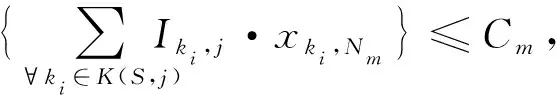
m=1，2，…,M

(1)

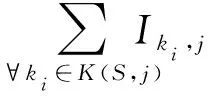
3 OHCGA算法求解

多材料车身装配顺序优化问题，随着装配节点增多，装配序列急剧增多，计算复杂性也将随着节点数的增多而爆炸式增加，需探索一种有效的方法求解问题。遗传算法[11]模拟了自然选择和生物进化过程中的繁殖、交叉和变异现象，使适应度高的个体基因在下一代种群中占有更高比例，通过自组织、自适应、自学习的群体进化，引导搜索向全局最优解收敛。但由于其存在早熟现象使算法搜索很快收敛到局部最优解而不是全局最优解。爬山法[12]为一种局部搜索机制，从解空间的任意位置开始，快速收敛于局部最优解，对求解单峰问题具有显著效果。本文在遗传算法基础上引用OHCO，在每一代进化操作中，定向地在产生优秀个体的方向上生成更优秀的个体取代当前个体，引导算法有效地向全局最优解收敛，改善算法搜索全局最优解的能力[13]。实现过程如图2所示。

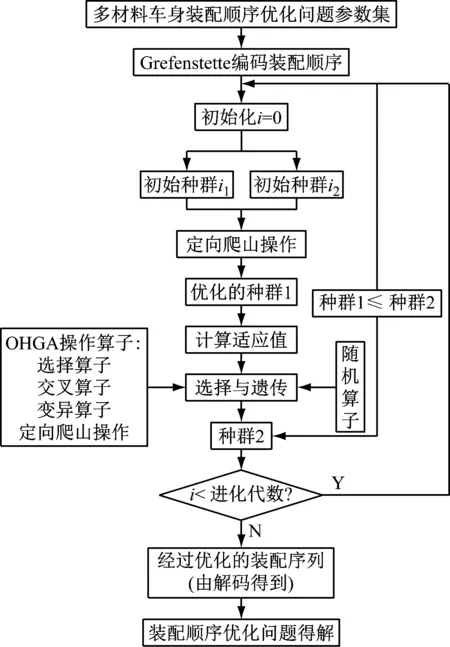
图2 OHCGA算法求解流程

OHCGA算法求解[13]。采用基于顺序表示的遗传基因Grefenstette编码[14-15]。算法求解的适应度函数，为目标函数和各约束条件惩罚函数的

和[15]，即

F(C)=O(C)+P(C)+G(C)

(2)

式中:O(C)为装配顺序优化的目标函数；P(C)为各装配节点超出约束条件的惩罚函数；G(C)为超出装配人员可承受装配操作复杂性的惩罚函数。

4 应用实例

以某型多材料车身侧围为例，进行基于复杂性分析的装配顺序优化，图3所示为该车身侧围零部件装配模型。

图3 某型车身侧围装配模型

依据车身侧围装配关系，推导出侧围装配的优先级：外板基础上装配内板，然后装配加强板、隔板，并依此建立侧围的装配模型。可行装配序列流向如图4所示。对于装配节点2～9区域，由装配关系表示复杂性信息列表，依据装配约束清除无效信息，得到任务间传递复杂性成本阵列。

多材料车身侧围装配，其中，零部件选择为工位装配操作的首要任务，主要由本工位装配操作信息决定，装配夹具选择为满足本工位零部件的装配要求，均为“进给复杂性”；而装配工艺、设备、工具及装配顺序选择，需考虑受其上流工位影响的“传递复杂性”。因此，车身侧围装配顺序优化，需分析度量装配工艺、设备和工具等的选择复杂性和装配顺序选择复杂性。车身侧围装配任务节点间的传递复杂性计算，如节点2(后大灯支座)对节点8(B柱内板总成)，节点8可供选择的材料主要包括普通碳素钢、高强度钢、铝合金和复合材料，由各类材料的零部件选择概率，对应不同车身材料，主要存在点焊、自冲铆、胶接与胶铆复合4种连接工艺。则装配工艺选择条件熵复杂性为

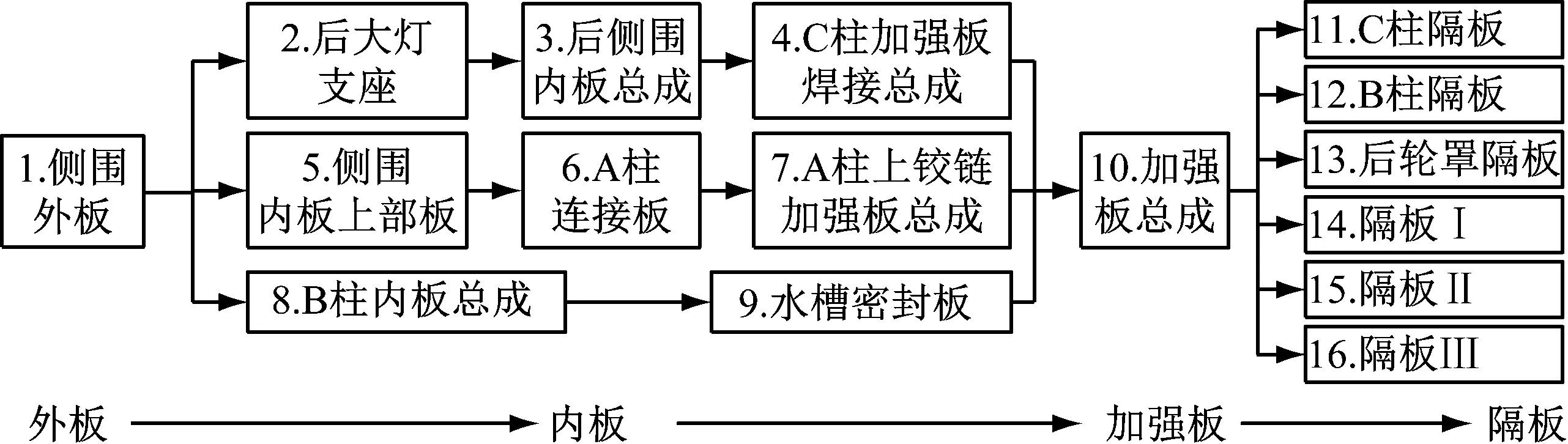
图4车身侧围装配顺序流向示意图

(3)

式中：p(xk2,xk1)为零件选择和工艺选择的联合概率；p(xk2|xk1)为不同工艺对应零部件材料的条件选择概率。各装配操作条件选择传递复杂性可由式(3)类似计算。考虑各选择复杂性的权重，由下式可得多材料车身侧围装配节点2对节点8的传递复杂性公式：

(4)

式中：Hku为第ku类装配操作的条件信息熵复杂性。αku为第ku(ku=k1,k2,…,K)类装配操作的作用系数，若包含第ku类装配操作，则令αku=1，否则αku=0。wku为第ku类装配操作的权重，基于数据分析和粗糙集客观评价，并结合专家知识综合确定多材料车身装配各操作复杂性权重[16]为

[wk1wk2wk3wk4wk5]-1=

[w零件w工艺w设备&工具w夹具w顺序]-1=

[0.2160.231 0.114 0.126 0.313]-1

同理可得其他各装配节点的有效传递复杂性度量。考虑到计算方法的相似性和计算数据量繁多，用Matlab实现各节点有效传递复杂性的计算。车身侧围装配2～9各节点间的传递复杂性见表2。

2～9的8个装配任务节点，经装配约束分解后的可行装配序列统计有560种，应用OHCGA启发式搜索求解，Windows系统下，Matlab 程序实现了OHCGA对该问题的求解[17]。经多次求解发现，当遗传代数N在100左右时可趋于稳定，为求解稳妥，取遗传代数N=200。OHCGA搜索寻优，进化代数N=200的进化过程如图5所示。

求解得到传递复杂性最小的装配顺序，经Grefenstette反编码解码后为：5→6→2→3→4→7→8→9，对应的最小复杂性为20.99 bit。而依据装配模型和装配约束关系产生的可行装配序列中，互信息熵表示的传递复杂性最大为35.83 bit，最优装配顺序的传递复杂性低于最大传递复杂性，相对减少41.42%，可见该方法减少车身装配系统复杂性的效果显著。同理可得11～16节点的装配顺序优化，对应复杂性最小的装配顺序为：12→11→13→15→16→14。综上，该侧围装配操作复杂性最小的装配顺序为：1→5→6→2→3→4→7→8→9→10→12→11→13→15→16→14。

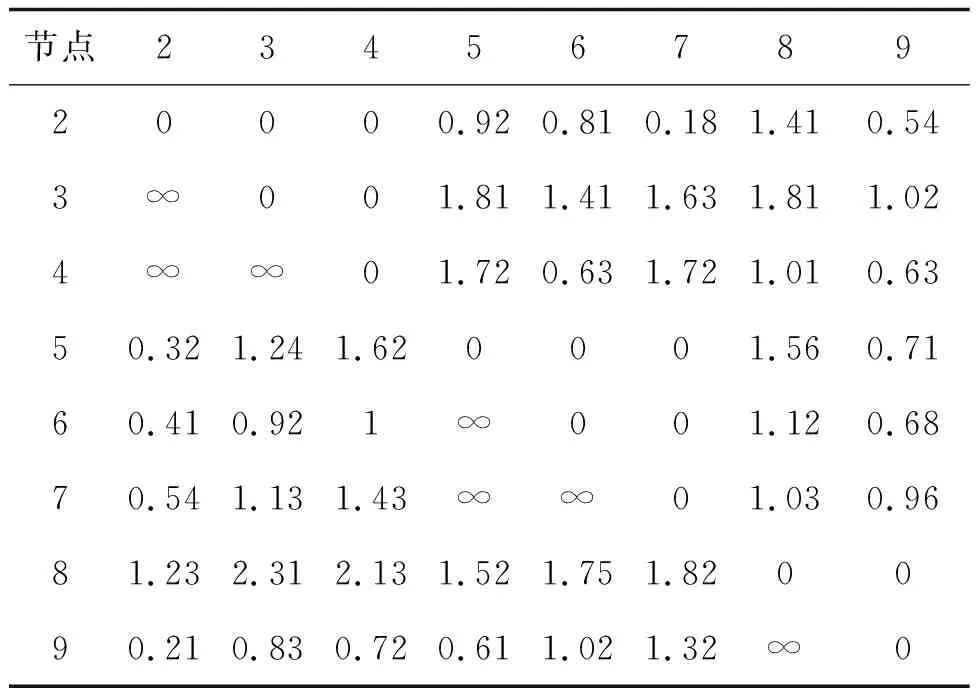
表2 节点2～9中各节点间传递复杂性

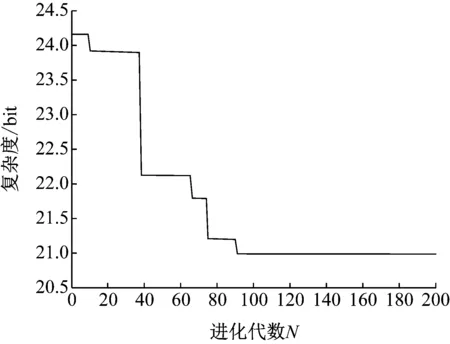
图5 爬山遗传算法寻优过程(N=200)

5 结 论

本文多材料车身装配顺序优化，基于传递复杂性与装配顺序的相关性，将多材料车身装配顺序优化问题类似于具有顺序约束的ATSP-PC，并建立有效传递复杂性总和最小的装配顺序优化模型。多材料车身复杂装配顺序优化问题随着装配节点数的增多，其求解的信息量产生爆炸性增加而使问题的求解难度增加，应用OHCGA启发式搜索得到装配顺序优化问题的求解。最后通过车身侧围复杂装配实例验证了方法的可行性和有效性，合理装配顺序优化的同时有效降低了车身装配系统的复杂性，并使装配系统性能得以优化。