Archimedean Copula函数在风电场功率爬坡风险评估领域中的应用
2018-12-29程亚丽王致杰江秀臣
程亚丽, 王致杰, 江秀臣
(1. 上海电机学院 电气学院,上海 201306; 2. 上海交通大学 电气工程学院,上海 200240)
目前,对功率爬坡事件的研究主要集中于爬坡预测上[1],而爬坡事件对电网产生的风险的研究很少,且只是对爬坡单一特征量进行分析[2],已经很难满足对于极端气候变化特征和电网风险管理的需求。因此,有必要对爬坡要素间的相互关系和联合概率分布特征进行研究。Sklar[3]在1959年提出的Archimedean Copula函数,是一类将变量联合分布函数与边缘分布函数连接在一起的函数,很好地描述变量之间的相关性并计算其联合概率分布。联合分布里包含了所有风险要素的信息,可以全面评估事件的风险大小,被广泛地用于水文事件、干旱、沙尘暴等方面的多变量研究中[4-10]。文献[11-13]把Copula理论运用到了金融市场的风险分析中,分析风险因子之间的相关性;文献[14-16]结合Copula理论对投资组合风险进行度量,能够更准确地度量投资组合的风险值。但是将此函数运用在风电场功率爬坡风险评估方面较少,本文利用Archimedean Copula函数多维联合的灵活性,构建风电功率爬坡事件的二维联合分布,建立了莱州风电场发生功率爬坡的概率模型,定量分析风电场发生功率爬坡的风险,为风电场功率爬坡风险评估研究提供新的思路。
1 风电场功率爬坡特征量的选取
在短时间内风电功率的剧烈波动使得风力发电具有不确定性、间断性和随机性,这种现象被称为风电功率爬坡事件,描述一个爬坡事件的主要特征量是确定的,包括爬坡幅值、爬坡方向、爬坡率、爬坡起止时间和持续时间,如图1所示。爬坡幅值通常是在爬坡持续时间内最大和最小功率的差值,爬坡方向用爬坡幅值的正负表示,正代表上爬坡事件,负代表下爬坡事件。

图1 爬坡事件特征图
由图1可见,爬坡幅值越大,爬坡持续时间越短,则爬坡事件越严重。因此,选取爬坡幅值和爬坡持续时间这两个特征量作为风电功率爬坡事件的主要特征量,建立二维联合分布。
2 Archimedean Copula函数
Archimedean Copula函数主要包括Frank Copula、Clayton Copula和Gumbel Copula函数,本文选用3种二维Archimedean Copula函数进行爬坡特征量二维联合,具体的分布函数及参数范围如表1所示。
对于Archimedean Copula函数拟合度的检验方法通常采用离差平方和(Oridinary Least Square,OLS)准则法,采用文献[5]中的OLS准则法公式。该函数参数拟合度优劣的判断依据是OLS越小,表明该Archimedean Copula与其经验点距的误差越小,函数拟合程度越好。

表1 二维Archimedean Copula分布函数及参数范围
表1中,u1,u2为Archimedean Copula函数中的两个随机变量。
3 基于Archimedean Copula函数的爬坡特征量联合分布
3.1 爬坡特征量边缘分布函数
通过对目前国内外概率分布函数的研究,本文假定爬坡持续时间服从对数正态分布,风电功率爬坡幅值服从广义极值分布,则相应的分布函数和概率密度函数设计如下:
设随机变量x的样本点为x1,x2,…,xn,随机变量指的是风电功率爬坡持续时间的实际数据,对数正态分布的概率密度函数为
(1)
风电功率爬坡持续时间t的累积分布函数为
(2)
式中:μ为随机变量的均值,也称为位置参数;σ2为标准差,也称为形状参数。
极值分布是指在概率论中极大值(或者极小值)的概率分布,概率密度函数为

(3)
爬坡幅值ΔP的累积分布函数为
(4)
式中,α为尺度参数。
利用极大似然函数进行边缘分布参数估计,爬坡持续时间的参数估计计算公式如下:
(5)
对式(5)两边取对数,得
(6)
根据式(6)建立似然函数组为
(7)
可得
式中:L(μ,σ2)为似然函数;ti为爬坡持续时间变量。爬坡幅值分布函数的参数估计按照式(5)~式(7)类推。
4 实例研究
本章算例采用的数据是2015年一年莱州风电场的实测数据,风力发电机组的输出功率每15 min采样一次,分别采用对数正态分布、广义极值分布对爬坡持续时间和爬坡幅值进行拟合,利用极大似然法对各边缘分布函数进行参数估计,并通过K-S法对各边缘分布函数进行检验。采用Archimedean Copula函数构建风电功率爬坡幅值和爬坡持续时间的联合概率分布模型,并根据OLS准则法最小原则,选取最合适的Archimedean Copula函数构建爬坡幅值和爬坡持续时间的联合概率分布函数。
4.1 爬坡特征量拟合分布
运用极大似然法分别对爬坡持续时间、幅值的边缘分布函数参数进行估计,结果如表2所示。利用K-S法对各分布函数进行检验,取K-S检验的显著性水平α=0.05,当n=44时,查询检验分位数表得到对应的分位点D0=0.200 56,当边缘分布的检验统计量D<0.200 56时,表明K-S检验通过且拟合情况较好。爬坡幅值、持续时间的K-S检验的计算结果如表3所示,对数正态分布和广义极值分布对于爬坡特征量的拟合检验值都通过了0.05的显著性检验,说明上述两种概率分布函数对于爬坡特征量的拟合效果较好。因此,选取广义极值分布进行爬坡幅值边缘分布的拟合,选取对数正态分布进行爬坡持续时间边缘分布的拟合。
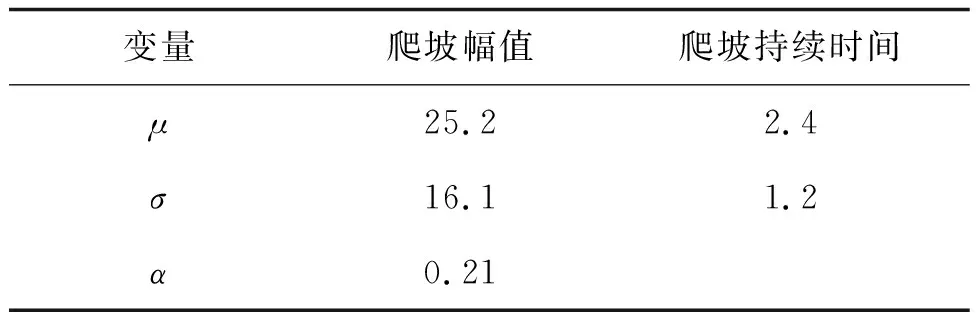
表2 边缘分布函数的参数值
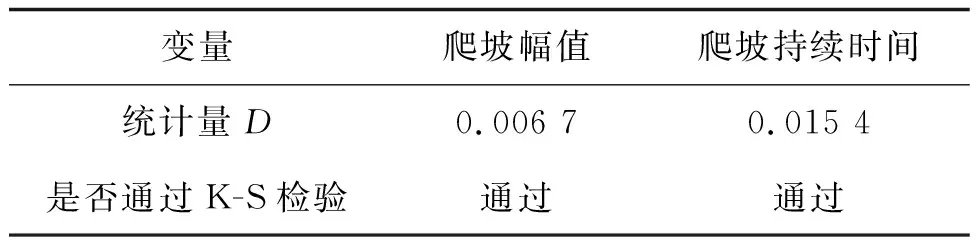
表3 爬坡特征变量的K-S检验
4.2 爬坡特征量二维联合分布
对爬坡特征量中的爬坡持续时间和爬坡幅值构建Archimedean Copula函数二维联合分布,利用式(5) ~式(7) 进行参数估计,采用表1中的函数公式进行二维拟合,通过OLS准则法进行优度检验,相关参数及检验值见表4。

表4 分布函数参数及检验值
从表4中可见,从K-S检验统计量D值分析,3种Archimedean Copula联合函数的D值都小于临界值0.200 56。因此,3种函数都可以构建莱州风电场爬坡持续时间与爬坡幅值的联合分布模型;从拟合优度的评价指标分析,Clayton Copula函数构建的联合分布模型的OLS值最小,拟合效果最优。因此,选取Clayton Copula函数模型为莱州风电场爬坡持续时间与爬坡幅值的联合分布模型。
为了进一步验证拟合效果的优劣,利用Matlab软件对莱州风电场爬坡持续时间与爬坡幅值的数据编程,Frank Copula函数可以很好地描述对称的相关关系,以Frank Copula函数为例,运用Matlab求Frank Copula函数参数程序如下。
⋮
调用copulafit函数估计二元Frank Copula中的参数
rho_norm = copulafit('Frank',[U(:), V(:)])
[Udata,Vdata] = meshgrid(linspace(0,1,31));
Cpdf_norm = copulapdf('Frank',[Udata(:), Vdata(:)],rho_norm);
Ccdf_t = copulacdf('t',[Udata(:), Vdata(:)],rho_t,nuhat);
绘制二元Frank Copula的密度函数图
figure;
surf(Udata,Vdata,reshape(Cpdf_norm,size(Udata)));
xlabel('爬坡持续时间');
ylabel('爬坡幅值');
zlabel('二元Frank Copula密度函数)');
⋮
通过Matlab仿真,得到爬坡持续时间与爬坡幅值的概率密度分布图如图2~4所示。Frank Copula函数具有对称性,尾部很厚,可用于描述具有对称的相关关系(见图2)。由于风电场发生严重爬坡事件和一般爬坡事件时不具有对称性,因此该函数不能很好地描述风电场功率爬坡严重事件引起的风险。Gumbel Copula函数分布似“J”形,拥有较厚的上尾部特征,上尾部特征是描述变量间同时出现大的变化的概率(见图3)。风电功率爬坡特征量的Gumbel Copula函数上尾部特征突出,不能很好地描述风电场中爬坡幅值较大且爬坡持续时间较短的极端爬坡事件。Clayton Copula不具有对称性,分布似“L”形,具有较厚的下尾部特征(见图4)。风电功率爬坡特征量的Clayton Copula函数具有很好的下尾部特征,能较好地描述极端爬坡事件小概率发生的现象,从而可以分析极端事件引起的损失。

图2 Frank Copula函数的爬坡幅值和爬坡持续时间概率密度分布
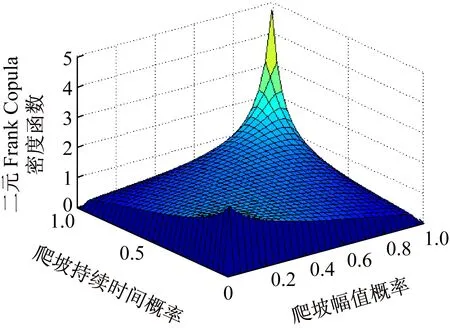
图3 Gumbel Copula函数的爬坡幅值和爬坡持续时间累计概率分布

图4 Clayton Copula函数的爬坡幅值和爬坡持续时间概率密度分布
根据上述分析可知,可用Clayton Copula函数描述莱州风电场功率爬坡幅值和爬坡持续时间的联合分布,表达式如下:
FΔP,t=Cu1,u2=
(8)
莱州风电场功率爬坡幅值和爬坡持续时间的联合分布概率计算模型如下:
F(ΔP1≪ ΔP≪ ΔP2,t1≪t≪t2)=
F(ΔP2t2)-F(ΔP2,t1)-F(ΔP1,t2)+
F(ΔP1,t1)
(9)
该模型同时包含了爬坡幅值和爬坡持续时间信息,可准确地计算爬坡事件发生的概率,能定量分析风电功率爬坡事件的风险评估,方便调度人员更好地做出调度策略,减少风险引起的损失。
5 结 语
选取了风电功率爬坡事件的爬坡持续时间和爬坡幅值两个特征量,对其采用对数正态分布和广义极值分布进行边缘分布拟合,并在建立风电功率爬坡幅值和爬坡持续时间边缘分布模型中,推导了利用极大似然法进行参数估计的过程,最后采用K-S检验法对拟合优度检验。在此基础上,根据3种Archimedean Copula函数模型的表达式建立了爬坡幅值和爬坡持续时间的二维联合分布函数,并采用OLS准则法作为拟合优度的评价指标,确定了Clayton Copula模型作为莱州风电场爬坡事件概率计算模型,从而定量地分析风电场功率爬坡的风险。本文为风电场功率爬坡风险评估方面提供一定的理论依据和支撑,拓展了Copula理论的应用前景。
