泡沫陶瓷吸热体结构参数对吸热器性能的影响
2018-12-29李青,徐宏
李 青, 徐 宏
(上海电机学院 电气学院,上海 201306)
在众多的太阳能利用技术中,太阳能热发电技术(Solar Thermal Power, STP)是一种将太阳辐射能聚集起来加热传热流体,再通过热-工转换过程进行发电的技术[1-3]。STP在众多的新能源发电技术中占据着重要席位,且具有作为未来电力系统基础负荷的潜力[4]。根据国际能源署的预测,到2050年全球太阳能热发电装机容量将达到1 089 GW,占全球电力总需求的11%[5]。
基于吸热器传热流体的不同,塔式STP主要分为水/水蒸汽、熔融盐、空气3大类[6-8]。以空气作为传热流体具有成本低廉、无污染、无相变、工作温度高、无需预热、适合缺水地区等优点。
空气吸热器作为空气式太阳能热发电系统中的核心部件,发挥着类似传统火力发电站中锅炉的重要作用,目前空气吸热器多以容积式为主,其吸热体大部分采用多孔材料。太阳辐射可从吸热体表面穿入多孔结构内部,空气在动力驱动下沿辐射入射的相同方向流经吸热体并与吸热体材料进行对流换热。容积式吸热器固体材料温度最高点通常位于吸热体内部,而非吸热体表面。因此,相比之前的管式吸热器,容积式吸热器在允许更高入射太阳辐射能流密度的同时很大程度减少了吸热器前表面热量损失[9]。
按照研究开发的先后顺序,容积式空气吸热器主要可分为金属丝网、吸热管式、模块式蜂窝陶瓷、颗粒型等空气吸热器[10]。空气吸热器的工作条件要求其吸热体材料具有导热系数大、强度高热膨胀系数低、抗热冲击能力强并且抗高温氧化等特性。碳化硅泡沫陶瓷是近年来被认为最具发展潜力的太阳能空气吸热器的吸热体材料。
泡沫陶瓷吸热体的3个结构参数分别为孔隙率、平均孔径和吸热体厚度。其中,吸热体厚度对吸热器压损的影响规律较为简单,即厚度越厚压损越大。相比而言,孔隙率和平均孔径对空气流经吸热体的压损影响规律较为复杂,且孔隙率和平均孔径对于吸热器温度分布的影响居于主导地位[11]。因此,诸多研究者针对该两个结构参数对泡沫陶瓷空气吸热器展开了研究[12-15]。本文采用数值模拟方法研究孔隙率和平均孔径对泡沫陶瓷容积式空气吸热器性能的影响规律,分析结果对该类吸热体结构的优化设计起到理论指导作用。
1 传热模型建立
空气吸热器是以空气为传热流体的塔式太阳能热发电系统中的最关键部分,而吸热体是空气吸热器最核心的部件,通常为多孔材料。空气吸热器的工作原理为:吸热体吸收聚光太阳辐射并把其转化为热能,空气在压力的驱动下流经吸热体,通过与多孔材料吸热体的固体骨架表面进行强制对流换热而温度升高,最后获得高温的出口空气。本文所研究的吸热体为图1所示碳化硅泡沫陶瓷吸热体,其结构为直径200 mm、厚度50 mm的圆柱体。

图1 碳化硅蜂窝陶瓷吸热体
空气吸热器保温层的保温效果良好,从吸热体侧圆周面向外界的对流和辐射热损失忽略不计,对吸热器的研究主要是对其中吸热体的研究。本文基于CFD软件,针对图1中圆柱形碳化硅泡沫陶瓷吸热体建立了二维稳态仿真模型。为将实际的三维实体进行合理简化,作如下假设:
(1) 聚光后的太阳能辐射在空气吸热器表面为均匀分布;
(2) 泡沫陶瓷吸热体材料为各向同性;
(3) 吸热体固体的热物性参数不随自身温度的变化而变化。
1.1 模型控制方程
多孔介质具有高度不规则的微观结构,因此研究者们多从宏观角度出发对其进行建模。按照是否考虑吸热体内气固两相的温差,宏观尺度上的数值模型又可分为局部热平衡(Local Thermal Equilibrium, LTE)和局部非热平衡(Local Thermal Non-Equilibrium, LTNE) 两种。前者基于流、固两相高强度换热假设,不考虑流体与固体骨架之间的换热温差,气固两相的能量方程被整合为一个综合的能量传递方程,故又称作一方程模型。后者考虑了气固两相间的温差,分别建立固体和气体相的能量传递方程,并通过容积换热系数将两者耦合起来,又被称作两方程模型。LTNE相比LTE需多求解一个能量控制方程,相对复杂,本文选取了LTE方程模型多泡沫陶瓷吸热器进行建模。
稳态能量方程为
(1)
式中:ρ为密度,kg/m3;Cp为定压比热容,J/(kg·K);下标f为流体;uD为空气的表观流速,m/s;T为温度,K;keff为泡沫陶瓷多孔介质的等效导热系数,W/(m·K);qr为辐射传热热流密度,W/m3;I为吸热体内部太阳辐射体积热流密度,W/m3。
稳态动量方程为
(2)
式中:ε为泡沫陶瓷的孔隙率;p为空气压强,Pa;μf为空气黏度,kg/(m·s);u′为空气的真实流速,m/s;x为沿空气流动方向距离吸热器入口的距离,m;Δp/x为由于多孔介质的存在导致的压力损失,Pa/m;该压力损失将会在下文详细介绍。
1.2 热传导模型
泡沫陶瓷吸热器内部的热传导包括固体间与流体间的热传导。由于泡沫陶瓷结构复杂,研究者多采用等效导热率来处理其内部的热传导过程。该系数keff由固体和流体的导热率按照体积平均计算得出[13]:
keff=εkf+(1-ε)ks
(3)
式中:kf为流体相导热率,W/(m·K);ks为固体相导热率,W/(m·K)。
1.3 辐射模型
空气吸热器工作时其温度可高达1 000 °C,因此,多孔材料固体间的热辐射对传热的贡献不可忽略[16]。针对多孔吸热体数值模拟,常用的两种处理固体间辐射换热的方法为Rosseland和P1模型近似,其中Rosseland模型更适用于光学厚度厚的多孔介质[17-18]。
泡沫陶瓷为光学厚度厚的介质,其光子的平均自由程相对于所研究求解域的尺寸来说很短,辐射强度通常只受到附近区域内固体发射辐射的影响。这种情况下,光子的运动可以类比为分子在介质中的扩散。本文选择使用Rosseland辐射模型,将全漫反射和漫散射下的泡沫陶瓷固体间辐射传输方程按照近似于傅立叶热传导定律的方法进行处理,辐射热流密度可表述为
(4)
式中:σ为斯蒂芬玻尔兹曼常数,W/(m2·K4);α为多孔介质固体材料的吸收系数,1/m;δ为多孔介质固体材料的散射系数,1/m。
1.4 压损模型
本文使用多孔介质中经典的Darcye-Forchheimer压损方程,计算吸热体内的压强分布[11],即
(5)
式中:μf为流体的速度;K1和K2分别为多孔吸热体材料的渗透系数和惯性系数。
Ergun等[19]推导得出K1和K2与多孔材料特征长度和孔隙率之间的关系式,即:
(6)
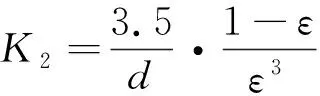
(7)
式中,d为泡沫陶瓷的平均孔径,m。Ergun公式在研究多孔介质中流体压损中得到了广泛应用,同样也被用于多孔容积式空气吸热器的建模中[11-15]。
1.5 体积热源
由于泡沫陶瓷吸热体的多孔结构特性,太阳辐射可部分穿透吸热体表面进入吸热体内部,本文选用体积热源的方式将太阳辐射能流密度加入模型中,该体积热源在吸热体内部的空间分布可由下式计算得[13]
(8)
式中:Fpeak为入射到吸热体表面太阳辐射能流密度的峰值,W/m2,本文中取作1 MW/m2;σ为投入辐射高斯分布的椭圆度,m,文中取作72.4 mm;λ为吸热体材料的吸收率, 根据泡沫陶瓷物性参数,本文取作0.8;β为消光系数,1/m,该值可根据泡沫陶瓷的平均孔径取倒数求出,即β=0.56/d[20]。
1.6 边界条件
模型中将入口边界压强设置为标准大气压(101 325 Pa),入口空气温度设置为300 K, 入口空气质量流量为0.05 kg/s。由于模型假设吸热器保温良好,因此,吸热体外围边界设置为绝热边界。
1.7 物性参数
由于空气吸热器工作温度范围广,因此本模型中考虑了空气的变物性,将空气各个物性参数表述成与空气温度相关的关系式。
空气密度为
(9)
空气比热容为
(10)
空气热导率为
(11)
空气黏度为
(12)
由于吸热体固体材料物性参数随温度的变化较小,故在模型中将固体的物性参数设置为常数,如表1所示。

表1 泡沫陶瓷固体物性参数表
1.8 网格划分
鉴于吸热体的圆柱形对称结构,只针对1/2圆柱剖面进行模型求解,其网格划分如图2所示。由图可见,求解区域包含了吸热体和吸热体后端管道两个部分,划分网格时对各求解区域的边界进行了网格加密处理。
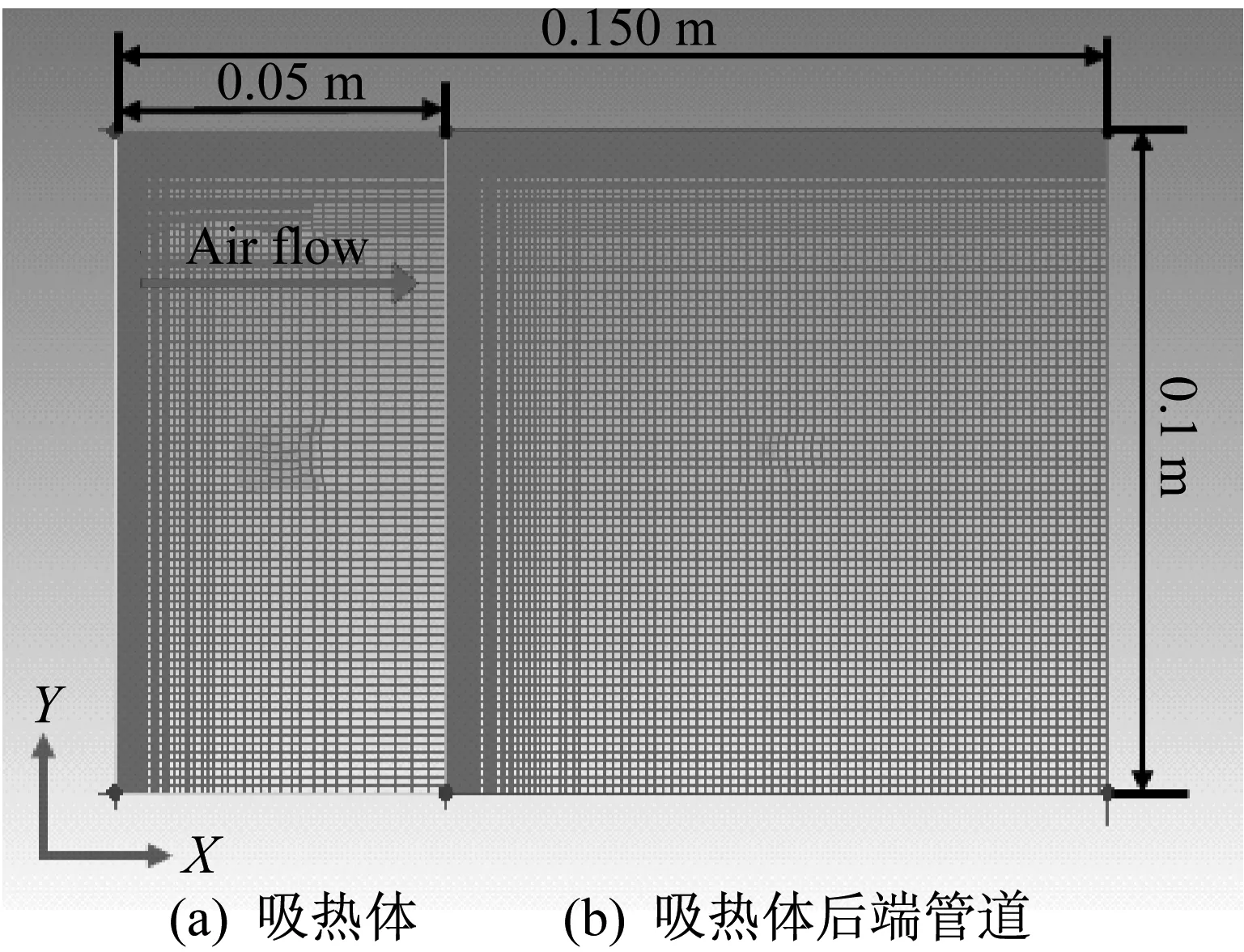
图2 吸热器模型网格划分示意图
2 仿真结果与分析
平均孔径与孔隙率是决定多孔介质的两个最重要结构参数,本文开展了该两个参数对吸热器特性的影响规律分析,对比了不同平均孔径和孔隙率的吸热体下吸热器内部温度和压强在稳态下的分布。
2.1 吸热体平均孔径对吸热器性能的影响
根据本文模型仿真得到的不同平均孔径的泡沫陶瓷吸热体下吸热器内部温度分布云如图3所示,各平均孔径对应的吸热器中轴线温度分布曲线对比如图4所示。从图3和图4可以看出:不同平均孔径下吸热器内部温度场及中轴线温度分布曲线相差较小,即泡沫陶瓷吸热体的平均孔径对吸热器内部温度分布影响不大。
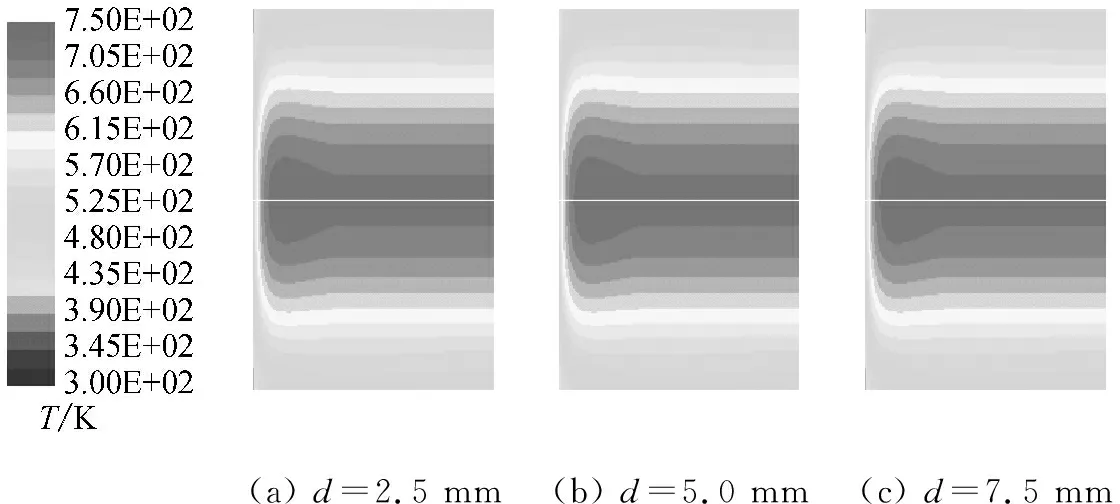
(a) d=2.5 mm(b) d=5.0 mm(c) d=7.5 mm
图3不同吸热体平均孔径下吸热器内部温度分布云图
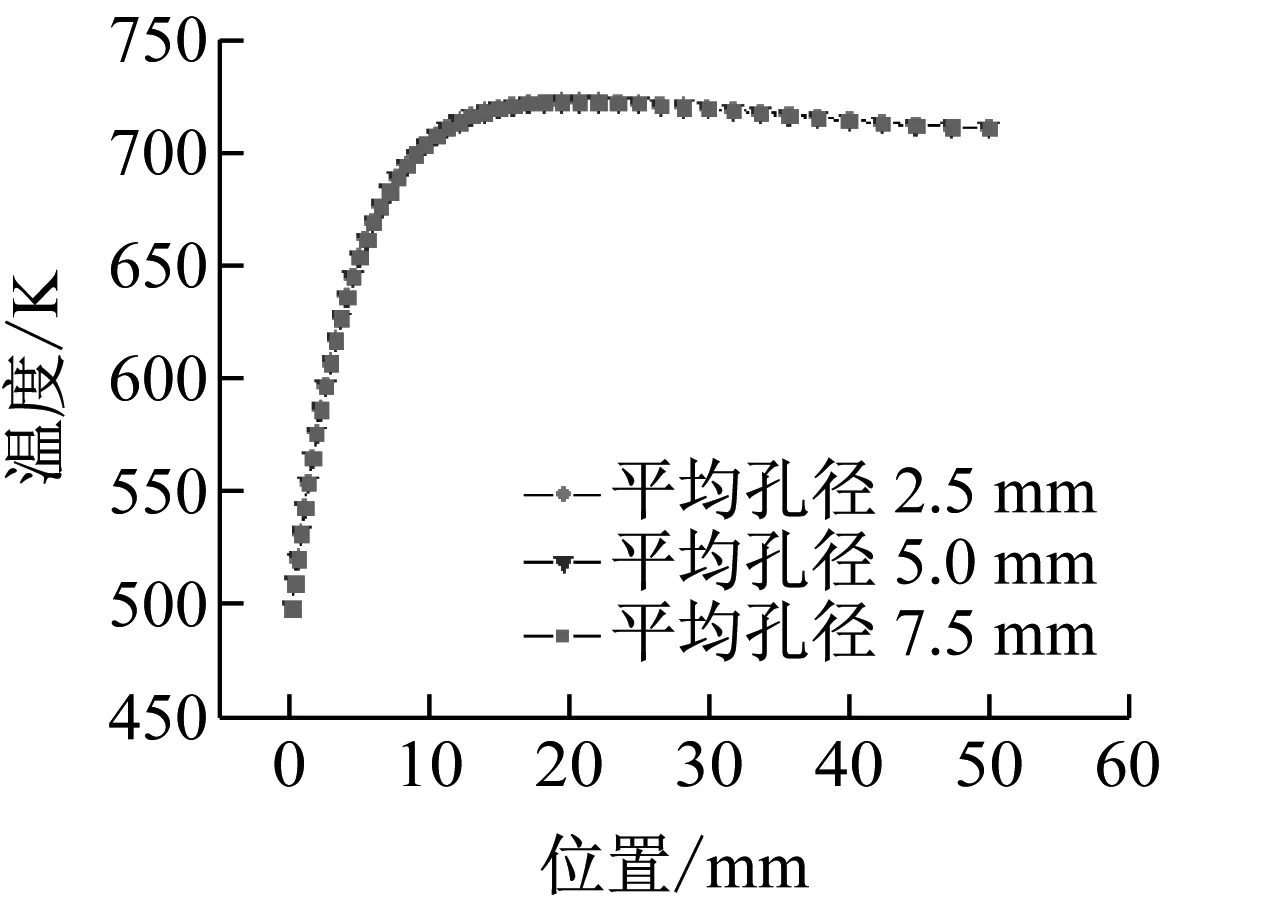
图4不同吸热体平均孔径下吸热器中轴线温度分布曲线图
根据本文模型仿真得到的不同平均孔径的泡沫陶瓷吸热体下吸热器内部表压分布云如图5所示,各平均孔径对应的吸热器中轴线表压分布曲线对比如图6所示。由图5和图6可以看出平均孔径越大,压降越小,即压力损失越少,吸热器内部流阻也就越小。其原因在于泡沫陶瓷吸热体的平均孔径越大其渗透系数越大、惯性系数越小,通过平均孔径对泡沫陶瓷渗透系数、惯性系数及吸热体内部温度场的综合影响,使得平均孔径越大,吸热器出口空气压强越高,即空气流经吸热器的压力损失越小。

(a) d=2.5 mm(b) d=5.0 mm(c) d=7.5 mm
图5不同吸热体平均孔径下吸热器内部表压分布云图
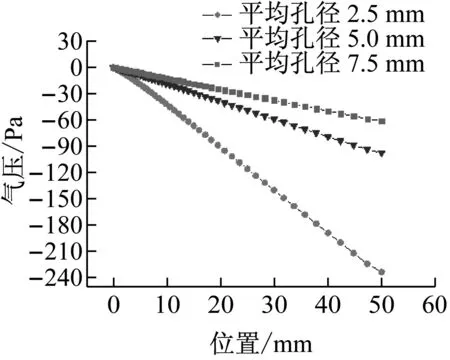
图6不同吸热体平均孔径下吸热器中轴线表压分布曲线图
2.2 吸热体孔隙率对吸热器性能的影响
根据本文模型仿真得到的不同孔隙率的吸热体所对应吸热器内部温度分布云如图7所示。各孔隙率对应的吸热器中轴线温度分布曲线对比如图8所示。
从图7和图8可以看出,吸热体孔隙率越大,吸热器内部温度也就越高,其原因在于孔隙率越大,消光系数越小,使得更多的太阳辐射穿透到吸热体内部,从而获取更高的吸热器内部和出口空气温度。

(a) 孔隙率0.6(b) 孔隙率0.7(c) 孔隙率0.8
图7不同吸热体孔隙率下吸热器内部温度分布云图
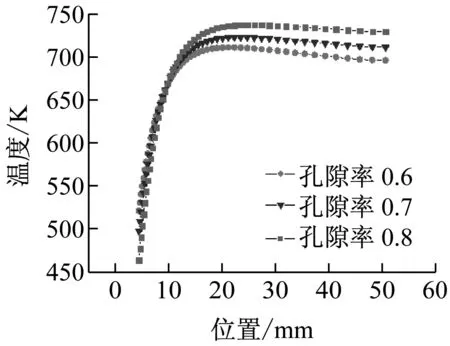
图8不同吸热体孔隙率下吸热器中轴线温度分布曲线图
根据本文模型仿真得到的不同孔隙率的吸热体所对应吸热器内部温度分布云如图9所示。各孔隙率对应的吸热器中轴线温度分布曲线对比如图10所示。
由图9和图10可以看出孔隙率越大,压强越小,即压力损失越少,吸热器内部空气流阻也就越小。在其他参数不变的情况下,泡沫陶瓷吸热体孔隙率越大则渗透系数越大、惯性系数越小,从而导致吸热体孔隙率越大,吸热器出口空气压强越高,即空气压损越小。

(a) 孔隙率0.6(b) 孔隙率0.7(c) 孔隙率0.8
图9不同吸热体孔隙率下吸热器内部表压分布云图
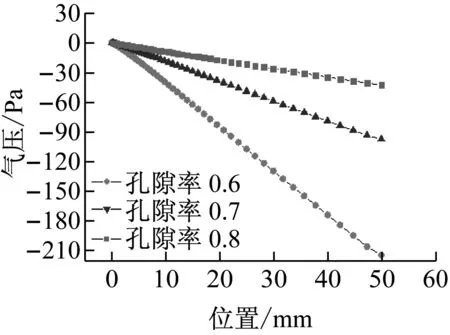
图10不同吸热体孔隙率下吸热器中轴线表压分布曲线图
3 结 语
本文通过建立泡沫陶瓷空气吸热器二维仿真模型,分析了吸热体平均孔径和孔隙率两个重要参数对吸热器性能的影响,得到如下结论:
(1) 在其他参数保持不变的情况下,吸热体平均孔径对吸热器温度场分布结果影响较小;泡沫陶瓷吸热体平均孔径通过对泡沫陶瓷渗透系数、惯性系数及吸热体内部温度场的综合影响,使得平均孔径越大,吸热器出口空气压强越高,即空气流经吸热器的压力损失越小。
(2) 在其他参数不变的情况下,吸热体孔隙率越大,吸热器内部温度越高;在孔隙率对泡沫陶瓷渗透系数和惯性系数的综合作用下,导致吸热体孔隙率越大,吸热器出口空气压强越高,即空气压损越小。
