视差贴图技术的研究与实现

2018-12-28任文婕

现代计算机 2018年34期

任文婕

（四川大学信息工程学院，成都610065）

0 引言

近年来，计算机图形学迅速发展，已经成为当今计算机专业领域内最为活跃的学科之一。它被广泛应用于当今生产生活的各个方面。如何更加逼真地表现三维图形的视觉效果是该领域中的一个很重要的课题。其中，纹理贴图技术，是近年来在计算机图形学领域中发展最快的致力于增强图形真实感的技术之一。它可以在不增加时间开销的前提下，更加方便地绘制真实感图形，而不用在建模阶段去考虑物体表面的细节。纹理贴图技术应用有助于增强场景绘制的真实感和降低模型的复杂度[1]。

传统的纹理贴图技术确有助益，但是当近距离观察采用纹理贴图技术进行绘制的物体时，其效果就大打折扣了。利用传统的纹理贴图技术可以呈现出物体表面的一些凹痕和细小的裂纹，但是这些细节仅仅通过颜色变化而被表现出来，它们更像是被直接涂染到物体表面上而并非客观存在的，整体的真实感太低。而现实中的物体表面大多并非光滑平坦，而是表现出无数凹凸不平的细节。

为了能真实地反映出这些细节，就必须研究更高级的纹理贴图技术[2]，那就需要对能进一步提高场景渲染效果的技术进行研究与实现。本文所论述的视差贴图技术就是一种更高级的纹理贴图技术，它在法线贴图的基础上增加了对高度的考虑，可以更真实地呈现出物体表面凸起的自我遮挡和运动视差的效果[3-4]。此外，本文论述的视差贴图技术还研究并实现了由于物体自遮挡而产生的自阴影的效果[5]。

1 算法实现

基本的法线贴图虽然能在一定程度上绘制出具有真实感的场景，但它也存在一些缺陷：它始终没有考虑表面细节的高度问题。当以一个较偏的角度去观察一个采用法线贴图技术绘制的场景时，这个问题就变得非常明显了：如图1 所示，表面的凸起看起来似乎太“矮”了，它没能挡住在藏它“身后”的凸起。这些凸起更像是被画在了表面上而不是实际存在的，场景的真实感太低。

图1 法线贴图效果

图2 视差贴图效果

视差贴图在法线贴图的基础上，充分考虑了物体表面的高度问题。它利用一张存储了片段高度值的高度图（Height Map）来模拟表面的高度场，通过修改片段对应的纹理坐标来使图像中的一个片段看起来比其实际的高度更高或者更低。如图3 所示，若利用高度图所记录的值来对物体表面进行位移，那么当沿着观察向量的方向去观察物体表面时，能观察到的应该是点B 处的场景。但实际的表面并没有被移动，观察射线最终会与物体表面交于A 点。这里，视差贴图巧妙地用点B 对应片段的纹理坐标去替代点A 对应片段的纹理坐标，然后再利用该纹理坐标去纹理图中采样颜色值并“贴”于A上，就可以获得一种仿佛看到了B 点的假象。

图3 高度对视觉效果的影响

因此，视差贴图技术所要解决的最重要的问题就是：如何根据点A 的位置、观察向量以及表面高度场找到点B 的位置，从而获得能体现深度感的，具有遮挡效果的场景。

1.1 高度场与观察射线的交点计算

实现高度场与观察射线的交点计算是整个视差贴图的关键所在。它直接决定了最终渲染效果的正确性和真实感程度。

首先，将高度图取反，获得一张存储了表面深度值的深度图，并将深度值规范化到[0,1]的范围内。如图4所示，多边形表面的深度值为0，最大的位移深度值为1。输入的纹理坐标为t0，偏移后的纹理坐标为toff，视差偏移向量为P（视差偏移向量的值决定了最大纹理坐标偏移量和偏移方向）。

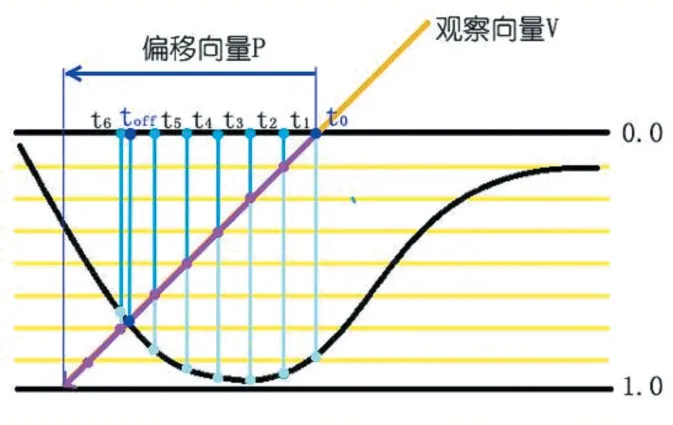
图4 逐层探索高度场与观察射线的交点

接着，将整个高度场分为n 层，层与层之间的距离相等，记为LayerDepth（LayerDepth=1/n）。再将视差偏移向量P 除以层数n，得到每次采样的步长△t（△t=P/n），这样做可以保证每次采样都是沿着视差偏移向量P 进行的。

然后，从输入的纹理坐标t0出发，逐层采样高度值：将当前层的深度值记为CurrentLayerDepth，当前纹理坐标值记为CurrentTexcoords。利用当前纹理坐标值，去深度图中采样，获得当前采样点的深度值CurrentSampleDepth。将CurrentLayerDepth 与CurrentSampleDepth 进行比较：

（1）若CurrentLayerDepth 小于CurrentSampleDepth，则将CurrentLayerDepth 加上LayerDepth（即移动到下一层），将CurrentTexcoords 加上采样步长△t（即移动到下一个采样点），然后重复上述操作；

（2）若CurrentLayerDepth 等于CurrentSampleDepth，则算法终止，此时，CurrentTexcoords 就是最终要输出的纹理坐标toff；

（3）若CurrentLayerDepth 大于CurrentSampleDepth（表明采样点高度已经低于表面），则停止继续采样。如图5 中的点t6所示，当前层的深度值大于从深度图中采样得到的深度值，而上一个采样点t5对应的层的深度值小于采样值。那么，此时观察射线与高度场的交点一定在t5和t6之间的某个位置。这里，可以利用相似三角形的特性，近似地估计出交点的位置：

图5 高度场与观察射线交点的估计

成功地计算出了最终要输出的偏移后的纹理坐标toff后，就可以利用它去法线图和颜色纹理图中采样获取表面细节信息了。最后再利用这些细节信息进行光照计算以获得最终的视差效果。

1.2 表面自阴影计算

通过上面交点的计算，物体表面的自我遮挡效果已经得到了很好的表现，但是因自我遮挡而产生的自阴影的效果却完全没有被表现出来，所以还必须要额外地进行表面自阴影的计算。

仍从交点O 出发，沿着光照射线进行逐层采样。在采样过程中，记录下所有CurrentLayerDepth 值大于CurrentSampleDepth 值的采样点，记为d1-dn。如图6所示，这些点阻挡了光照到达交点O。

图6 遮挡情况图

为了获得软阴影的效果，假设以一个面光源来照射物体，通过分析在面光源的照射下，遮挡物的大小以及遮挡物和被照射物体之间的距离与遮挡系数的关系，来粗略地表示出遮挡系数v。

图7 遮挡物较小的情况

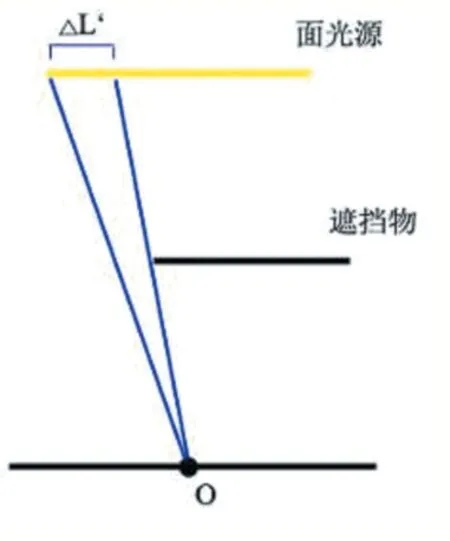
图8 遮挡物较大的情况

首先观察遮挡物的大小对阴影形成的影响。在图7 中，被遮挡物遮挡的物体表面上一点O 能接收到的来自面光源的光照强度为△L。在图8 中，其他条件均不变，仅遮挡物的大小变大（这里特指遮挡物向着遮挡面积变大的方向变大，表现在图8 中，就是遮挡物向左延伸。原因是：当遮挡物向右延伸时，虽然遮挡物的大小变大，但是它对光照不产生任何影响），此时点O 能接收到的光照强度变为△L’，△L’<△L。由此可得：在其他条件保持不变时，当遮挡物越大，物体表面接收到的光照强度就越小，最终的颜色也就越暗，相应地，遮挡系数v 就应该越大。即遮挡系数与遮挡物的大小成正相关。

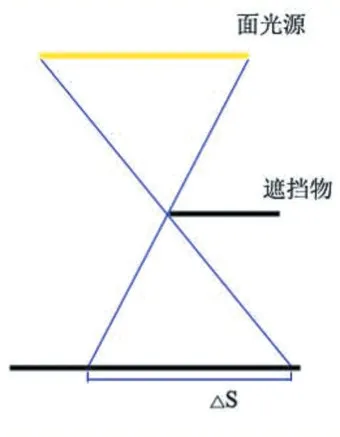
图9 遮挡物离物体较远的情况

图10 遮挡物离物体较近的情况

再来观察遮挡物的位置对阴影形成的影响。在图9 中，面光源在遮挡物的影响下，在物体表面形成的阴影大小为△S。而在图10 中，在其他条件不变的情况下，将遮挡物向更靠近物体表面的方向移动一定距离，形成的阴影大小变为了△S’。对比两幅图，可以明显看出△S>△S’。由此可得：在其他条件保持不变的情况下，当遮挡物与被照射物体之间的距离越小时，面光源在遮挡物的影响下在物体表面形成的阴影面积就越小（即半影的面积越小），半影的面积越小说明物体被遮挡得越严密，相应地，遮挡系数就应该越大。因此，遮挡系数和遮挡物与被照射物体之间的距离成反相关。

有了这两条结论后，就能轻松的得到一个粗略的遮挡系数值。然后将该值应用到光照计算中，通过色彩的明暗变化呈现出软阴影的效果。