基于归一化互相关的半透明遮挡视差估计
2022-01-28徐城
徐 城
(复旦大学计算机科学技术学院 上海 201203)
0 引 言
通过对人和部分动物的视觉原理进行研究,人们发现了双目视觉,它一直是计算机视觉中的一个重要的研究方向。通过对左右两个相机得到的不同位置的图像进行处理,恢复目标场景的部分三维信息。双目视觉系统设备简单、成本较低,因此可以被应用在很多领域,如汽车的无人驾驶[1-2]、视觉现象研究[3]、机器人导航[4]等。而对双目的研究也一直没有中断过,目前已经有了多种计算模型和方法,其中主要分为局部匹配法(如SAD、SSD等)和全局匹配法(如ELAS[5]、NLCA[6]等)。这些算法都有各自的优点和缺点:局部匹配算法速度快、实现简单,但比较依赖于图像中的纹理特征;而全局匹配算法则相对更为复杂、耗时更多,但在图像的低纹理区域的处理上更有优势。
然而在目前的双目视觉算法中,绝大多数算法在图片中同一个位置只会计算出一个视差,即满足唯一性约束条件。这在通常情况下都是合理的,且绝大部分数据集中也不会出现半透明物体,如KITTI数据集[7]和Middlebury数据集[8]。但事实上,在现实生活中,还是有很多的半透明物体,如带颜色的玻璃杯、彩色的透明塑料碗、透光的薄窗帘等。人或者相机在观察这些物体的时候,能同时观察到被这些物体遮挡的物体。这就导致了在图片中的同一个位置可能会对应多个现实物体。这种情况下,绝大部分的计算模型都不适用了,包括一些有很高精度、在数据集上有较好表现的模型[9-10],它们对视差的计算可能会被半透明的遮挡物干扰,最终得到的视差可能因为受到干扰而计算错误。这取决于半透明遮挡物和被遮挡物体的纹理信息、半透明物体的透明度等多方面因素。
目前也存在一些对半透明物体与材质的研究[11-12]。同时也有一些双目条件下对半透明遮挡的研究,如基于由粗到细的视差能量模型的算法[13],但该算法依赖于由粗到细的视差能量模型[14],有神经生物模型的普遍缺点,受感受野大小的影响且实验效果并不理想。同时,由于要计算各个朝向、大小的感受野响应,它的计算复杂度相对比较高。还有基于傅里叶变换、用于分离两幅叠加图片的算法[15],但该算法一般处理的是两幅图片叠加的问题,其中每幅图片各自的视差是相同的,因此也太不适用于处理现实中的半透明遮挡问题。
针对可能存在半透明遮挡的问题,本文进行了研究,首先比较了部分传统匹配代价函数。在存在半透明遮挡的情况下,一些仅依赖于灰度值变化的代价函数会受到较严重的影响,而本身就对噪声有鲁棒性的代价函数有较好的表现。然后,提出了一个基于归一化互相关(NCC)的代价函数来解决双层视差的问题。该方法是基于对应颜色区域的叠加实现的,在存在半透明遮挡和不存在半透明遮挡的情况下都适用,具有一定的鲁棒性。接着,本文同时求出了以左图像为基础的两层视差,和以右图像为基础的两层视差,并通过对比左右视差图去除了视差图中的部分误匹配点,提升了结果的准确性。最后,基于已有的双目图像数据集,本文模拟现实情况生成了部分带半透明遮挡的数据,并用这些数据来验证该方法的可行性。与一般双目匹配算法相比,本文算法对传统的匹配代价函数做了进一步的改进,从原来的单层视差拓展为双层视差,能处理存在半透明遮挡的情况,这就与普通的双目匹配算法有了很大的不同。而与其他一些处理半透明遮挡物的双目匹配算法比,本文算法在正确率和适用性上都有优势。此外,本文算法可以同时适用于存在半透明遮挡和不存在半透明遮挡的情况,这使算法在应用方面有了更大的灵活性,可以适用于不同的场景。
1 一般代价函数
1.1 存在半透明遮挡的双目系统
半透明遮挡在数据集中存在较少,而在真实世界中时有发生。当存在半透明遮挡时,通过相机得到的成像颜色是原物体颜色与半透明遮挡物颜色的结合。假设被遮挡物体透明度为0%,即不透明且只有一层的半透明遮挡。同时,在非半透明遮挡区域,假设存在透明度为100%的遮挡,那么在摄像机中成像的颜色计算如下:
C=C1×α+C2×(1-α)
(1)
式中:C是在照相机中成像显示的颜色;C1是被遮挡物体颜色;C2是半透明遮挡物的颜色;α是半透明遮挡物的透明度。通过这样的颜色叠加方法,就可以在现有的双目数据图像上叠加上半透明遮挡物,以生成实验数据。此外,半透明遮挡存在时的双目成像如图1所示,其中:OL、OR分别为左右相机的光轴中心;P1、P2表示被遮挡物体层上的点;T1、T2、T3表示半透明遮挡层上的点。xL,1和xL,2表示在左图像上的成像点;xR,1和xR,2表示在右图像上的成像点。

图1 存在半透明遮挡的双目系统
1.2 求取视差
通常,双目视差求取是基于代价函数的。图2显示了在随机点阵的实验中,部分代价函数在不存在半透明遮挡和存在半透明遮挡情况下的响应曲线。其中:(a)、(b)是对应的随机点阵图片,它是一个200×200的随机点阵,总体偏移为2像素,中心有一个80×80、偏移为6像素的矩形和一个120×120、偏移为10像素的半透明遮挡;(c)、(d)是SAD算法的响应曲线,响应值越小表示左图和右图的对应颜色块越相似;(e)、(f)是NCC算法的响应曲线,响应值越大表示左图和右图的对应颜色块越相似;(c)、(e)是不存在半透明遮挡的情况,(d)、(f)是存在半透明遮挡的情况。

图2 随机点阵图和SAD、NCC在不存在和存在半透明遮挡下的响应曲线
当半透明遮挡不存在的时候,左图像中的每个点都对应着右图像上的一个点。如图1中,对于点P1,左图中的xL,1对应着右图中的xR,1。当视差取到一个较合适值的时候,左图像上的点和右图像上的点重合,对应的代价函数通常有极大或极小值,如图2中(c)和(e)。但在半透明遮挡的干扰下,左图像中的每个点会对应右图像上的两个点。如图1,对于点P1,左图中的xL,2对应着右图中的xR,1和xR,2。在没有其他干扰的情况下,左图像上的点与右图像上两个对应点分别重合的时候应该有两个极大值或两个极小值,如图2中(d)和(f)。由此,可以得到一种最简单的双层视差的求解方法:取代价函数曲线中最大的峰值作为第一个视差,第二大峰值作为第二个视差。这样就可以得到两个视差的值,两者中较大的视差值代表半透明遮挡的视差,较小的视差值代表被遮挡物体的视差。
在使用取双峰值的算法时,使用不同的代价函数会有不同的结果。代价函数是用来表示左右两个图像相似性的函数。在视差计算中,通常使用的匹配代价函数有灰度值差绝对值和(SAD)、灰度值差平方和(SSD)、灰度值归一化互相关(NCC)等。在本文的研究背景中,图像中存在半透明区域,该区域在图像上显示的颜色是原物体和半透明遮挡物的结合。这就限制了很多代价函数的选择,如SAD和SSD在使用的过程中要求左右图像的对应点灰度相同。但在实际实验过程中,受到半透明遮挡物的影响,相同物体在左右两图上的对应灰度会有差别,这就导致了代价函数的可信度降低。NCC有一定的对噪声和光照变化的鲁棒性,这种特性可以在半透明遮挡的干扰下,有效地匹配物体。实验结果如图3所示。图3(a)是随机点阵图像,图3(b)和图3(c)分别是SAD算法得到的被遮挡物视差和半透明遮挡物视差,图3(d)和图3(e)分别是NCC算法得到的被遮挡物视差和半透明遮挡物视差,半透明遮挡物的透明度是50%。当透明度合适的时候NCC算法的结果要优于SAD算法,这显示了它对干扰的鲁棒性。因此,在之后的实验中,本文直接对NCC的代价函数进行优化,而不再考虑SAD和与SAD类似的SSD等代价函数。

图3 随机点阵图和SAD、NCC分别采用取双峰值算法的双层视差结果
取双峰值的方法能在一定程度上求出被遮挡物的视差和半透明遮挡物的视差。但这样的算法有一个很大的问题,在没有被半透明遮挡物遮挡的区域,算法仍然会去求第二个峰值,这会使结果出现很大的偏差。在非随机点阵图片中,这个问题更加明显。如图4所示,(a)和(b)是左右两图,其中图片左上部分有一块半透明遮挡;(c)和(d)分别是求出的被遮挡物视差和半透明遮挡物视差。可以发现,在被遮挡区域,该算法能在一定程度上求出被遮挡物的视差和半透明遮挡物的视差。而在被遮挡的区域外,该算法的结果并不理想。

图4 存在半透明遮挡的左右图像和取双峰值算法得到的双层视差
2 改进的代价函数
前文中基于NCC的双层视差计算有一个显著的问题,那就是对非半透明区域没有鲁棒性。即在非半透明遮挡区,该算法会强制计算出另一个视差结果,这个视差会影响正确的视差,这是在结果中不希望看到的。因此,需要对NCC的代价函数进行改进,使其能使用与双层视差的求解。对NCC算法的改进有很多种,但它们一部分是为了提高算法结果的精度[16],另外一部分都是为了加快匹配速度[17-19],这些改动与NCC本来的性质无关。本文在对NCC算法进行改动时选择在原算法上进行改动。在存在半透明遮挡的情况下,左图像上的一个点在右图像上有两个对应点,如图1所示,点xL,2中的信息部分包含在点xR,1中,部分包含在点xR,2中。因此希望点xL,2能同时与xR,1和xR,2比较。本文最终把右图像上两个对应点与它们的领域所对应的图像块叠加,得到一个包含了右图上两个对应点上所有信息的图像块:
(2)
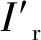
基于这样的想法,对NCC的代价函数进行改进。NCC算法的原代价函数如下:
(3)
(4)

(5)
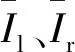
(6)
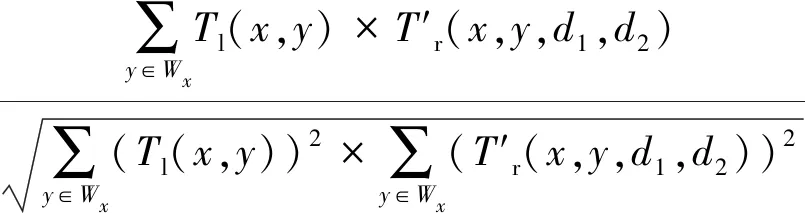
(7)
式中:d1、d2是对应的两个视差,且不妨让d1≤d2,这样d1就代表了被遮挡物体的视差,d2就代表了半透明遮挡物的视差。由此,就得到了一个与二重视差相关的函数。固定x,遍历d1和d2,求使Fl(x,d1,d2)最大的d1和d2,就是最后得到的视差值。
改进结果如图5所示,(a)和(b)两图像分别是被遮挡物体的视差和半透明遮挡物的视差,原图左右图像如图4中(a)和(b)所示。可以看到,在存在半透明遮挡物的区域,该算法结果与直接用NCC算法取双峰值的结果相差不大,但是在不存在半透明遮挡的区域,其结果要远优于直接用NCC算法取双峰值的结果。

图5 改进的NCC代价函数得到的基于左图的双层视差结果
图5的结果是以左图像为基础得到的视差图。同样,可以用右图像为基础得到对应的视差图。在半透明遮挡的区域,右图中的某一点同样在左图中有对应的两个点。因此,基于上文,可以得到类似的公式:

(8)
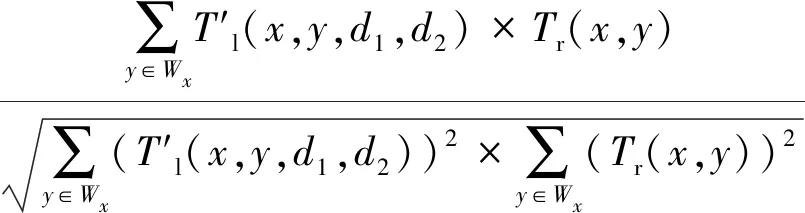
(9)
这样,可以得到以右图为基础的视差图如图6所示,(a)和(b)两图像分别是被遮挡物体的视差和半透明遮挡物的视差,原图左右图像如图4中(a)和(b)所示。

图6 改进的NCC代价函数得到的基于右图的双层视差结果
从实验结果可以看到,在半透明遮挡区域,算法会分别得到被遮挡物体的视差和半透明遮挡物的视差;而在没有被半透明物体遮挡的区域,算法会直接以原本场景中物体的视差为被遮挡物的视差和遮挡物的视差。这相当于紧贴着物体有一层透明度为100%的遮挡物。另外,可以发现在结果图像中仍有一些错误的点,如在部分遮挡区域,由于半透明遮挡物的特征太突出,算法没有求出被遮挡物的视差。为了对这些错误点进行校正,提升结果质量,需要对视差结果进行校正。
3 视差校正
3.1 去除不可信视差



图7 根据左右校正去除不可信视差后得到的双层视差结果
此外,根据领域一致性,还有一些点是不可信的,就是那些与邻域点的视差有很大差别的点,这些点虽然经过了左右校正,但仍然可能是计算错误的点。所以,当某个点的视差远大于或远小于它周围的大部分点的时候,认为这个点的值是不可信的。在实现过程中,取阈值q,当某个点的邻域内,与它视差相近的点的比率小于q的时候,就认为这个点是不可信的。实验中取q=30%。去除掉这部分点后,结果如图8所示。

图8 根据邻域一致性去除不可信视差后得到的双层视差结果
3.2 视差填充
去除了不可信的视差后,需要对去除的视差进行填充。视差填充的方法有很多,如在DoubleBP[20]中基于颜色把图像分块后再进行平面拟合的方法,另外还有基于最近可信点视差的填充、基于邻域视差均值的填充等。由于存在半透明遮挡的情况,颜色信息会受到干扰,因此基于颜色分割的填充并不适用。本文结合了邻域的颜色信息和代价函数响应信息填充,对于一个需要填充的视差,取它邻域内与它颜色接近的点中代价函数响应值最大的那个点的视差作为填充视差,填充结果如图9所示,其结果要远优于图5中得到的结果。

图9 填充后得到的双层视差结果
4 验证实验
除了随机点阵的实验外,还需要其他的实验来验证本文算法的可信性,而包含有半透明遮挡的实验数据较难直接获得。因此,本文基于Middlebury数据集[8]自主生成了一些实验数据,图4中(a)和(b)也是其中一组。生成数据的方式是在原本的图像上叠加上一个半透明的颜色块,并保证这个半透明颜色块的视差要大于它所覆盖的图像的视差,因为在现实生活中半透明遮挡物不会出现在被遮挡物的后面。然而,半透明遮挡物的选择对结果会有很大的影响。如果遮挡物透明度过大,那么算法就会检测不到遮挡物,最终导致只能得到被遮挡物的视差。如果遮挡物透明度过小,那么算法就会检测不到被遮挡物,最终导致只能得到遮挡物的视差。如果遮挡物纹理过于简单,那么可能会把半透明遮挡物造成的颜色变化当成是光线造成的颜色变化,从而忽略遮挡物。如果遮挡物纹理特征过于突出,又容易忽略掉背后的被遮挡物。因此,需要一个有合适透明度和合适纹理的遮挡物。在实验过程中,本文结合了渐变色的纹理和随机点阵的纹理,生成了如下的遮挡物:

(10)
式中:It(x,y)表示半透明物体在第x行y列的颜色信息;Y_MAX是y的最大值;Random(0,1)表示随机取0和1中的一个数;β表示随机点阵纹理的占比,一般让渐变色的纹理比重更大,即让β<0.5。最后根据透明度和式(1),把它叠加在原图像的某一个区域中,生成一个实验数据。
最后得到的实验数据如图10所示,其中共有4大组,每大组中以一对左右图像为基础,又生成4个小组,总共16个小组。在每大组中,第一个小组的数据是没有半透明遮挡的,第2-第4个小组的数据中的半透明遮挡物的透明度分别是70%、50%和30%。从结果中可以看到,当不存在半透明遮挡的时候得到的两组视差虽然略有不同,但都是代表原图的视差,这说明该算法在没有遮挡物的时候也适用。当半透明遮挡物透明度是70%的时候,在被遮挡区域,算法能基本区分遮挡物和被遮挡物,并分别求出两者的视差。当半透明遮挡物的透明度是50%的时候,有部分被遮挡物无法识别,只能检测到遮挡物。当遮挡物透明度是30%的时候,基本上无法检测到被遮挡物,而只能求出遮挡物的视差。随着透明度的降低,遮挡物对被遮挡物的覆盖越来越明显,这与现实生活中的情况相符,一个物体越是不透明,就越难以观察到它遮挡住的物体。本文的算法对半透明遮挡区域的存在与否有一定的鲁棒性,能同时适应存在半透明遮挡物和不存在半透明遮挡物的情况,并且在半透明遮挡物的透明度处在一个比较合适的范围的时候,本文算法能得到一个较好的结果。

图10 生成的实验数据和根据改进代价函数得到的双层视差结果
此外,本文实现了基于NCC取双峰值的算法和基于由粗到细视差能量模型的算法[13]来与本文算法作比较,并在生成图像上对各个算法进行了实验,得到了它们的平均错误率,结果如表1所示。前两列是在半透明遮挡物覆盖率是100%的情况下各个算法的平均错误率;后两列是在半透明遮挡物覆盖率是50%的情况下各个算法的平均错误率。其中又分为半透明遮挡物的视差的错误率和被遮挡物体,即背景的视差错误率。
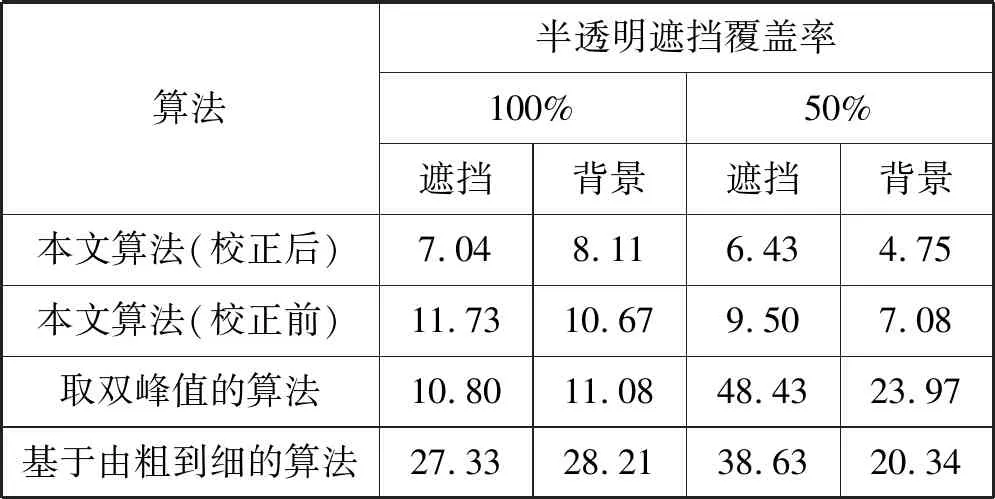
表1 各算法平均错误率(%)
实验中半透明遮挡物的透明度在30%~70%之间。由实验结果可以看到,当半透明遮挡物覆盖率是100%时,图像上每个点都对应着两个视差,这时基于NCC的取双峰值的算法有不错的结果,但当半透明遮挡物覆盖率下降到50%的时候,该算法的结果就产生了很多错误。这是因为该算法会在没有半透明遮挡的区域同样求出两个峰值,但该区域的物体只对应一个视差,额外求出的峰值会对结果判断产生干扰。而本文算法在半透明物体覆盖率是100%和50%的时候都有较好的结果。基于由粗到细视差能量模型的算法在两种覆盖率中的错误率都高于本文算法。此外,还可以看到,在经过视差校正后,本文方法的错误率有所下降,这表明在本文算法中视差的校正是有效的。
5 结 语
现实生活中存在很多半透明物体,但目前的双目视觉匹配算法基本不能适用于存在半透明遮挡物的情况,这会让部分双目视觉产品在实际应用的过程中发生错误。针对这个问题,本文研究了一般代价函数在存在半透明遮挡下的情况,在随机点阵中验证了基于代价函数取双峰值的方法,并找到了其缺陷。之后,本文改进了NCC算法的代价函数,设计了一种能同时适应存在遮挡物和不存在遮挡物情况的算法模型,并通过左右校正等方法对其结果进行优化。最后,本文通过实验验证了当遮挡物的透明度在合适的范围内时,该模型有较好的效果,可以被应用在双目视觉的各个领域以处理存在半透明遮挡的情况。
