C H F=C H C l分子的特性研究

梁冬梅 荆 涛 ＊ 孙光宇

（1.凯里学院理学院，贵州 凯里 556011；2.贵州师范学院物理与电子工程学院，贵州 贵阳 550018）

0 引言

近年来的实验和理论研究发现， 二卤代乙烯类化合物顺式构型的稳定性明显优于反式构型的稳定性[1-4]。并且，樊晓伟等[5]对化合物二氟代乙烯使用不同的基组进行计算发现， 使用小基组计算的总能量和轨道能量并不收敛， 甚至会给出错误的能级排序， 而使用较大基组计算的数值更接近于实验值。 因此， 为了给出正确的计算结果，本文使用与文献[5]相同的基组进行计算。

1 理论和计算方法

外电场存在时，哈密顿量H 可用下式求出，H=H0+Hint， （1）

上式中Hint的含义为， 当分子处在偶极近似条件下，外电场和分子体系之间的相互作用。 其表达式为，Hint=-μ·F （2）

在（2）式中，变量μ 表示偶极矩。

若哈密顿量Hint为零，有H=H0， （3）

从Grozema 等[6-7]创立的模型看，有外电场存在时的激发能Eexc为，

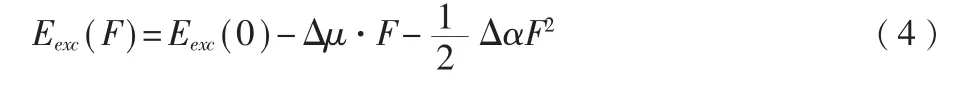
其中，在无外电场时的激发能，Eexc(F)=Eexc(0)。（5）

在上面的公式中包含了几个重要的量， 它们分别是加权因子、线强度和波数，用字母表示为gl、S、σ，加权因子的大小为1，线强度的单位为e2a2

0。

按照CHF=CHF 分子的标准坐标， 在B3LYP/6-311++G(3df, 3pd)基组的基础上对该分子的基态结构进行优化， 在此基础上对其激发态能量等物理量进行了计算。 所有计算均在Gaussian03 软件包[9]进行。

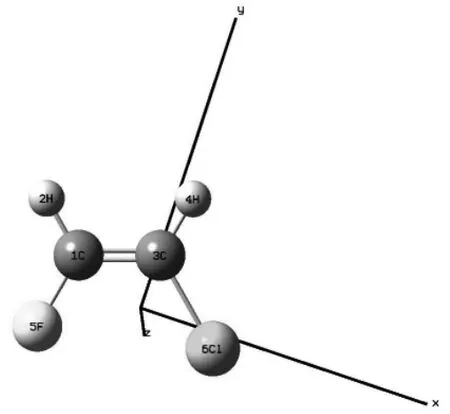
图1 CHF=CHCl 分子的基态结构

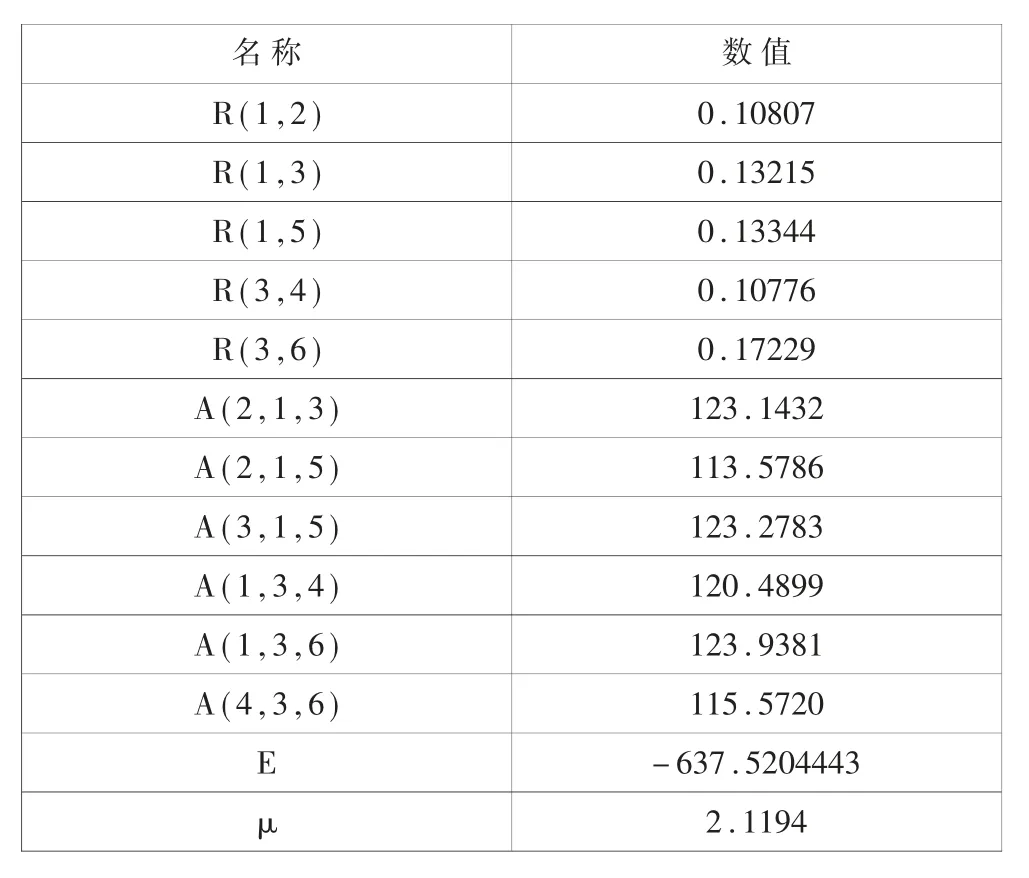
表1 优化的CHF=CHCl 分子基态键长(R/nm)、键角(A/deg)、总能量(E/a.u.)和偶极矩(μ/debye)

2 计算结果与讨论

2.1 CHF=CHCl 分子的基态稳定构型

CHF=CHCl 分子的结构如图1 所示。采用密度泛函理论(DFT)中的B3LYP，以6-311++G(3df,3pd)作为基函数，对其进行结构优化，得到该分子的基态键长、键角和总能，如表1 所示。

从表1 可以看出，分子的键长在0.10776～0.17229 nm之间变化，键角在113.5786～123.2783deg 之间变化，基态总能量为-637.5204443 a.u.，偶极矩为2.1194。

2.2 CHF=CHCl 分子的激发特性

在得到CHF=CHCl 分子稳定构型的基础上， 采用CIS-B3LYP/6-311++G(3df, 3pd)方法研究了该分子的前8 个激发态的激发能E、激发波长λ 和振子强度，如表2 所示。

表2 分子CHF=CHCl 的激发态能量、激发波长和振子强度

通过表2 可以得出以下规律， 分子从基态跃迁到前8 个激发态， 激发态能量不断增大， 激发态波长不断减少。 如图2 所示， 激发能从6.8258eV 增加到9.0568eV,而波长从181.64nm 下降到136.90nm。 振子强度就是振子数，从表2 可以看出，在从基态跃迁到激发态的过程中，振子强度并不为零，但大小不同。特别是从基态跃迁到第三个激发态， 振子强度f 达到了0.5218，有明显的电子跃迁发生， 而从基态跃迁到第七个激发态，振子强度f 为0.0325，振子强度比较小，在实验上即使有电子跃迁发生，也非常微弱，基本上观察不到。 其它从基态跃迁到此激发态(n=1,2,4,5,6,8)，振子强度非常小，在实验上观察不到跃迁发生。

3 结论

本文采用B3LYP/6-311++G(3df,3pd)方法得到了CHF=CHCl 分子的基态稳定构型， 讨论了分子的总能量、偶极矩和激发特性。 结论如下：

（1） 分 子 的 键 长 在0.10776 ～0.17229nm 之 间 变 化，键角在113.5786 ～123.2783deg 之间变化， 基态总能量为-637.5204443 a.u.，偶极矩为2.1194。

（2） 采用CIS-DFT 方法研究了分子的激发特性。分子的激发波长随激发能的增大逐渐减小， 变化的快慢与激发能的变化快慢相关， 但并没有在可见光区出现。 振子强度的大小不受激发能的影响， 电子跃迁的情况较为复杂。 从基态跃迁到第三激发态， 可以观察到明显的电子跃迁， 其它情况的振子强度较小， 基本上观察不到跃迁现象发生。