基于结构拓扑优化的绣花机压脚与针杆机构结构优化

2018-12-22季祖鹏顾萍萍

纺织学报 2018年12期

张雷，季祖鹏，顾萍萍

(浙江理工大学机械与自动控制学院，浙江杭州 310018)

电脑绣花机的针杆、压脚等机构在高速运动条件下会产生不平衡力和柔性冲击，对机头产生振动，进一步又对绣花机横梁产生较强的受迫振动，从而影响绣花机的可靠性、使用寿命及成品质量。许多学者对高速绣花机的研究围绕针杆以及挑线机构的运动学[1-3]、针杆机构扭转振动力矩[4]，以及针杆运动副间隙对位移精度和振动的影响展开[5]。对高速绣花机而言，有待于进一步围绕针杆及压脚机构协同运动展开分析。

针杆机构和压脚机构都是组合杆件，理论上可通过增加配重的方式来平衡机构高速运动下产生的惯性力。由于受空间和质量的限制，较多采用基于部分平衡理论对针杆机构及压脚机构进行平衡优化。研究表明，机头机构由于偏心质量引起的不平衡力及运动方向突变时产生的惯性力是机头振动的主要原因[6]。本文对某公司生产的绣花机装备进行分析，针对压脚、针杆机构的输出量进行比对，在结构拓扑优化的基础上用ICM(指独立连续映射，先定义独立连续的拓扑变量，通过映射及反演过程，使独立连续的拓扑变量逼近离散拓扑变量，完成拓扑变量“离散-连续-离散”的转化)方法[7-10]建立杆件的函数模型，对其主要结构进行优化，构成最佳传力途径，降低机构关键构件质量。

1 压脚与针杆机构的模型建立与分析

压脚与针杆机构作为高速电脑绣花机机头的主要执行部件，承担着刺绣的驱动工作。在主轴转速相同的条件下，由主轴向高速针杆凸轮、压脚高速轮凸轮分别传递转矩，在压脚连杆以及针杆连杆的驱动下带动压脚与针杆运动。

1.1 压脚机构柔性冲击分析

压脚机构的主要传动部件如图1所示，各部件构成压脚机构的传动路径。

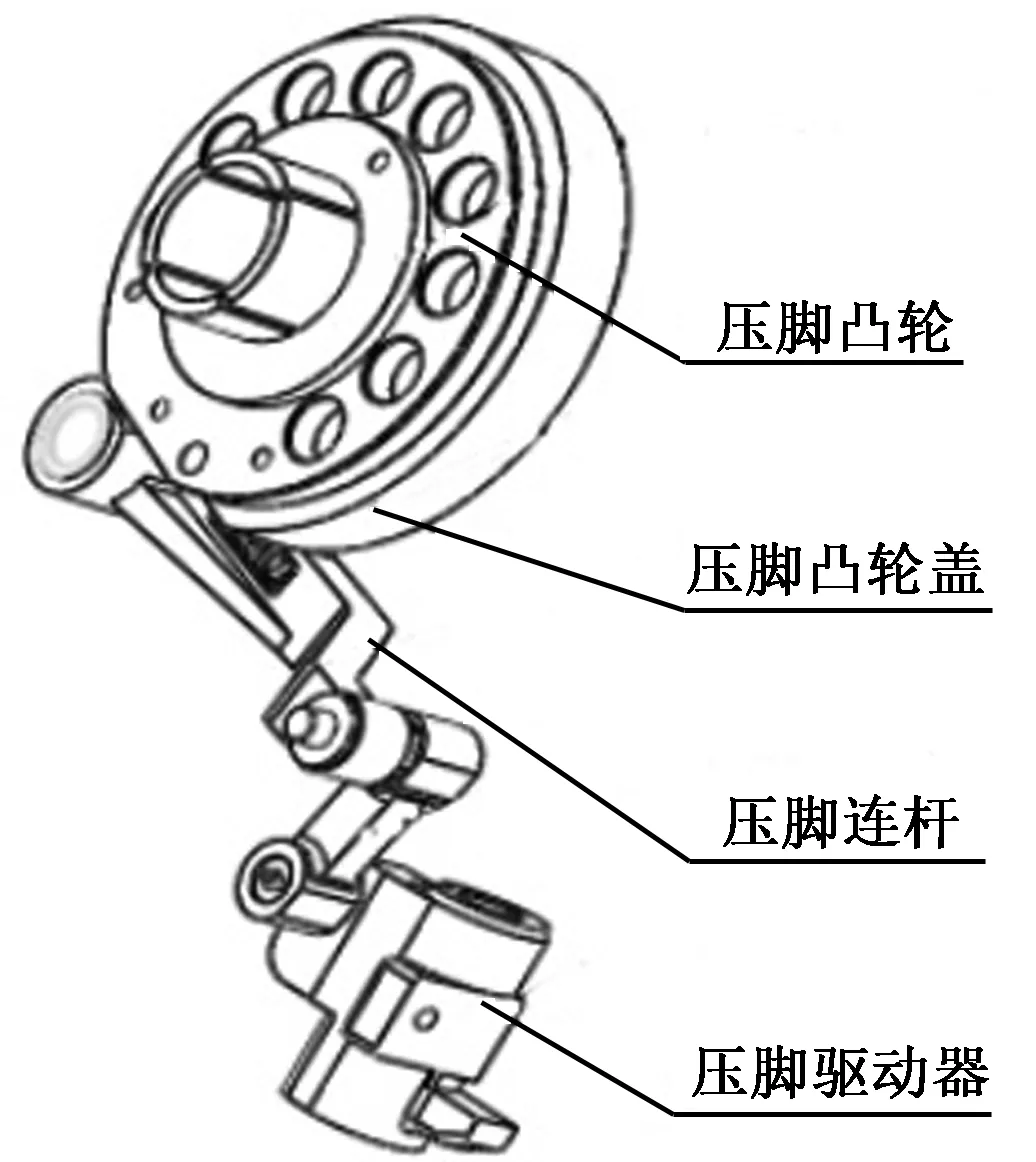
图1 压脚主要传动部件Fig.1 Main transmission parts of presser foot

图2示出压脚主部件质心速度变化(周期为0.1 s)。压脚滑块运动到极限位置时，在极限位置处产生一个停留，此时压脚凸轮的加速度产生一个突变，突变下压脚凸轮会对机头产生一个惯性冲击，惯性负荷远大于其工作负荷。高转速下此惯性负荷便引起扭转振动和横向振动，并存在相互耦合作用。

图2 压脚主部件质心速度随时间的变化Fig.2 Changes of centroid motion of presser foot with time

图3示出压脚主部件质心加速度变化。可以发现，压脚凸轮在周期运动瞬间产生的加速度突变要远远大于压脚滑块以及压脚连杆产生的突变值，这意味着同一周期里，压脚凸轮产生的柔性冲击影响最为明显。

图3 压脚主部件质心加速度随时间的变化Fig.3 Changes of centroid acceleration of presser foot with time

s从压脚凸轮的几何结构考虑，压脚凸轮为内槽凸轮的几何锁合型机构，由于滚子与凸轮槽之间存在间隙，在高速转动下会产生横越冲击，破坏电脑绣花机的工作稳态。从工程优化的实验角度考虑，减少冲击部件的质量有利于降低柔性冲击的冲量，一定程度上可提高绣花机工作的高速稳定性。

1.2 针杆机构柔性冲击分析

针杆机构的主要传动部件如图4所示，各部件构成针杆机构的主要传动路径。高速针杆凸轮是偏心凸轮，通过滚针轴承与针杆大连杆形成偏心连杆，整个针杆简化为一个四连杆与曲柄滑块的组合机构。

图4 针杆主要传动部件Fig.4 Main transmission parts of needle bar

图5、6分别示出针杆主部件质心速度和加速度随时间的变化。在针杆滑块运动过程中，针杆滑块运动呈现周期往复变化，滑块的加速度在针杆滑块带动机针抬升至极限位置时产生突变，类比压脚机构产生极大的惯性力，惯性力要远远大于工作载荷，对机针的运动工况造成不可忽视的影响。

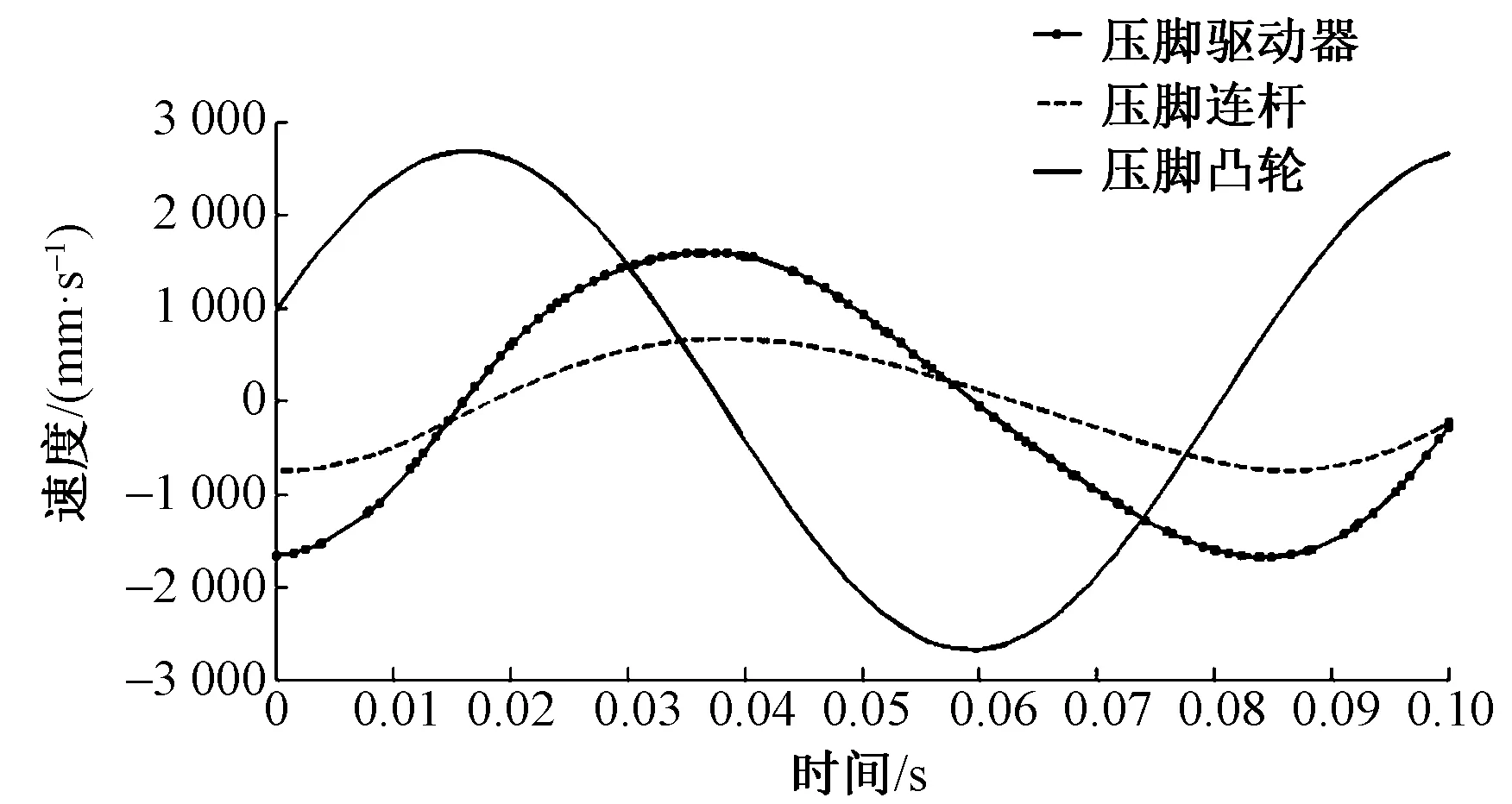
图5 针杆主部件质心速度随时间的变化Fig.5 Changes of centroid motion of main parts of needle bar with time

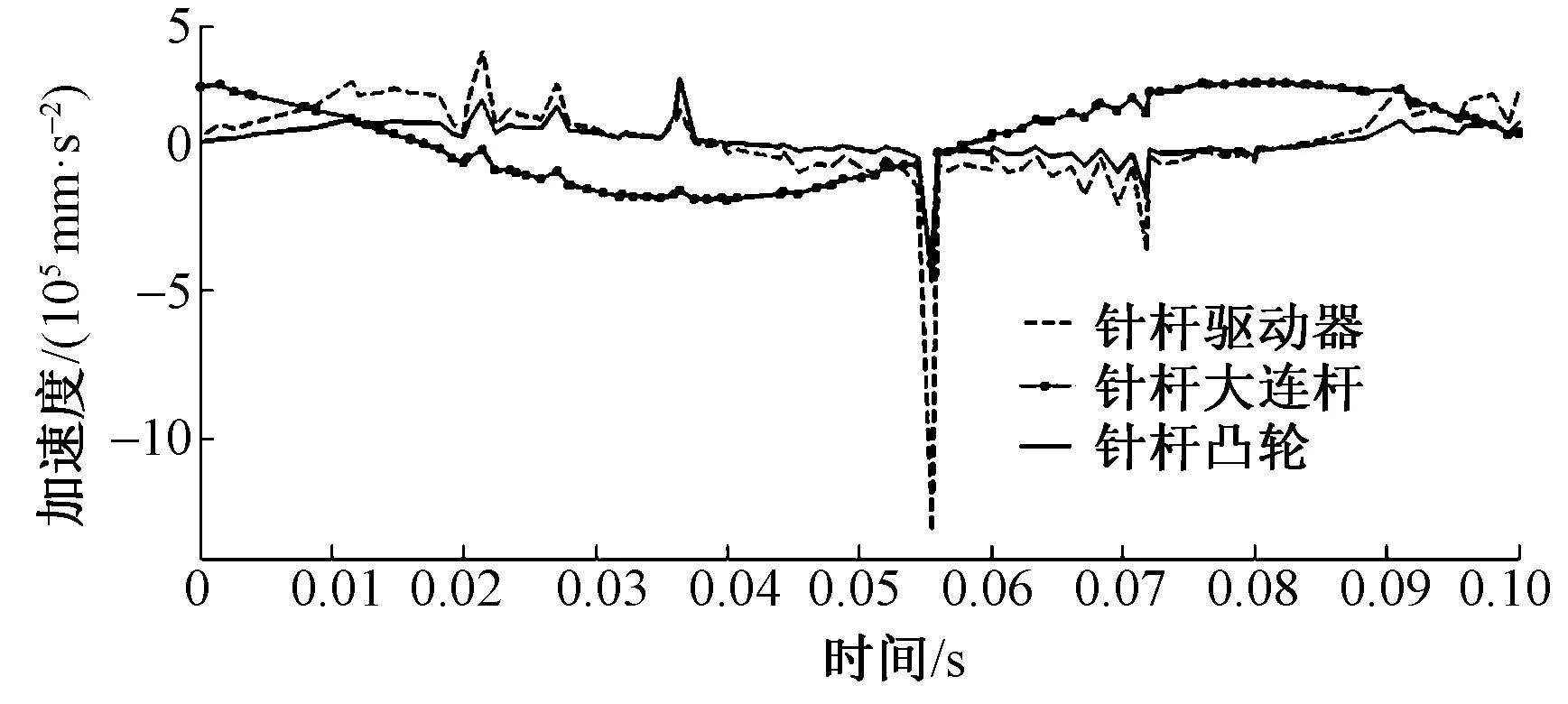
图6 针杆机构主部件质心加速度随时间的变化Fig.6 Changes of centroid acceleration of each rod of needle bar with time

2 压脚与针杆机构的ICM拓扑优化

ICM等一系列的拓扑优化方法都是在“基结构法”的基础上发展而来，所谓基结构法，就是将所设计的初始工作区域离散成适当的有限单元，通过算法来删除部分单元，形成带孔的连续体，完成拓扑优化的过程。机构拓扑优化涉及的算法是将物理量通过阶跃函数来表示拓扑变量，例如一个杆件的横截面积不管有多小，只要它不等于零，就定义其拓扑变量为1，一旦其几何数值变为零，则拓扑变量也就定义为0，如式(1)所示。

vi=1wi/w0i∈0,1

0wi/w0i→0

(1)

式中：vi为离散变量；wi为单元物理量(本文具体指代单元结构质量)；w0i为单元固有物理量。

ICM是在结构拓扑的基础上，以结构质量为目标，以应力、位移、频率等为约束目标连续体拓扑优化。该方法吸取了变厚度法和变密度法不需要构造微结构的优势，又使拓扑变量依赖尺寸和形状层面的弊端得到了有效地避免，使拓扑变量恢复了独立地位。根据柔性冲击原理，在无法改变加速度突变的工况下，只能针对机构的结构质量进行优化，结构单元刚度矩阵满足工况要求下，尽量减小单元质量，即将单元拓扑变量变为零，以最小的质量成本达到工况要求的强度和耐久性。

将设计区域先划分网格，部件上的网格都通过建立过滤函数的方式，再映射到阶跃函数上，用映射出的拓扑变量表示单个单元的实体状态。各网格可看做一个子域，子域的实际应力不可超过各子域的许用应力，按照ICM方法，零阶近似的应力约束下结构拓扑优化可表示为式(2)。利用式(3)～(5)对式(2)中的约束条件进行简化。

MinW=∑Ni=1fp(ti)wi0

s.t.t=(t1,t2,…,tN)T

pi≤fp(ti)p0i

0≤ti≤1 (i=1,…，N)

(2)

式中：t=(t1,t2,…,tN)T，为单元拓扑结构设计变量的向量；pi为子域(网格)在工况下的应力，Pa；p0i为子域(网格)的许用应力,Pa；N为单元拓扑变量的数目；fp(ti)为质量过滤函数；w0i为单元结构质量，g。其中求解W的最小值用Min表示，而该函数的约束条件用s.t.表示。

fp(ti)≥pip0i

(3)

pip0i=fp(t*i)

(4)

fp(ti)≥fp(ti*)

(5)

零部件受到的应力分解为垂直于截面的正应力σ→和切于截面的切应力τ→，其中只有τ→产生扭转变形，故可不考虑σ→。

由上述公式,可将式(2)变换为式(6)。

MinW=∑Ni=1fτ(ti)wi0

s.t.t=(t1,t2,…,tN)T

fτ(ti)≥fτ(t*i)

0≤ti≤1 (i=1,…，N)

(6)

式中:τi为子域(网格)在工况下的实际剪切应力,Pa；τoi为子域(网格)的许用剪切应力，Pa；fτ(ti)为重新定义的质量过滤函数。因每个子域切应力不随各单元截面大小改变而变化，而各子域(网格)的应力只同其内力和选用材料的性质有关，所以对于第i个单元截面，fτ(t*i)每次也是固定不变的。

引入过滤函数(7)，将fτ(t*i)进行迭代运算，初始ti*表示为τiτ0i。

fτ(ti*)=etiγ-1e1γ-1

(7)

式中，γ=0.062 1。计算得fτ(t*i)作为下一级的ti*，经过多次迭代求解，取fτ(t*i)<10e-12为停止迭代准则，再由所求的拓扑变量的函数值fτ(t*i)映射回离散变量0或1，由fτ(ti)表示，对比式(1)，定义为删除子域(网格)或保留子域(网格)，将满足切应力要求的子域(网格)区域进行省略。

3 压脚凸轮及针杆凸轮优化实例分析

以压脚凸轮与针杆凸轮为样本进行质量优化时，压脚凸轮以及针杆凸轮外形尺寸已被确定，假设压脚凸轮与针杆凸轮在高速运转情况下不发生塑性变形，通过ICM结构拓扑优化，量化单个结构的质量，在满足强度要求的条件下，达到更轻巧的结构质量要求。将模型压脚凸轮(材质为聚甲醛(POM)热塑性结晶聚合物，许用切应力τ0i=66 MPa)以及模型针杆凸轮(材质为高碳铬轴承钢GCr15，许用切应力τ0i=147.5 MPa)划分为若干子域，如图7所示。取单元网格面积最大划分网格，分别划分为356和167个网格。

图7 压脚凸轮与针杆凸轮网格划分Fig.7 Meshing for presser foot cam (a) and presser (b)

在有限元仿真分析中，主轴带动压脚凸轮及针杆凸轮转动，电动机转矩通过转轴传递转矩到针杆凸轮、压脚凸轮以及挑线凸轮上(因挑线运动范围及惯性力远小于另外二者，故忽略其影响)，将主轴贯穿压脚及针杆凸轮的文件导入有限元中，在主轴上添加转矩Me(Me=0.38 N·m)，在凸轮上添加边界约束进行仿真运算，继而查看切应力分布云图，得到压脚及针杆凸轮切应力参数的实际分布，将不同网格上分布的切应力τiτ0i作为初始ti代入式(7)进行迭代计算，经过映射得到的fτ(ti)，作为该网格删除与否的标准。

根据上述ICM几何方法对压脚凸轮及针杆凸轮进行优化，迭代结果如表1所示，优化结果如图8所示。与模型压脚及针杆凸轮相比，压脚凸轮结构质量减少了16%，针杆凸轮结构质量减少了38%，而与该公司实际采用的压脚凸轮及针杆凸轮相比，压脚凸轮结构质量减少了9%，针杆凸轮结构质量减少了13%。经对比，有效降低了对整个机构的振动冲击。