基于变量子域PCA的故障检测方法
2016-10-13王磊邓晓刚徐莹钟娜
王磊,邓晓刚,徐莹,钟娜
基于变量子域PCA的故障检测方法
王磊,邓晓刚,徐莹,钟娜
(中国石油大学(华东)信息与控制工程学院,山东青岛 266555)
针对工业过程监控中传统主元分析(PCA)方法没有突出局部变量信息的问题,提出一种基于变量子域PCA(variable sub-region PCA,VSR-PCA)的故障检测方法。首先使用PCA将原始数据空间分解成主元子空间(principal component subspace,PCS)和残差子空间(residual subspace,RS),计算变量与PCS的互信息来度量两者的相关性并以此划分变量子域。然后在变量子域中计算局部2统计量和局部SPE统计量,并通过贝叶斯推理整合所有子域的信息构造全局统计量,使得在利用所有过程信息的同时挖掘局部变量信息。在连续搅拌反应釜系统上的仿真结果表明,VSR-PCA方法具有更好的过程监控性能。
故障检测;主元分析;过程系统;动态仿真;变量子域;贝叶斯推理
引 言
现代工业系统规模日趋大型化和复杂化,有效的过程监控方法是保证工业过程安全、平稳运行的关键。多元统计过程监控(MSPM)方法——通过采集海量过程数据进行统计建模,无须精确数学模型,在过程监控领域得到了广泛应用[1-4]。主元分析(PCA)是一种应用广泛的多元统计方法[5-8],能够提取原始数据主要特征,建立统计模型。Wise等[9]最先将PCA方法用于过程监控,之后Ku等[10]考虑过程数据的时序相关性提出动态PCA模型,Wang等[11]针对非线性过程利用局部化方法提出非线性PCA模型。传统PCA是一种整体建模方法[12],其控制限描述的是过程的整体正常特征,没有体现局部变量信息。考虑到工业过程的故障主要体现在少数局部变量上,因此突出变量的局部特征具有重要意义。
针对传统PCA方法整体建模的缺陷,许多学者考虑“化整为零”的策略,利用分块技术突出过程的局部特性,提出多种监控方法,取得了很好的效果。针对过程变量较多,计算量大的问题, Cherry等[13]提出多块PCA方法,将变量划分为多个子块,分别建立PCA模型。Ge等[14]提出一种基于贝叶斯推理的多块PCA方法(BSPCA),使用多个线性子空间描述原始数据空间,在每个子空间建立主元分析监控模型。Ge等[15]提出分布式PCA方法(DPCA),通过不同方向的主元将原始特征空间分为多个子特征空间并分别建立PCA模型,在此基础上制定集成策略用于故障检测和诊断。Wang等[16]通过衡量变量的概率分布差异,将具有相似统计特征的变量划分在同一子块并在每个变量块里进行主元分析。上述分块PCA建模方法通过不同策略将被监控变量分为多个子变量组,能够有效挖掘局部变量信息,但是该类方法均要求子空间选取合适的变量个数,且同一变量可能被划分到不同子空间,造成信息冗余。此外该类方法需要建立多个PCA监控子模型,建模复杂程度显著增加。
针对传统PCA方法忽视局部变量信息挖掘的问题,本文提出了一种新的基于局部变量信息的PCA故障检测方法:变量子域PCA(VSR-PCA)。该方法通过变量与主元子空间的互信息大小划分变量子域,在子域建立局部统计量,并通过贝叶斯推理整合所有子域的局部信息构造全局统计量监控过程变化。本文方法的贡献在于:(1)提出使用互信息实现对变量子域的划分,有利于局部变量信息的挖掘;(2)不同于传统多块方法建立多个PCA统计模型,本文方法仅需建立一个PCA统计模型,通过对统计量的分块监控局部信息变化,模型复杂程度大大降低。本文最后利用CSTR的仿真结果验证方法的有效性。
1 主元分析
主元分析(PCA)是一种基于多元投影的线性降维方法。假设正常过程工况下有个传感器采集过程测量变量,每个传感器进行次采样,则构成数据矩阵。PCA模型将分解为
基于式(1),PCA建立两个监控统计量2和SPE来监视过程变化,如
2 VSR-PCA算法
VSR-PCA算法主要分为3个部分:通过计算变量与PCS的互信息大小划分变量子域;构造局部统计量描述局部信息;使用贝叶斯推理联合所有子域的信息构造全局统计量。变量子域的确立使得具有同种联系的变量划分到同一子域,且不同子域的变量具有一定的差异性;局部统计量可以更细致地反映过程的局部变化;贝叶斯推理构造全局统计量使得新的统计量依据权重的大小突出局部变量的信息。该算法的优势在于变量子域的构造无需任何先验知识,子域划分准则简洁明确,不会造成信息缺失或冗余;在一个PCA模型的基础上定义局部统计量描述局部变量的特征,无须多个PCA子模型,简化了建模过程。
2.1 变量子域的构造
传统PCA采用全局整体建模策略,掩盖了局部变量的信息,无形中扩大了正常状态的边界,造成较高的故障漏报。借鉴分块建模的思想,可以将全部变量依据某种联系划分变量子域,使得不同子域的变量具有差异性且子域内变量具有相似性。考虑到每个变量与PCS的相关性不同,与主元空间具有同等相关性强度的变量间必然有某种内在联系,因此根据变量与PCS相关性的大小划分为3个子域:子域1,强相关变量;子域2,相关变量(相关性强度具有过渡性);子域3,弱相关变量[17]。
在信息论领域,互信息是一种描述变量间相关性的测度,用来解释一个随机变量中包含的另一个随机变量的信息量[18-19]。互信息衡量的是共同拥有的信息,且具有非负性,因此本文使用互信息度量这种相关性。两变量和的互信息定义为
其中,窗宽参数由Silverman[20]提出的拇指法则获得
其中,为描述PCS的得分矩阵,为PCS的主元个数。衡量了变量与PCS共同拥有的信息,其值越大说明包含信息越多,亦即两者相关性越大。
则相应的变量与上述聚类结果一一对应,构造3个变量子域:变量子域1的组成为,表示此区间的变量与PCS相关性强;变量子域2的组成为,表示该部分变量与PCS的相关性强度具有过渡性,由强渐弱;变量子域3的组成为,表示变量与PCS相关性较弱。其中,表示该变量属于第个子域。3个子域的变量个数分别为、和,且满足。
2.2 局部统计量
变量子域构造完成后,计算局部2统计量和局部SPE统计量。相较于传统PCA方法中两个统计量度量整体过程变量的受控状况,该局部统计量描述的是局部变量的特征,因此可以更加细致地反映过程信息。以传统2统计量为例进行分析,其计算公式如
对应于3个变量子域,传统PCA方法中主元得分向量可以表示成
局部统计量的构造过程如图1所示。依据变量与PCS的互信息大小划分子域,划分准则简洁明确,同一变量不会出现在不同子域中;基于一个PCA模型构造局部统计量描述局部变量信息,简化了多PCA子模型的建模过程。另外,由于每个变量子域的维数不同且局部统计量是原2和SPE统计量的一部分,故相应的控制限由核密度估计得出,本文采用99%控制限。

图1 局部统计量的构造
2.3 子域监控结果的整合
本文采用贝叶斯推理策略[14]整合所有变量子域的信息。定义样本在子域发生故障的概率
通过全局统计量可以看出,发生故障时与故障具有较强相关的变量子域会获得较大权值,而较弱相关变量子域会获得较小权值,因此该全局统计量既能联合所有过程信息又能突出局部变量信息。
至此完成了VSR-PCA方法建模过程,该方法融合了分块思想和贝叶斯策略,体现了“先分后合”的建模过程。该方法依据变量与主元空间互信息的大小划分变量子域,使得同一子域变量具有较强相关性而不同子域具有差异性,不会造成信息冗余或缺失。同时,在一个PCA模型的基础上构造局部统计量描述局部变量特征,避免了因子块变量个数较少而难以建立PCA子模型的问题,简化了建模过程。此外,该方法采取贝叶斯策略集成所有局部统计量,能够有效突出局部变量信息。
3 基于VSR-PCA方法的故障检测方法
基于VSR-PCA方法的过程监控分为离线建模和在线监控两个阶段。图2是过程监控流程,具体步骤如下。

图2 基于VSR-PCA方法的过程监控流程
(1)离线建模
①采集正常过程数据并标准化预处理;
②使用PCA将数据分解为PCS和RS;
③依据变量与主元空间互信息的大小使用K均值聚类方法划分变量子域;
④在子域里计算局部2统计量和局部SPE统计量,控制限由KDE方法得出;
(2)在线监控
①采集新的在线数据标并进行准化预处理;
②将所有变量划分到不同的变量子域;
③在子域里计算新的局部统计量;
4 仿真实验
本文以一个典型的连续搅拌反应釜(CSTR)系统[21-22]作为仿真研究对象,以验证所提方法的有效性。CSTR系统结构如图3所示。

图3 CSTR系统结构
假设反应原料A经反应釜发生一级不可逆放热反应,生成产物B。此过程控制器完成两个主要的串级控制,一方面控制夹套冷却水流量保持温度稳定,另一方面控制出口流量保持液位稳定。
CSTR系统仿真过程测量10个变量,分别为4个状态变量和6个系统输入变量。仿真过程中采集1000个正常样本作为训练集;仿真表1所列的6个故障,各采集1000个样本作为测试集,其中前300个样本为正常数据,后700个样本为故障数据。6个故障中故障F1、F4和F5为阶跃型故障,故障F2、F3和F6为缓慢型故障。对于本文提出的方法,变量子域划分结果如表2所示,过程监控统计量以连续5个时刻超出控制限作为故障发生的标识。

表1 故障列表

表2 子域的变量组成
故障F1是进料流量发生阶跃变化,PCA和VSR-PCA的监控效果如图4和图5所示。从检测结果来看,2统计量和统计量均在第301个时刻检测出故障,且故障检出率几乎相同。PCA方法中SPE统计量在第306个时刻检测出故障,但其故障检出率只有27.86%,大部分时刻位于控制限之下,造成较高的漏报率;而统计量在第301个时刻,且检出率达到了100%,监控性能有了很大提高。图6为子域监控结果,可以看出变量子域2的两个局部统计量超出控制限非常明显而其他两个子域大部分在控制限以下。因此可以看出传统PCA方法容易掩盖局部变量信息,造成监控性能减弱,而本文方法恰好可以突出局部变量信息。
三皇治世时代太久远,研究考证难度很大,陕西安康或为女娲、伏羲真正的发祥地。今人当为弘扬华夏传统文化,紧密融合自然,发展生态旅游,加大汉江、伏羲山、女娲山、太极城的研究和开发力度,恢复建设高品位的、世人景仰的文化旅游圣地。

图4 故障F1的PCA监控结果

图5 故障F1的VSR-PCA监控结果

图6 故障F1的变量子域监控结果
当系统发生故障F6,即系统热交换效率下降,过程监控效果如图7和图8所示。从故障检测结果来看,PCA方法中统计量和SPE统计量分别在第433个和第356个时刻检测出故障,检出率分别为80.57%和91.86%;而VSR-PCA方法中两个统计量分别在第373个和第333个时刻检测出故障发生,检出率分别提高到了89.43%和95.29%,监控性能有了明显提高。从图9的子域监控结果来看,只有子域1的统计量超出控制限明显,进一步证明了本文方法可以突出局部变量信息,改善监控性能。
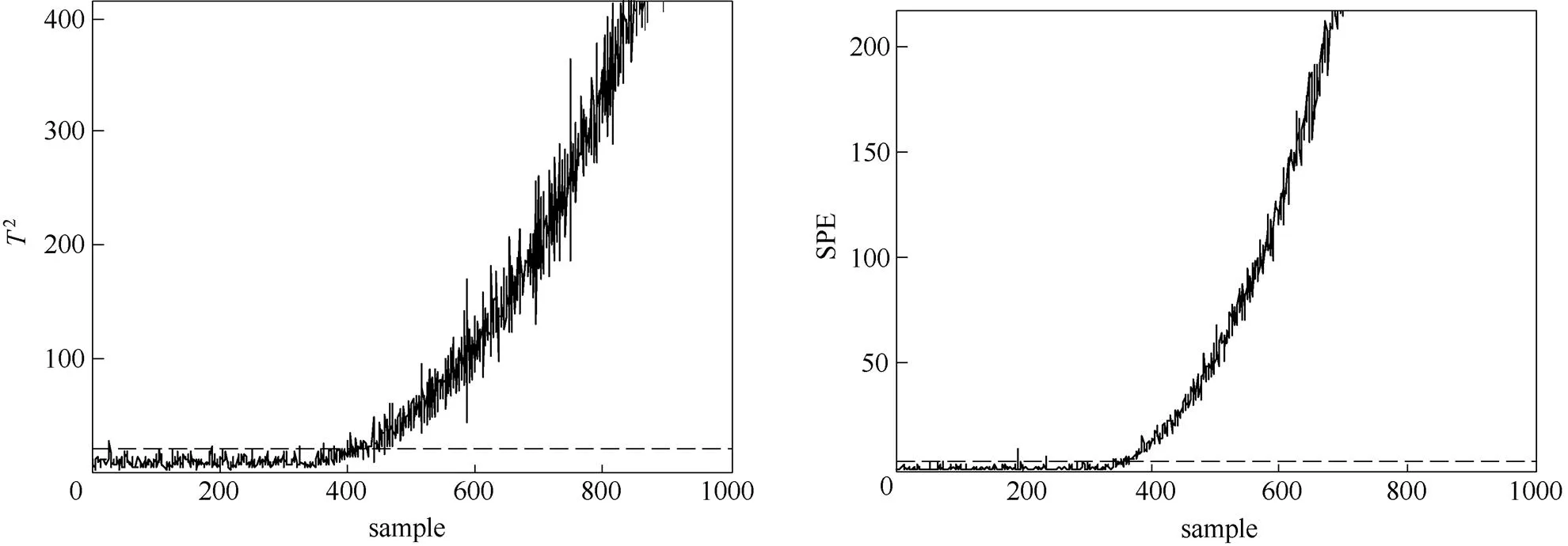
图7 故障F6的PCA监控结果
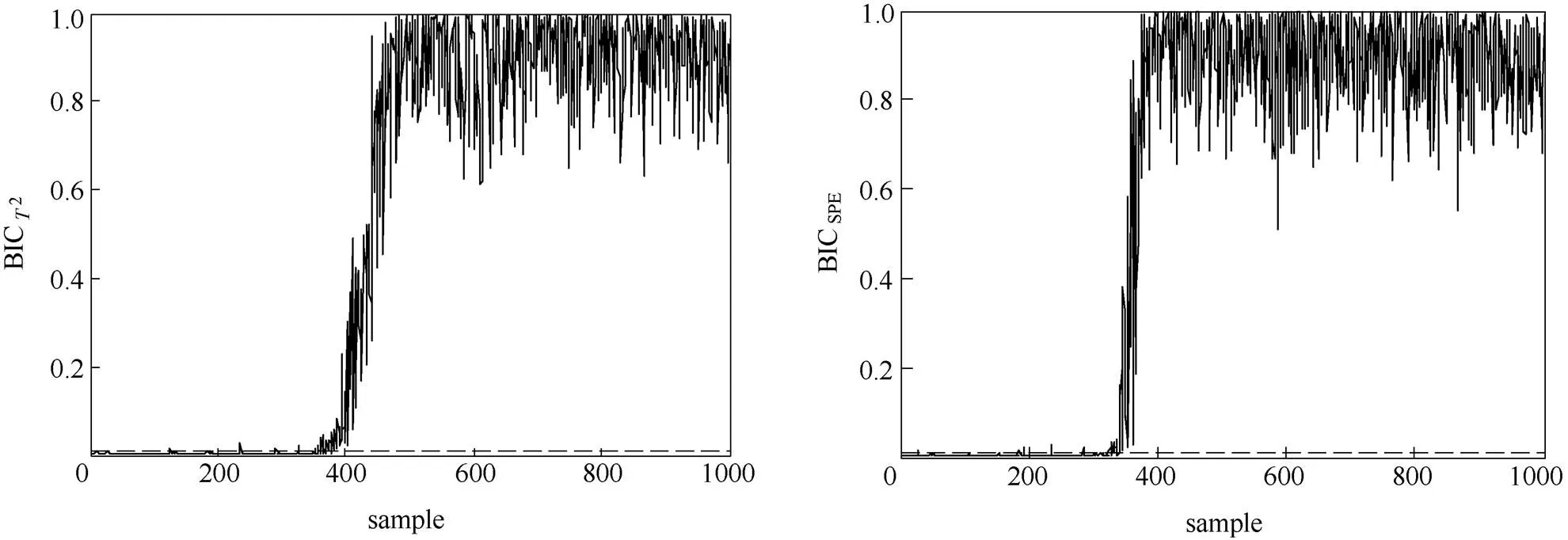
图8 故障F6的VSR-PCA监控结果

图9 故障F6的变量子域监控结果
为了进一步验证VSR-PCA方法的可行性,将其与传统PCA方法、文献[14]中的BSPCA方法进行比较分析,3种方法对CSTR系统6种故障的监控结果列于表3。可以看出,对于CSTR系统的6种故障,VSR-PCA、BSPCA方法相较于PCA方法均取得了更好的监控效果。以故障F4为例,传统PCA方法中SPE统计量故障检出率仅有13.43%,而其他两种方法的两个统计量故障检出率均达到99%以上,监控性能非常好。从6种故障的平均检出率来看,VSR-PCA和BSPCA方法均表现出很好的监控效果,并且VSR-PCA方法两个统计量的故障检出率要稍微优于BSPCA方法。

表3 故障检出率
总结对CSTR系统的仿真结果,传统PCA方法整体建模的思想使得局部变量信息被掩盖,无疑会减弱监控性能。BSPCA和VSR-PCA方法在利用全部变量信息的同时突出了局部变量的信息,可以更加细致地描述过程信息,提高了故障检出率。
其中,本文提出的VSR-PCA方法依据变量与主元空间的互信息大小划分变量子域,划分准则简洁明确,不会造成信息冗余或缺失,能够比BSPCA方法更好地挖掘局部信息,从而改进故障检测效果。
5 结 论
针对工业过程监控中传统PCA方法没有突出局部变量信息的问题,本文提出了一种基于变量子域PCA故障检测方法。该方法依据每个变量与PCS的互信息大小构造变量子域,进一步在子域里计算局部统计量,最后通过贝叶斯推理整合所有子域的信息建立全局统计量。CSTR系统的仿真结果说明,该方法能有效提高过程监控性能。
References
[1] GE Z Q, SONG Z H, GAO F R. Review of recent research on data-based process monitoring [J]. Industrial & Engineering Chemistry Research, 2013, 52 (10): 3543-3562.
[2] 解翔, 侍洪波. 多稳态化工过程的全局监控策略 [J]. 化工学报, 2012, 63 (7): 2156-2162.XIE X, SHI H B. Global monitoring strategy for multimode chemical processes [J]. CIESC Journal, 2012, 63 (7): 2156-2162.
[3] 钟娜, 邓晓刚, 徐莹. 基于LECA的多工况过程故障检测方法 [J]. 化工学报, 2015, 66 (12): 4929-4940. ZHONG N, DENG X G, XU Y. Fault detection method based on LECA for multimode process [J]. CIESC Journal, 2015, 66 (12): 4929-4940.
[4] KIM D, LEE I B. Process monitoring based on probabilistic PCA [J]. Chemometrics & Intelligent Laboratory Systems, 2003, 67 (2): 109-123.
[5] 许仙珍, 谢磊, 王树青. 基于PCA混合模型的多工况过程监控 [J]. 化工学报, 2011, 62 (3): 743-752.XU X Z, XIE L, WANG S Q. Multi-mode process monitoring method based on PCA mixture model [J]. CIESC Journal, 2011, 62 (3): 743-752.
[6] 夏陆岳, 潘海天, 周猛飞, 等. 基于改进多尺度主元分析的丙烯聚合过程监测与故障诊断 [J]. 化工学报, 2011, 62 (8): 2312-2317.XIA L Y, PAN H T, ZHOU M F,. Process monitoring and fault diagnosis of propylene polymerization based on improved multiscale principal component analysis [J]. CIESC Journal, 2011, 62 (8): 2312-2317.
[7] JIANG Q C, YAN X F. Just-in-time reorganized PCA integrated with SVDD for chemical process monitoring [J]. AIChE Journal, 2014, 60 (3): 949-965.
[8] DENG X G, TIAN X M, CHEN S. Modified kernel principal component analysis based on local structure analysis and its application to nonlinear process fault diagnosis [J]. Chemometrics & Intelligent Laboratory Systems, 2013, 127 (16): 195-209.
[9] WISE B M, RICKER N L, VELTKAMP D F,.A theoretical basis for the use of principal component models for monitoring multivariate processes [J]. Process Control & Quality, 1990, 1 (1): 41-51.
[10] KU W, STORER R H, GEORGAKIS C. Disturbance detection and isolation by dynamic principal component analysis [J]. Chemometrics & Intelligent Laboratory Systems, 1995, 30 (1): 179-196.
[11] WANG X, KRUGER U, IRWIN G W,. Nonlinear PCA with the local approach for diesel engine fault detection and diagnosis [J]. IEEE Transactions on Control Systems Technology, 2008, 16 (1): 122-129.
[12] YU J B. Local and global principal component analysis for process monitoring [J]. Journal of Process Control, 2012, 22 (7): 1358-1373.
[13] CHERRY G A, QIN S J. Multiblock principal component analysis based on a combined index for semiconductor fault detection and diagnosis [J]. IEEE Transactions on Semiconductor Manufacturing, 2006, 19 (2): 159-172.
[14] GE Z Q, ZHANG M G, SONG Z H. Nonlinear process monitoring based on linear subspace and Bayesian inference [J]. Journal of Process Control, 2010, 20 (5): 676-688.
[15] GE Z Q, SONG Z H. Distributed PCA model for plant-wide process monitoring [J]. Industrial & Engineering Chemistry Research, 2013, 52 (5): 1947-1957.
[16] WANG B, JIANG Q C, YAN X F. Fault detection and identification using a Kullback-Leibler divergence based multi-block principal component analysis and Bayesian inference [J]. Korean Journal of Chemical Engineering, 2014, 31 (6): 930-943.
[17] LI Y, XIE Z, ZHOU D H. Fault detection and isolation based on abnormal sub-regions using the improved PCA [J]. Journal of Chemical Engineering of Japan, 2004, 37 (4): 514-522.
[18] WANG J Y, WANG Y, ZHAO S G,. Maximum mutual information regularized classification [J]. Engineering Applications of Artificial Intelligence, 2015, 37 (37): 1-8.
[19] KRASKOV A, STÖGBAUER H, GRASSBERGER P. Estimating mutual information [J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2004, 69 (6): 279-307.
[20] SILVERMAN B W. Density estimation for statistics and data analysis [J]. Journal of the American Statistical Association, 1988, 83 (401): 600-620.
[21] DENG X G, TIAN X M. Sparse kernel locality preserving projection and its application in nonlinear process fault detection [J]. Chinese Journal of Chemical Engineering, 2013, 21 (2): 163-170.
[22] DENG X G, TIAN X M. Multimode process fault detection using local neighborhood similarity analysis [J]. Chinese Journal of Chemical Engineering, 2014, 22 (11): 1260-1267.
Fault detection method based on variable sub-region PCA
WANG Lei, DENG Xiaogang, XU Ying, ZHONG Na
(College of Information and Control Engineering, China University of Petroleum, Qingdao 266555, Shandong, China)
Aiming at the problem that traditional principal component analysis (PCA) method can’t highlight the local variable information in industrial process monitoring, this paper proposes a variable sub-region PCA (VSR-PCA) fault detection method. First, PCA is used to decompose original data space into principal component subspace (PCS) and residual subspace (RS), and mutual information between variables and PCS is calculated to measure their correlation which is utilized to obtain the variable sub-regions. Then, local2statistics and local SPE statistics are calculated in each variable sub-region. Bayesian inference is applied to integrate information in every sub-region to construct global statistics which are able to emphasize the local variable information while preserving the whole process information. Simulation results on the continuous stirred tank reactor (CSTR) system show that VSR-PCA method has better process monitoring performance.
fault detection; principal component analysis; process systems; dynamic simulation; variable sub-region; Bayesian inference
2016-02-29.
Prof. DENG Xiaogang,dengxiaogang@upc.edu.cn
10.11949/j.issn.0438-1157.20160217
TP 277
A
0438—1157(2016)10—4300—09
国家自然科学基金项目(61273160,61403418);山东省自然科学基金项目(ZR2014FL016)。
2016-02-29收到初稿,2016-05-13收到修改稿。
联系人:邓晓刚。第一作者:王磊(1992—),男,硕士研究生。
supported by the National Natural Science Foundation of China (61273160, 61403418) and the Natural Science Foundation of Shandong Province (ZR2014FL016).
