基于改进EMD算法的木材声发射信号特征研究

方赛银， 邱荣祖， 李 明

(1.福建农林大学 交通与土木工程学院，福州 350002；2.西南林业大学 机械与制造工程学院，云南 650224)

材料在受外力或内力作用产生变形或断裂时，以弹性波的形式释放应变能的现象称为声发射(Acoustic Emission, AE)。AE信号能够动态反映材料内部应力应变的产生和发展状况，从而为材料损伤提供了一种主动的无损监测方法。Ohuchi等[1]通过拉伸试验研究木材早晚材的AE特征，Ritschel等[2-3]利用AE事件数研究木材和层积材内部损伤的发展规律。孙建平等[4]研究木材在动态载荷下的AE事件的变化规律，郭晓磊等[5]利用AE特征研究木基复合材料内部损伤过程，丁小康等[6]根据AE信号特征研究木材干燥开裂过程。上述研究的主要依据是AE事件的相关统计参数，然而由于木材是多孔的各向异性材料，无论是AE信号的传播还是衰减规律都与金属等材料存在本质差异，仅靠AE信号的幅值来确定AE事件是不准确的。为此，徐锋等[7-9]提出根据AE信号的波形特征研究木材和胶合板损伤过程。

受信号采集噪声和衰减影响，信号降噪和波形析取成为木材AE信号分析的关键。木材AE信号是一种非线性、非平稳过程，目前主要采用小波技术进行AE信号时频域分析，然而小波核函数的选择及分解层数的确定都直接影响信号分析的结果。Huang于1998年提出了经验模态分解(Empirical Mode Decomposition, EMD)算法，为非线性和非平稳过程分析提供了完全自适应的分析方法，特别是分解后的固有模态函数(Intrinsic Mode Functions, IMF)具有明确的物理意义。包络拟合是EMD算法的核心，包络的不准确将导致信号分解的不完全。经典的EMD算法采用三次样条插值(Cubic Spline Interpolation, CSI)生产包络线，但三次样条插值算法容易产生过冲现象，进而影响EMD分解的准确性。为此，许多改进的包络拟合方法被用于EMD分解算法，其一是采用其它插值算法进行包络拟合，主要包括B样条插值[10]、分段幂函数插值[11]、分段Hermite插值[12]等。其二是通过增加插值点的方法提高包络精度[13]，但此类算法需要估算新的插值点，从而增加算法的复杂性。其三是通过不同的方法产生多条包络线[14]，然后在其中选择最优的包络拟合。

现有改进的包络拟合方法在一定程度上改善了包络的精度，但是往往付出了复杂性显著增加的代价，而且从本质上看，都是基于插值点上的函数值信息，没有引入新的关于节点信息。为此，本文根据EMD包络生成原理，增加插值点上的一阶导数信息，进而提出改进的分段三次Hermite插值(Improved Piecewise Cubic Hermite Interpolation, IPCHI)算法用于包络拟合。IPCHI算法能够在不增加算法复杂度的同时提高包络精度，同时有效避免三次样条插值过程中误差向数据内部传播而“污染”整个数据序列的问题。随后，基于IPCHI包络拟合方法提出改进的EMD算法。最后，针对木材受力弯曲过程的AE信号，提出基于小波降噪和EMD分解联合的AE信号分析方法，进而提出依据瞬时频率进行AE事件统计的方法。

1 经典EMD算法的基本原理

EMD算法的目的在于将信号分解为一系列表征信号特征时间尺度的IMF，再通过Hilbert变换获得信号的时频关系。理论上EMD算法可以处理任意非线性且非平稳信号，实际受IMF基本要求的限制，可进行EMD分解的信号通常需要满足以下三个假设：①信号至少有两个极值，即一个极大值和一个极小值；②信号特征时间尺度是由极值间的时间间隔确定的；③若数据没有极值点，可以将拐点的一阶或高阶导数值作为极值点。

此外，IMF还必须满足两个条件：①在整个数据长度上，极值点和过零点的数目必须相等或最多相差一个；②在任意数据点，局部最大值的包络和局部最小值的包络的平均必须为零。

EMD算法的基本步骤如下：

步骤1 确定给定信号x(t)所有的局部极大值点和极小值点。然后利用插值方法拟合出由所有极大值点构成的上包络线u0(t)和所有极小值点构成的下包络线v0(t)。

步骤2 根据下式计算上下包络线的均值：

(1)

将信号x(t)与m0(t)的差记为h0(t)=x(t)-m0(t)。

步骤3 判断h0(t)是否满足IMF的两个条件。若满足，则h0(t)为筛选出来的第一个IMF分量；如果不满足，则将h0(t)作为原始数据重复进行上述两个步骤，直到h0(t)满足IMF的两个条件。第一次筛选得到的IMF分量记为c1(t)。

步骤4 将c1(t)从原始信号x(t)中分离出来得到剩余信号r1(t)=x(t)-c1(t)。然后将r1(t)作为新的待分析信号，重复步骤1～步骤3，通过筛选得到第二个IMF分量c2(t)，再计算出余项r2(t)=r1(t)-c2(t)。重复上述步骤，直至得到的余项rn(t)是一个单调信号或rn(t)的值小于预先给定的阈值，分解结束。

经过上述4个步骤的计算，最终得到n个IMF分量，c1(t),…,cn(t)，余项为rn(t)，这样，原始信号x(t)可以表示为

(2)

由于筛选过程会平滑信号的幅值，从而“抹杀”信号的物理特性，所以实际应用时可以如下定义的阈值SD作为判断筛选结果是否为IMF分量的依据

(3)

其中T为信号序列的长度。SD也称为筛分阈值，一般在0.2～0.3之间取值。

2 改进的EMD算法

EMD算法主要通过插值拟合的方法生成信号的上下包络线。根据插值拟合理论，受龙格现象的影响，主要可以通过两个途径提高插值精度:①采用分段插值方法，即对插值区间进行细分，在每个小区间上采用低阶插值函数；②提供更多关于插值节点的有效信息。由于EMD算法的上下包络线是通过对极大和极小值点插值拟合生成的，所以插值区间取决于相邻两个极大或极小值点的距离，人为细分插值区间存在较大困难。因此，充分挖掘更多关于插值节点的信息成为改善拟合精度的有效途径。

根据EMD算法基本原理可知，包络线的所有插值节点都是信号函数的局部极大和极小值点，既然是函数的极值点，那么就可以合理地认为在插值节点上函数的一阶导数值为零，从而将关于插值节点的可用信息量提高一倍。由于三次样条插值是在整个信号区间上估算插值节点上的二阶导数值，所有在求解的过程中，各个点上计算值相互影响，必然会导致拟合误差的累积和传播。与三次样条插值不同，三阶Hermite插值仅涉及两个插值点，所以，在增加插值点一阶导数信息的基础上，采用分段三阶Hermite插值方法，不仅可以保证拟合的光滑性及精度，同时可以有效避免拟合误差的传播。

2.1 改进PCHI拟合算法

对于n个插值节点x=(x1,x2,…,xn)的CSI拟合问题，主要是利用n个插值节点上的函数值f(x)=(f(x1),f(x2),…,f(xn))估算所有内点上的二阶导数信息，具体通过求解一个关于插值节点二阶导数值的三对角线性方程组来实现，而且为了保证线性方程组求解的唯一性，还需要补充两个边界条件，显然在求解过程中，边界点上的误差将不断向信号内部传播，进而影响拟合精度。

PCHI拟合算法的基本原理是在每个小区间[xj-1,xj]，j=2,…,n上，依据两个插值节点xj-1,xj上的函数值f(xj-1),f(xj)和一阶导数值f′(xj-1),f′(xj)，采用三次多项式函数进行插值拟合，每个区间上的四个插值基函数如下所示

(4)

式中:x∈[xj-1,xj],hj=xj-xj-1,j=2,…,n。

因此，每个区间上的PCHI函数的表示

(5)

因为EMD算法中的信号包络线的插值节点都是局部极大和极小值点，根据极值点的定义，可以认为插值节点上信号的一阶导数值等于零，这样就增加了以下n个插值条件

f′(xi)=0,i=1,…,n

(6)

将上述插值条件代入式(5)，可以得到IPCHI拟合函数为

Hj(x)=f(xj-1)l0(x)+f(xj)l1(x)

(7)

根据上述推导，在每个小区间上，IPCHI算法仅需要构造两个插值基函数，从而有效降低了算法的复杂程度。此外，由于所有内点上的一阶导数值都相等，所以IPCHI至少能够保证与CSI拟合同样的光滑性，而且每个区间上的插值函数仅与该区间的两个端点信息有关，各区间上的插值函数保持相对独立，从而避免了CSI中拟合误差向信号内部传播的问题。

另外，根据插值理论，PCHI在整个信号区间上的拟合误差是

(8)

同样情况下的CSI误差是

(9)

通过上述两式的比较发现，CSI的拟合误差上限是PCHI的5倍，这也进一步说明了PCHI能够有效提高拟合精度。

2.2 数值试验

为了说明IPCHI的拟合效果，首先产生长度为100的随机信号，然后分别采用CSI和IPCHI生成信号的上下包络线,如图1所示。为了确保上下包络线能够覆盖全部信号，本文将信号两侧的端点视为极值点，具体处理过程是：若端点处信号为正值，则视为极大值点，同时对该点再赋以零值作为极小值点；反之，若端点处信号为负值，则视为极小值点，同时对该点再赋以零值作为极大值点。

图1 CSI和IPCHI包络拟合曲线

从图1可知,CSI拟合出现了明显的过冲现象，譬如在图1中的A和B处，CSI拟合后出现了新的极大和极小值点，类似的情况还在其它地方多次出现。

为了进一步说明包络的不准确对EMD算法的影响，本文分别采用CSI和IPCHI方法产生信号上下包络线，并进行一次信号分解，IMF分量的判断标准设定为SD=0.2，EMD分解后得到的第一个IMF分量,如图2所示。

从图2可知，两种插值算法下得到的分量都能满足IMF的两个基本条件，而且从幅值上可以明显看出EMD算法对信号的平滑作用。然而，通过比较发现，基于CSI拟合得到的IMF分量已经不能反映原始信号特征，特别是信号的后半部分已完全丧失了原始信号特征，显然这种不完全分解必然会影响其后的信号分析。与之相反，基于IPCHI方法得到的IMF分量能够很好地保留原始信号特征。

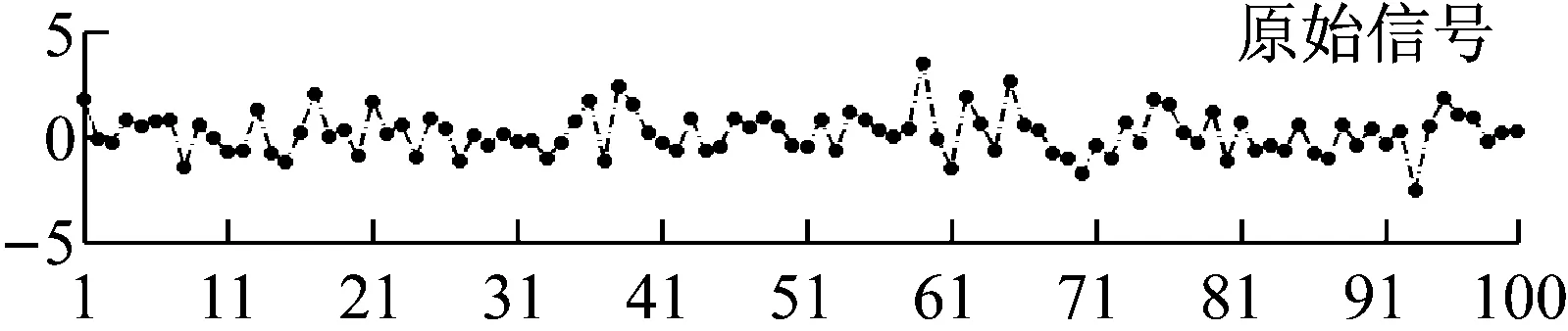
图2 基于CSI和IPCHI的EMD分解

3 基于改进EMD算法的木材AE信号分析

常规的参数分析法主要依据AE事件的属性，而由于缺乏有效的AE信号时频特性，通常只能根据AE信号幅值判断是否发生AE事件。然而，木材作为一种多孔的各向异性材料，受力过程释放的AE信号不仅类型丰富，而且存在更为明显的衰减特性，甚至会“淹没”在测量噪声中，实际使用时AE事件的确定和统计非常困难。为此，本文将采用EMD算法研究木材AE信号特征，首先利用小波技术对采集的原始AE信号进行滤波和波形重构，然后采用本文提出的改进EMD算法对对重构后的AE信号进行IMF分解，在信号相关性分析的基础上，确定能够反映木材AE信号特征的IMF主分量。最后通过对IMF主分量进行Hilbert变换，获得木材AE信号的特征频率，并进一步根据瞬时频率确定AE事件，从而赋予AE事件更为明确的物理意义。

3.1 木材AE信号采集平台

为了获得可靠的原始AE信号，本文采用专门的AE传感器和高速采集设备自行搭建木材AE信号采集系统，同时设计相应的软件平台。

AE信号采集系统主要由AE传感器、前置放大器、高速数据采集设备等组成,如图3所示。其中传感器选用声华SR150N单端谐振AE传感器，采集频率范围为22～220 kHz，且配备了40 dB的PAI前置放大器。数据采集设备选用NI的8通道的高速数据采集设备USB-6366，该设备最大采样频率可达2 MHz。现有研究表明木材AE信号特征频率通常在150 kHz以内，所以根据香农采样定理并保留一定的裕度，本论文在试验中设定的采样频率为500 kHz，采集的多通道AE原始信号在软件平台中分离后以数据文件形式保存。

3.2 试验设计

图3 木材AE信号采集系统

本论文主要通过三点弯曲力学试验获取木材AE信号。首先制作尺寸为400 mm×40 mm×13 mm的云南松(Pinus yunnanensis)试件，并确保试件尺寸均匀且无干燥缺陷。然后依据GB/T17657标准在力学试验机上进行三点弯曲力学试验,如图4所示。设定试件跨度为300 mm，载荷从5 N开始，以2 mm/min的进给速率进行加载，直至试件断裂为止。在试件表面施力点的两侧分别布置一个AE传感器。

图4 木材三点弯曲试验

3.3 木材AE信号分析

由于试验过程设定的采样频率较高(500 kHz)，所以完整的试验数据非常庞大，而本文主要研究EMD算法在木材AE信号分析中的应用，所以这里仅截取了试验后期一个长度为2 ms的数据片段,如图5所示。该片段共包含10 000个数据，所有的AE信号分析均在MATLAB中完成。

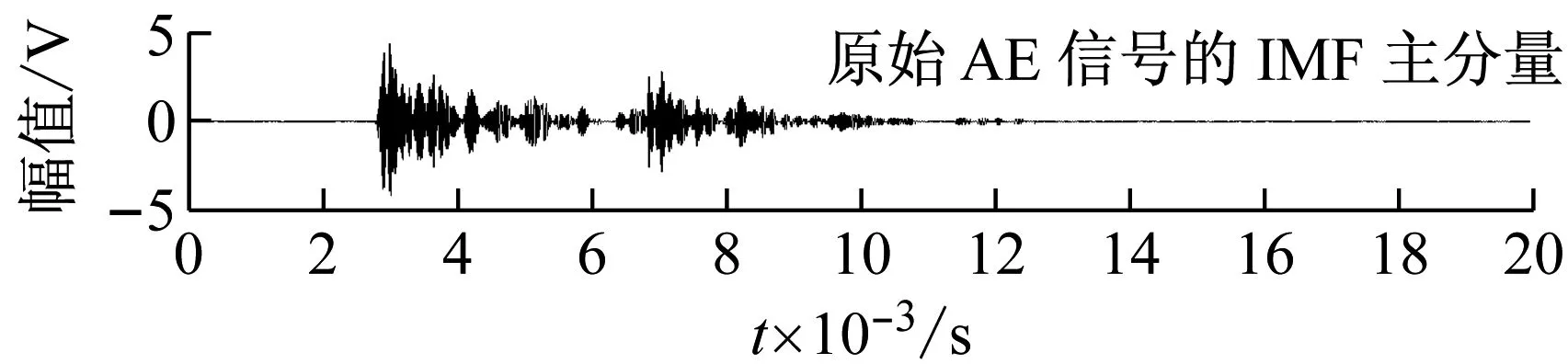
图5 AE原始信号和IMF波形

文献[15]研究表明，对AE信号进行小波预处理后，再进行EMD分解能够取得更好的效果。为此本文首先对原始木材AE信号进行小波降噪和波形重构，在小波分析时选择正交db小波作为核函数，并设定小波分解层数为8，由于小波分析不是本论文的重点，所以这里不再给出小波分析的详细过程。

为了说明小波预处理的作用，本文分别对小波处理前后两组AE信号进行EMD分解处理，经过本文提出的改进EMD算法自适应分解，分别获得13个IMF分量，为简单起见，这里仅列出了小波处理后AE信号EMD分解后的所有IMF分量及余项,如图6所示。

因为EMD分解具有非常明确的物理意义，IMF分量反映了信号在每个时刻的固有特性，因此，本文根据IMF分量与原信号的相关性来确定主分量，表1和表2分别为小波处理前后两组AE信号经EMD分解后，前4个IMF分量与对应原信号的相关系数。

表1小波处理前IMF分量与原始信号的相关系数

Tab.1CorrelationcoefficientsbetweenIMFsandoriginalAEsignals

IMFIMF1IMF2IMF3IMF4相关系数0.553 80.590 20.472 60.106 9

表2小波处理后IMF分量与原始信号的相关系数

Tab.2CorrelationcoefficientsbetweenIMFsandAEsignalstreatedbywavelet

IMFIMF1IMF2IMF3IMF4相关系数0.507 20.806 60.197 10.067 5

依据相关性比较，两组AE信号都可以将第2个IMF分量作为主分量,如图5所示。表1中数据显示所有IMF分量与原信号的相关性都不超过0.6，甚至前两个IMF分量相差无几，这主要是因为受噪声影响，EMD算法只能对AE信号进行很不完全的分解，介于这种原因，以相关性作为选择IMF主分量的依据也不再充分。与之相反，表2中数据说明经过小波预处理后，再进行EMD分解的效果明显提高，而且可以根据相关性条件容易选定第2个分量作为IMF主分量。

为了进一步研究AE信号的频率特性，本文分别对原始AE信号及其EMD分解后的IMF主分量、小波处理后AE信号的IMF主分量进行了频域分析，相应的频谱图,如图7所示。

图7显示未经小波预处理的信号频率分散，很难确定木材AE信号的特征频率范围，然而，AE信号经小波预处理后，IMF主分量的频域特性明显集中。根据IMF主分量的频率分布可以确定木材AE信号的特征频率中心位于46.5 kHz，为了通过瞬时频率判断AE事件的发生，本文设定木材AE信号的特征频率范围为45～47 kHz，即瞬时频率在此范围内，均视为发生了AE事件。虽然特征频率范围的设定将直接影响AE事件的数量，但是只要在同一个试验中保持同样的标准，对后继分析没有本质的影响，本文以频谱图中最大幅值的80%作为设定依据。

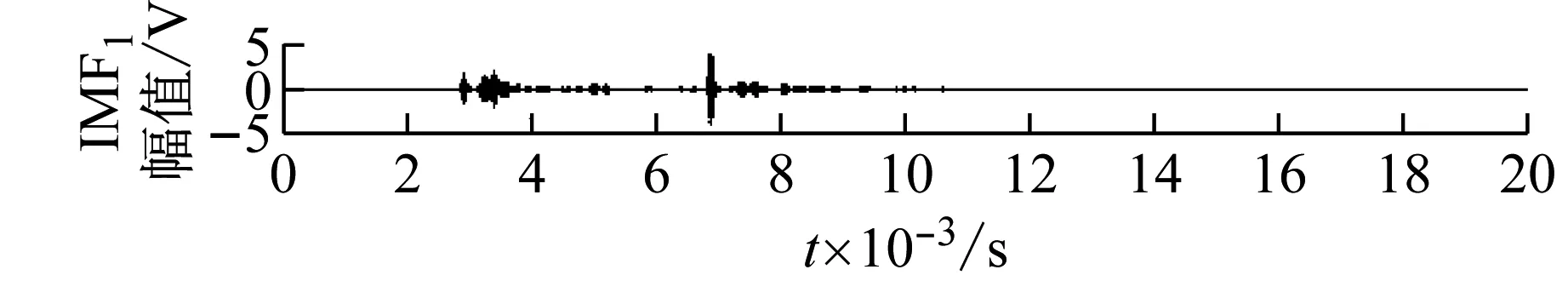
图6 EMD分解后的IMF分量及余项

在确定木材AE信号的特征频率范围后，就能够依据瞬时频率统计AE事件，图8是小波预处理后AE信号的IMF主分量的瞬时频率变化曲线，依据以上设定的特征频率范围，经统计在0.02 s的信号片段中，共发生了373次AE事件，显然，依据瞬时频率判断AE事件具有明确的物理意义。

(a) 频谱图(原始信号)

(b) 频谱图(原始AE信号IMF主分量)

(c) 频谱图(小波处理后AE信号的IMF主分量)

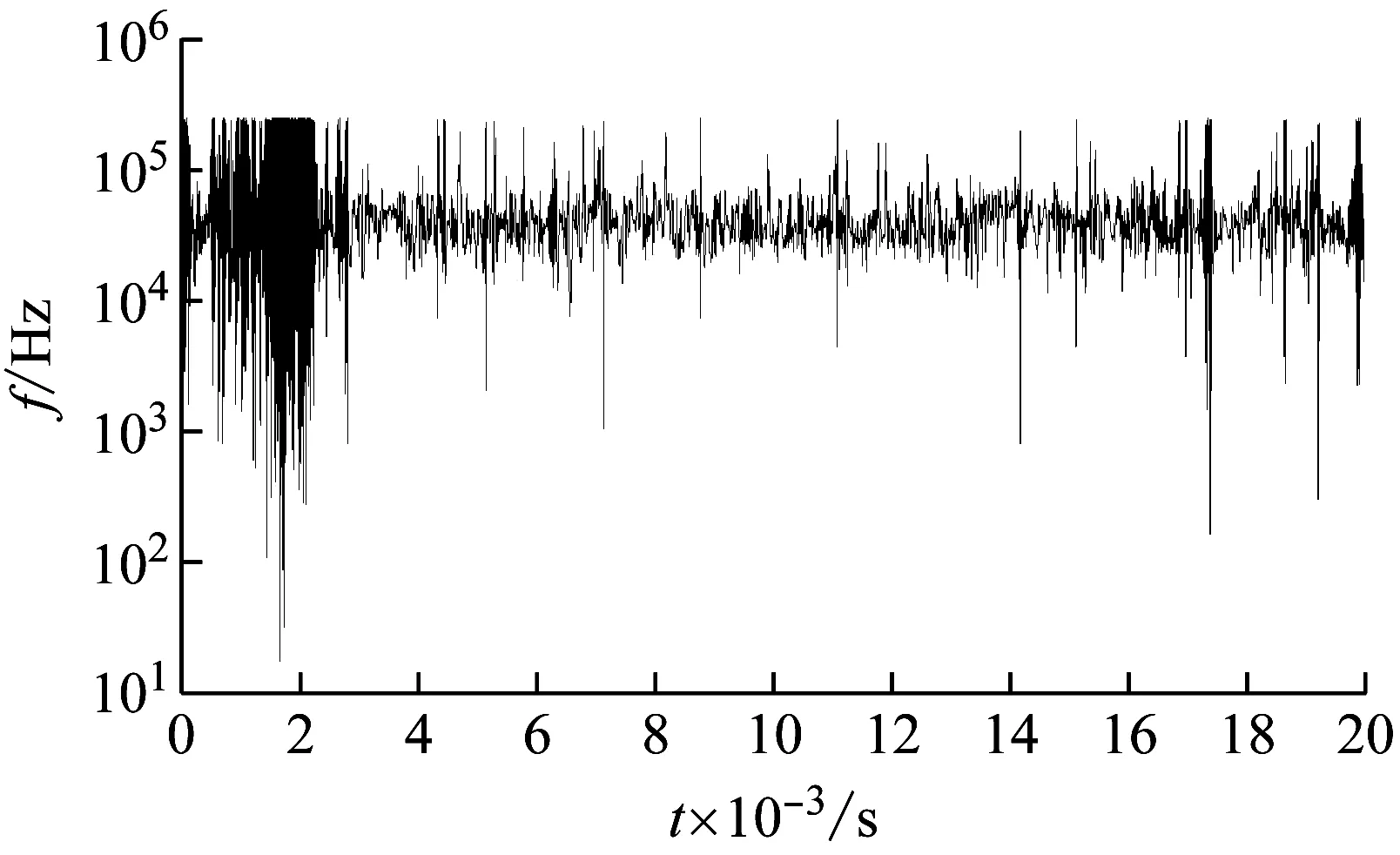
图8 IMF主分量的瞬时频率曲线

4 结 论

AE技术为木材损伤提供了有效的主动无损检测方法，受复杂的物理结构影响，木材AE信号呈现较强的非线性和非平稳性特征，为此，本文结合小波预处理和EMD分解相结合的方法，在降噪的同时提取木材AE信号的频率特征，并且从瞬时频率的角度判定AE事件的发生，使得AE事件的定义更具物理意义。

本文根据生成信号包络线的插值节点的极值性质，将插值节点处的一阶导数值为零增加为新的插值条件，从而形成改进的分段三阶Hermite插值拟合算法，不仅有效解决了三次样条插值容易出现过冲的现象，还有效避免了拟合误差的传播，从而提高包络拟合的精度，进而在IPCHI包络拟合的基础上提出改进的EMD算法。

其后以云南松试件为对象，通过三点弯曲试验获取木材损伤过程的AE信号，并截取0.02 s的信号片段进行分析，通过比较分析，AE信号经过小波预处理后，再进行EMD分解可以得到较为理想的IMF主分量，并且根据IMF主分量的频率分布容易确定木材AE信号的特征频率范围，最后利用瞬时频率判定并统计AE事件，从而为木材AE信号特征研究提供了一种有效的分析方法。

未来可以将本文提出的方法进一步推广到整个木材损伤过程，研究木材损伤程度与AE事件累积量之间的本构关系，从而建立基于AE特征的木材损伤预测本构模型。