基于Hyperworks的六边形蜂窝板铺层等效建模方法研究

2018-12-21王皓辉盛晓伟

振动与冲击 2018年23期

徐洋, 王皓辉, 盛晓伟

(东华大学机械工程学院，上海 201620)

蜂窝板特点是强度高、刚度高、质量轻、隔热性能好，且在受到高强度冲击载荷时其胞壁结构发生弹性和塑性变形的同时可吸收冲击能量，是一种具有良好力学特性的轻量化结构，因此被广泛地应用于航空航天结构等各个领域。在工程领域中，对于蜂窝板这样的复杂结构，通常是借助计算机利用有限元方法对结构进行分析，其优势是能够精确地处理复杂结构问题，但缺点是需要过多的时间成本。因此，如何快速高效的建立蜂窝板模型是分析结构特性的前提条件。

迄今为止，已经有很多学者研究了蜂窝板等效理论，如：Boudjemai等[1]利用了各向同性的整块板等效方法，方法虽可行实用，但却只能从宏观上描述其特性，无法从微观上进行有效分析——即无法反应蜂窝板蒙皮与蜂窝芯子之间的影响。董彦鹏等[2]提出了一种结构相似有限元模型等效方法，等效性得到了验证，但是建模过程仍然非常复杂，并没有得到有效简化。蔡园武等[3]提出了一种周期性板件刚度等效方法，但是其计算结果误差相对较大，只能在相对狭小的特定范围内才能使用。Allen[4]建立的蜂窝板模型忽略了面内刚度和弯曲刚度，虽然蜂窝芯层很软，但是对于蒙皮而言具有较大的厚度，所以忽略面内刚度和弯曲刚度必然导致明显的误差。Ha等[5-6]通过将蜂窝芯层视为服从剪切变形理论的正交异性层建立了分析模型，在部分领域内效果很好。Gisbon等[7-8]通过理论方法给出了蜂窝材料的等效参数公式，虽然其解析形式便于应用，但是也有缺点，在推导过程中仅仅只考虑了蜂窝板的弯曲变形，而没有考虑蜂窝胞元壁板的伸缩变形，因此其公式带有一定的误差。Xia等[9]将蜂窝板各种等效方法进行计算并将计算结果进行了比较，但是却没有具体介绍等效方法。

为了快速准确分析蜂窝板材力学特性，本文提出了一种基于Hypermesh的铺层等效有限元建模方法，其计算结果与目前常用有限元建模方法比较可知，该方法具有更高的效率且准确可靠。

1 蜂窝板的建模方法

1.1 蜂窝板结构介绍

在大多数工程应用中，蜂窝板是由上、下蒙皮和中间的蜂窝芯子构成，蒙皮与芯子采用黏结剂进行连接。通常六边形单胞构成的周期性板是用来作为蜂窝板芯层，具体结构，如图1所示。

图1 蜂窝板结构示意图

1.2 蜂窝板常用建模方法

目前，蜂窝板的有限元建模方法大致可分为两种[10-11]：全实体建模方法和等效板建模方法。

(1) 全实体建模：其本质是将蜂窝板按照实体模型建模，蒙皮、芯子等全部构建，如图2所示。

图2 蜂窝板全实体建模

该方法对于单块的蜂窝板件研究可以达到不错的效果与精度，但是在实际工程应用中，这样的建模方法所耗费的计算资源与时间成本非常巨大。

(2) 等效板的建模：是目前使用最为广泛的方法，其特点是将蜂窝板等效为一块连续的各向同性/异性的板件，如图3所示。

等效板建模虽然可以节省计算成本与时间，但在计算精度方面随着阶数的增加误差会越来越明显。另外，使用等效板方法建模只能得到宏观的力学响应结果，对于板件内部的微观性能是无法得到的(比如蒙皮与芯子的相互作用)，通常需要设计师的经验才能进行判断。

图3 等效板结构示意图

1.3 蜂窝板铺层等效有限元模型建模

本文在前两种建模方法的基础上提出了铺层等效有限元模型建模方法。其原理是：通过材料铺层将蜂窝板等效为一种铺层性质的材料。不仅能实现层与层的共节点，而且还可以输出层与层之间的响应，如图4所示。同时在分析过程中将胞壁纵向受载时的伸缩变形考虑在内，使得结果更为精确。

图4 铺层等效示意图

建立如图5所示的理论模型，考虑蜂窝材料在横向受载时的材料性质，假设等效后的匀质材料为均匀的单项拉伸状态(见图6)，可得

(1)

P=σ1(H+Lsinθ)b

(2)

式中：b为壁板宽度，通过弯曲理论，AB的挠度是

(3)

(4)

等效应变为

(5)

(6)

等效泊松比μ1为

(7)

通过式(2)和式(5)可得横向杨氏模量为

(8)

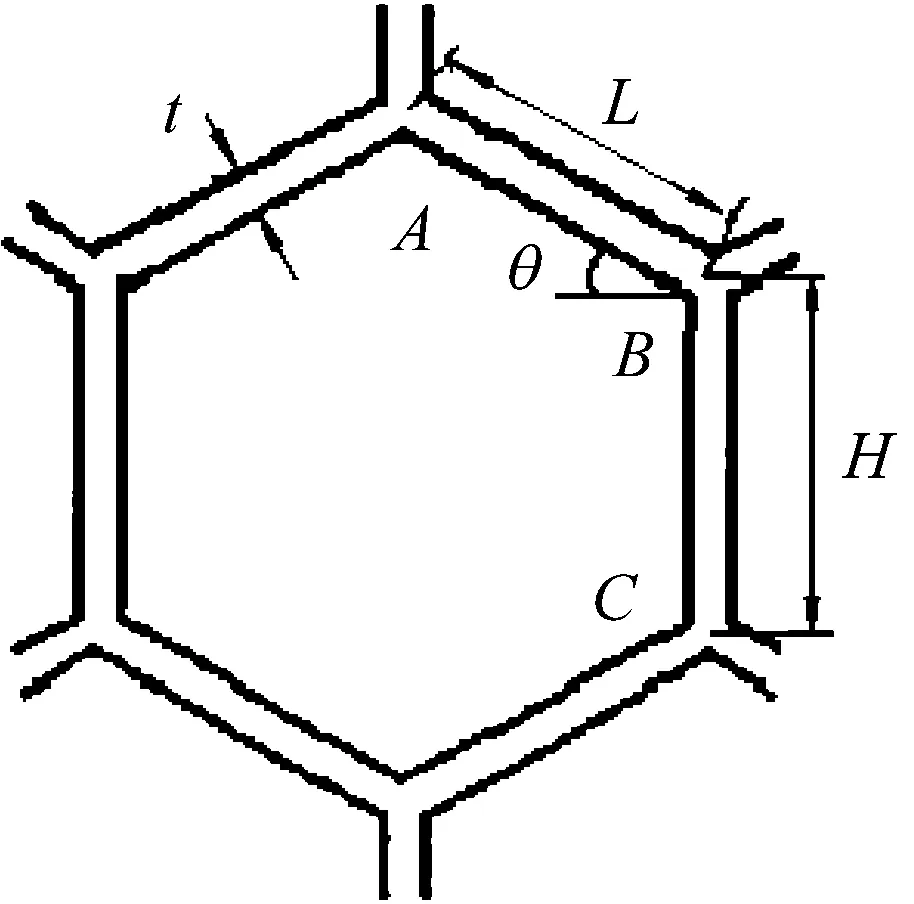
图5 蜂窝胞元

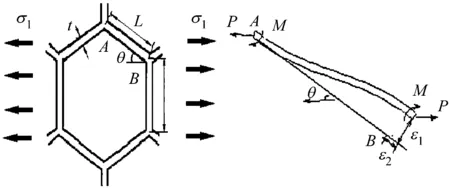
图6 蜂窝胞元的横向变形

对于纵向受载时的力学特性分析(见图7)，同样假设等效后的匀质材料为均匀的单项受力状态，与横向受载不同的是将BC段的伸缩变形考虑在内，因此可得

(9)

W=Lσ2sinθ

(10)

由弯曲理论AB的挠度为

(11)

负载W引起壁板AB的伸长量为

(12)

BC的伸长量为

(13)

等效应变为

(14)

(15)

等效泊松比μ2为

(16)

则纵向杨氏模量为

(17)

图7 蜂窝胞元的纵向变形(考虑伸缩变形)

因此蜂窝材料参数为

(18)

对于a≪1，可以有近似公式

(19)

在公式中可以注意到t2/L2是很小的，湖忽略高阶无穷小量o(t2/L2)。对于正六边形H=L,θ=π/6，式(18)可以简化为

(20)

考虑蜂窝胞元壁板(BC段)的伸缩变形对于高精度工程应用领域(如精编纺织机械、航天卫星部分结构等)效果比较明显，因为这类设备通常前几阶模态以伸缩扭转为主，而对于其他大型工程应用领域(如工程机械、海洋平台等)计算结果区别并不明显。

将等效参数输入铺层等效模型中，获得的计算结果相比于用实体网格建模的全实体建模方法，该方法计算规模得到大幅缩减。而相比于同样采用Shell单元建模的等效板建模方法，该方法可使层与层之间的响应输出，准确性得到极大提高。蜂窝材料的铺层等效有限元模型构建方法能够反应板件的宏观、微观力学特性，但由于蜂窝芯层的等效层与原六边形芯层有差异，因而不适用于胞元的微观变形分析。

2 具体算例

以某卫星的一块长方形承重板为例进行计算。文中为证明铺层等效有限元法效果，依据“全实体建模的蜂窝板与实际蜂窝板有极高的一致性”结论，特将蜂窝板全实体有限元模型计算结果作为进行比较的基准[12-14]。

该板具体示意图，如图8所示。长为250 mm，宽为200 mm，蜂窝板总厚度为15 mm，上下蒙皮厚度均为0.3 mm，正六边形铝制蜂窝胞元厚度为0.04 mm，边长为4 mm。材料弹性模量72 GPa，密度2.8×103kg/m3，泊松比为0.3。

约束条件分别如下：

在计算模态时，AB与A1B1固支；

计算静力分析时，A，B，C，D与A1，B1，C1，D1固定；

计算冲击时A，B，C，D与A1，B1，C1，D1为载荷加载点。

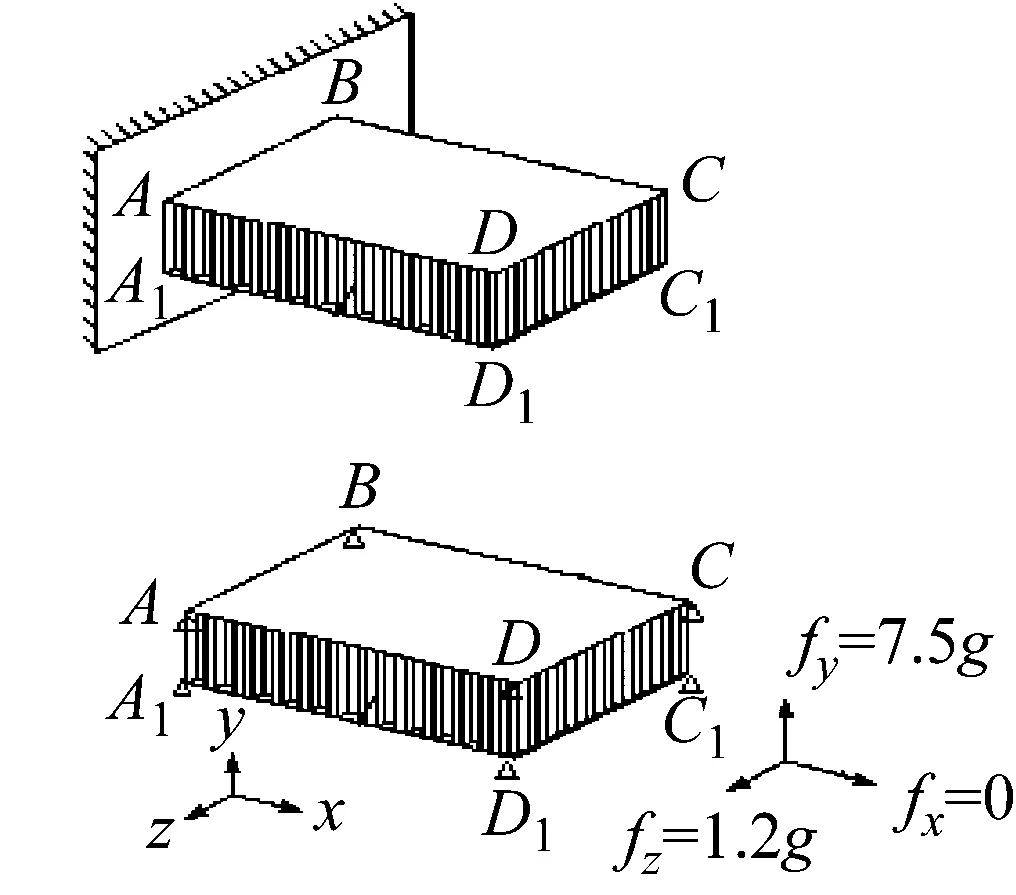
图8 算例示意图

2.1 固有频率计算结果

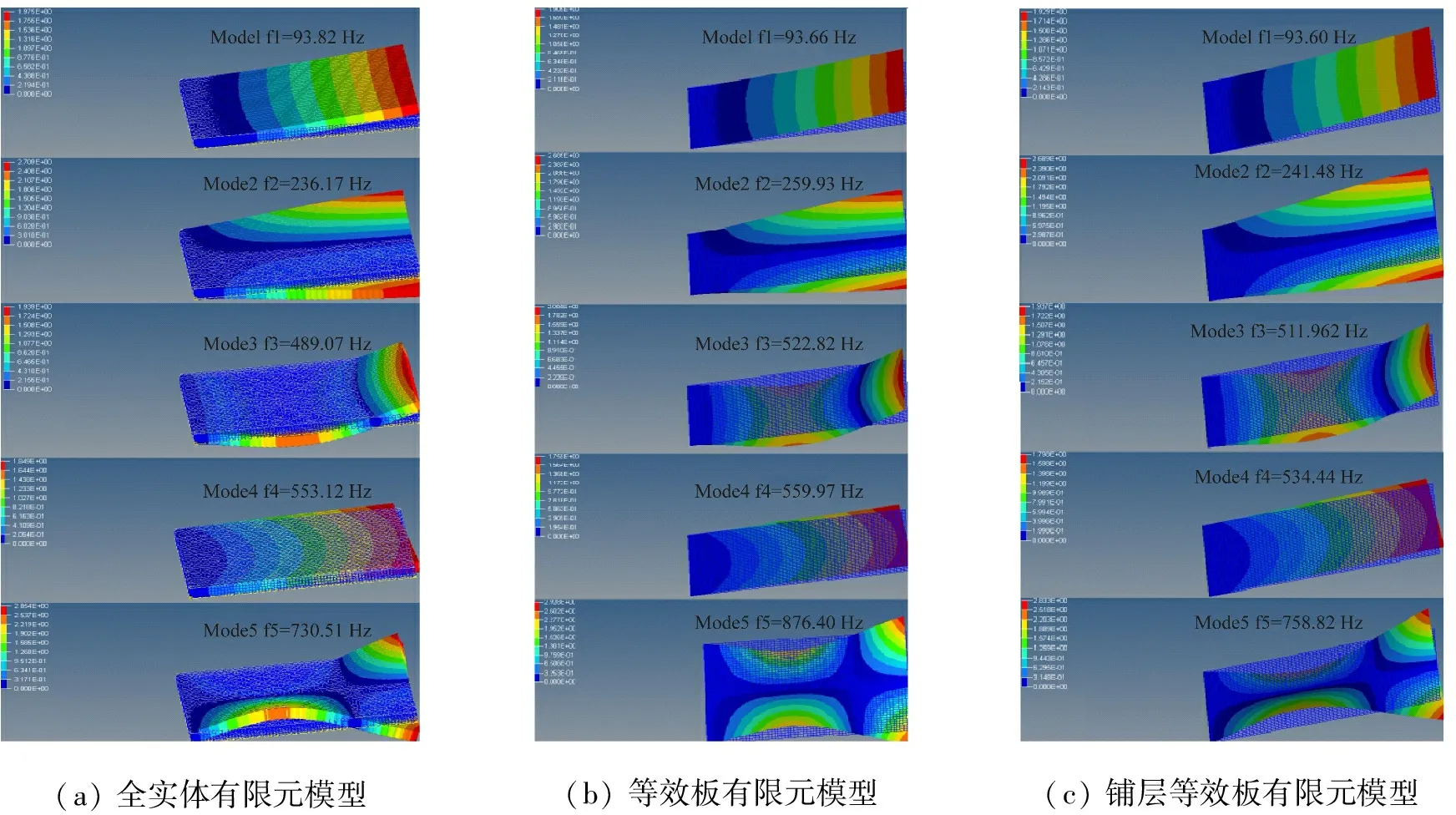
经计算，可得蜂窝板固有频率计算结果，如表1所示。模型前5阶振型图，如图9所示。

分析图9与表1可知，三种方法获得的前5阶振型基本一致。但铺层等效法的第1、第2、第4、第5阶误差明显要小于等效板(<5%)，第3阶模态误差有所增加，近5%。其误差来自于两个方面：①忽略胶黏层所带来的影响增大；②由来自于壳单元与上、下蒙皮夹紧系统引起差异的边界条件。此外，随着频率段的增大，误差会逐渐明显。为了更进一步体现误差，在0～5 000 Hz范围内将计算结果进行比较，如图10所示。从图10可知，铺层等效模型的计算结果是更加可靠。

表1 前5阶固有频率

2.2 静力计算结果

(1)位移计算

选择板的中心点作为位移参考点，(载荷为Fy=7.5g、Fz=1.2g)具体结果见表2。

分析表2的数据可知铺层等效模型的计算结果相较于等效板精度有明显提高，最大误差为-3.1%，而等效板误差最大达到6.25%。

(2) 应力计算

选择板的中心作为应力参考点，具体结果见表3。

分析表3的数据可知铺层等效模型的计算结果相较于等效板精度有明显提高，但是由于等效过程中边界条件的差异，绝对误差仍达到了5.3%。

2.3 冲击谱计算结果

冲击响应分析属于峰值类的分析，一般只关注响应的峰值是多少，所以设置的工况大多为极限工况，主要关注变化趋势，其结果相当保守。本算例冲击加速度响应谱为100～1 500 Hz是80g，1 500～5 000 Hz是2 000g，加载方向是y方向。分析比较板的最大位移轮廓以及应力分布云图，如图11、图12所示。

从图中分析可知，面板的变形特性稍有差别，靠近夹层结构边缘处的位移偏差有所增加，原因是结构边缘主要反应为蜂窝材料胞元的局部结构特性对面板的影响。但是面板变形的总体一致性较好。应力分布基本能够相互对应，在极限载荷工况下的冲击响应，应力的大小不关注。另外，冲击响应是运用模态叠加法进行计算的，在高阶频段下模态频率的误差会越来越明显，这样的影响在冲击响应中会进一步体现[15]。

(a) 全实体有限元模型(b) 等效板有限元模型(c) 铺层等效板有限元模型

图9 前五阶振型图

Fig.9 Various shape modes

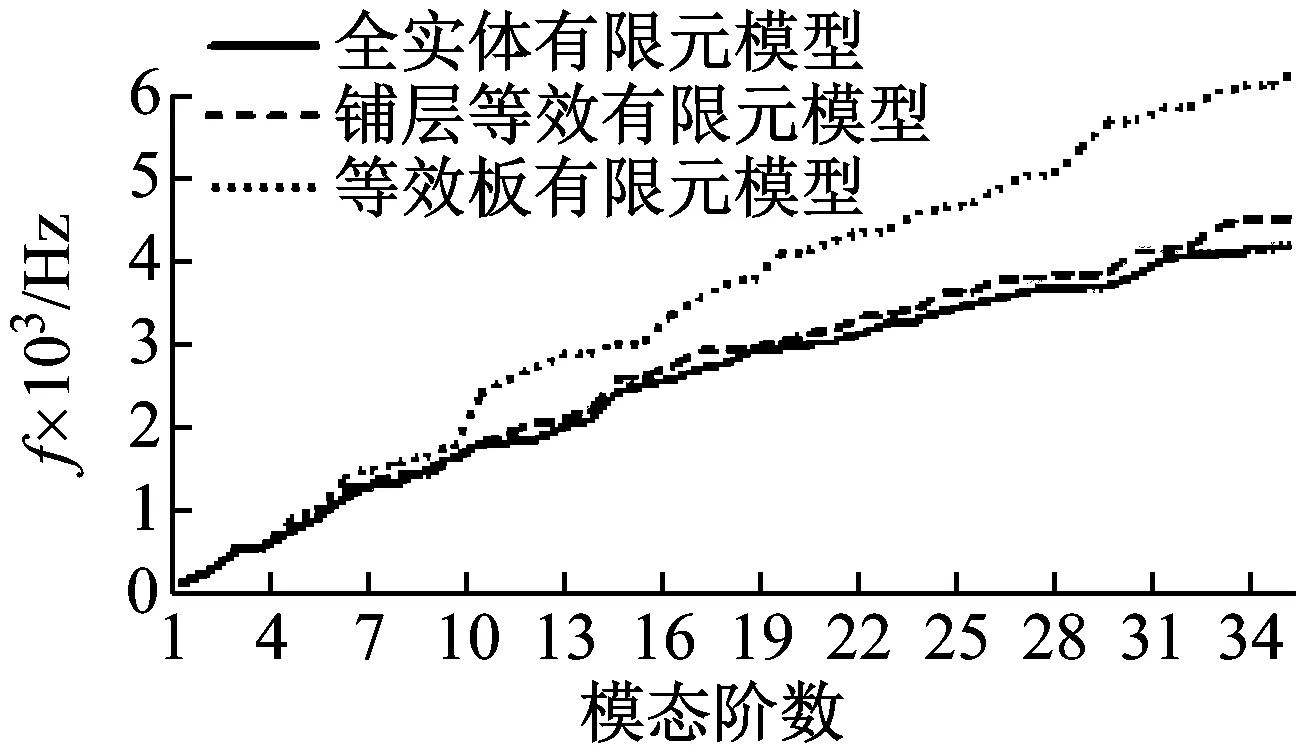
图10 结果对比图

参数/mm方法全实体蜂窝板等效板铺层等效板Y方向0.033 890.035 130.033 15Z方向0.000 480.000 510.000 465 1Mag方向0.033 910.035 140.033 16最大误差/%--6.25-3.1

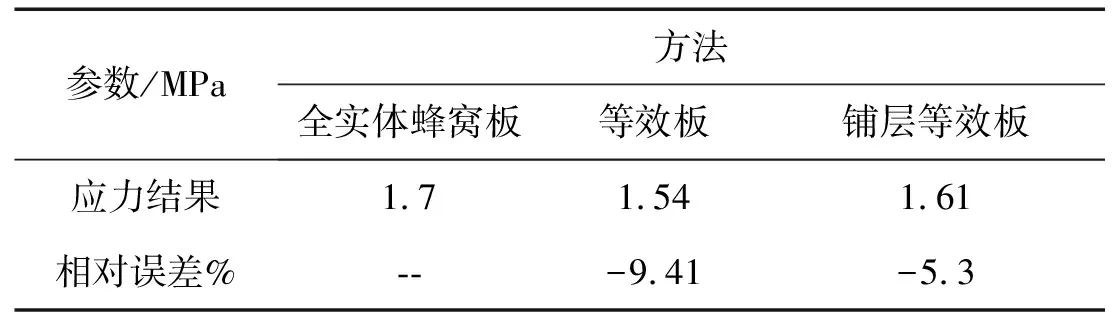
表3 应力计算结果

3 胞元尺寸与固有频率函数关系

对于蜂窝板这类的多孔板材，其均匀程度对板件的力学性能有着重要的影响，需要保证足够多的胞元数量以满足均匀性要求。而胞元尺寸对胞元数量有着决定性影响[16]。目前大部分有关于蜂窝板优化方面的文献很少有将胞元尺寸作为参数变量。其原因是胞元尺寸作为参数有其特殊性，与一般的形状变量不同，胞元尺寸的每一次改变都会牵涉到蜂窝芯子的重新布局，相当于每一次迭代都需要重新建模[17-18]。现有的有限元分析软件很难做到这一点[19-20]。

(a) 全实体有限元模型(b) 等效板有限元模型

基于铺层等效有限元模型，将铺层等效有限元模型的材料参数作为变量，由文献[9]可知等效参数公式是线性可逆的，胞元尺寸的每一次变化都会带动铺层板材料参数的变化，由此可以间接的知道胞元尺寸与固有频率之间的关系，为今后的蜂窝板优化提供了参考依据。

频率与多参数方程可以简单地表示为

fi=f(h,l,t,tcell)i=1，2，3，4，5

(21)

(a) 全实体有限元模型(b) 等效板有限元模型

图12 冲击响应应力云图

Fig.12 Stress of shock response

式中：h为蜂窝芯子高度；l为胞元尺寸；t为蒙皮厚度；tcell为胞元厚度。

对式(21)进行全微分得到如下方程

(22)

式(22)可以近似地表达为

(23)

式(23)为蜂窝板固有频率的变化是由蜂窝板内部其中一个或多个参数变化的结果。本次仅针对胞元尺寸与固有频率的关系，因此，保持其他参数不变，而胞元尺寸从l=1 mm到l=10.5 mm每隔0.5 mm取点进行计算，总共选取20个点，将计算结果导入MATLAB画出关系图并拟合出函数，如表4与图13。

图13 胞元厚度与频率关系图

参数常数项的确定依赖于一定区域范围内参数与频率的关系式，对于同一范围内的数据点可能不止一种函数关系表达式，但是这些函数表达式在这一区域所表达的参数意义是相同的，因此在确定参数范围所导出的数据点以拟合的方程中只需要选择形式简便连续性好的方程即多项式形式。

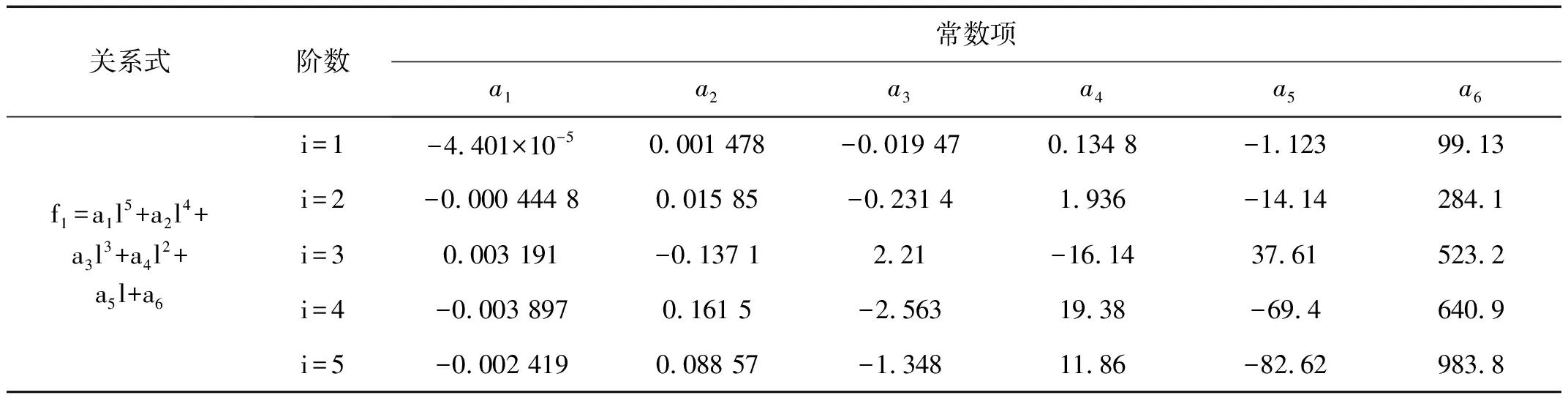
表4 函数关系

根据图13的计算结果可知在胞元尺寸增大的情况下，第1、第2阶固有频率变化并不明显，从第3阶开始，固有频率的变化逐渐增大，第5阶固有频率初始变化最明显，但是随着尺寸的增大逐渐趋于平稳。总体而言，胞元尺寸对第3、第4、第5阶的固有频率影响要大于对第1、第2阶固有频率的影响[21-24]，主要原因有两方面：①对于有限元模型，网格划分对计算频率结果较敏感，因此不同的网格划分方法会直接影响到计算频率；②第1、第2阶模态主要以弯曲变形为主，而第3、第4、第5阶模态则以伸缩、扭转为主，由前文分析考虑了蜂窝伸缩变形使得结果更精确，所以对于以伸缩、扭转为主的第3、第4、第5阶模态影响更大。