旋转机械一维深度卷积神经网络故障诊断研究

2018-12-21周奇才刘星辰沈鹤鸿熊肖磊

振动与冲击 2018年23期

周奇才，刘星辰，赵炯，沈鹤鸿，熊肖磊

(同济大学机械与能源工程学院，上海 201804)

随着机械设备复杂度和可靠性要求日益提高，其维护方式由传统的事后维护和定期维护转向更加高效的基于状态维护(Condition-Based Maintenance, CBM)。CBM的思想是利用获取的设备信息，通过状态监测、故障诊断和寿命预测，在有证据表明发生故障或即将发生故障的情况下对设备进行维护[1]。旋转机械是机械设备的关键组成部分，从整体上说，机械设备的绝大多数机械故障，都与回转部件有着直接或间接的关系[2]，因此，旋转机械基于状态维护研究是提升机械设备维护水平的关键。

近年来，人工智能诊断——人工神经网络、支持向量机、隐马尔可夫链等方法由于强大的数据处理和故障自动识别能力，在旋转机械状态维护领域得到广泛应用。这些诊断方法通常包含两个步骤：基于信号处理的特征提取和基于分类模型的健康状态识别。文献[3]利用主成分分析(PCA)提取故障特征并通过该相关向量机和支持向量机实现轴承故障识别。文献[4]对原始信号进行功率谱、倒谱和高阶谱分析，并结合三层人工神经网络识别感应电机故障。文献[5]利用经验模态分解提取时域特征，并通过优化后的BP神经网络实现故障识别；文献[6]提取振动信号时域、频域和时频特征，在此基础上利用动态主成分分析(DPCA)选取有效特征，最后通过隐马尔可夫的马氏距离模型实现健康状态评估。在文献提出的智能诊断方法中，人工神经网络由于自适应和拟合能力强等优点，在旋转机械故障诊断中成为应用最为广泛的方法之一。然而当前应用的人工神经网络模型存在以下缺陷：①输入人工神经网络的特征向量需要通过信号处理的方式人工提取，不仅需要专家知识和经验，而且由于提取的特征针对特定的问题，导致训练的模型推广性差；②目前人工神经网络由于梯度消失和梯度爆炸等问题，一般采用3～4层的浅层网络结构[7-8]导致网络非线性拟合能力差，难以满足复杂机械系统的诊断精度和鲁棒性要求。而深度学习，包括卷积神经网络(CNN)，循环神经网络(RNN),深度信念网(DBN)和深度自编码器(DAE)等模型由于较深的网络结构，兼具复杂的特征学习和分类能力，是解决上述问题的有力工具。

深度学习(Deep Learning, DL)理论自从Hinton等[9]提出无监督逐层训练结合有监督微调方法后，成为机器学习和人工智能领域研究的热点。和传统智能诊断模型相比，深度学习因其多层网络结构在自适应特征学习和表示方面有强大的能力，并且在机械状态监测领域得到广泛应用[10-11]。文献[12]利用信号时域、频域和小波域混合特征，结合3层堆叠稀疏自编码器和softmax回归，实现轴承故障诊断。文献[13]利用信号频域信息，结合三层堆叠自编码器和softmax回归，实现轴承和行星齿轮箱的故障诊断。文献[14]利用堆叠自编码器实现齿轮箱和电力机车滚子轴承的诊断，并通过人工鱼群算法优化模型参数。上述研究虽然在故障诊断中应用深度学习模型，但是仍然采用人工提取特征作为输入，没有发挥深度模型特征学习的特性。

卷积神经网络(CNN)作为经典的深度学习模型，其独有的卷积结构具备强大的特征学习能力，在图像识别领域取得巨大的成功，从2012年开始,不断提出新的卷积神经网络，AlexNet[15]、GoogleNet[16]和ResNet[17]等,垄断了ImageNet图像识别大赛上的冠军，同时在机械状态监测领域也有广泛的应用。文献[18]提出一种将时域信号转换成二维图像的方法，并结合改进LeNet5模型实现轴承和离心泵的故障诊断。文献[19]利用电机电流信号，结合改进的一维卷积神经网络实现电机实时监测，由于模型深度小，结构简单，仅用于电机状态二分类问题，并且诊断精度不高(97.4%)。文献[20]结合原始信号Droupout机制和一维卷积神经网络，实现了噪声信号下的故障诊断。文献[21]采用单层卷积层结合全连接神经网络模型，实现轴承的故障诊断，同样由于深度较浅，模型的诊断精度不高(93.61)。文献[22]利用单卷积层和池化层结合全连接层实现齿轮故障的诊断。

在现阶段卷积神经网络的发展中，AlexNet起到里程碑式的作用，其深度的结构和思想是后续新卷积神经网络不断提出的基础。本文在经典卷积神经网络AlexNet的基础上，为适应时域信号的处理，提出基于一维深度卷积神经网络故障诊断模型(1D Convolutional Neural Network Diagnosis model,CNNDM-1D)。模型由多个交替的一维卷积层和池化层形成深度卷积网络，完成原始信号的特征自适应学习，并结合全连接层实现故障分类。本文剩余内容安排如下：第一小节将对卷积神经网络和AlexNet结构及相关理论作简要介绍；第二小节提出基于一维深度卷积神经网络的故障特征提取和诊断模型；第三小节利用轴承和齿轮箱健康状态监测数据对提出模型进行验证，并和典型的诊断模型作对比。第四小节对本文研究和实验结果进行讨论和总结。

1 卷积神经网络和AlexNet

本节首先介绍卷积神经网络基本结构和相关理论，然后介绍经典卷积神经网络AlexNet结构。

1.1 卷积神经网络

卷积神经网络是一种典型的前馈神经网络，其提出旨在模拟哺乳动物视觉皮层的结构和功能。卷积神经网络包含卷积(filter)和分类(classification)两阶段结构，卷积网络主要包含卷积层和池化层，实现输入数据的特征自学习，分类网络主要包含全连接层和分类器。

1.1.1 卷积层运算

卷积层运算通过卷积核(filter kernel)对输入数据进行卷积操作，卷积的结果即是提取的特征。通常一个卷积层有多个卷积核，由于同一个卷积核在卷积的过程中共享参数，因此一个卷积核学习得到一类特征，称为映射图(feature map)。卷积运算的过程如式(1)所示

i=1,2,…，q

(1)

其中i代表第i个卷积核，g(i)代表第i个卷积核学习得到的映射图，a代表输入数据，b代表卷积核的偏置。x,y,z代表输入数据的维度，对于图像而言，x和y代表长度和宽度方向的像素大小，z代表图像通道数。对于一维时域信号，只需对后两个维度进行简化即可。

在完成卷积运算后，通过激活函数进行非线性变换。卷积层通常采用Relu激活函数，如式(2)所示

y(i)=f(g(i))=max{0,g(i)}i=1,2,…，q

(2)

1.1.2 池化层运算

池化层通池化核对输入数据进行子采样(subsampling)，在实现数据降维的同时提取特征。池化包含最大池化和平均池化，其中最大池化效果最佳，应用广泛，其运算如式(3)所示

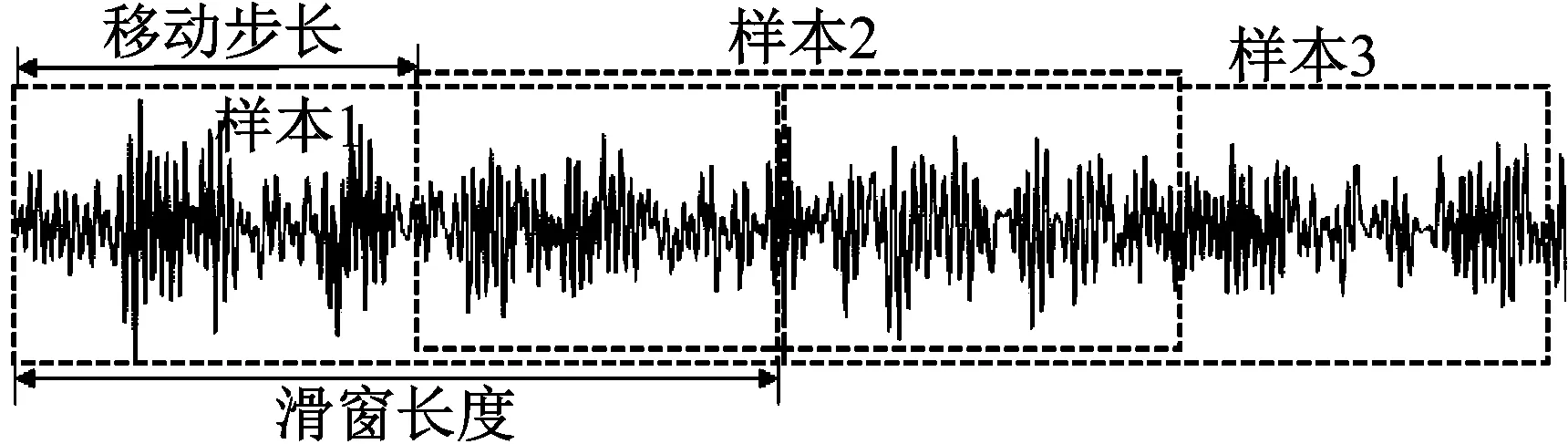
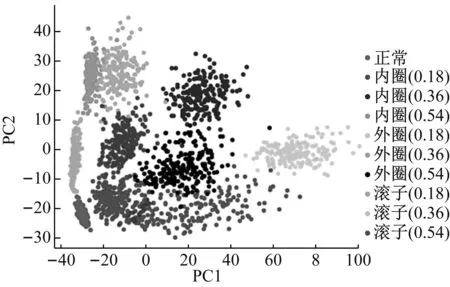
pl(i,j)=max(j-1)w

(3)

其中al(i,t)代表第l层中，第i个映射图(feature map)的第t个神经元。W代表卷积核的宽度，j代表第j个池化核。

1.2 AlexNet

AlexNet是Alex Krizhevsky于2012年提出的深度卷积神经网络模型，相比前辈LeNet-5网络[23]，其深度大大增加，共包含5层卷积层、3层池化层、2层局部响应归一化层(Local Response Norm, LRN)和3层全连接层，除深度增加外，模型首次使用Relu激活函数，Dropout和LRN等方法，使卷积神经网络在特征学习上取得巨大的突破，为后续的VGGNet、GoogleNet等卷积神经网络奠定了基础。

由于卷积神经网络随着深度的增加将使训练样本数量和计算量呈指数增长，因此当前卷积神经网络在机械设备故障诊断领域一般基于LeNet5等较浅的卷积神经网络，而Simonyan等指出，卷积神经网络越深，其特征学习和分类效果越好。作者认为，机械设备状态监测样本获取并不困难，并且可以通过数据增强技术来增加样本[24]，同时计算能力也随着显卡的应用不再成为瓶颈。接下来本文将提出基于AlexNet的一维深度卷积神经网络，通过实验验证模型效果，并对以上两个问题加以说明。

2 一维深度卷积神经网络

本节提出基于一维深度卷积神经网络的特征学习和故障诊断模型CNNDM-1D，模型通过多个交替的卷积层和池化层完成自适应特征学习，并结合全连接层实现故障诊断，同时本节将对样本构造和模型训练过程进行说明。

2.1 CNNDM-1D结构

CNNDM-1D结构如图1所示，包含5个卷积层，3个最大化池化层和3个全连接层，其中1×20s3-16表示卷积核的尺寸为1×20,移动步长为3，深度为16。和经典AlexNet相比，其针对时域信号主要改进如下：

(1) 采用一维的卷积核和池化核，以适用于一维振动时序信号。对于一维时域信号，采用一维卷积和池化可以保证原始信号的直接处理，而不需对原始信号进行二维转换，减少了信号预处理的工作量。

(2) 前几层卷积层采用较大尺寸的卷积核，以提取大尺度下的时域信号特征，卷积核的尺寸随深度增加而减小。

(3) 去除LRN层，LRN层是一种正则化手段，它被指出对诊断精度影响不大，同时它的存在将大大降低训练速度(3倍)。本文提出模型将采用L2正则化。

图1 CNNDM-1D 结构

2.2 样本构造

模型的输入为原始振动信号，考虑到模型的深度结构需要较多的训练样本，本文采用滑窗的方式截取训练和测试样本。如图2所示，滑窗长度即为截取的样本长度，移动步长为滑窗一次移动的距离，通常小于滑窗长度，因此两个相邻样本间有部分重叠。

在本文中，滑窗长度为2 000，移动步长为1 000，采用这种滑窗样本构造方式将使样本数量增加一倍，同时可以避免样本的截断导致特征丢失。

图2 滑窗样本构造

2.3 模型构建

CNNDM-1D模型的构建分为两大部分：模型的训练和测试。模型训练首先建立2.1节所述网络结构，网络输入层单元数等于样本维数，输出层单元数等于诊断对象健康状态数。建立网络结构之后，对训练参数进行初始化，在接下来的实验中，训练参数设置如下：网络权重的初始值利用Xavier函数[25]设置，偏置设为0；学习率通过指数衰减法设置,初始学习率为0.035，衰减率为0.99；对全连接层设置Dropout和L2正则防止过拟合，其系数分别为0.5和0.000 1；模型共进行3 000轮训练，每次训练输入100个样本，样本从训练集中随机抽取。模型运行的软件环境为:Python+Tensorflow;硬件环境为:Intel i7-5820K+Nvidia 1080ti。

模型训练在达到最大训练轮数后结束，将测试集输入训练好的模型，对比模型预测的标签和真实标签，从而模型的诊断精度和稳定性。模型的构建流程如图3所示。

图3 CNNDM-1D构建流程图

3 旋转机械健康状态监测实验

旋转机械健康状态监测实验对象为轴承和齿轮箱。实验台如图4所示，从左至右依次为电机、齿轮箱、三个轴承和磁粉制动器。其中齿轮箱为二级齿轮箱，轴承为单列滚子轴承(N205),轴承2处可以通过螺旋机构给三个轴承施加径向载荷，磁粉制动器施加轴向载荷。轴承和齿轮箱的详细参数，如表1所示。

图4 旋转机械故障实验台

参数数值轴承节圆直径/mm38.5滚子直径/mm6.5滚子数13齿轮箱齿轮模数/mm2齿宽/mm20压力角/(°)20主动/从动齿轮齿数55/75齿轮间隙/mm0.5

3.1 轴承故障诊断实验

轴承故障诊断对象为轴承3，在实验过程中，径向载荷和轴向载荷均设为0,电机转速保持1 500 r/min。振动数据通过安装在轴承座竖直径向上的传感器(YD-186)获取，采集频率设为20 480 Hz。轴承的状态共分四种：①正常；②内圈故障；③外圈故障；④滚子故障。其中每一种故障状态各包含宽度为0.18 mm、0.36 mm和0.54 mm三种程度的故障，深度均为0.1 mm,故障通过切割方式加工，呈沟槽状。实验共进行1O次，每次实验进行20 min，结束后更换相应的故障轴承。

对应10种轴承状态，每种状态取2 000个样本，故样本集共含20 000个样本。采用10折交叉验证方法划分数据集，利用分层采样划分10个等分子集，每次9个子集用于训练，1个子集用于测试，如表2所示。每个样本包含2 000个数据点，相应的CNNDM-1D输入层神经元数为2 000，输出层神经元数为10。样本的输入维度是模型诊断精度的重要影响因素之一，作者通过实验发现，输入维度增加，诊断精度随之提高的同时模型训练变慢。输入维度设为2 000是在保证足够高诊断精度和较快的训练速度条件下的选择，以适应一些实时性要求高的应用场景。

表2 轴承数据集

3.1.1 实验结果

10折交叉验证共进行10次训练，训练完成后分别用训练样本和测试样本检测模型的诊断精度，分别为训练精度和测试精度。训练和测试共进行30次，结果如图5所示。模型训练精度均为100%，测试精度均在99.76%以上，平均精度为99.80%，标准差为0.024%。实验结果表明，本文提出模型可以精确诊断轴承健康状态，同时诊断鲁棒性较好。模型训练平均用时为68.6 s,测试为0.12 s，可见模型诊断实时性较好，可以用于计算能力较差的嵌入式设备。

图5 轴承故障诊断实验结果

3.1.2 模型参数优化

在本文模型的优化过程中，有两个参数的设置对最终诊断精度影响较大：第一层卷积层卷积核尺寸和第二层全连接层单元数。首先，不同卷积核尺寸对诊断的精度如表3所示。由表3可知，第一层卷积层宜采用较大尺寸的卷积核，但是当尺寸大于20×1时，模型精度不再上升甚至稍有下降，从减少参数和过拟合的角度，20×1的尺寸是较优的选择。

表3 卷积核尺寸对诊断精度的影响

第二层全连接层单元数对模型诊断精度影响如表4所示。由表4可知，单元数宜设置在100以上。当大于200时，精度不再上升甚至稍有下降，综合考虑诊断精度和计算开销，单元数设为100是较优的选择。

表4 全连接层单元数对诊断精度的影响

3.1.3 模型对比

基于LeNet5的一维卷积神经网络(LENET5-1D)、经典AlexNet、支持向量机(SVM)和BP神经网络用于和本文提出模型作对比。其中AlexNet的输入维度为45×45，卷积核和池化核不作改进。LENET5-1D包含两层卷积层、两层池化层和两层全连接层。卷积核大小分别为1×11和1×7,深度分别为6和16，步长均为1。池化核大小为1×2，移动步长为2，卷积核和池化核均采用全零填充；SVM模型采用高斯核函数；BP神经网络输入层、隐层和输出层单元数分别为1 000、500、10，激活函数为sigmoid函数。模型诊断对比结果如表5所示。

表5 本文模型和其它模型对比

从诊断结果可以看出，本文提出模型相比经典AlexNet模型，在诊断精度上有较大的提升，证明改进的一维卷积模型更适合时域信号的处理。相比典型的浅层模型SVM和BP神经网络，在诊断精度和稳定性上均有较大优势，其原因在于浅层模型特征学习能力有限，学习到的特征不具备较好的分类特性。

相比同类型的LENET5-1D模型，其诊断精度和稳定性均有一定的提升。同时在样本较少的情况下，CNNDM-1D较LENET-1D优势更为明显，当样本集数量降至2 000时，CNNDM-1D的诊断精度为99.5%，而LENET5-1D的诊断精度降至96.8%，说明深度的增加对模型的特征提取能力和诊断能力有较大的提升。

3.1.4 特征学习验证

为了验证模型对原始输入信号的特征学习能力，利用主成分分析(Principal Components Analysis, PCA)对模型倒数第二层全连接层学习到的特征进行分析和可视化。如图6所示，模型学习到各状态下的特征分离度很高，具备很好的分类性能，由此可见，模型可以从输入的原始信号中提取有效的特征。

图6 学习特征PCA分析

3.2 齿轮箱故障诊断实验

对应5种齿轮状态，每种状态取2 000个样本，故样本集共含10 000个样本。采用10折交叉验证方法划分数据集，利用分层采样划分10个等分子集。样本维度同样设为2 000。

3.2.1 实验结果

10折交叉验证同样进行10次训练和测试，结果如图7所示：模型训练精度均为100%，测试精度均在99.9%以上，平均精度为99.95%，标准差为0.025%。实验结果表明，本文提出模型可以精确诊断齿轮健康状态，同时诊断鲁棒性较好。模型训练平均用时为75.6 s,测试为0.05 s。

3.2.2 模型对比

用于对比的模型同轴承故障诊断实验，实验结果如表6所示，结果表明本文提出模型较经典AlexNet、典型浅层模型SVM、BP神经网络诊断精度和稳定性上均有明显提升。同时相比同类浅层模型LENET5-1D，其精度提升0.8%，较轴承故障诊断实验的差距小，这主要是因为齿轮箱故障类别较少，分类难度也较前者小，因此即使是较浅的一维卷积神经网络也能取得较好的效果。当样本数量降至1 000时，本文模型仍能达到99.6%的精度，而LENET5-1D则降至97.2%。