内输多相流与绕流耦合作用下立管非线性振动
2018-12-21马天麒顾继俊张赢今李明婕
马天麒, 顾继俊, 孙 旭, 张赢今, 李明婕
(1. 复旦大学 航空航天系,上海 200433; 2. 中国石油大学(北京) 机械工程学院,北京 102200; 3. 德州学院 机电工程学院,山东 德州 253023)
深水油气立管系统是油气开发系统中重要的部件,立管具有多种结构,如顶部张紧力立管(TTR),自由悬链线立管(SCR)、混合立管等。 深水顶部张紧力立管主要有钻井立管,生产立管,注水管等。虽然立管的用途不同,但立管的组成结构基本相同。由于TLP和Spar平台的垂荡运动较小,因此TTR立管多用在TLP和Spar平台中。TTR区别于SCR是需要足够顶张力来保持立管垂直。立管在海洋环境中会受到风、浪、流、管内流体以及立管两端作用力的影响。流体流动会引起立管振动(FIV),包括内输轴向流体所引起的振动以及外部绕流引起的涡激振动(Vortex Induced Vibration, VIV),从而容易导致其疲劳失效。人们长期以来更多地关注立管外部流体产生的涡激振动问题,缺乏对内输流体特别是多相流和涡激耦合作用下的深入研究。海洋管线内部一般都是输送高温、高压的油气水混合体,其成分组成及运动特性非常复杂。本文拟对内输多相流的立管的涡激振动进行研究。
当海流流经立管,在立管两侧形成涡漩脱落,从而在立管上产生波动的横向力和流向力,使立管产生位移,即VIV。黄维平等[1]提出一个非线性的圆柱体涡激振动时域分析模型,同时考虑了顺流向和横向的流固耦合问题。张永波等[2]通过涡激振动模型实验的方法,研究了顶张力立管在海流作用下的涡激振动规律。海洋管线除了要承受因为外流涡激释放产生的振动外,还需要承受管线内流的作用。内流对输流管线的振动分析主要集中在不同管内流体流速对于管线的振动幅值、频率、振型的影响,以及发生管线失稳状态下的内流临界速度。Kaewunruen等[3]通过耦合轴向和横向振动来建立海洋输油立管的非线性模型,并对柔性刚度、顶部张紧力及内流速度进行了定量分析。孟丹等[4]考虑内流和外流的联合作用,建立输流管道的二维非线性涡激振动方程,分析了不同内外流流速以及内外流联合作用对管道稳定性的影响。Gu等[5]研究了输流管线的响应与内流速的关系,并进一步得出管线振动幅值与内部流体流速的关系。Guo等[6]通过实验方法研究了小尺寸管线模型在内流和涡激耦合作用下的动力响应,除了验证了内流速的增加会降低管线自然频率外,还指出随着内流速的增加,来流向和横流向的振动幅值都会增加。随管内流速的增加,管道会发生失稳现象,内输流体存在临界内流速。Dai等[7]研究了两端铰链的内输流体管的涡激振动,采用四阶迦辽金方法分析了管内流速从次临界区变化到超临界区对管道涡激振动的影响以及不同内流速下和外流速下管道的振动锁定、周期振动和振动分岔现象。Meng等[8]采用迦辽金方法和差分法也分析了管内流体流速从次临界区增加到超临界区对管道涡激振动的影响,分析出当管内流速超过临界值时,管道会出现屈曲颤振耦合的不稳定。Dai等[9]研究内输脉动流体的海洋管道的涡激振动,通过在稳定的内流速上加一周期性变化的量模拟管内的脉动流体,分析了内输脉动流体的管道参数共振和涡激振动锁定现象并与内输稳定流进行了对比。
海洋管线中一般为油、气、水混合的多相流动,多相介质的存在,多相流的流动不稳定改变了管线系统的动力学特性。各相之间密度、流速、所占体积比的不同会引起内部流体的质量、动量、压力等波动,从而导致管线的振动和作用力的波动。Monette等[10]通过实验和数值计算,分析了管内流体速度和气液比对管线振动响应的影响,提出一个修正的两相流模型。An等[11]计算了内输气泡流管线的振动响应,分析得到系统的自然频率随体积含气率的增加而减小。目前对于海洋管线运输多相流的研究甚少,内部两相流作用与外部流体涡激振动耦合作用下的管线振动的研究几乎空白。
本文主要研究张紧式立管,考虑内输多相流与涡激振动耦合作用,建立内部两相流-立管-外流的耦合方程,通过广义积分变换法对耦合的模型进行精确求解,针对管内两相流作用对内输流体立管的自然频率以及内外流共同作用下立管发生涡激振动的频率和幅值参数的影响进行研究。
1 物理模型
由于张紧式立管在水下是基本垂直的,可以将立管看成是薄壁细长梁,TTR立管可以采用欧拉梁模型进行模拟。将海洋环境中运输油气的立管简化为一个两端简支的内输两相流管线。其置于横向流动的流体中,如图1所示。外部流体在立管附近发生涡街释放,从而引起立管振动。
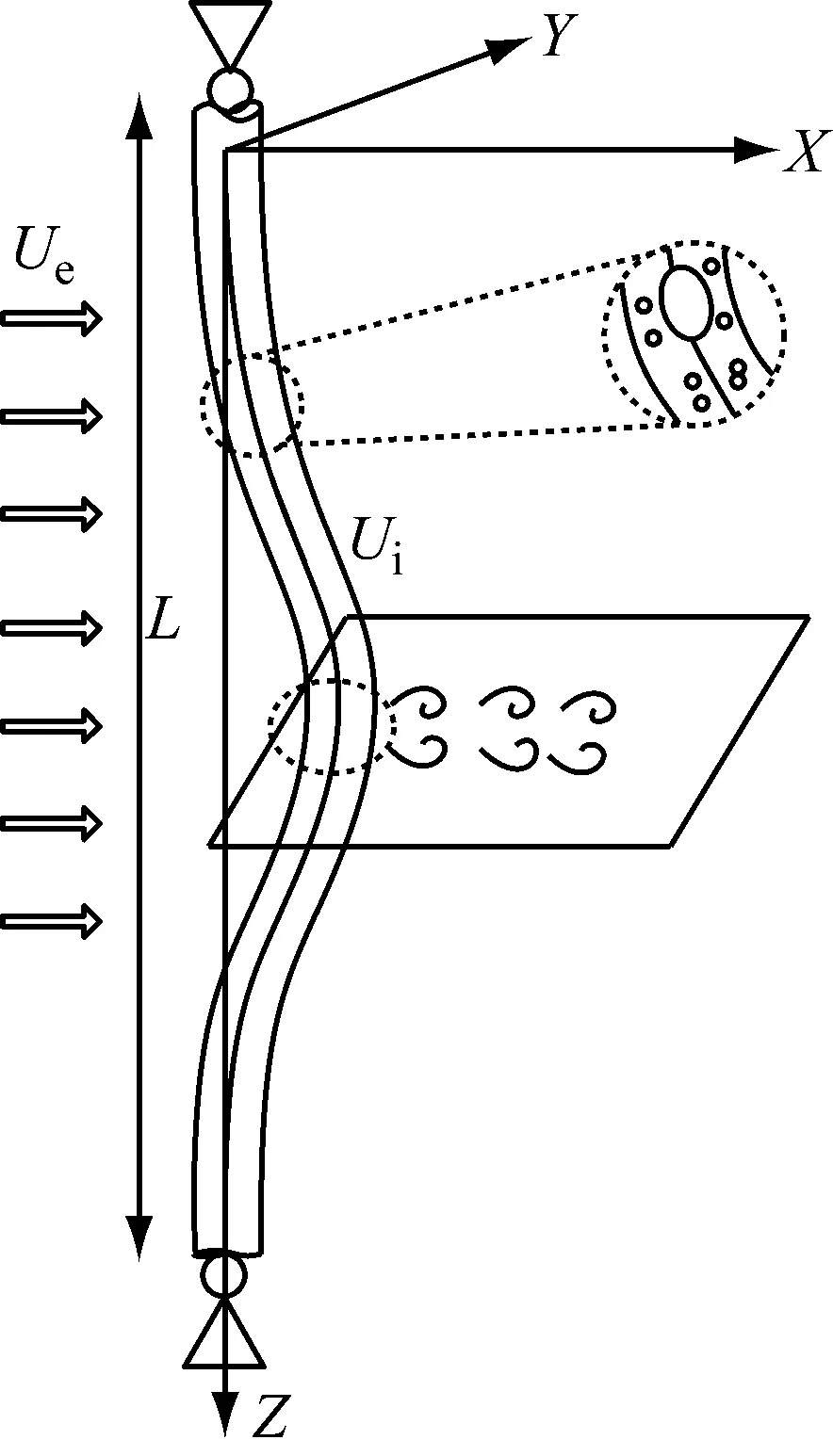
图1 内输多相流立管与外部绕流示意图
1.1 内部气液两相流-立管-外流耦合方程
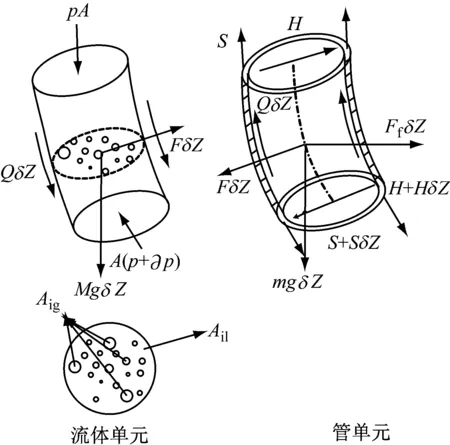
图2 管内气体、液体单元和管单元受力分析
由于立管的长细比足够大,可近似采用欧拉梁模型模拟,忽略立管的横向剪切变形。分别对管单元、气体单元和液体单元进行受力分析,如图2所示。在分相流动基本方程推导过程中,一般将两相分别按单相流处理并计入相间的相互作用,两相间发生质量、能量和动量传递,后按需要将各相的方程加以合并。液体、气体和管单元在管线轴向和横流向的受力平衡方程为,
GgdUig+UigdGg-UildGg
(1)
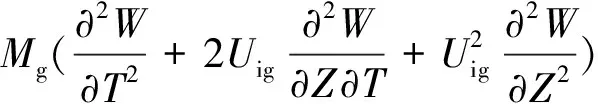
(2)
-Ail∂p+Ql∂Z-τ∂Z+Mlg∂Z-

(3)
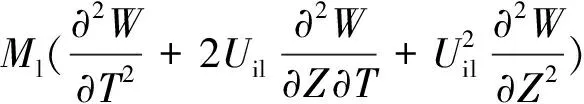
(4)
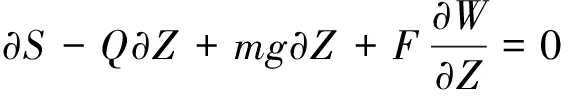
(5)
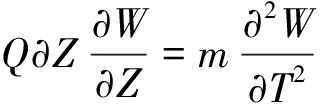
(6)
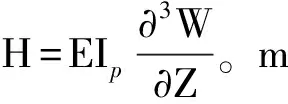
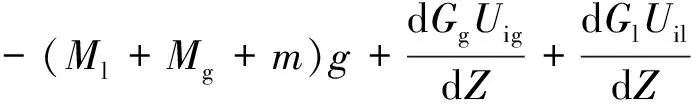
(7)
将其从Z到L进行积分,得到立管在Z处满足
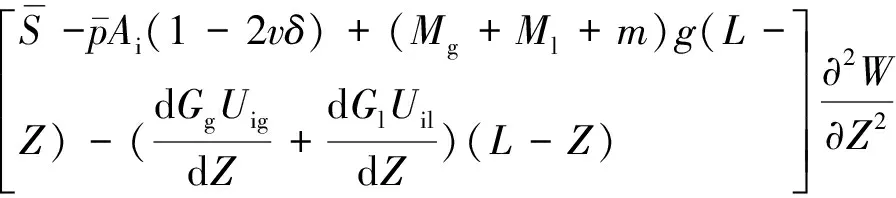
(8)
将式(2)、式(4)和式(6)相加,得到内部两相流-立管-外流耦合的方程。即横流向,Y方向,满足的方程
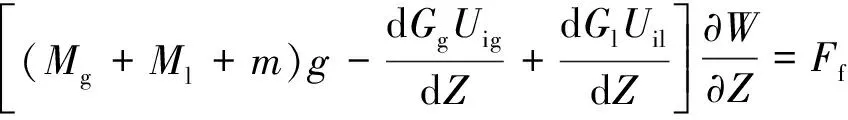
(9)
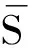
(10)
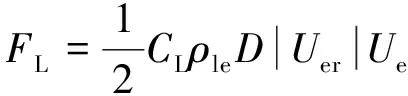
(11)
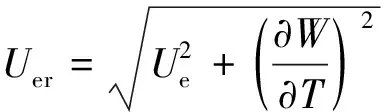
(12)
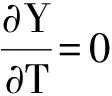
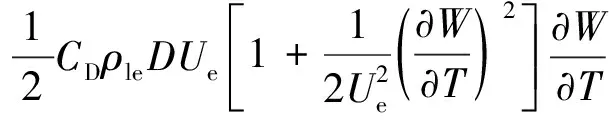
(13)
采用非线性尾流振子的半经验模型模拟外流与管线的涡激振动,将流体和管线看作整体系统,尾流为一个非线性振子且满足非线性Van der Pol方程[12]。则升力系数CL表示为
CL=CL0q(Z,T)/2
(14)
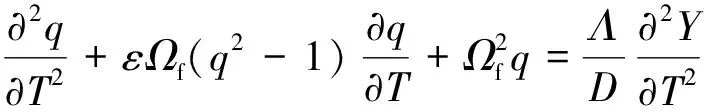
(15)
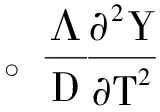
对于简支-简支的立管,其边界条件表示为
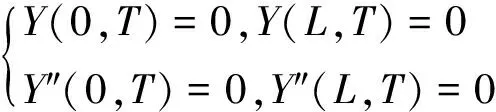
(16)
给振荡力设置一个初始的随机作用,其幅值为O(10-3)。立管位移和速度的初始条件都设为0,
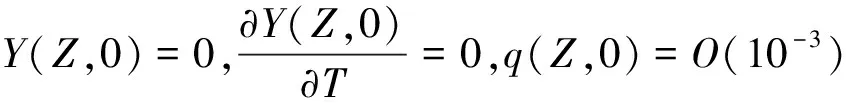
(17)
1.2 两相流模型
多相流流型多变,主要包括,气泡流、段塞流、环状流、涡流、分层流,不同的流型对管线的作用方式、作用力和振动的影响差异很大。两相流重要的表征参数有容积含气率εg,截面含气率αg以及两相流之间存在的不同程度滑动的滑速比K
(18)
式中:Qg和Ql为气相和液相的容积流量;Ag和Al分别为气相和液相所占的截面面积;Uig和Uil分别为管内气相和液相真实速度。以上三个参数满足
(19)
则管内各相质量和流速为
Mg=ρgAg=ρgαgAi
Ml=ρlAl=ρl(1-αg)Ai
(20)
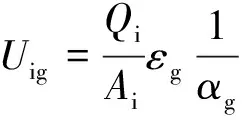
(21)
Monette等在观察了不同的两相流流型的基础上,通过实验和数值计算,提出一个修正的两相流模型。其在观察了不同的两相流流型的基础上,通过一系列内输两相流管道的振动实验,分析内输多相流管道的振动特性,得到实验结果和采用修正的两相流模型的理论结果十分吻合。修正的两相流模型中滑速比是截面含气率的函数,
(22)
采用下面的无量纲化参数,对横向运动方程以及尾流振子方程进行无量纲化。
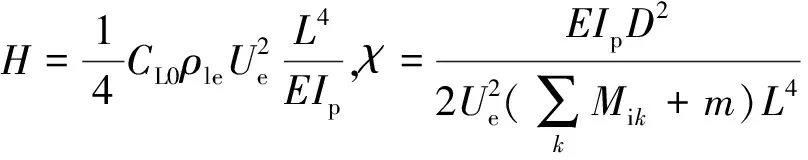
(23)
k代表管内不同相的流体,即本文的液相和气相。结合式(9)、式(13)、式(14)、式(15)和式(23),得到立管在内流和外部绕流耦合作用下的无量纲形式运动方程组
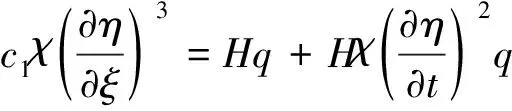
(24)
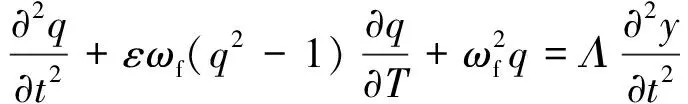
(25)
边界和初始条件为
η(0,t)=0,η(1,t)=0,η″(0,t)=0,η″(1,t)=0
(26)
2 数值求解
尾流振子模型是一组耦合的偏微分方程组,其数值解法有很多选择,最常用的是有限差分法(Finite Difference Method, FDM)[13-14],以及有限元法(Finite Element Method, FEM)[15-16]。广义积分变换法(Generalized Integral Transform Technique, GITT)是一种半数值-半解析的方法,其最大的优点就是能够自动前向控制全局误差,因此该方法特别适用于各种计算的基准测试。 GITT法在传热问题[17]和三维纳维斯托克斯方程的求解[18]中得到了广泛应用,而在固体结构计算中的应用才刚刚开始。本文采用GITT方法将偏微分方程组转化为一系列可以求解的常微分方程组。根据广义积分变换的原理,选用满足边界条件的特征值方程,并对待求方程进行特征函数展开。立管横向位移η满足边界条件式(26),则选用横向位移的特征值方程φ满足
(27)
以及边界条件
φi(0)=0,φi(1)=0,
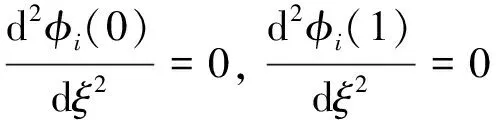
(28)
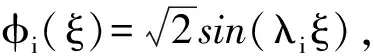
(29)
升力系数q(ξ,t)的特征值问题满足
(30)
式中:μm为特征值,φm(ξ)为特征值方程,同样满足正交性条件。升力系数的特征方程和特征值与横向位移相同。升力系数的积分变换对为
(31)
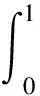
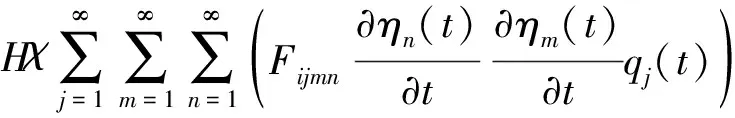
(32)
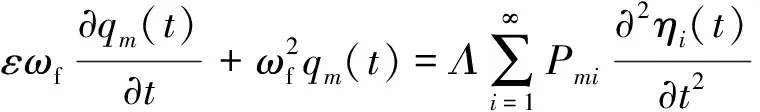
(33)
式中:
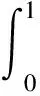
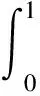
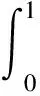
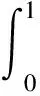
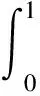
(34)
同样的,对初始条件进行广义积分变换,得到
(35)
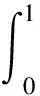
(36)
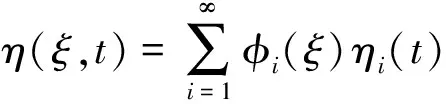
3 结果分析
本文采用的立管参数和流体参数,如表1所示。
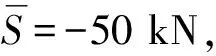
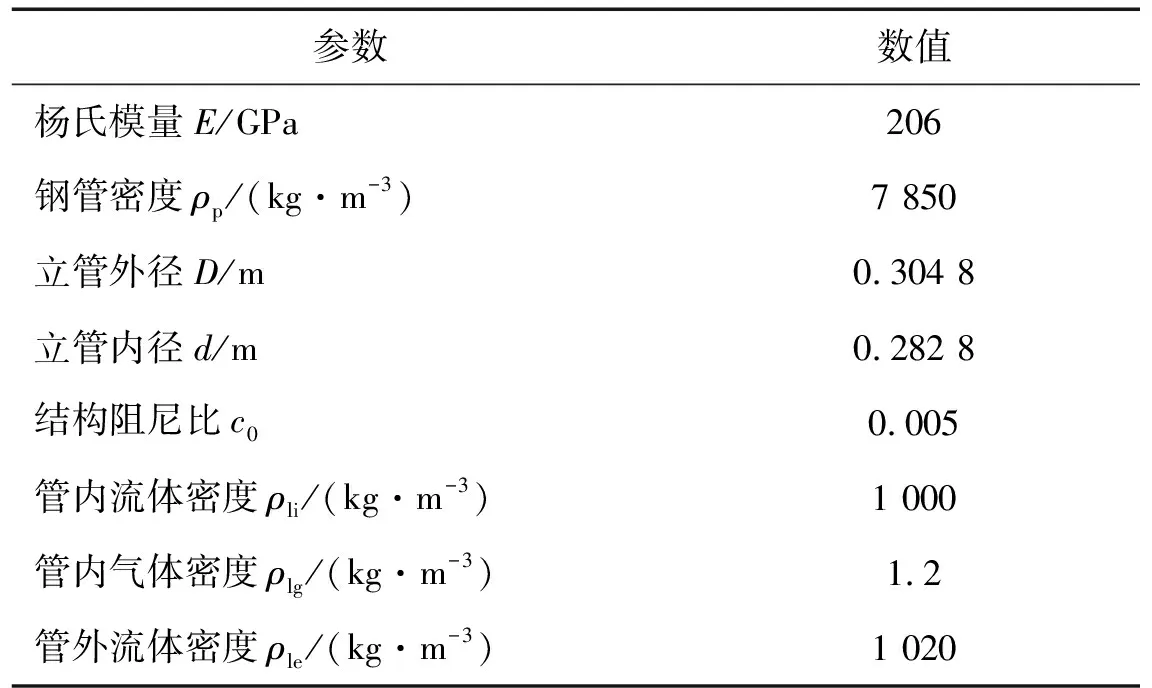
表1 立管和流体参数
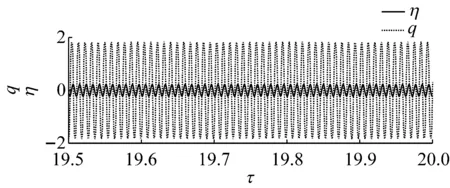
(a) 立管振动时程曲线

(b) 振动频谱分析
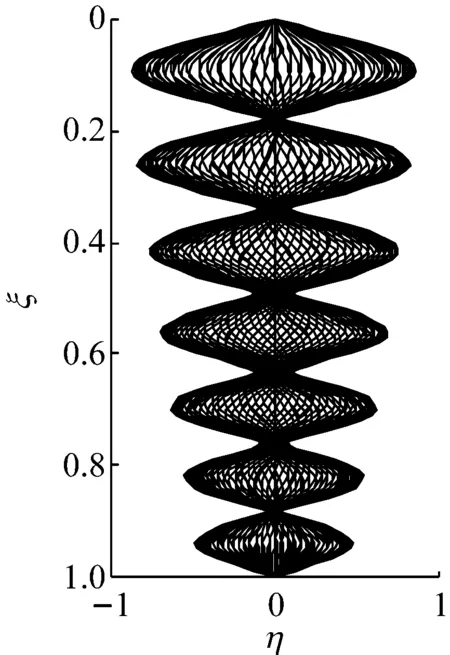
图4 立管上各点不同时刻下的横向位移
3.1 管内两相流对立管自然频率的影响
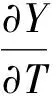
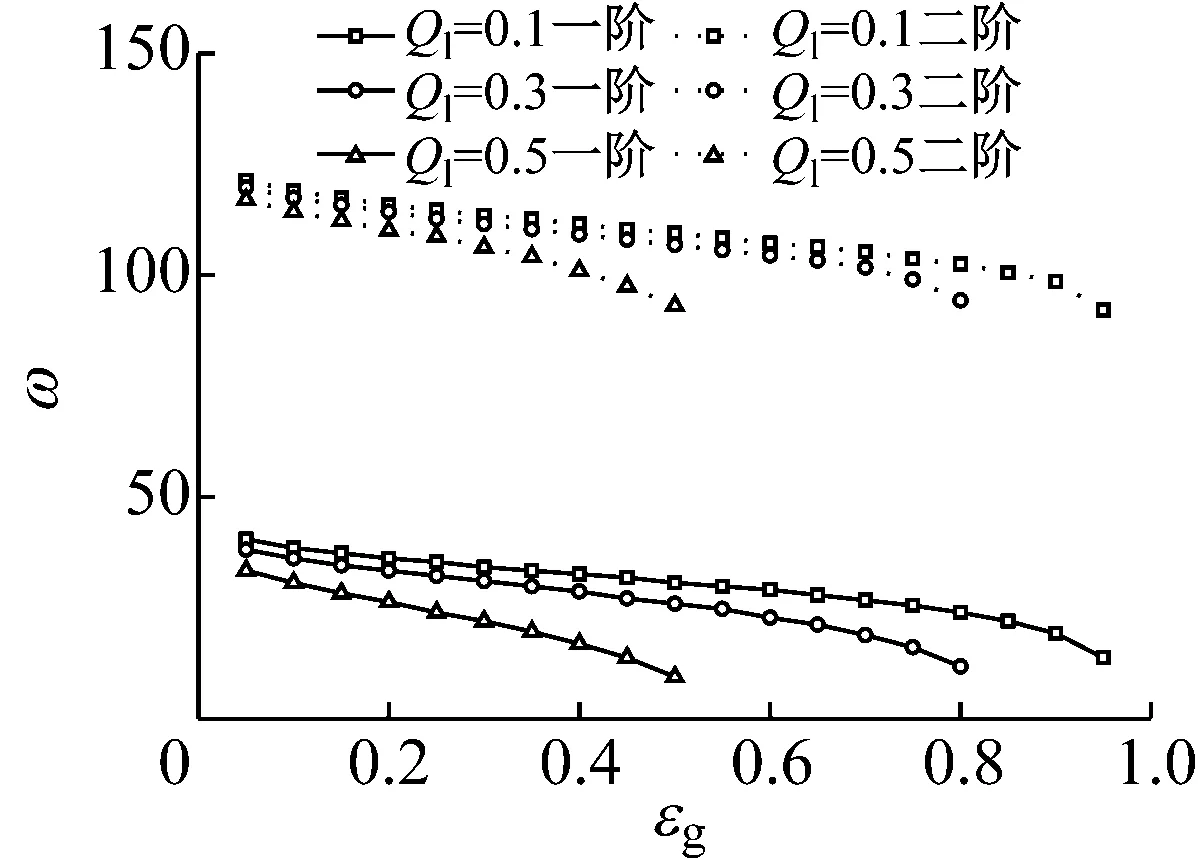
图5 管内输不同流速立管的自然频率与气液体积比的关系
同时分析了不同立管长度下,立管各阶自然频率随管内容积含气量的变化。在前人的分析中,忽略管道及管内流体所产生的重力压降和对管道轴力的影响,因而管道的无量纲自然频率与管道长度无关。Gu等分析得到采用欧拉梁模型的管道随长细比的增加,其无量纲自然频率为一定值。本文由于考虑了重力压降以及管道轴力的变化,则由管道轴力和内部压强产生的作用满足式(8),其受管道长度的影响,则不同管道长度下,管道的无量纲自然频率有变化。因此对不同长度立管下,管道内两相流对管道振动特性的影响进行了分析。图6为内流速Ql=0.2 m3/s,立管长细比分别为500,1 000,2 000时,立管的自然频率随容积含气率的变化图,其对应的值见表3。从图6同样可知,随立管内气体的增加,立管的各阶自然频率降低,并且立管越长,各阶自然频率随含气量增加而降低得越明显,临界容积含气率越小。如当容积含气率εg从0增加到0.5时,长细比为500的立管的一阶无量纲频率从17.28降低到14.14,而长细比为2 000的立管的一阶无量纲频率从97.38降低到56.15。从而得出结论,立管越长,管内两相流作用越明显。图7为不同立管长细比和不同管内流量的情况下,立管内输两相流的临界体积含气率。从图7可知,立管越长,内部流体流量越大,立管的临界含气率越小。
表2不同内流速和气液体积比下的立管自然频率
Tab.2Naturalfrequenciesofriserwithdifferentflowratesandvolumetricgasfractions
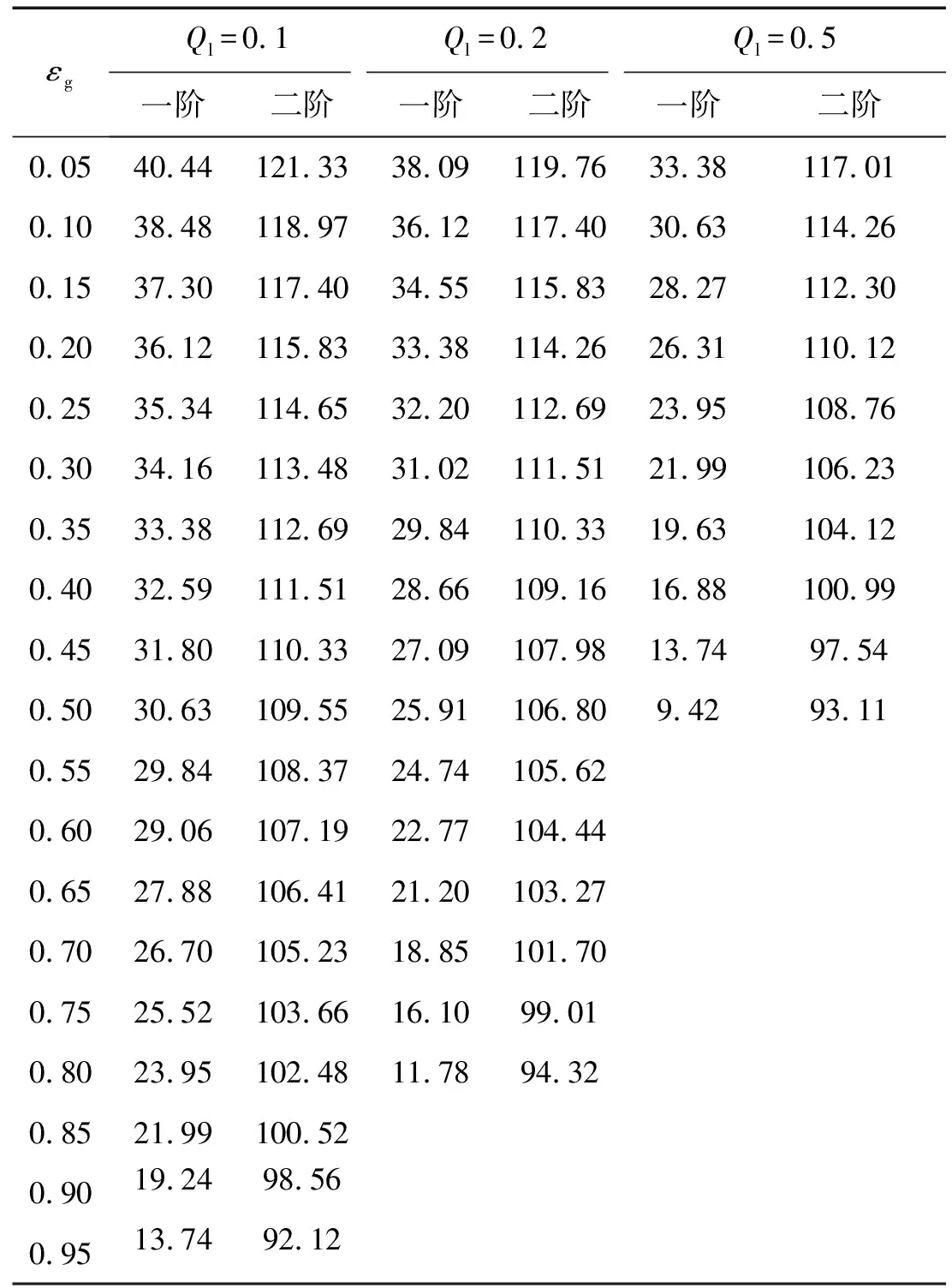
εgQl=0.1Ql=0.2Ql=0.5一阶二阶一阶二阶一阶二阶0.05 40.44 121.33 38.09 119.76 33.38 117.01 0.10 38.48 118.97 36.12 117.40 30.63 114.26 0.15 37.30 117.40 34.55 115.83 28.27 112.30 0.20 36.12 115.83 33.38 114.26 26.31 110.12 0.25 35.34 114.65 32.20 112.69 23.95 108.76 0.30 34.16 113.48 31.02 111.51 21.99 106.23 0.35 33.38 112.69 29.84 110.33 19.63 104.12 0.40 32.59 111.51 28.66 109.16 16.88 100.99 0.45 31.80 110.33 27.09 107.98 13.74 97.54 0.50 30.63 109.55 25.91 106.80 9.42 93.11 0.55 29.84 108.37 24.74 105.62 0.60 29.06 107.19 22.77 104.44 0.65 27.88 106.41 21.20 103.27 0.70 26.70 105.23 18.85 101.70 0.7525.52103.6616.1099.01 0.80 23.95 102.48 11.78 94.32 0.85 21.99 100.52 0.90 19.24 98.56 0.95 13.74 92.12
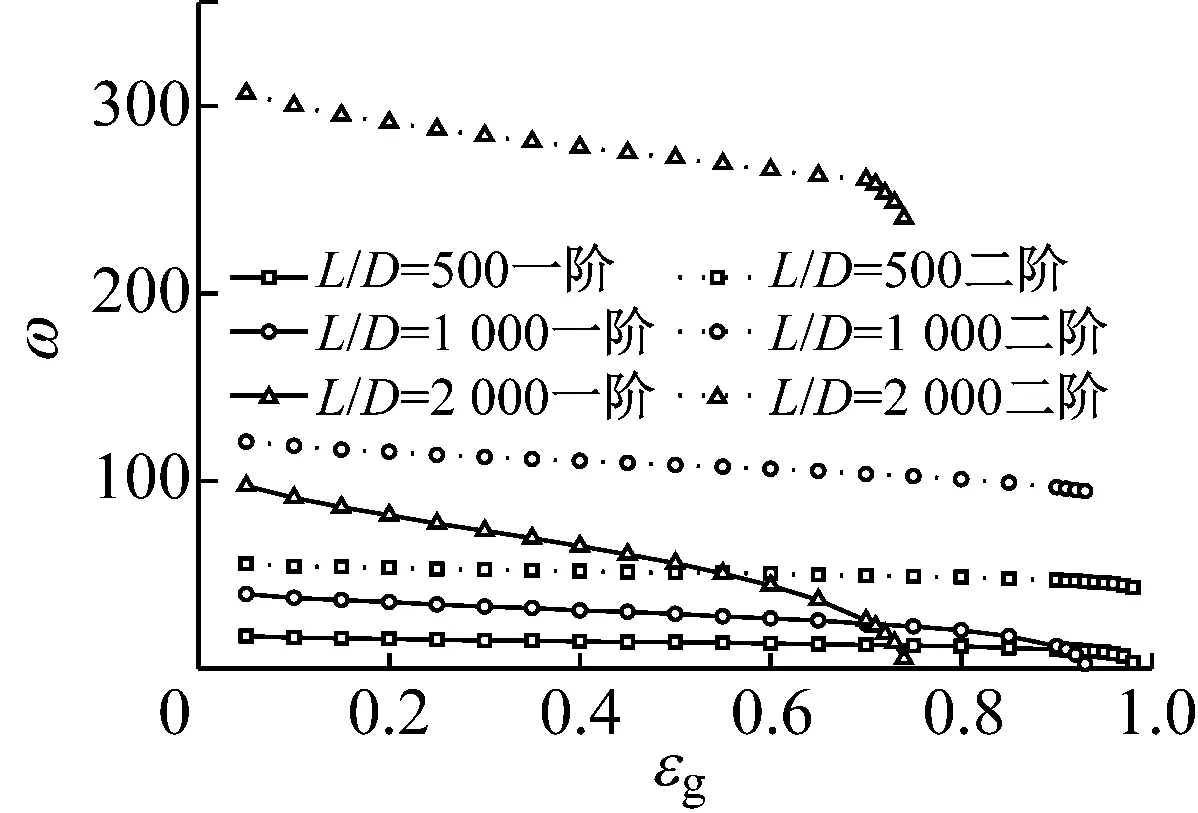
图6 不同长度下立管自然频率与气液体积比的关系
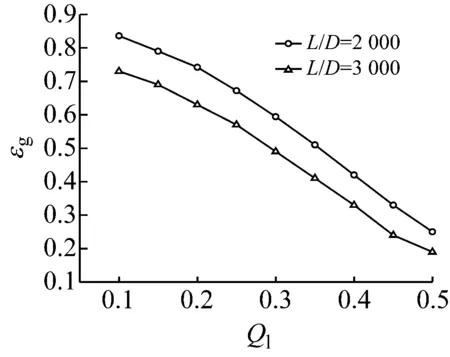
图7 不同长细比和内流流量下内输两相流立管的临界容积含气率
Fig.7 Critical volumetric gas fraction of riser conveying two-phase flow with different aspect ratios and volumetric flow rates
表3不同长细比和气液体积比下的立管自然频率
Tab.3Naturalfrequenciesofriserwithdifferentaspectratioandvolumetricgasfractions
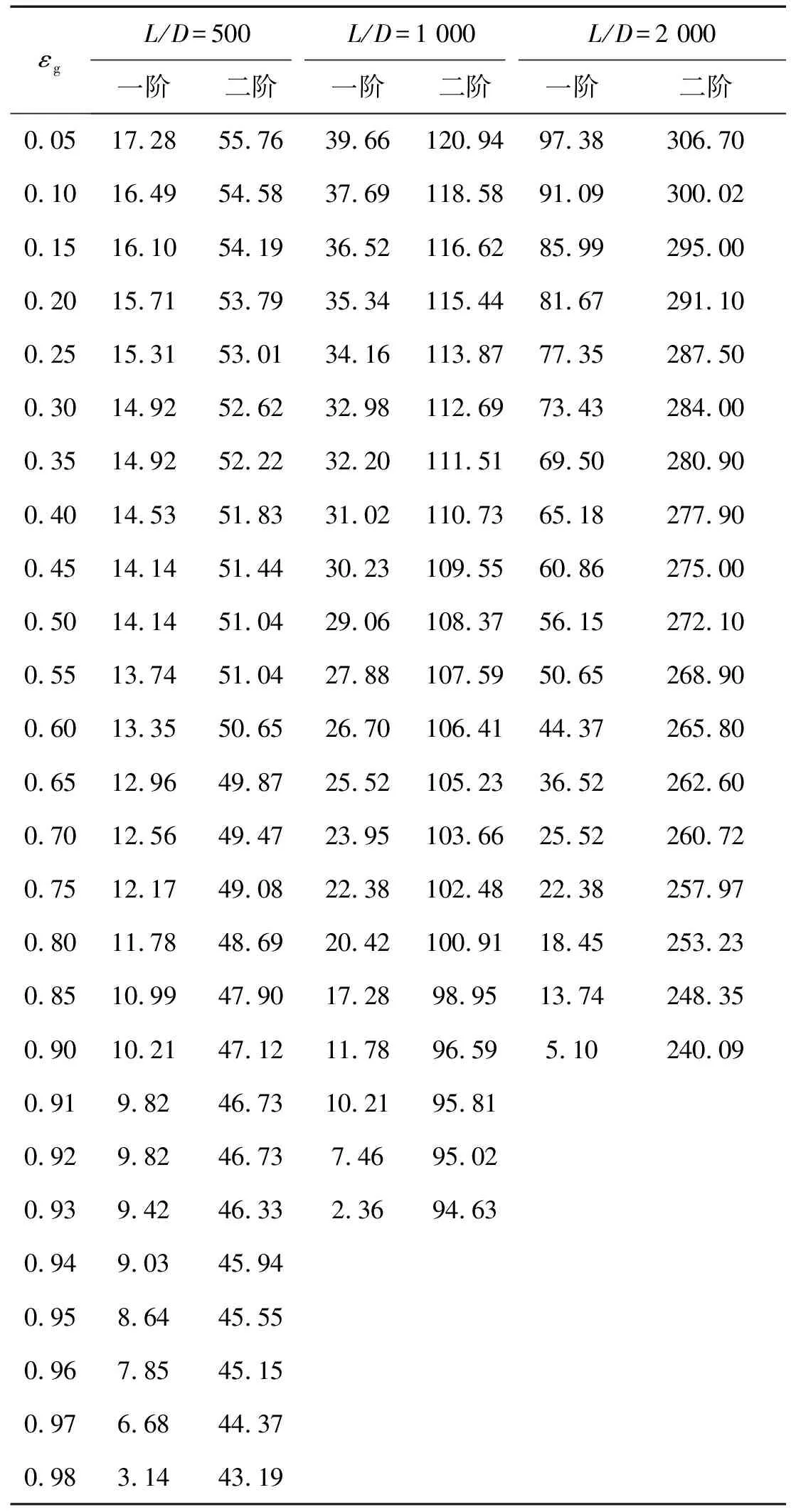
εgL/D=500L/D=1 000L/D=2 000一阶二阶一阶二阶一阶二阶0.0517.2855.7639.66120.9497.38306.700.1016.4954.5837.69118.5891.09300.020.1516.1054.1936.52116.6285.99295.000.2015.7153.7935.34115.4481.67291.100.2515.3153.0134.16113.8777.35287.500.3014.9252.6232.98112.6973.43284.000.3514.9252.2232.20111.5169.50280.900.4014.5351.8331.02110.7365.18277.900.4514.1451.4430.23109.5560.86275.000.5014.1451.0429.06108.3756.15272.100.5513.7451.0427.88107.5950.65268.900.6013.3550.6526.70106.4144.37265.800.6512.9649.8725.52105.2336.52262.600.7012.5649.4723.95103.6625.52260.720.7512.1749.0822.38102.4822.38257.970.8011.7848.6920.42100.9118.45253.230.8510.9947.9017.2898.9513.74248.350.9010.2147.1211.7896.595.10240.090.919.8246.7310.2195.810.929.8246.737.4695.020.939.4246.332.3694.630.949.0345.940.958.6445.550.967.8545.150.976.6844.370.983.1443.19
3.2 内流与外流耦合作用下立管振动特性分析
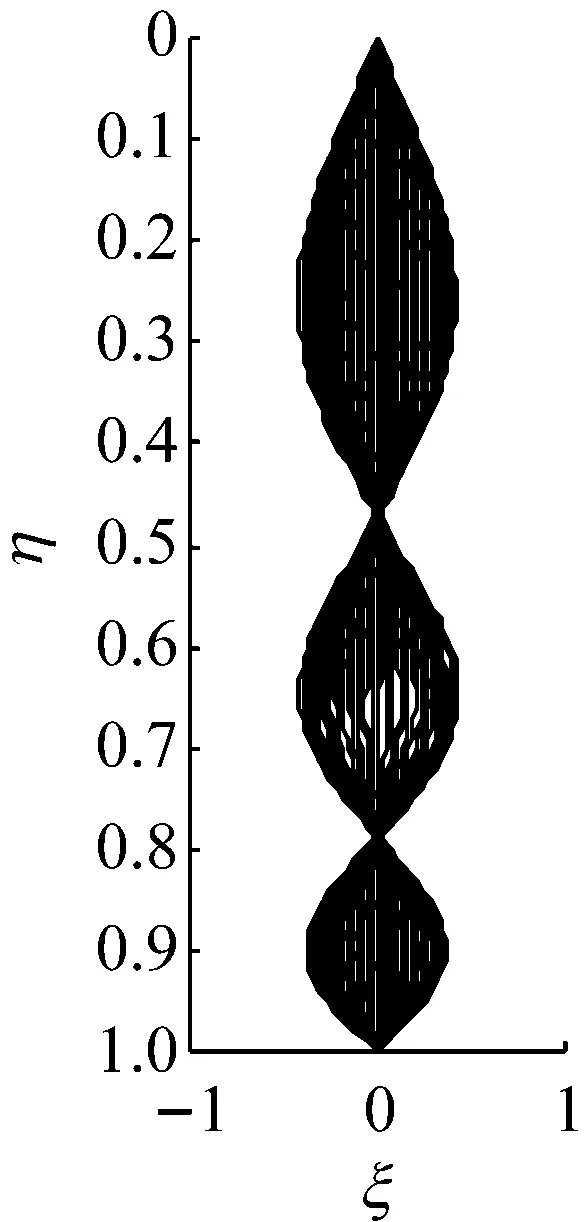
前面分析了管内两相流对立管振动固有属性,即立管自然频率的影响,得到两相流的作用会使立管自然频率降低。在此基础上分析内外流耦合作用下,两相流对立管涡激振动的影响。当立管长细比为1 000,管内液体流速Ql为0.2 m3/s,气液体积比分别为εg=0、0.5、0.9,外部绕流流速从0.1 m/s增加到0.5 m/s时,立管的振动频率,如图8所示。从图8可知,立管振动的频率随外流速的增加逐渐增加,并且随外流速的进一步增加,振动频率发生急剧增加,从低一阶模态的振动跳跃到高一阶模态振动。立管内气体含量越高,相同外流速下立管振动频率较小。由前面的分析可知,立管的自然频率随管内气液比的增加而降低。虽然外部涡街释放频率为一个定值,但立管内两相流体引起立管自然频率的降低,会引起立管发生共振的外部流体的流速减小。并且,管内的两相流引起的立管自然频率的降低会使立管在一定的外部绕流速下发生更高一阶模态的振动。内部两相流的增加会使立管从低阶模态振动跳跃到高阶模态振动的点发生左移,如图8所示。如当外流速为0.22 m/s时,管内不含气体的立管以二阶模态振动,容积含气率为0.5和0.9的立管发生三阶模态振动,如图9所示。随外流速的增加,不同管内含气量立管发生模态跳跃的点逐渐趋于一致。从图中看出,容积含气量为0,0.5和0.9的立管都在外流速为0.47 m/s时,从四阶模态振动转为五阶模态振动。
图10为气液体积比分别为εg=0、0.5、0.9,内输多相流立管的振幅随外部流体流速的关系,其中立管长细比为1 000,管内液体流速Ql为0.2 m3/s。从图10可知,立管的振动幅值出现4个峰值,分别对应于立管一阶、二阶、三阶和四阶模态发生的共振。当外部涡街释放频率逐渐接近于立管自然频率时,立管振幅有显著增加。随外部流速的进一步增加,立管振动从低阶模态向高阶模态发生跳跃时,立管振动幅值急剧降低。并且管内含气量越高,立管发生模态变化的点左移,如当含气量为0时,立管的振幅在外流速为0.11 m/s时发生振幅的急剧降低,立管振动从一阶模态振动变化为二阶模态振动;而含气量为0.5的立管在外流速为0.10 m/s时,振幅发生急剧降低。则一定外流速下,管内的高含气量会引起立管发生更高一阶模态振动,如外流速为0.11 m/s时,管内输单相流体时的立管发生一阶模态振动,而含气量为0.5的立管发生二阶模态振动。管内含气量越高,相同外流速下立管振幅越大。同时,立管内两相流会使立管发生共振的点向左发生偏移,且共振时的振幅较大。这主要是因为管内两相流作用使立管的自然频率降低,从而引起立管发生共振的外流速降低。较低的外流速下,管外绕流对立管的阻力降低,从而立管发生共振的幅值增加。当管外绕流引起立管发生高阶模态振动,即外流速增加时,不同含气量的内输流体立管的振动幅值逐渐接近,管内两相流作用逐渐减小。如当外流速为0.03 m/s时,不含气体的内输流体立管的振动幅值为0.016,而含气量为0.5的内输流体立管的振动幅值为0.420。而外流流速为0.45 m/s时,内部不含气体的立管振动幅值为0.800,而含气量为0.5的立管的振动幅值为0.801.因而可以得出结论,管内两相流作用会使立管振动幅值增加,发生共振的外流速降低。立管内的含气量的增加会引起立管发生更高一阶模态的振动。以及外流速越高,立管内的两相流作用越小,不同含气量管线的振动幅值趋于一致。
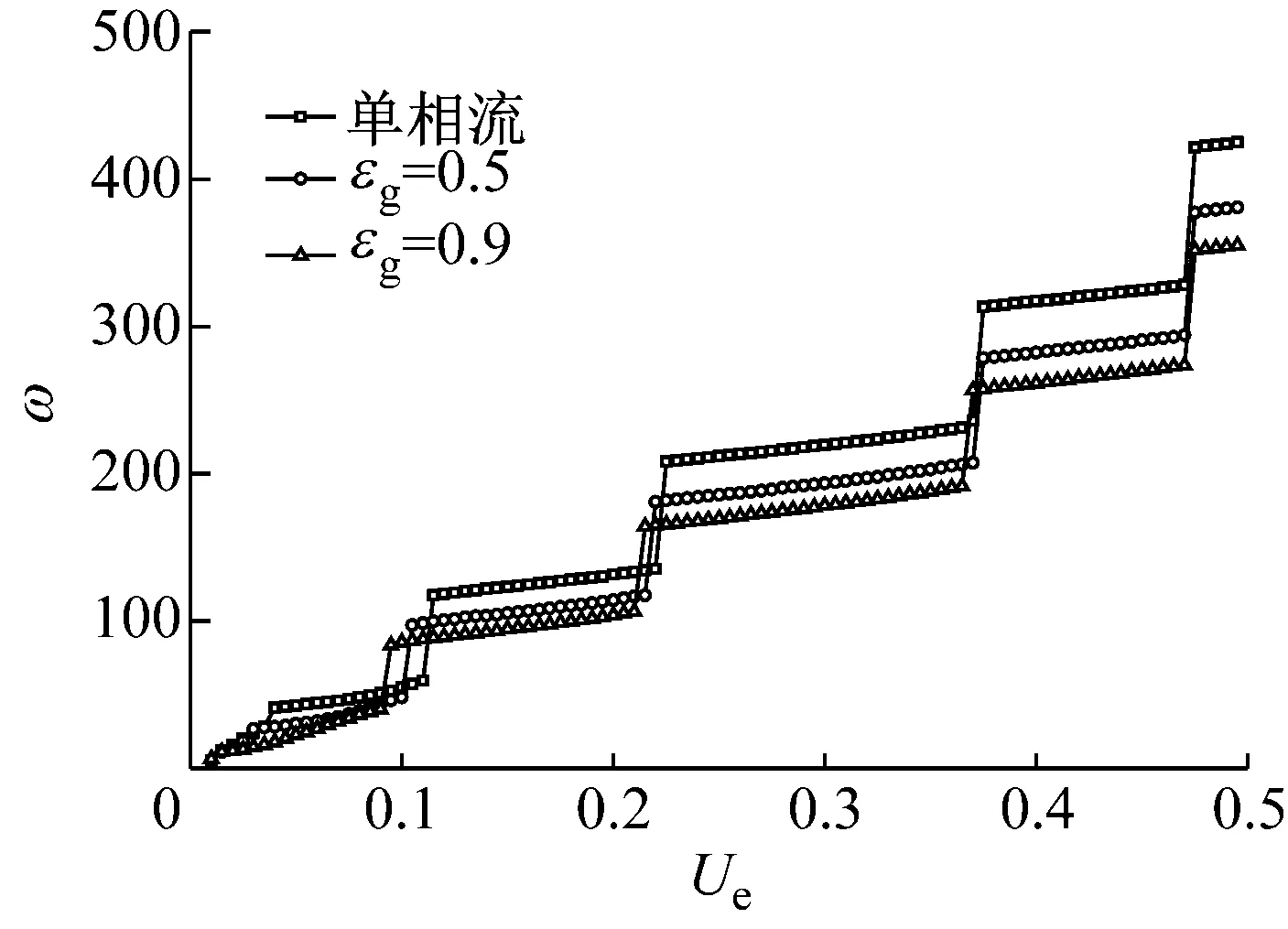
图8 不同外流流速下内输多相流立管的振动频率
Fig.8 Dimensionless frequencies of riser conveying multi-phase flow versus external flow velocity
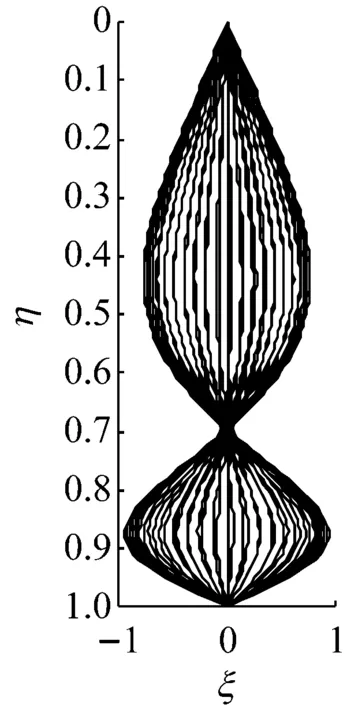
内输单相流
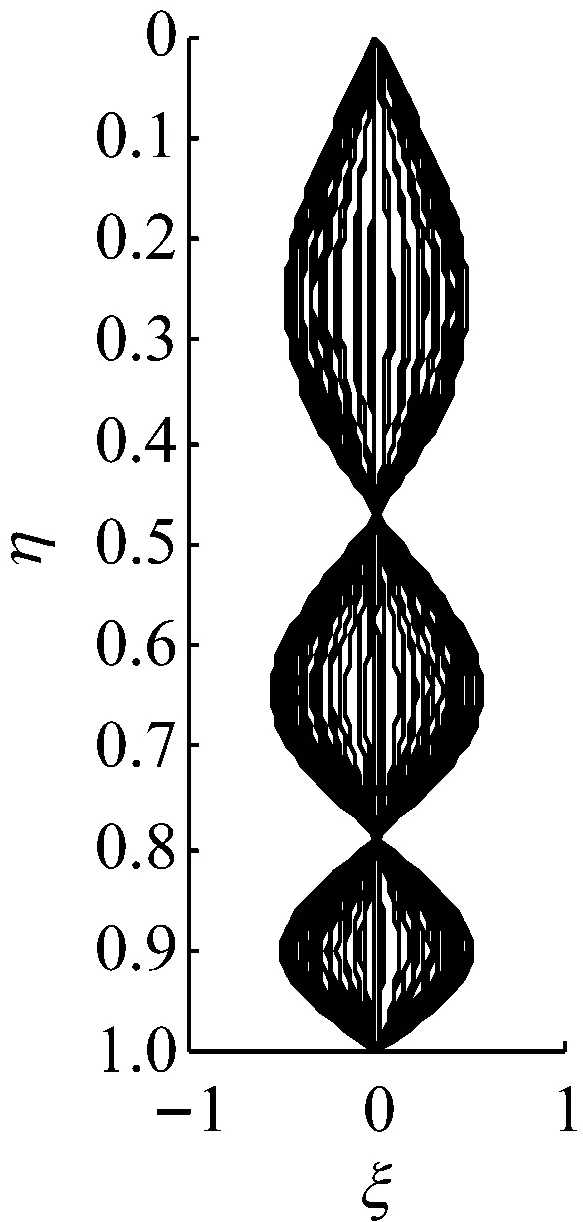
含气率为0.5
含气率为0.9
图9 不同含气率下立管的振动形态
Fig.9 The vibration shape of riser with different volumetric gas fraction
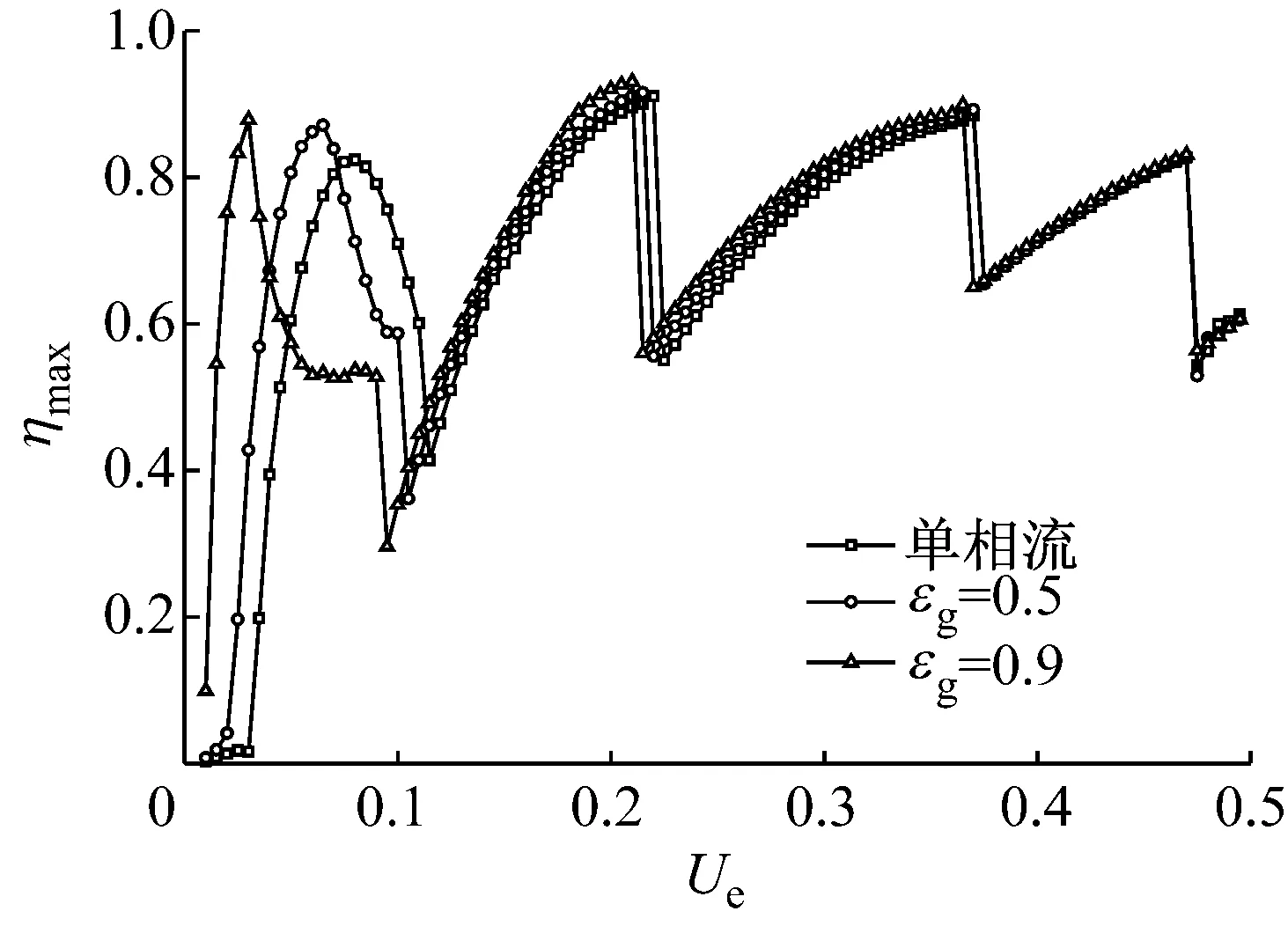
图10 不同外流速下内输多相流立管的无量纲振动幅值
Fig.10 Dimensionless amplitudes of pipe conveying multi-phase flow versus external flow velocity
4 结 论
结果表明,在实际海洋环境和操作环境中,需要考虑内输多相流体对立管振动的影响。内部两相流会导致立管自然频率的降低。内输气液两相流立管存在临界的含气量。立管越长,管内流速越高,管内两相流作用越明显,临界体积含气量越低。内流和外流共同作用下,两相流会使立管振动频率降低,振动幅值增加。随管内含气量的增加,立管发生共振对应的外流速降低,立管共振时对应的振动幅值也越大。并且相同外流速下,管内两相流会诱发立管的更高一阶模态振动。外流速越高,立管内的两相流作用越小,不同含气量立管振动幅值越接近,立管发生模态变化时对应的外流速也近乎相同。
