高铁桩网复合路基环境振动影响因素分析
2018-12-21高广运戴益波杨成斌
高广运, 戴益波, 雷 丹, 杨成斌
(1.同济大学 岩土及地下工程教育部重点实验室,上海 200092;2.上海岩土工程勘察设计研究院(集团)有限公司,上海 200032;3.合肥工业大学 资源与环境工程学院,合肥 230009)
近年来,我国高铁迅速发展,而沿海大部分地区以及内陆部分地区存在着大面积的深厚软弱土层,为了提高行车舒适度和控制路基沉降,桩土复合路基被广泛采用[1],其中,桩网结构是复合地基的一种重要形式。列车运行引起的复合路基地面环境振动与传播问题越来越受到人们的关注。
目前高铁运行引起的环境振动的研究,多把复合路基视为天然路基,仅少数论文对复合地基进行分析。李华明等[2]以京沪高速铁路液化土地基加固为背景,利用大型堆叠式剪切变形模型箱,进行了CFG 桩桩网结构地基加固饱和粉土地基的振动台模型试验,分析了CFG加固饱和粉土地基的动力特性。马利衡等[3]建立数值模型研究了沪宁城际高速铁路列车运行引起的环境振动特性和振动传播规律,分析了桩网结构地基加固方式和土质条件对振动的影响。Thach等[4]建立了列车荷载作用下桩体加固路基动力分析三维模型,发现随车速增加列车荷载模式与轨道位移模式差异越大,路堤和地基加固体对高频振动有较强吸收作用,减小了远离路堤的地面振动。Kouroussis等[5]采用分步三维模型研究了不同土体参数及均质和分层土路基在脉冲荷载和列车荷载作用下的地面振动规律,发现土体分层对地面振动有较大影响。高广运等[6]采用等代模量法将CFG桩简化为桩墙,并结合上部列车-轨道模型与下部路基模型,建立了列车-轨道-路基整体2.5维有限元分析模型,研究了CFG复合路基对地面振动的影响。等代模量法虽然在一定程度上能考虑复合桩基的影响,但概念仍较模糊。
已有成果多对桩网复合地基进行了简化,或仅对具体工程桩网复合路基环境振动问题进行了研究,未对影响地基环境振动的多种因素进行分析,更符合实际的桩土复合路基模型有待建立。鉴此,本文基于ABAQUS软件,建立高速铁路列车荷载下包含垫层、桩帽、桩体的轨道-路堤-桩网复合路基三维动力有限元模型,分析了车速、路堤高度及土体阻尼比对高铁复合路基地面环境振动的影响。
1 列车荷载模拟
模拟列车荷载的方法有多种[7],本文采用人工激励力模拟,通过对路基的振动频域特性进行分析,人为将列车荷载模拟成一系列周期荷载的叠加,然后通过不同车型、车速等因素来调整相应参数,从而得到具体的列车荷载时程曲线。采用文献[8]中的人工激励力表达式
(1)
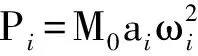
模型的列车动荷载根据京沪高铁和谐号CRH 380AL型电力动车组参数确定,设计轴重不大于150 kN,因此取单边轮重75 kN,列车单边轮簧下质量M0=1 000 kg。取相对应的典型不平顺振动波长和矢高分别为:L1=10 m,a1=3.5 mm;L2=2 m,a2=0.4 mm;L3=0.5 m,a3=0.08 mm;k1=1.538,k2=0.7。
本文分析考虑了荷载移动效应,通过ABAQUS荷载子程序DLOAD的方式进行施加。
2 模型可靠性验证
Zhai等[9]对京沪高铁近苏州东站处路基段地面振动进行了实测分析。为了验证模型的合理性,依据相应的工况,采用ABAQUS软件建立相应的三维有限元模型,并将模拟结果与实测结果进行对比分析。
2.1 模型建立
轨道模型采用京沪高速铁路的CRTSII型板式无砟轨道结构形式,主要参数,如表1所示[10]。钢轨采用梁单元进行模拟,轨道板、CA砂浆层和混凝土底座采用三维实体单元进行模拟;扣件间距0.65 m,橡胶垫板刚度为2.50×107N/m,阻尼为7.50×104N·s/m,为了简化考虑,模型中采用弹簧阻尼器来等效模拟扣件系统。
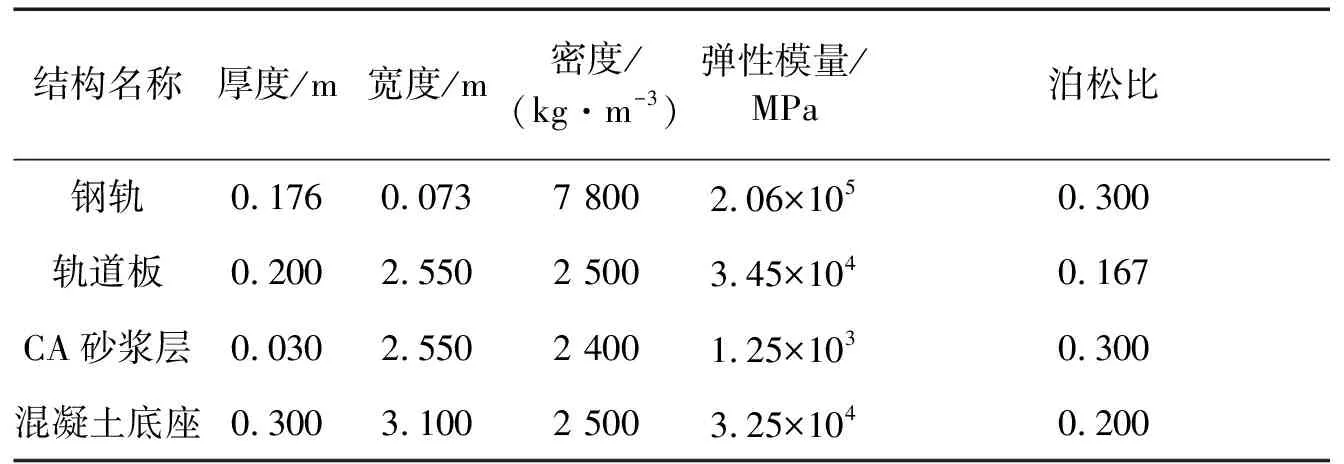
表1 我国CRTSⅡ型板式无砟轨道结构参数
考虑到研究问题的对称性,仅取轨道和路基的一半进行建模。Yang等[11]通过大量研究表明,三维有限元模型选用4节列车同时运行,基本可满足数值研究的精度需要。根据CRH380AL型动车组的具体尺寸,4节(2T2M)车厢的总长度为103 m,为保证精度,本文有限元模型沿轨道方向长度选取120 m,整个模型的大小为长120 m,宽70 m,深40 m,如图1所示。但为了更好地与实测荷载数据对比,这里在DLOAD子程序中编制16节车厢运行。
地基、路基、轨道板结构均采用空间8节点实体单元模拟;动力边界采用三维黏弹性人工边界;轨道结构附近振动频率较高,模型阻尼考虑几何阻尼和瑞利材料阻尼,振动在传播过程中振动频率和振幅不断地衰减,因此出于提高计算效率的考虑,在划分单元网格时,考虑离轨道越近的地方网格越小,离轨道越远的地方网格尺寸越大,同时为了保证计算精度,除去钢轨和CA砂浆层外,依据文献[12]的研究成果,网格单元尺寸控制在0.275~2.5 m。有限元模型,如图1所示。

(a) 路堤和桩模型

(b) 整体三维模型
2.2 模型验证
为了验证本模型建模的合理性以及计算结果的准确性,选取距离单侧轨道中心14.2 m和35 m处的振动计算结果和实测结果进行对比,具体的振动加速度时程曲线,如图2和图3所示。

(a) 实测结果
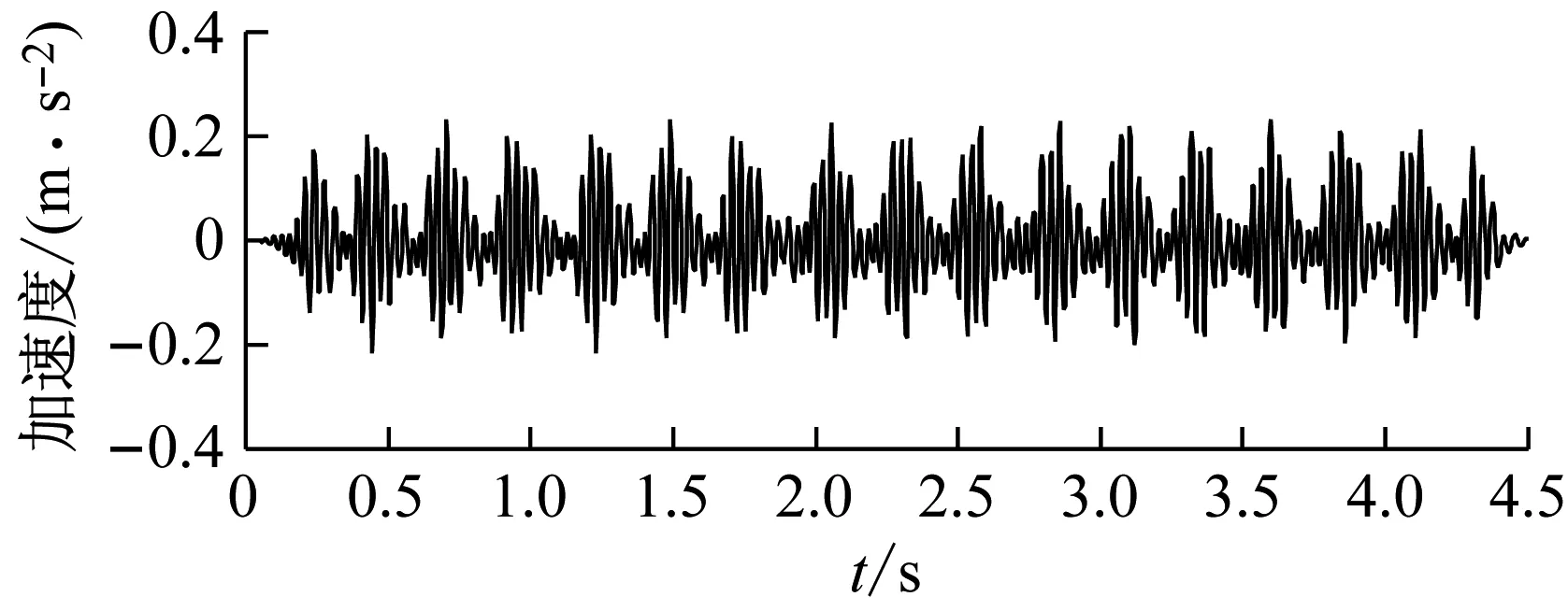
(b) 计算结果
Fig.2 Comparison of acceleration at a distance of 14.2 m away from track center
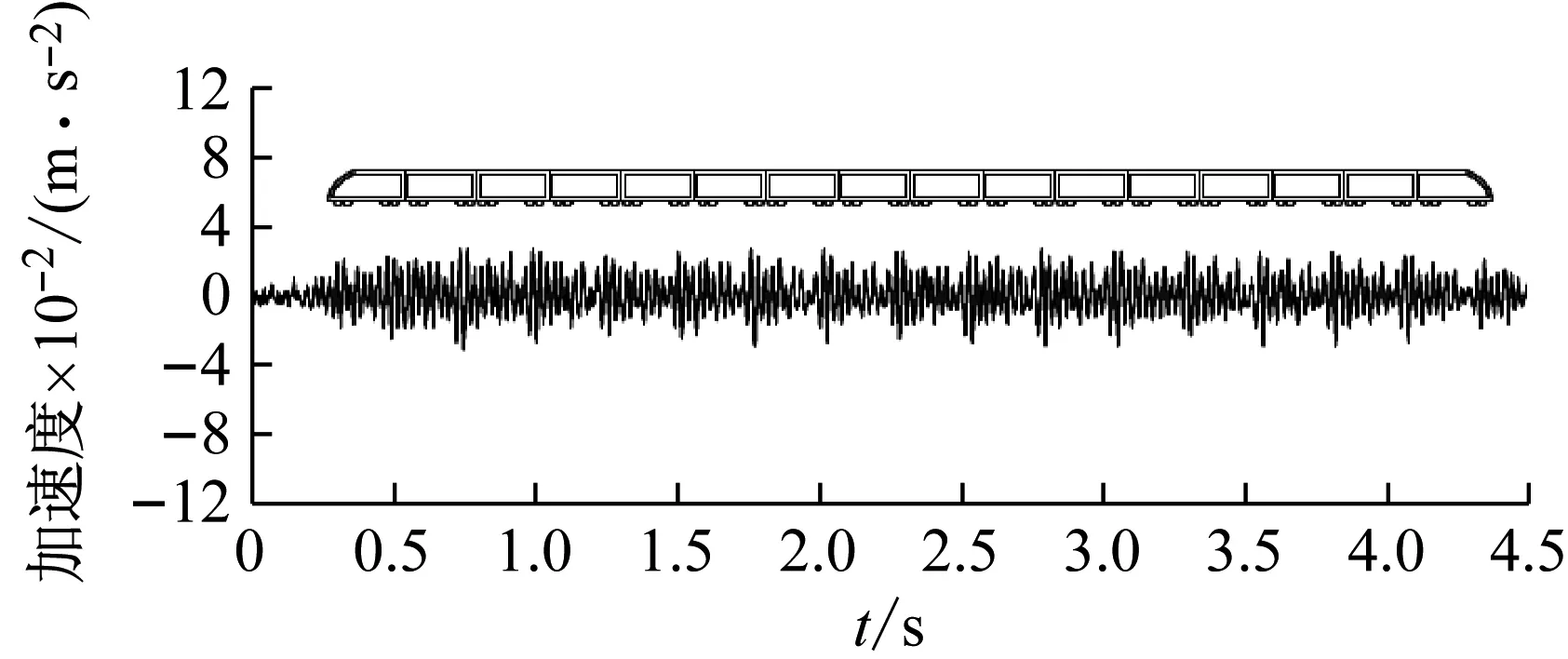
(a) 实测结果
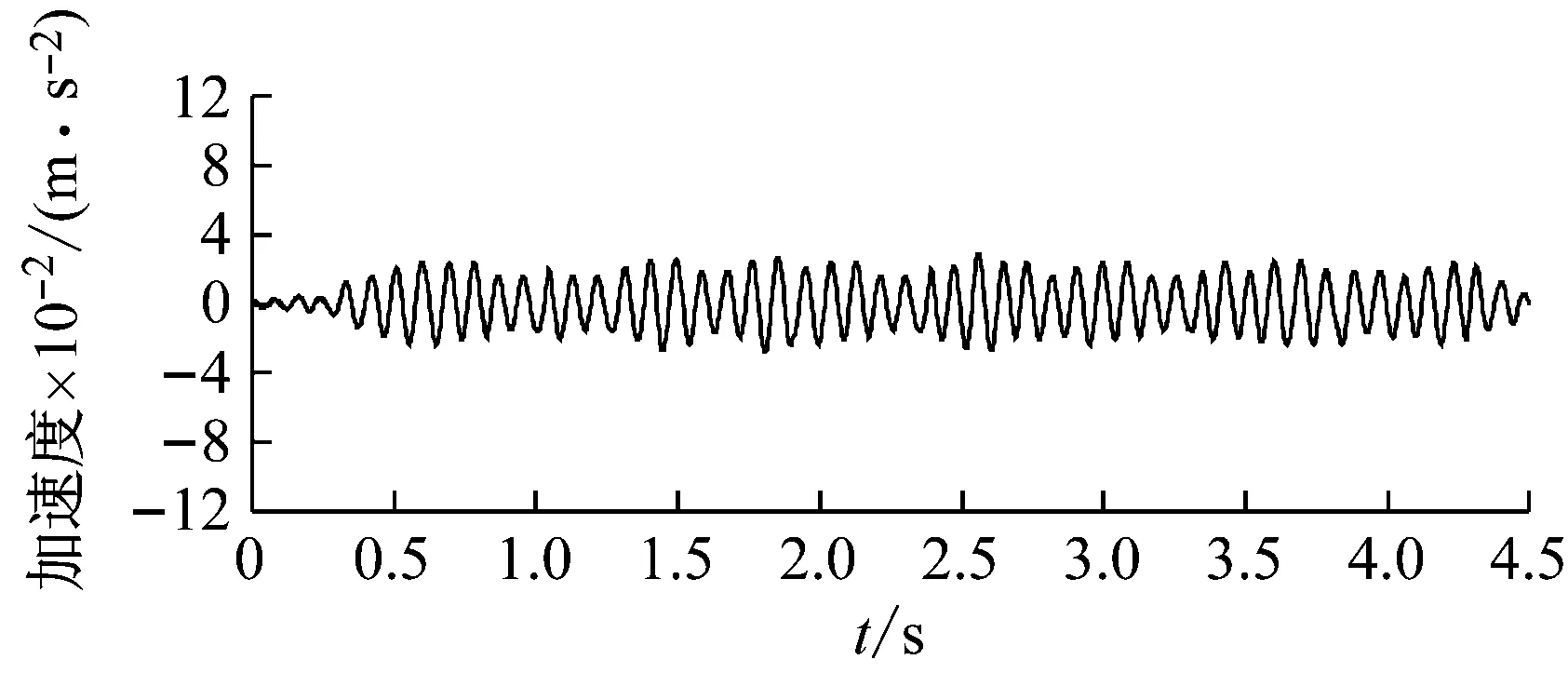
(b) 计算结果
Fig.3 Comparison of acceleration process at a distance of 35 m away from track center
由图2和图3可知:距离线路中心14.2 m处模型计算得到的加速度时程曲线与实测曲线较为一致,两者都能很好地反映高速列车通过时引起的地面波动,可见周期性轮对;振动幅值也较接近,且计算曲线与实测曲线的整体走势基本一致,均呈现出中部车厢轮对引起的振动峰值略高于两端部。在距离线路中心35 m处,模型计算得到的加速度时程曲线相对于实测曲线比较稀疏,看来数值模拟并不能全面考虑实际工况的所有因素。
总体而言,数值模拟和实测加速度峰值趋势接近,数值模拟能反应列车运行引起地面振动的主要因素。
图4为实测结果和模拟结果在与轨道中心不同垂直距离处地面加速度峰值的对比曲线。由图4可知,数值模拟与实测加速度峰值随距离衰减趋势吻合较好,均呈现从坡脚到距离线路中心30 m处快速衰减,超过30 m后加速度峰值衰减明显变慢,表明土体材料阻尼开始起主导作用。
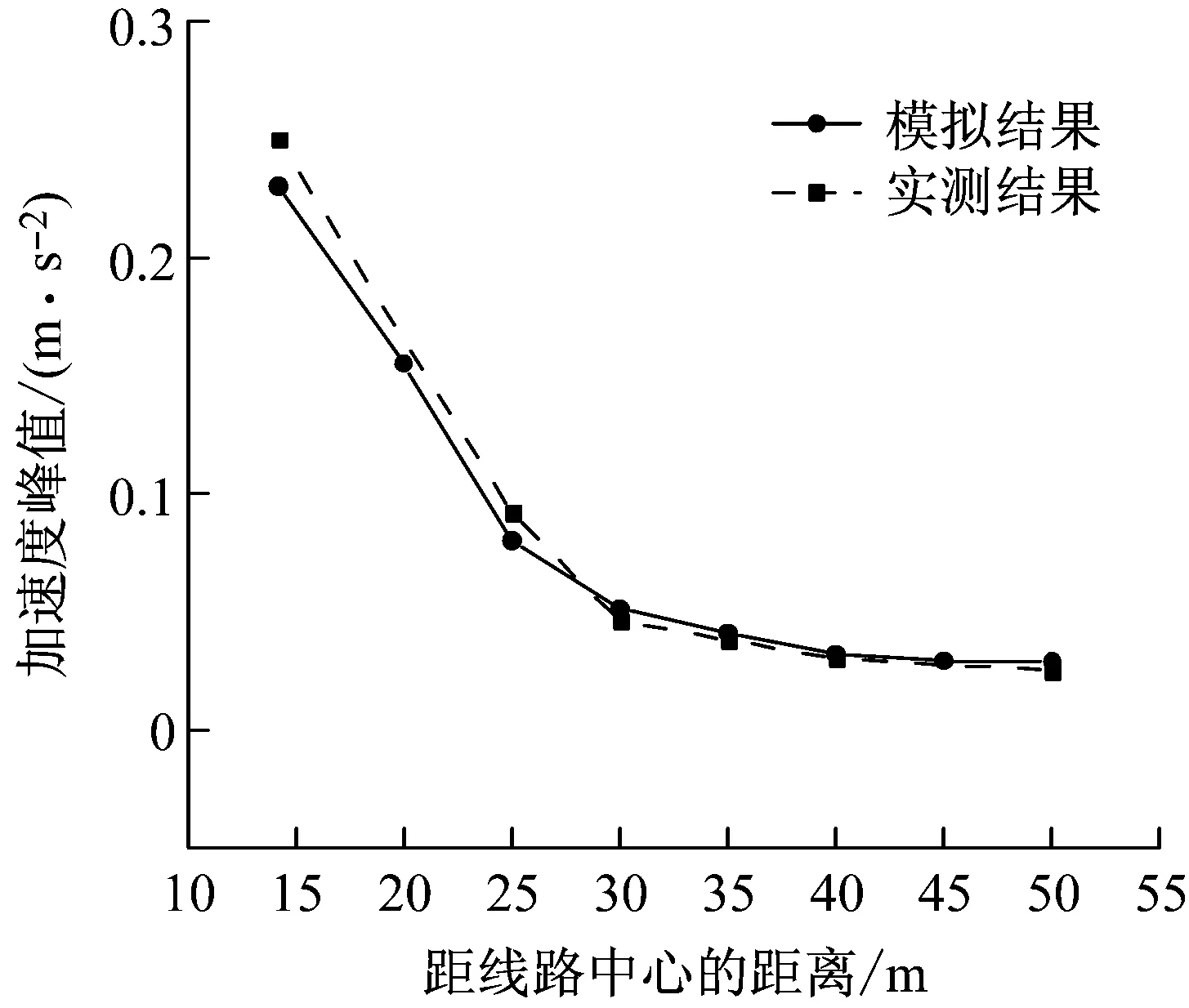
图4 与轨道中心不同距离处地面加速度峰值对比
Fig.4 Comparison of peak ground acceleration at different distance from track center
此外,加速度振级是评价环境振动的重要指标,因此为了进一步保证模型的合理性,还需要对模型和实测结果的加速度振级进行对比分析。图5为模拟结果和实测结果采用ISO2631-1:1997中的Wk计权方法得到的与轨道中心不同垂直距离处地面铅垂向Z振级的计算结果对比。由图可知,模拟结果和实测结果整体趋势吻合较好,两者之间的最大差异不超过5 dB,并且距离线路中心较近的测点环境振动差距较大,而较远处的差别越来越小。从不同距离的加速度振级对比结果可以看出,该模型能够较好的模拟计算高铁复合路基的环境振动。
3 桩网复合路基环境振动影响因素分析
3.1 计算模型及参数
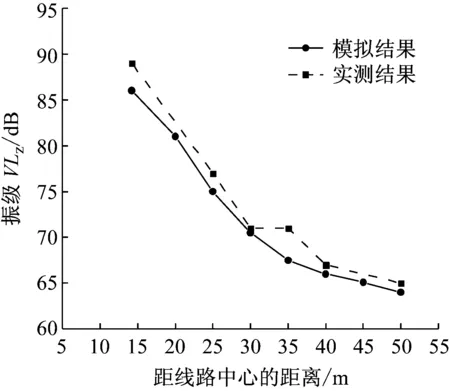
图5 与轨道中心不同距离处地面加速度振级对比
Fig.5 Comparison of ground acceleration vibration level at different distance from track center
高速铁路单线桩网复合路基横断面简图,如图6所示。地基选用长江下游冲积平原沉积软土,其主要分布在丹阳到常州之间的典型地基土。松软土及软土层多为深灰色游泥质粉质黏土、软黏土、黏土,呈软塑到流塑状态;表层为厚1~5 m硬壳层,局部达到8 m;下伏层为第四系上更新统黏土、粉土、粉砂、粉质黏土等。具体的路基参数,如表2所示。
参照“2”节的建模,列车荷载与轨道梁的相关参数与第2节相同,模型尺寸长120 m,宽70 m,深53.8 m,为减少计算量,这里在DLOAD子程序中编制4节车厢荷载运行分析,具体的三维有限元分析模型,如图7所示。
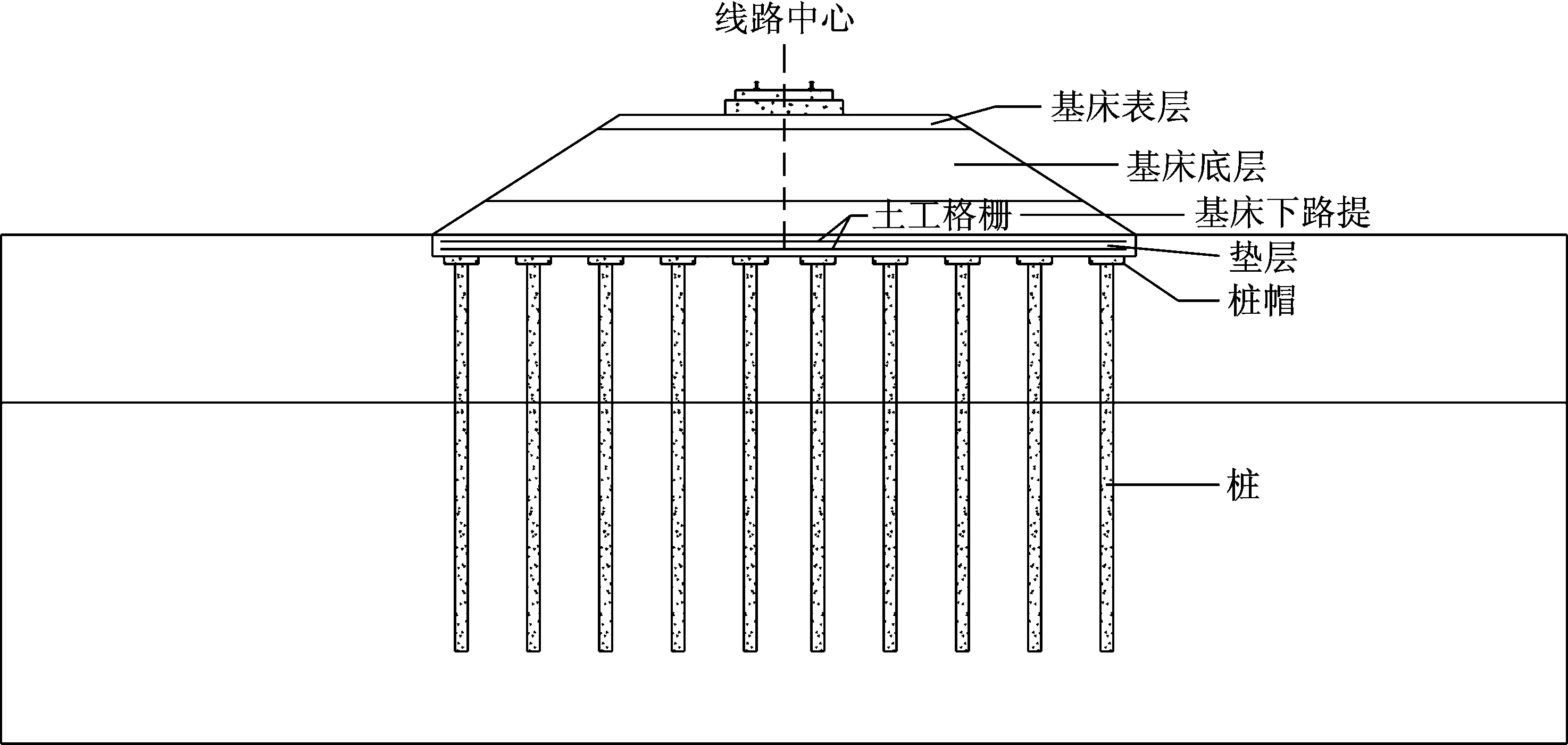
图6 单线高速铁路桩网复合路基剖面简图
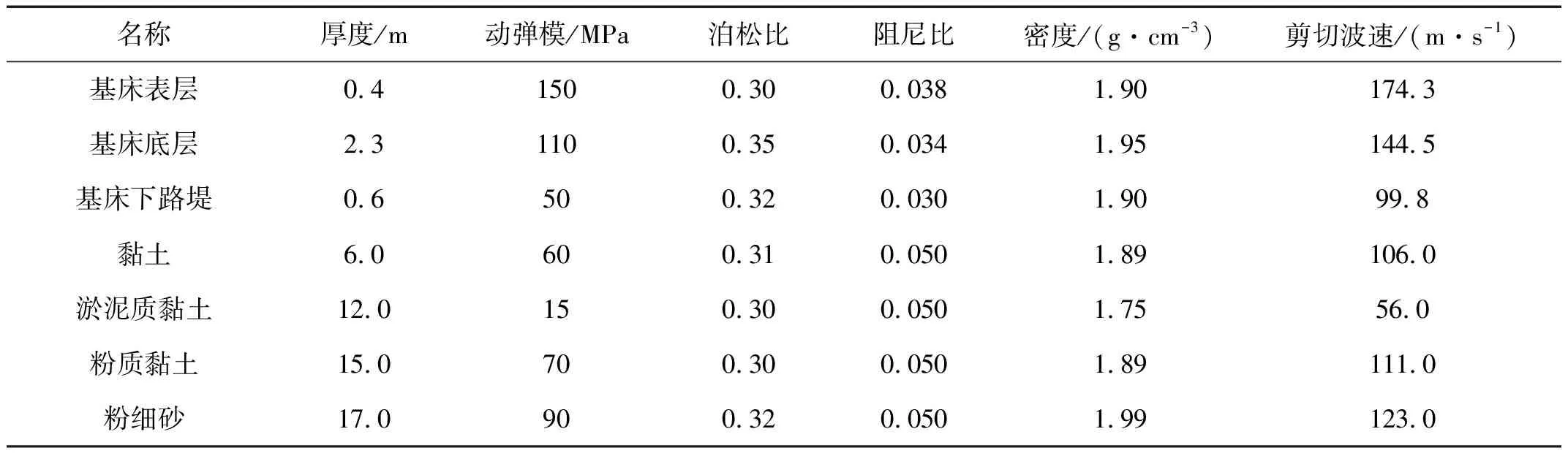
名称厚度/m动弹模/MPa泊松比阻尼比密度/(g·cm-3)剪切波速/(m·s-1)基床表层0.41500.300.0381.90174.3基床底层2.31100.350.0341.95144.5基床下路堤0.6500.320.0301.9099.8黏土6.0600.310.0501.89106.0淤泥质黏土12.0150.300.0501.7556.0粉质黏土15.0700.300.0501.89111.0粉细砂17.0900.320.0501.99123.0
CFG桩复合路基的桩长为18 m,桩径0.5 m,桩间距1.8 m,桩的动弹性模量取10 GPa,密度取2.5×103kg/m3,泊松比0.2,桩顶采用边长为1 m的正方形桩帽,厚度为0.4 m,阻尼比为0.06;垫层厚度取0.6 m,动弹性模量取120 MPa,泊松为0.3,阻尼比0.05。垫层区域考虑铺设两层土工格栅,并视为弹性材料,动弹性模量取40 GPa,泊松比0.2,密度为1 500 kg/m3,轴向抗拉强度为500 kN/m。
为了合理的划分网格,模型分别创建了轨道梁、路堤、垫层、土工格栅、桩帽区、桩体区及其他土体部分共7个部件,再通过绑定约束将每个部件连接起来。桩土复合路基三维有限元模型各部件组成及桩和桩帽的分布图,如图8所示。
3.2 车速对环境振动的影响
随着列车速度的增加,轨道不平顺等因素会加大车轮与轨道间的相互作用,从而引起轨道产生更大的振动,列车速度是影响环境振动的重要因素之一[13]。考虑到高速列车运行速度在200 km/h以上,选取了200 km/h、250 km/h、300 km/h、350 km/h、400 km/h五种车速来进行模拟研究。

(a) 桩和桩帽模型
(b) 整体三维模型
图9和图10分别为不同车速下加速度峰值与轨道中心垂直间距衰减和加速度峰值随车速的变化曲线。由图可知,在距离轨道30 m范围内加速度衰减较快,30 m以外衰减较慢,表明30 m内以体波和几何阻尼为主,30 m外以面波和材料阻尼为主[14];车速在350 km/h时加速度峰值有较大的增加,这是因为模型中地基表层土体的瑞利波速为99 m/s,与车速(97.2 m/s)接近。研究表明[15],当车速接近土体的瑞利波速时,因为共振产生相对较大的地面振动,故当车速增加到400 km/h时,距离轨道中心20~30 m地面振动幅值反而略低于车速350 km/h时,因此,近轨道中心20~30 m共振条件决定地面振动大小。
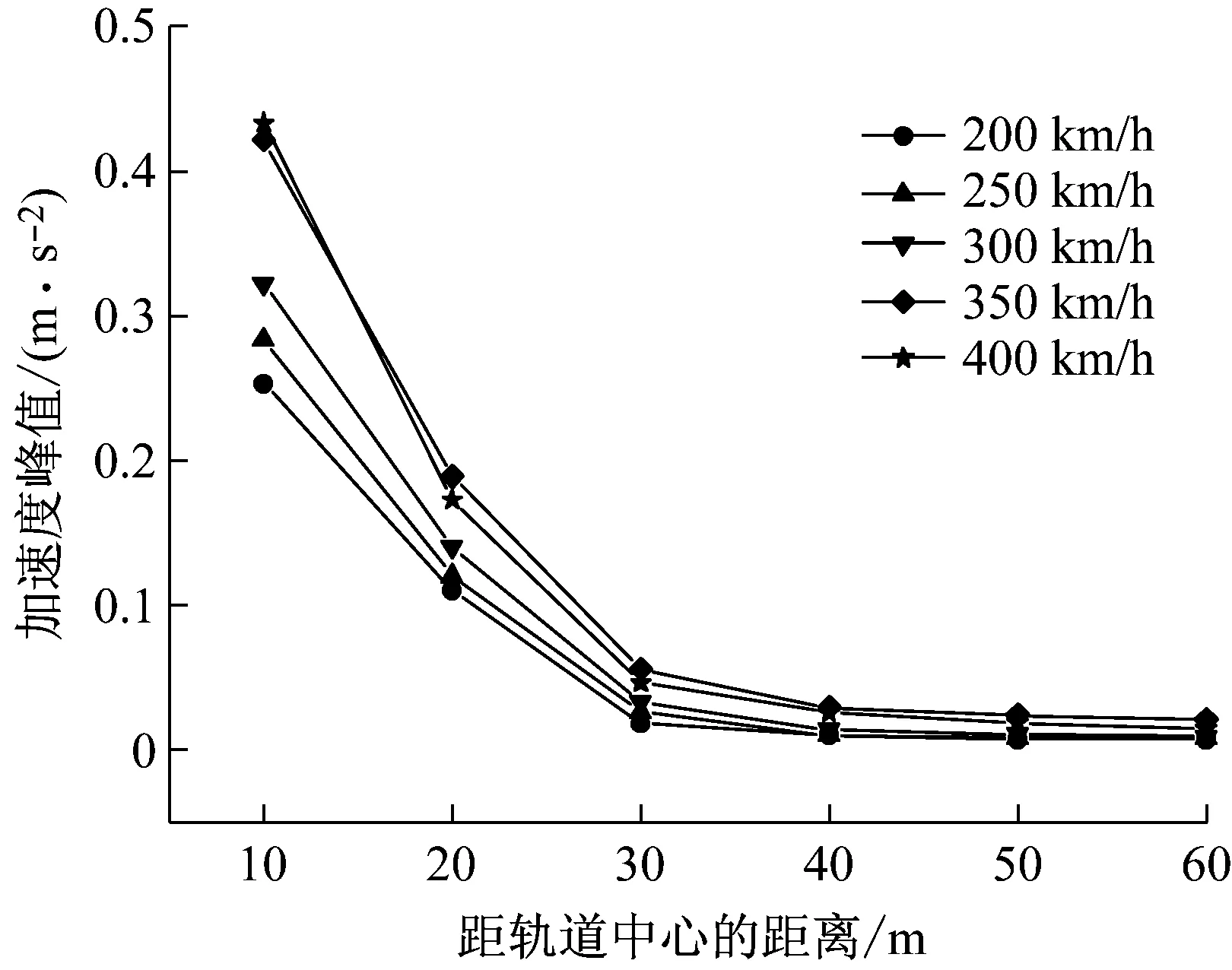
图9 不同速度下加速度峰值随距离衰减曲线
Fig.9 Attenuation curve of peak ground acceleration with distance at different speeds
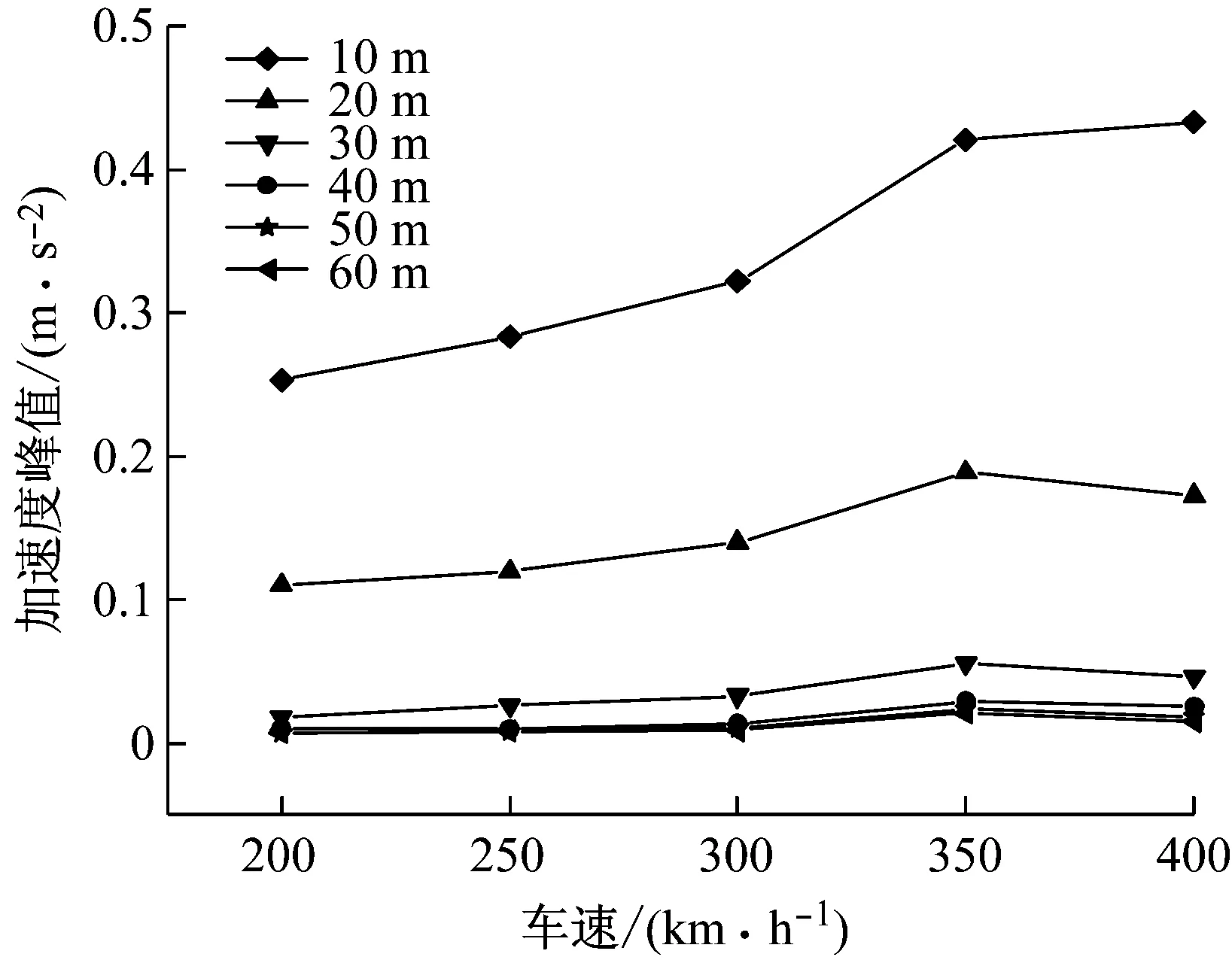
图10 不同距离处加速度峰值随车速的变化曲线
Fig.10 Variation curve of peak ground acceleration with speed at different distances
图11和图12分别为不同车速下加速度振级随与轨道中心垂直间距的衰减曲线和加速度峰值随车速的变化曲线。由图可知,当车速达到350 km/h时,由于接近土体的瑞利波速,地面加速度振级显著增加;当车速增加到400 km/h时,虽然在距离轨道中心30 m外加速度峰值较车速350 km/h时小,但随车速的增加,列车车轮与轨道产生更大的冲击,从而增加地面振动,因此,距轨道中心40 m及远处地面振动主要由车速决定,因此,必要时可限制车速,避免因高车速而产生大的环境振动。
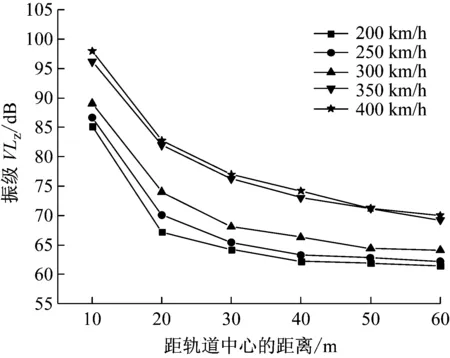
图11 不同车速下加速度振级随距离衰减曲线
Fig.11 Vibration level attenuation of ground acceleration with distance at different train speed
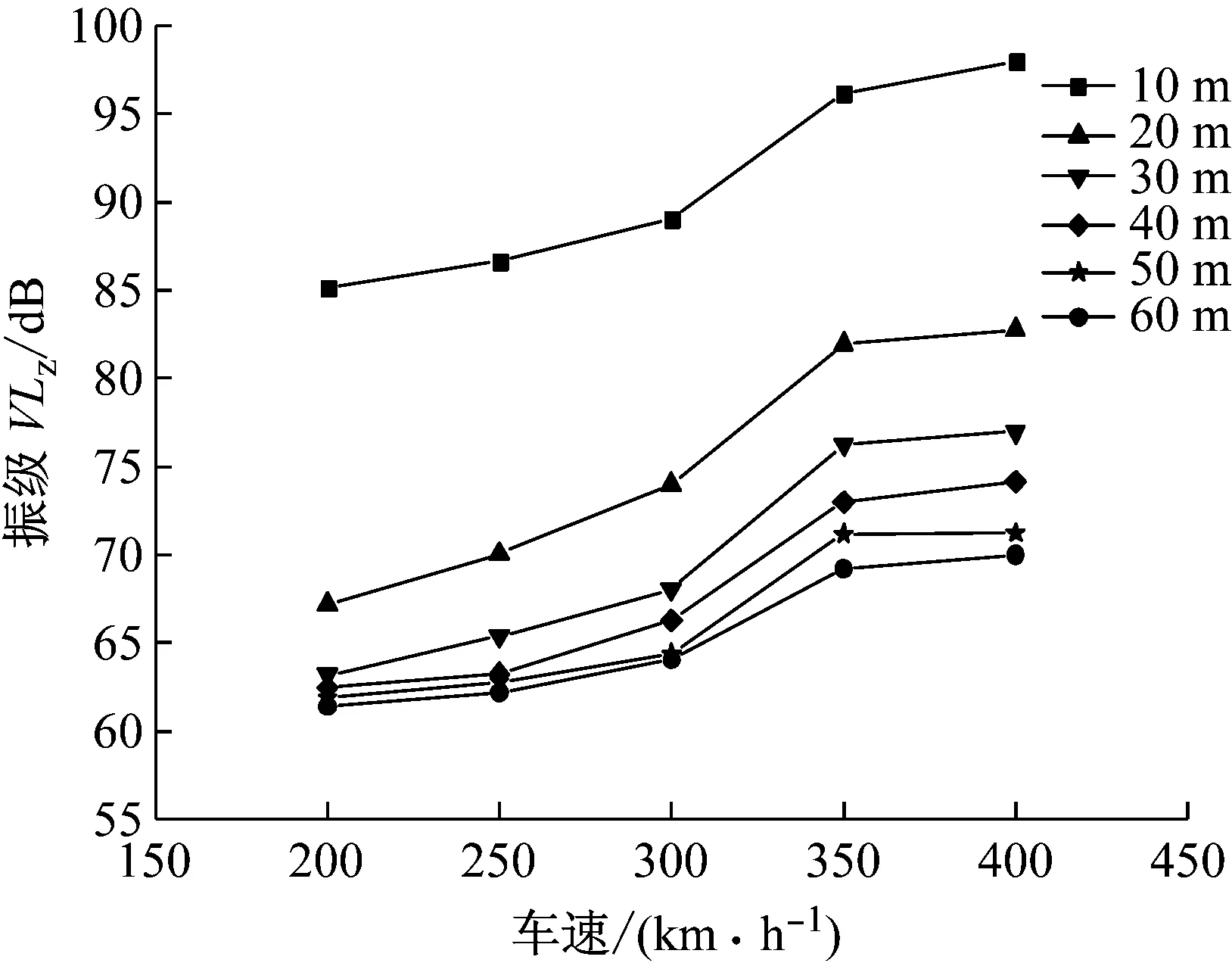
图12 不同距离处加速度振级随车速的变化曲线
Fig.12 Vibration level attenuation of ground acceleration with train speed at different distance
3.3 路堤高度对环境振动的影响
高速铁路为了适应沿途的地面起伏,往往会不断地调整路堤的填筑高度,随着路堤高度的不同,高铁运行引起的环境振动也将变化,为此选取了3.3 m、4.3 m、5.3 m、6.3 m四种路堤高度进行数值模拟。
图13和图14分别为不同路堤高度下加速度峰值随距离的衰减曲线及加速度峰值随路堤高度的变化。
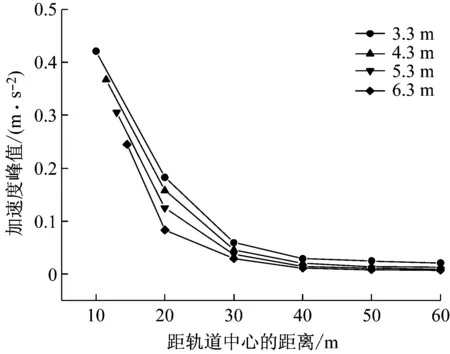
图13 不同路堤高度下加速度峰值随距离的衰减曲线
Fig.13 Attenuation curve of peak ground acceleration with distance at different embankment height
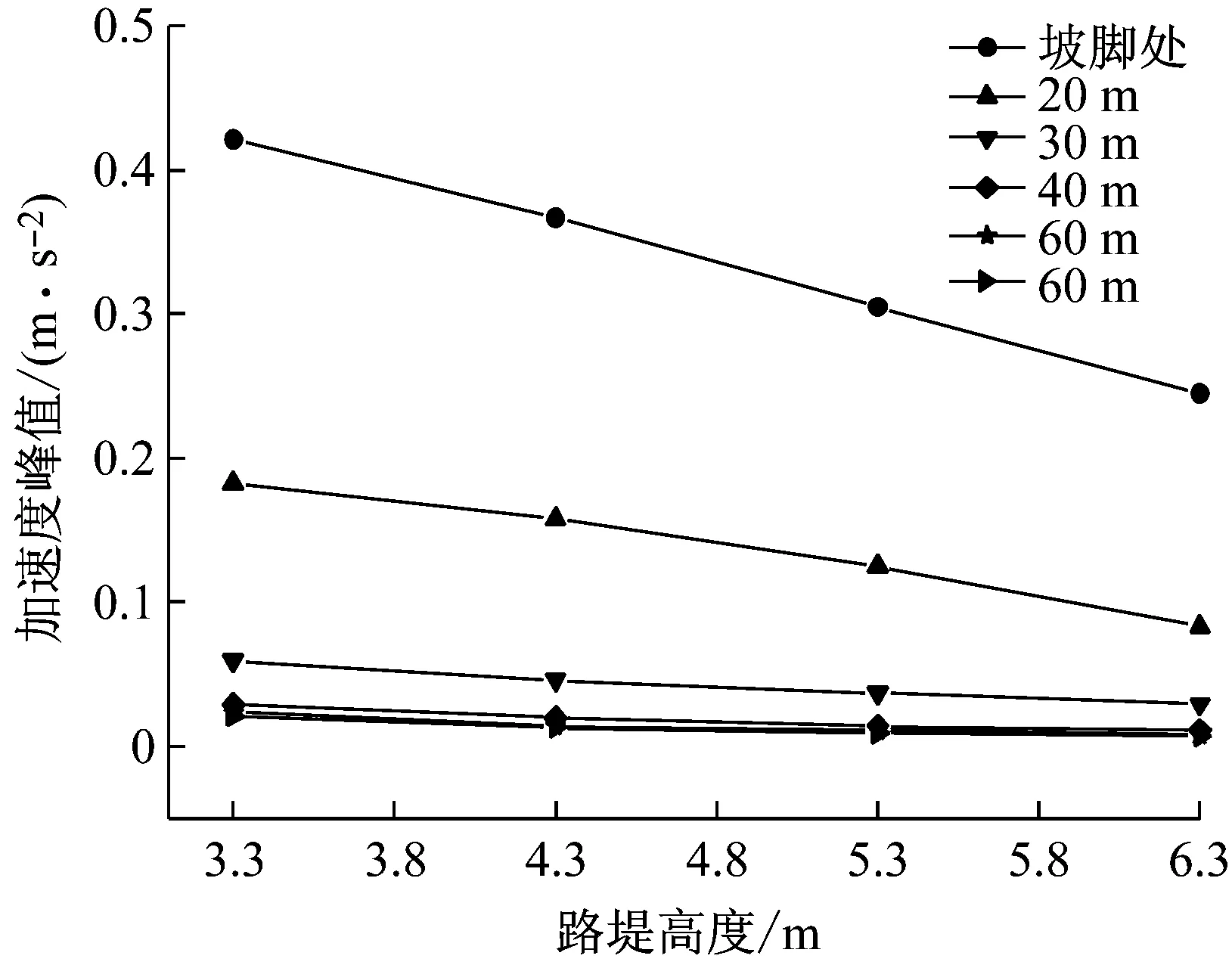
图14 不同距离处加速度峰值随路堤高度的变化曲线
Fig.14 Variation curve of acceleration peak with embankment height at different distances
由图可知,随着路堤高度的增加,加速度峰值减小,其中在路堤坡脚处加速度峰值减小较小,而在坡脚外到30 m之间加速度峰值减小较大,并且在距离轨道中心30 m外加速度峰值的绝对值减小较少,但相对值减小较大,表明随路堤高度的增加,对坡脚处的地面加速度峰值影响较小,而对远离坡脚处的振动影响较大。
图15和16分别为不同路堤高度下环境振动加速度振级随距离的衰减曲线以及地面加速度振级随路堤高度的变化曲线。由图可知,加速度振级的衰减规律和加速度幅值的衰减规律类似,不同路堤高度下路堤坡脚处的加速度振级减小量相对较少,而随着距离的增加,加速度振级随路堤高度的增加而减小的幅度较大,特别是>20 m处;当距离>30 m时,虽然不同路堤高度下加速度峰值的绝对量变化较小,但是相对量仍然变化较大,所以距离轨道中心30 m外不同路堤高度下加速度振级的变化仍然非常大;随着路堤高度的增加,同一位置的加速度振级减小幅度不断地增大,这是因为路堤高度越高,路堤下加固范围也越大,其对振动的衰减也越大。因此,当铁路沿线对环境振动有较高要求时,增大路堤高度是减小地面振动的有效措施之一。
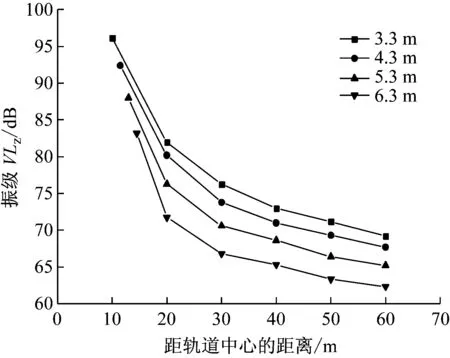
图15 不同路堤高度下加速度振级随距离的衰减曲线
Fig.15 Vibration level attenuation of ground acceleration with distance at different embankment height
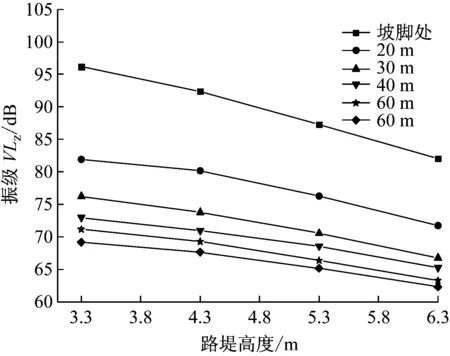
图16 不同距离处加速度振级随路堤高度的变化曲线
Fig.16 Vibration level attenuation of ground acceleration with embankment height at different distances
3.4 土体的材料阻尼比对环境振动的影响
土体的材料阻尼对振动的衰减有重要影响,而岩土工程材料的临界阻尼比的取值范围一般在2%~5%,因此分别选取阻尼比为2%、3%、4%和5%,分析了高铁复合路基地面加速度峰值和加速度振级的变化规律。
图17和图18分别为不同土体阻尼比情况下地面加速度峰值随距离的衰减曲线以及加速度峰值随阻尼比的变化规律。由图可知,不同土体阻尼比条件下,地面加速度峰值的衰减趋势较为一致,并且随阻尼比的增大,列车动荷载产生的振动加速度峰值越来越小;在距离路堤坡脚较近处,阻尼比的变化对加速度峰值的影响不明显,但随距离的增加,阻尼比的影响越来越大,这是因为阻尼比影响振动波在土体中的传播,并且这种影响随距离的增加会越来越明显。
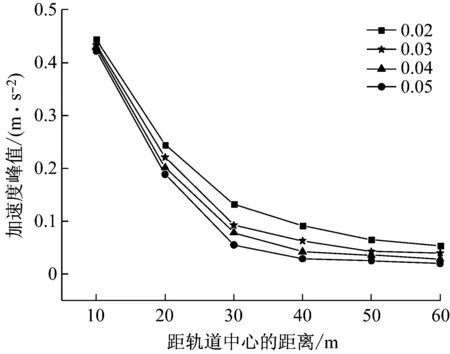
图17 不同土体阻尼比下加速度峰值随距离的衰减曲线
Fig.17 Attenuation curve of peak ground acceleration with distance at different soil damping ratio
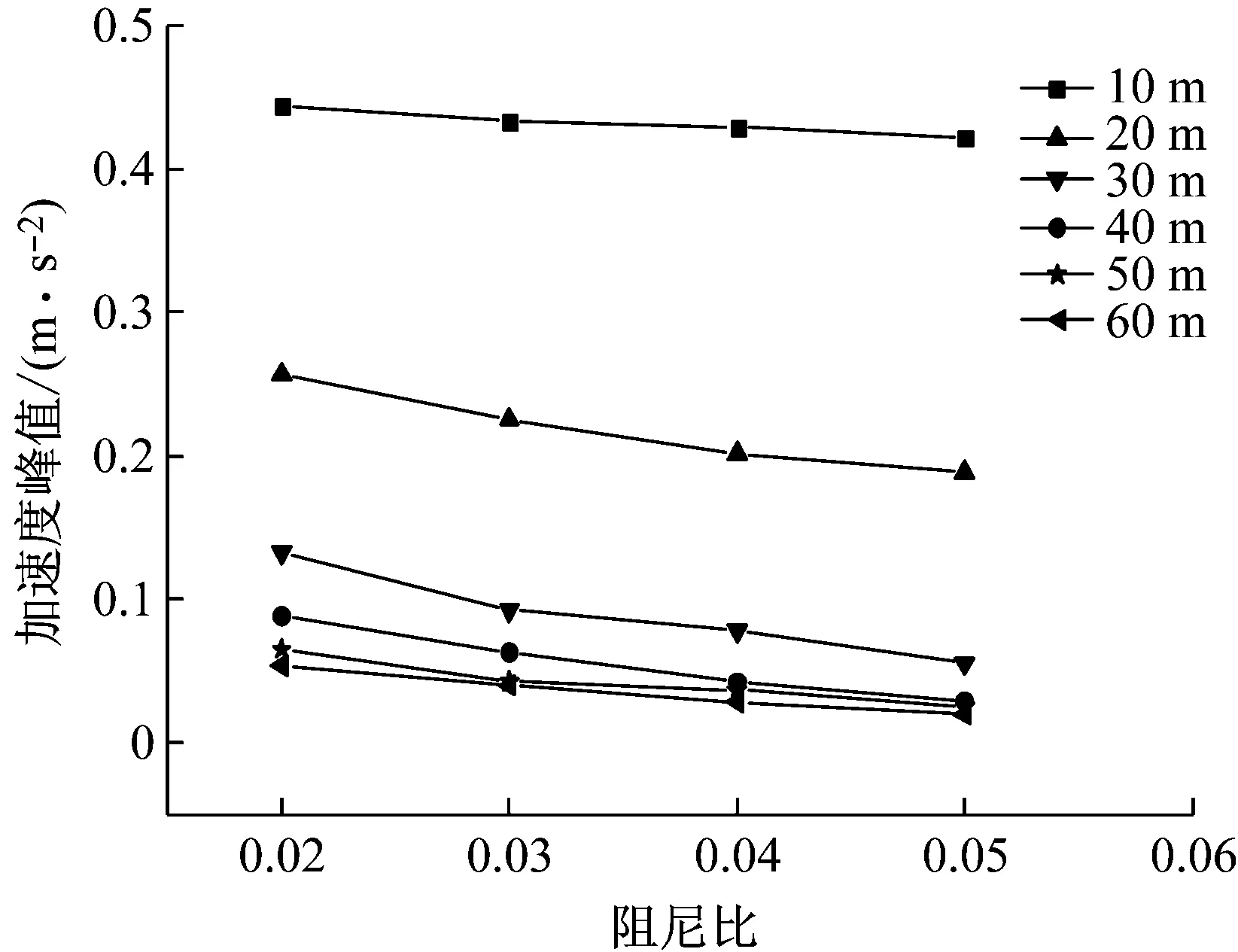
图18 不同距离处加速度峰值随阻尼比的变化曲线
Fig.18 Variation curve of peak ground acceleration with soil damping ratio at different distances
图19和图20分别为不同土体阻尼比情况下地面加速度振级随距离的衰减曲线以及加速度振级随阻尼比的变化规律。由图可知,随距离的增加,不同土体阻尼比条件下的地基加速度振级有类似的衰减规律;在距离线路中心10 m处,由于受到振动传播距离以及路堤的影响,不同阻尼比下的加速度振级变化不大;随距离的增加,阻尼比对振动的衰减影响越来越明显,因此不同阻尼比下加速度振级随距离的增加其差异也越来越明显。因此,只有准确获取地基土体的阻尼比,才能较好的预测高铁运行引起的路基远处地面环境振动大小。
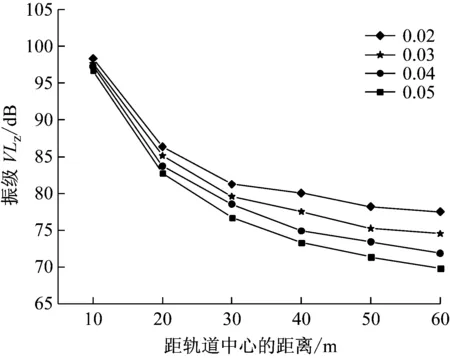
图19 不同土体阻尼比下加速度振级随距离的衰减曲线
Fig.19 Vibration level attenuation of ground acceleration with distance at different soil damping ratio
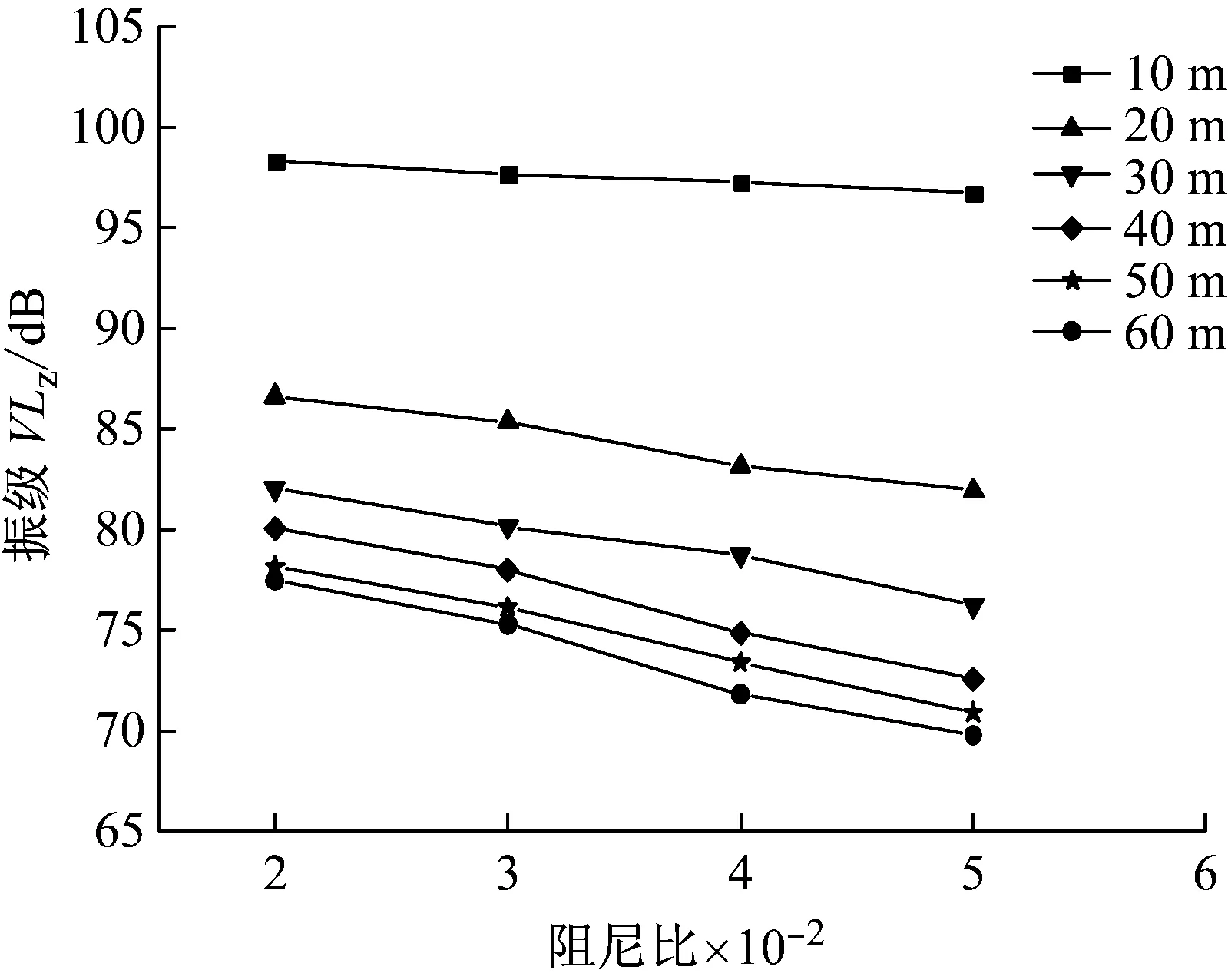
图20 不同距离处加速度振级随阻尼比的变化曲线
Fig.20 Vibration level attenuation of ground acceleration with soil damping ratio at different distances
4 结 论
本文建立包含垫层、桩帽、桩体的轨道-路堤-桩网复合地基三维有限元模型,分析了车速、路堤高度及土体阻尼比对高铁复合路基地面环境振动的影响。主要结论如下:
(1) 通过与高铁地面振动实测结果的对比,验证了本文模型能较为有效地模拟高速列车动荷载引起的地面振动。
(2) 随车速的增加,地面振动增大,当车速接近土体的瑞利波速时,产生共振效应,近轨道中心处,车速与路基土体的共振条件决定地面振动大小;距轨道中心远处,地面振动主要由车速决定,必要时可限制车速以减小环境振动。
(3) 路堤高度越高,复合路基中加固范围越大,对列车动荷载引起的地面振动减小越大,因为垫层和桩体将振动波能向路基深部传播。
(4) 土体的材料阻尼比决定路基远处地面振动,材料阻尼越大,地面振动随距离衰减越快,合理的获取地基土体的阻尼比对准确预测高速列车引起的地面环境振动有重要意义。
