基于信息熵优化变分模态分解的滚动轴承故障特征提取
2018-12-21李华,伍星,刘韬,陈庆
李 华, 伍 星, 刘 韬, 陈 庆
(昆明理工大学 云南省高校振动与噪声重点实验室,昆明 650500)
轴承是机械传动系统的核心部件[1],其故障是造成机械故障的重要原因之一。因此,对轴承的状态监测与故障诊断一直是机械设备故障诊断的热点[2]。
当滚动轴承发生故障时,其振动信号包含了大量的运行状态信息,表现为非平稳性和多分量性的调制信号,特别在故障早期,由于调制源弱,早期故障特征通常很微弱,并且受周围设备、环境的噪声干扰,导致早期故障特征频率难以提取、识别[3-4]。
故障诊断的关键是从原始信号中提取故障特征信号(故障特征频率)。Huang等[5]提出了经验模式分解,此方法具有自适应分解特性,对非平稳和非线性信号的处理具有较高的效率。因此,基于EMD(Empirical Mode Decomposition)的故障诊断方法层出不穷。但EMD存在模态混叠、端点效应、受采样频率影响较大等不足[6-7]。基于此,Dragomiretskiy等[8]提出了一种自适应信号处理新方法—变分模态分解(Variational Mode Decomposition,VMD),该方法通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽,相比于EMD,VMD将信号分解转化为非递归、变分模态分解模式并且具有坚实的理论基础,有效地弥补了EMD、EEMD(Emsemble EMD)等的不足。很多学者已将VMD应用于轴承故障诊断研究。Mohanty等[9]将VMD引入轴承故障诊断,并取得了比EMD更好的效果。刘长良等[10]提出了基于变分模态分解的故障特征提取方法,利用观察中心频率的方法确定模态个数,并采用模糊C均值聚类进行故障识别。赵洪山等[11]提出了基于变分模态分解和奇异值分解的故障特征提取方法,利用峭度指标选取敏感IMF(Intrinsic Mode Function),对选取的IMF进行奇异值分解重构,取得良好效果。唐贵基等[12]提出了基于包络谱特征因子的影响参数自动搜寻策略,并成功实现轴承故障诊断。
当滚动轴承发生故障时,由于振动信号表现出的幅值调制特性[13],通过包络分析可以得到轴承的故障特征频率。本文提出信息熵优化VMD的轴承故障特征提取方法。针对模态K和惩罚因子α,提出了基于信息熵最小值的确定方法。首先,利用VMD对原始信号进行分解,利用信息熵最小值原则确定[K,α],然后,选取利用上述优化过程中获得的信息熵最小值所在的IMF为有效IMF;最后,对选取的IMF分量进行包络解调分析,提取轴承故障特征频率。
1 基础理论
1.1 变分模态分解(VMD)
变分模态分解(VMD)是一种基于维纳滤波的自适应信号处理新方法。在VMD算法中,每一个IMF均被称为AM-FM信号,即
uk(t)=Ak(t)cos(φk(t))
(1)
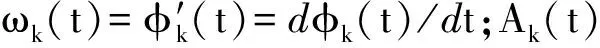
VMD的求解过程是一个变分问题的求解过程。假设每个模态是具有中心频率的有限带宽,中心频率和带宽在分解过程中不断更新,则,变分问题可表示为寻求k个模态函数uk(t),并使得所有模态函数的估计带宽和最小,模态之和为输入信号f。具体步骤如下:
步骤1 对每个模态函数uk(t)进行Hilbert变换
(2)
步骤2 对每个模态解析信号预估中心频率e-jωkt进行混合,将每个模态的频谱转移至基带
(3)
步骤3 利用H1高斯平滑估计移频后解析信号的带宽,得到如下受约束的变分问题
(4)
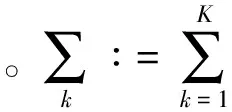
步骤4 为求取上述变分问题,引入二次惩罚因子α和Lagrange乘法算子λ(t),二次惩罚因子α可在高斯噪声存在的情况下保证信号的重构精度,Lagrange乘法算子保证约束的严格性。扩展的Lagrange表达式如下
Γ({uk},{ωk},λ)∶=
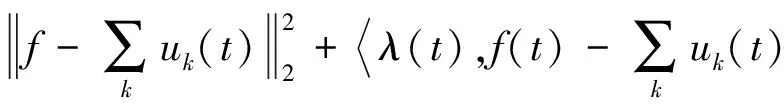
(5)
通过反复迭代,寻找Lagrange表达式的“鞍点”求解最小值,获得最优解。最优解即为本征模态函数{uk}及各自的中心频率{ωk}。
1.2 信息熵
假设一个随机序列x(n)=(x1,x2,…,xn)含有N个可能值,取得这些值的概率分布为P=(p1,p2,…,pn),则序列的信息熵为[14]
(6)
信息熵是描述系统不确定程度的物理量。当概率分布P的不确定度越大时,其对应的熵值就会越大;反之,当P的不确定度越小时,其熵值也越小。因此,若分解得到的IMF包含故障信息,由于周期冲击的缘故,其表现的越有序,导致熵值小。基于此,本文利用信息熵优化VMD并利用其选取包含故障信息的IMF分量。
2 基于信息熵优化VMD的故障特征提取
针对滚动轴承早期故障诊断中故障特征微弱难以提取的问题,提出了基于信息熵优化VMD的故障诊断方法。
2.1 基于信息熵的参数优化
因为当滚动轴承发生故障时,其故障表面会与其他元件周期性接触,发生周期性的撞击,从而产生周期性均匀脉冲冲击,可以认为此时信号越有序,所以致使信息熵值更小。因此,可将信息熵作为故障的一种表征,当存在信息熵值具有最小值时,可认为此时具有良好的VMD分解效果。基于此,本文提出了基于信息熵最小值原则确定VMD参数的方法。根据唐贵基等对于参数的讨论,可以先给定α的值,利用信息熵最小值确定模态K,然后以优化的K,再优化α。方法简单,且能达到良好的效果。其具体步骤及流程在“2.2”节中给出。
2.2 算法步骤及流程
本文提出的基于信息熵优化VMD的故障特征提取方法,旨在利用VMD优于EMD的性能,从原始信号中提取出包含故障特征的信号分量,进而实现微弱故障特征信息的提取。其诊断流程图,如图1所示。
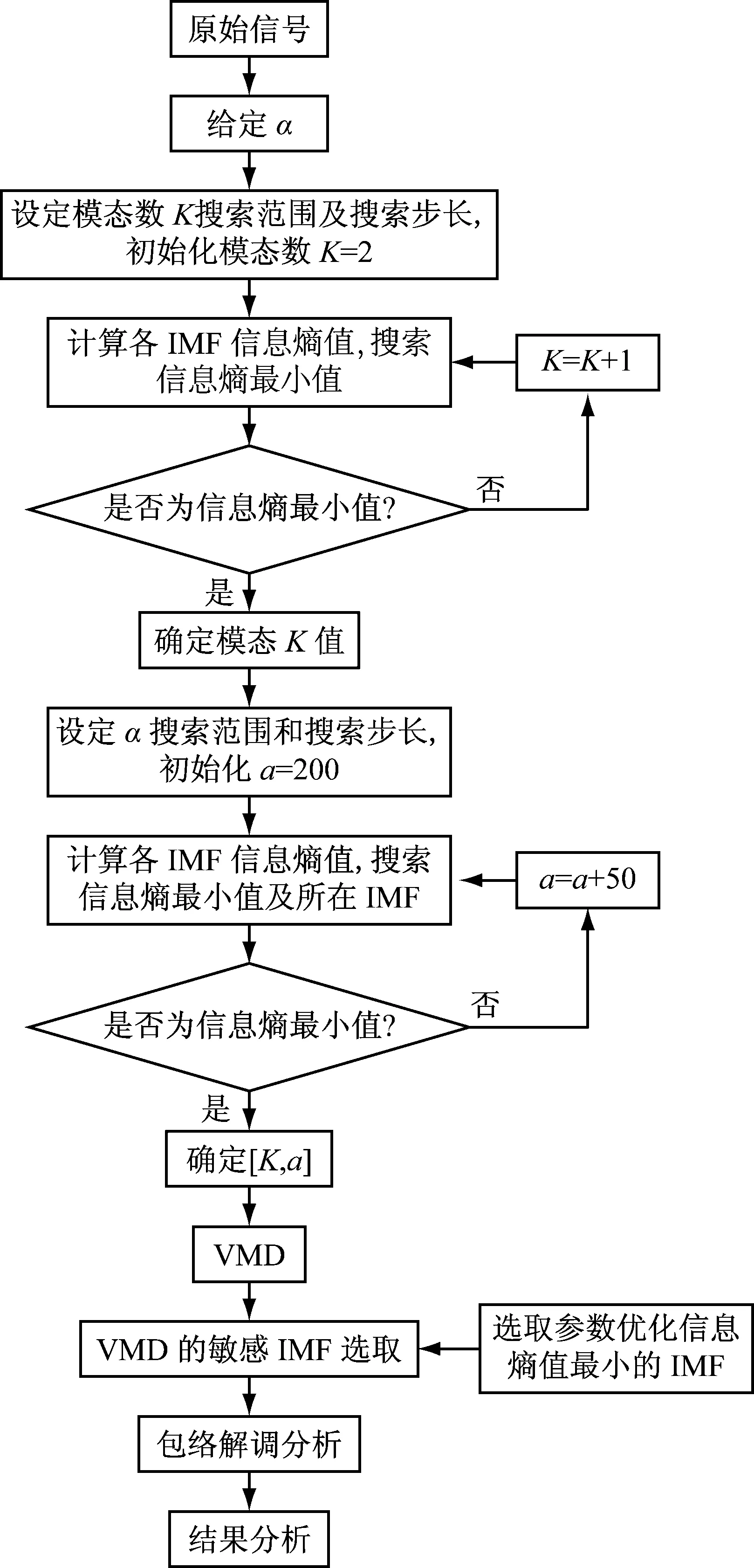
图1 诊断方法流程图
具体步骤如下:
步骤1 首先优化模态数K。初始化模态数K=2,惩罚因子α和带宽τ使用默认值:α=2 000,τ=0;对原始振动信号进行VMD分解,计算各个模态的信息熵,判断是否是信息熵最小值?如果是,则确定模态数K=K;如果不是,则K=K+1继续以上分析,直到取到信息熵取最小值为止。根据文献[12],需选取合适的K,本文选定K的搜索范围[2,16],步长为1。
步骤2 然后优化惩罚因子α。利用步骤1中确定的模态数K对α进行基于信息熵最小值原则的优化。原理与K的优化确定相同,直到搜索到信息熵最小值为止,确定最优α。因此获得最优[K,α]。设定α的搜索范围[200,2 000],步长为50。
步骤3 对原始振动信号进行基于上述优化[K,α]的VMD分解,得到相应的IMF分量,并且可获得熵最小值所在的IMF分量。
步骤4 选取上述分析所获得的信息熵值最小的IMF分量作为最佳的IMF分量用于进一步的分析处理。
步骤5 对步骤4中选取的IMF分量进行包络解调分析,将轴承故障理论特征频率与包络谱进行比较,判定轴承运行状态。
3 信号仿真分析
为了验证本文方法的有效性,本文利用轴承内圈故障的仿真信号进行分析,首先信息熵优化参数,通过VMD分解为既定数目的模态,然后再利用信息熵最小值选取敏感IMF,包络解调。滚动轴承的仿真信号可通过式(7)得到[15]
(7)
这里,系统采样频率fs为12 000 Hz,结构共振频率fn为3 000 Hz,内圈故障频率fi为79 Hz,转频fr为28 Hz,阻尼比B为500。为了验证算法的有效性,添加了信噪比为-6 dB的随机噪声。仿真信号时域图,如图2(a)所示,由于噪声影响,无法提取冲击特征。从图2(b)的包络谱可知,虽然可以提取故障特征,但都被噪声包围。因此,有必要进行处理,提高信号信噪比。
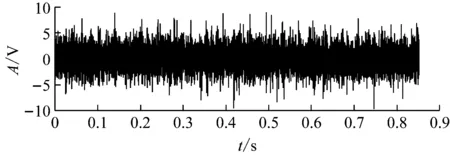
(a) 内圈故障时域波形
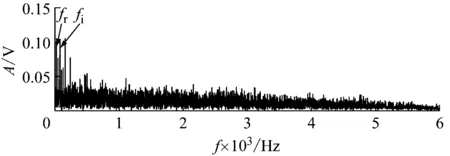
(b) 内圈故障包络谱
3.1 VMD参数优化
由于原始信号受噪声影响严重,因此,对信号进行VMD分解,初始化K=2,设定K的搜索范围为[2,16],利用信息熵最小值原则优化模态K。经过分析,当K=10时,取得熵最小值为0.558 0,所以取模态数为K=10。模态数与峭度最大值关系图,如图3所示。
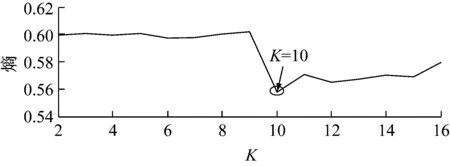
图3 模态数K与峭度最大值的关系
同样地,取定K=10,按照“2.2”节中设定的搜索范围及步长,优化惩罚因子α。可知,当α=650时,具有熵最小值0.552 9。惩罚因子α与峭度最大值的关系,如图4所示。因此,确定最优参数组合为[10,650]。
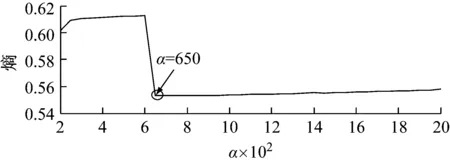
图4 惩罚因子α与峭度最大值的关系
3.2 VMD分析及IMF选取
对仿真信号进行处理,原始信号经信息熵优化的VMD分解后得到10个IMF分量,时域波形,如图5所示(仅给出了前8个IMF分量的时域波形)。为了便于后续分析,需要从中筛选出包含丰富故障特征信息的IMF分量。通过观察,各个IMF分量的差别不大,不能直观的判定哪一分量包含的故障特征信息最明显。
在上述参数优化过程中,可知IMF5的信息熵具有最小值0.552 9。如表1所示,给出各个IMF分量的信息熵值,由于篇幅限制,仅给出前六个IMF分量的信息熵。因此,选取IMF5为最佳分量,并进一步进行包络解调分析。

表1 各IMF的信息熵
IMF5的包络谱,如图6所示。从包络谱中特征频率fi及二倍频2fi、三倍频3fi以及转频fr均能明显地提取出来。表明本文所述方法能够从信噪比较低的原信号中有效提取出包含丰富故障特征信息的信号分量,进而实现故障特征频率的准确提取。








图5 VMD分解结果
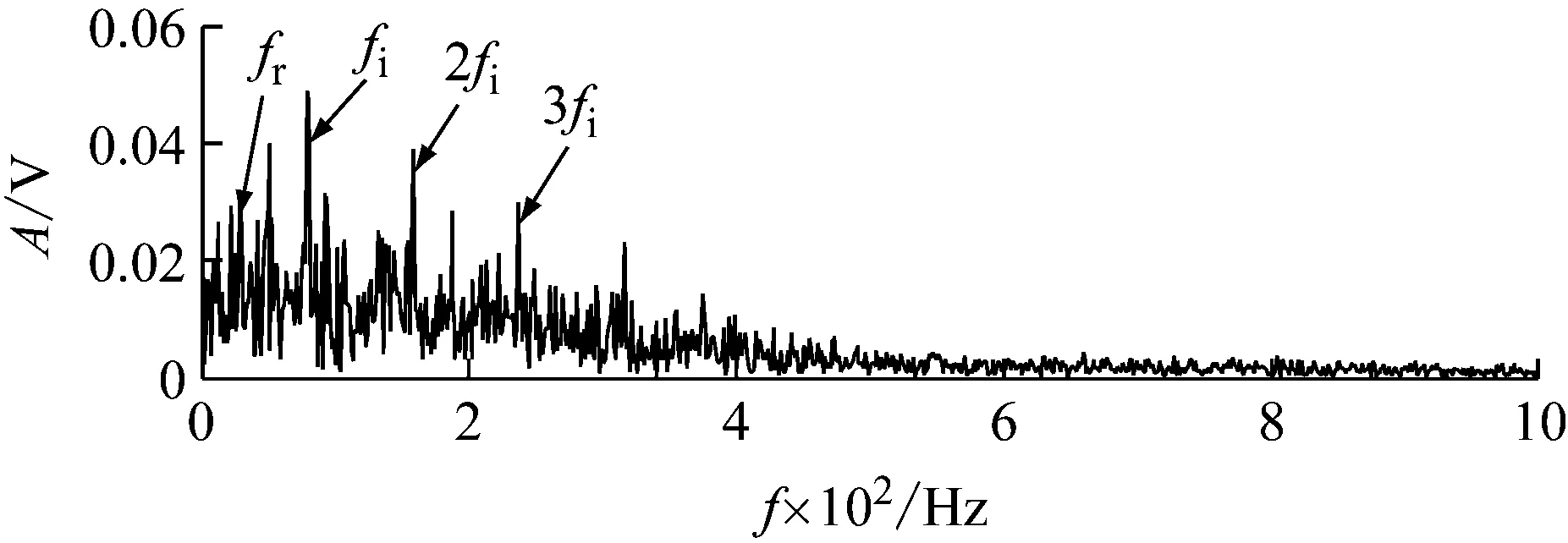
图6 IMF5包络谱
为了验证本文方法的优势,利用EMD对上述仿真信号进行分析,并选取信息熵最小的IMF进行包络解调分析。经EMD分解后得到13个IMF分量,分析可知,IMF2的信息熵值最小(0.659 3),故选取其进行包络解调分析,其时域波形和包络谱,如图7(a)、图7(b)所示。
从时域图7(a),虽然能看到部分冲击特征,但由于噪声影响,冲击很不明显,相比于图5中的IMF5的时域波形,IMF5能够明显看到脉冲冲击特征。从包络谱图7(b),虽然提取出故障特征频率,但与图6相比,背景噪声很严重,而且无法提取倍频及转频成分,分析效果很差。
4 实验验证及分析
4.1 外圈故障分析
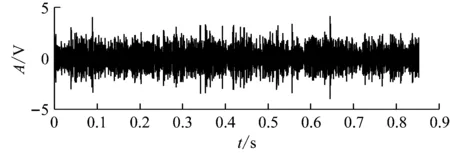
(a) IMF2时域波形
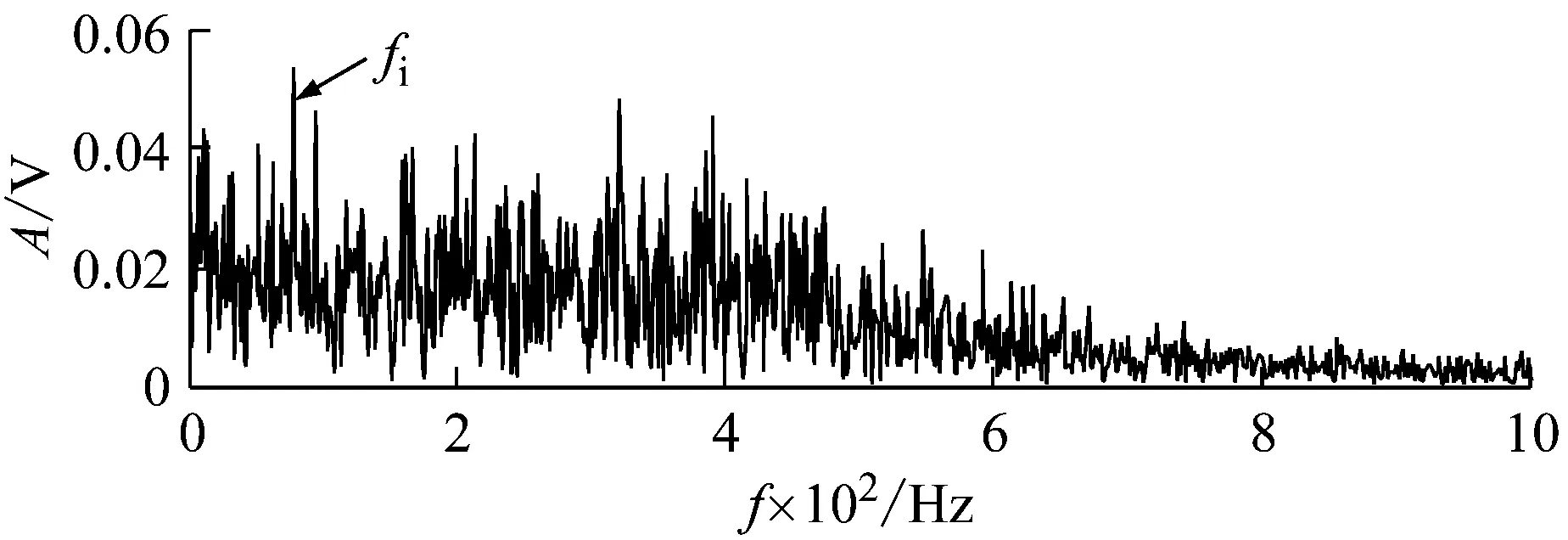
(b) EMD分解的IMF2包络谱
为验证本文方法的有效性,将其用于实际数据分析。本文采用来源于美国西储大学的轴承数据[16],轴承的型号为6205RS JEM SKF,采样频率fs=12 000 Hz,试验数据选择转速为1 797 r/min,负载为0,驱动端轴承在外圈故障状态下的数据,取8 000个数据进行分析。
表2所示为计算得到的轴承转频(fr)和外圈故障状态下故障特征频率(fo)。

表2 转频和特征频率
如图8(a)、图8(b)分别是轴承外圈故障数据的原始信号时域波形和包络谱。时域图中由于存在噪声的影响,无法清晰地提取冲击特征;包络谱中,虽然能够提取故障特征频率,但受到很严重的噪声影响,比如2 000~3 000 Hz附近存在明显的波峰,无法判别。
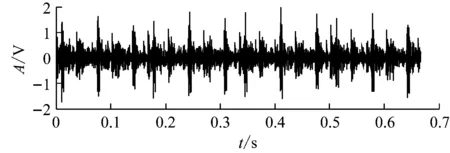
(a) 外圈故障时域波形
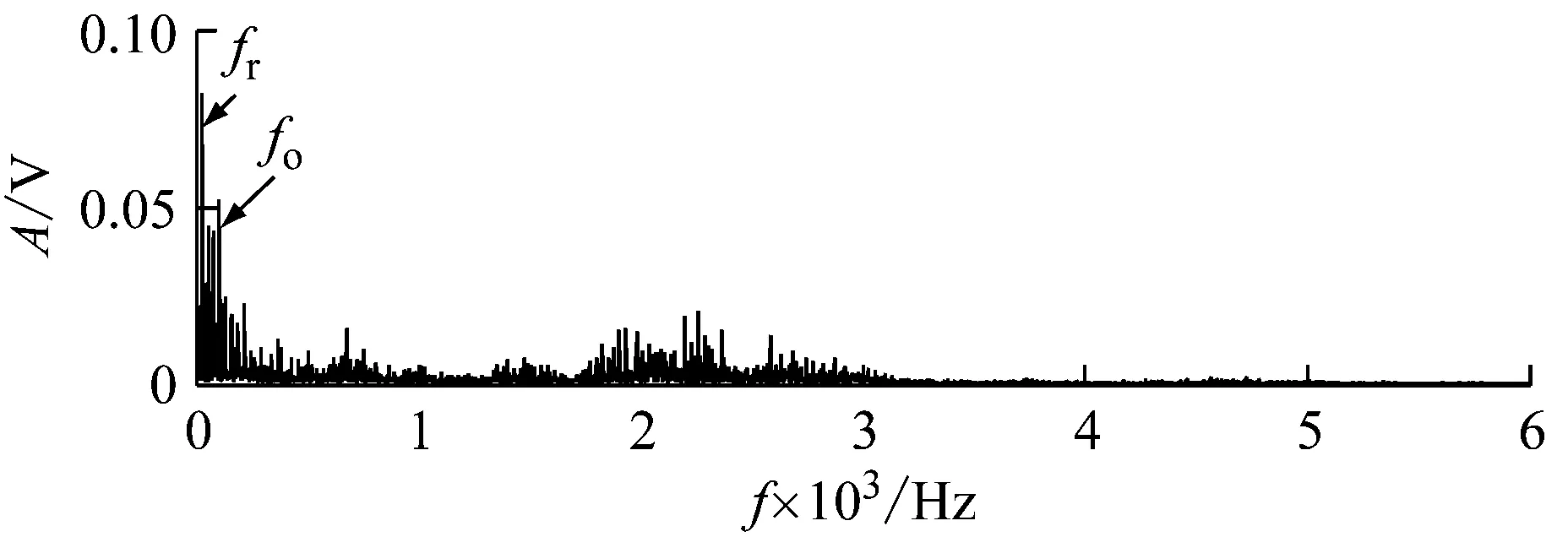
(b) 外圈故障包络谱
4.1.1 VMD参数优化
以下利用本文所述方法对轴承外圈故障信号进行分析。首先优化模态数K,模态数与熵最小值的关系,如图9所示。经过分析,当K=15时,取得熵最小值为0.519 5,所以取模态数为K=15。
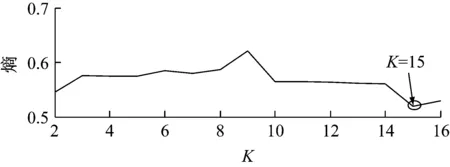
图9 模态数K与熵最小值的关系
同样地,取定K=15,按照“2.2”节中设定的搜索范围及步长,优化惩罚因子α。经分析可知,当α=1 950时,具有熵最小值0.514 9。α与熵最小值的关系,如图10所示。由此,可得最优参数组合[15,1 950]。
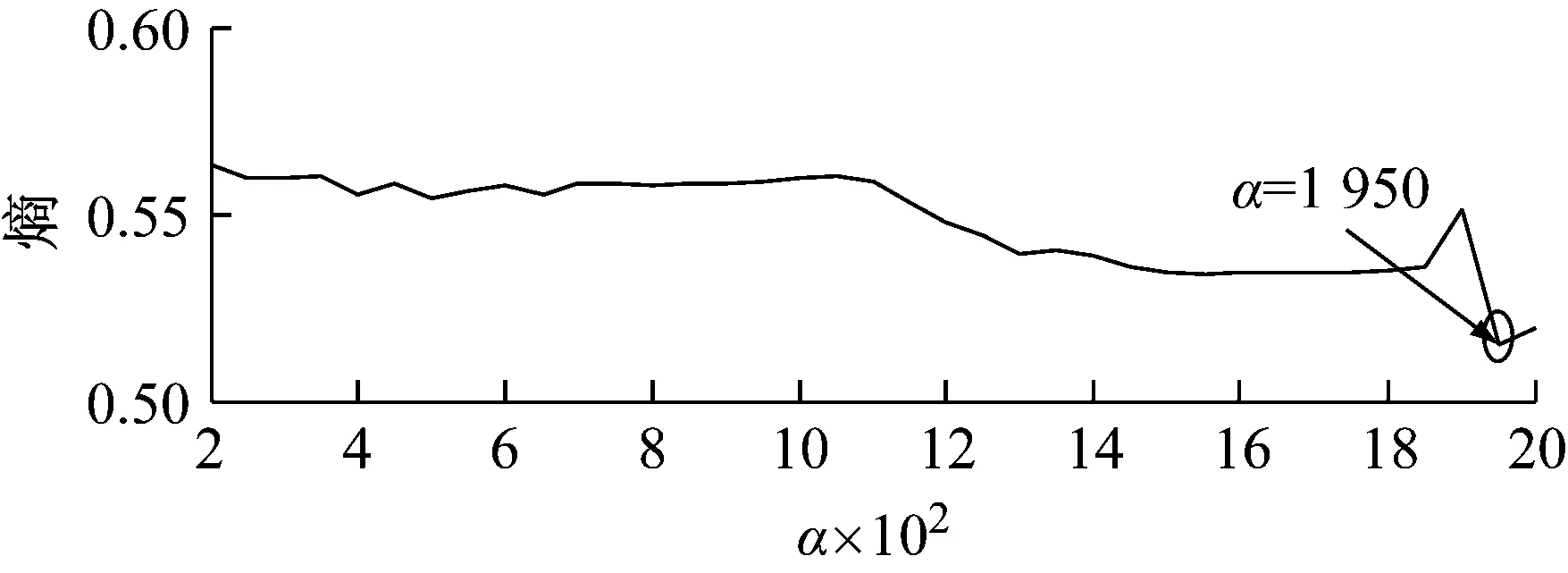
图10 惩罚因子α与熵最小值的关系
4.1.2 VMD分析及IMF选取
对外圈故障信号进行VMD分解,得到15个IMF分量,由“4.1”节的参数优化过程,可得各个IMF的信息熵,如表3所示(由于篇幅限制,这里仅给出IMF11~IMF14的熵值)。IMF13的信息熵具有最小值,因此选取IMF13进行包络解调分析。

表3 IMF11~IMF14的信息熵
对IMF13进行包络解调分析,如图11所示。由包络谱可以清晰地提取出外圈故障的故障特征频率fo及其转频fr,由此便可以判定轴承外圈故障。
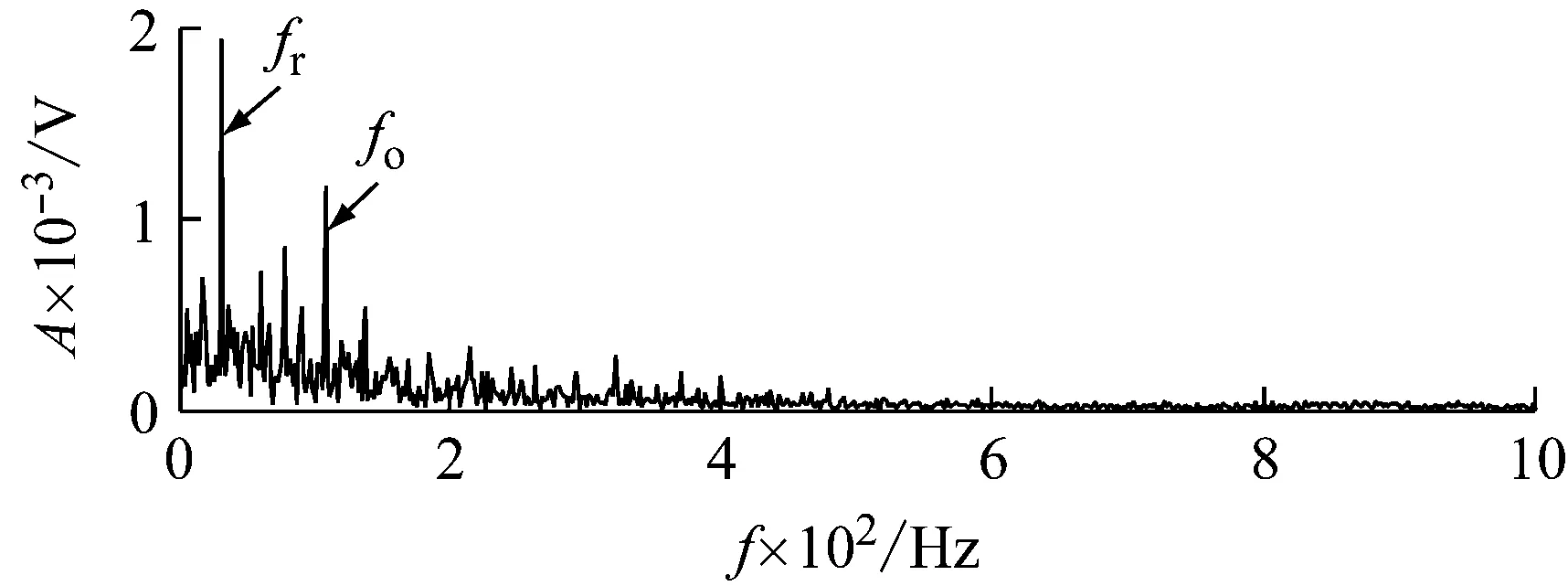
图11 本文方法故障分析结果
同样地,为了验证本文所提方法的优势,利用EMD对外圈故障数据进行处理。经分解后,得到11个IMF分量,计算各IMF的信息熵值,选取熵值最小的进行包络解调分析。经计算可知,IMF2的熵值最小,故选取IMF2进行包络解调分析,其包络谱,如图12所示。由图12可知,只能提取到外圈转频,无法提取外圈故障特征频率。显然,图11的效果明显优于图12。
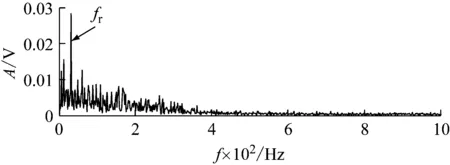
图12 外圈故障信号的EMD分解
4.2 内圈故障分析
为了证明本文方法的适用性,在这里对来源于美国西储大学的内圈故障数据进行了分析。型号及采样频率同“4.1”。故障尺寸为0.021″,转速为1 730 r/min,负载为2.205 kW,同样取8 000个数据点进行分析,由于原采集信号含噪量小,为了增加对比性且不失一般性,在其中加入了信噪比为-1 dB的高斯白噪声。经计算,其转频为fr=28.83 Hz,故障特征频率为fi=155.7 Hz。
如图13(a)、图13(b)所示为原信号的时域波形和包络谱。时域波形由于噪声影响,无法提取冲击特征;包络谱虽然可以提取转频和故障特征频率,但受到噪声严重包围。故对其进行预处理,提高信噪比。
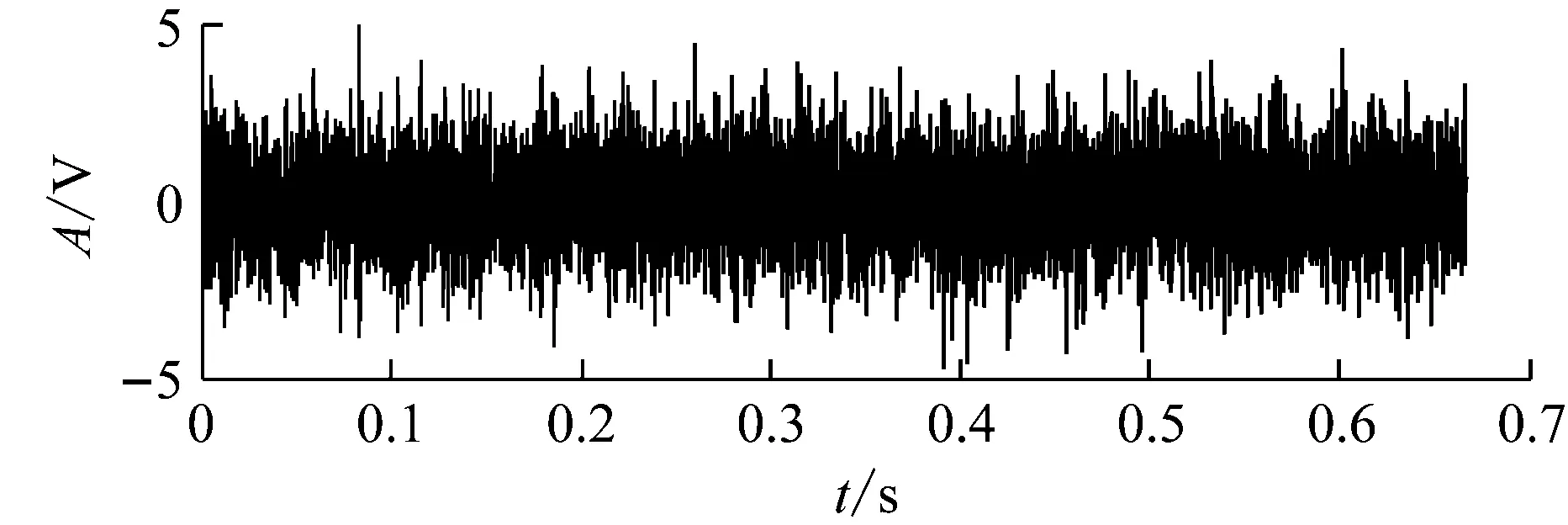
(a) 内圈故障时域波形
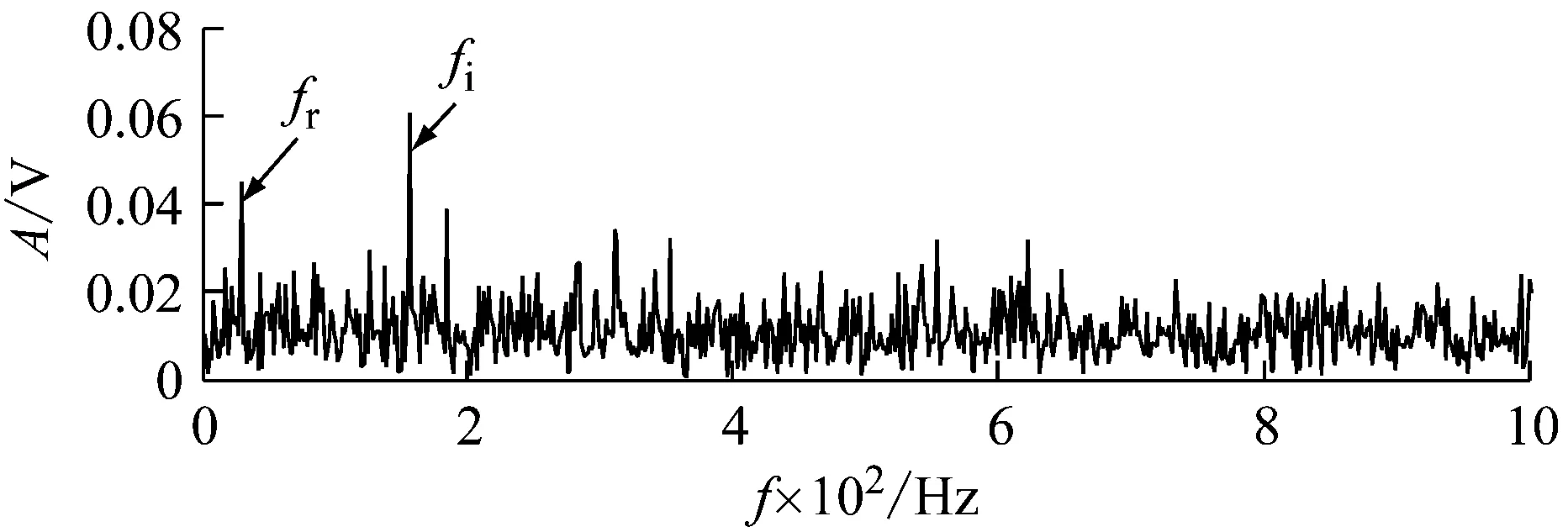
(b) 外圈故障包络谱
4.2.1 VMD参数优化
经过分析可得到当K=9时,取得熵最小值为0.627 0,所以取最优模态数为K=9。
同样地,在最优模态的基础上优化惩罚因子α。经分析可知,当α=1 000时,具有熵最小值0.602 5。由此,可得最优参数组合为[9,1 000]。
4.2.2 VMD分析及IMF选取
对信号进行VMD分解,获得9个IMF分量,根据“4.2.1”的优化过程,选取IMF5为敏感IMF分量,并对其进行包络解调分析。其包络谱,如图14所示。由包络谱可以清晰地提取出滚动体故障的故障特征频率fi及其转频fr,由此便可以判定轴承内圈故障。
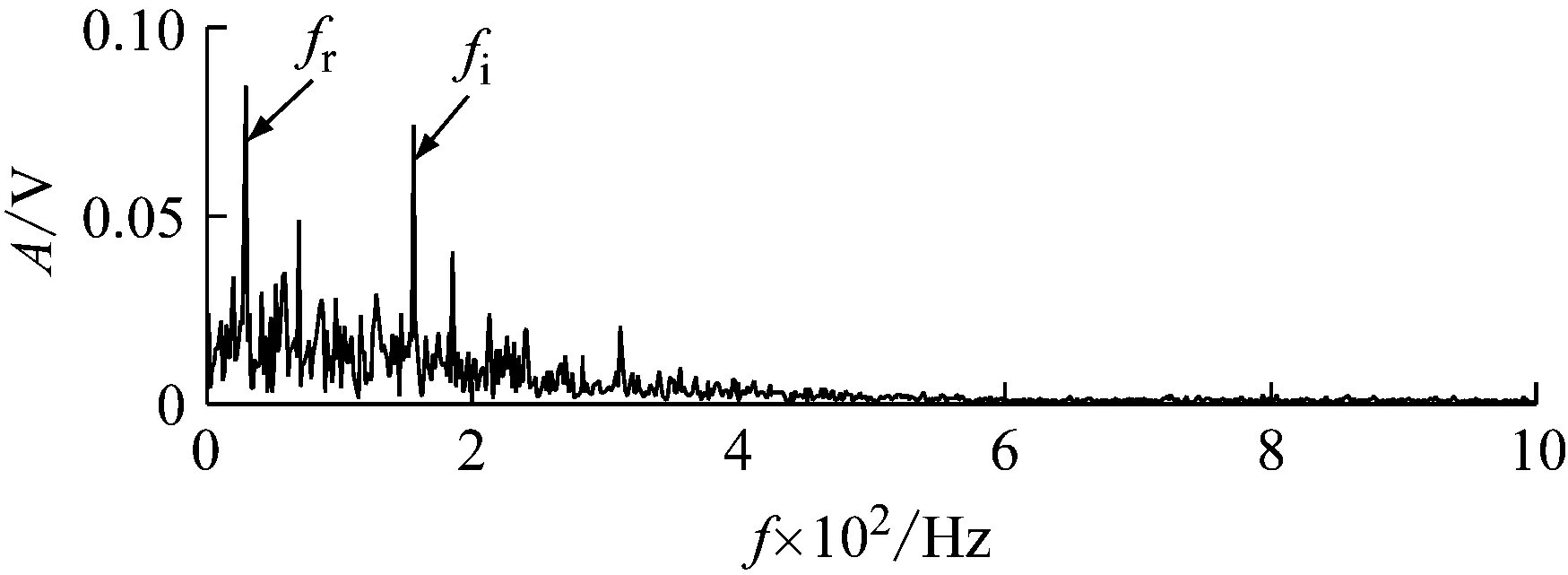
图14 本文方法故障分析结果
同样地,利用EMD对加噪内圈故障数据进行处理。经分解后,得到13个IMF分量,计算各IMF的信息熵值,选取熵值最小的进行包络解调分析。经计算可知,IMF2的信息熵值最小,故选取IMF2进行包络解调分析,其包络谱,如图15所示。由图15可知,内圈故障特征频率及其转频均无法从包络谱中提取出来。显然,图14的效果明显优于图15。因此,本文所提的方法显然具有优越性。
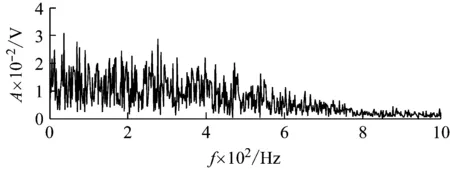
图15 内圈故障信号的EMD分解
5 结 论
(1) 滚动轴承早期故障特征通常比较信息微弱,提取较为困难,利用信息熵优化的变分模态分解方法能够有效地去除噪声,提取出微弱的故障特征信息。
(2) 针对变分模态分解多个IMF分量,需选取包含丰富故障特征信息的有效IMF的问题,利用信息熵最小值的有效IMF选取方法成功应用于仿真信号和实际数据,并取得良好效果。
(3) VMD克服了EMD的模态混叠等缺陷,是一种有效地自适应信号处理新方法。但其影响参数需要事先设定,对其影响参数的搜索范围的确定尚无理论依据。因此,需要进一步的深入研究。
