小间距比下串列双圆柱涡激振动数值模拟研究：振动响应和流体力

陈威霖， 及春宁， 许 栋

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

圆柱涡激振动是流固耦合的经典问题，近几十年对该现象的研究取得了大量的成果[1-3]。此外，涡激振动也常见于海洋、航空航天以及核能等众多的工程领域，比如输油立管、冷却管等，对该现象研究具有非常重要的实际意义。影响涡激振动的众多因素中，雷诺数和质量比是最受关注的。在低雷诺数(～O(102))时，圆柱的响应呈现出初始和下端两个分支[4-5],其中最大振幅出现在下端分支上；此时，质量比和阻尼不再是影响圆柱响应的主要因素。当雷诺数较高(≥O(103))时，质量-阻尼系数成为衡量圆柱响应的一个重要因素[6-7]：当质量-阻尼系数较低时，响应呈现出三个分支，分别为初始、上端和下端分支，其中最大振幅出现在上端分支上；当质量-阻尼系数较高时，响应则仅为两个分支，分别为初始和下端分支，其中最大振幅出现在初始分支上。

当圆柱的数量不再限定为一个，圆柱与圆柱、圆柱与流体之间的耦合作用变得更加复杂[8-9]。串列布置为众多情形中比较常见的一种，圆柱之间的相对位置决定了下游圆柱始终要受到上游圆柱脱落旋涡的影响，而下游圆柱对上游圆柱的影响则只存在于一定的间距范围内[10]。Prasanth等[11]对低雷诺数Re=100和大间距比L*=L/D=5.5(其中L为两圆柱中心的距离)下串列双圆柱涡激振动进行了数值模拟研究，发现下游圆柱响应要明显大于对应的单圆柱涡激振动，但类似于高雷诺数下单圆柱涡激振动的情况。受到上游圆柱的影响，下游圆柱的锁定区间要明显大于单圆柱涡激振动情况；此外，研究还发现大振幅的涡激振动不仅出现在锁定区域，在非锁定区间，响应振幅也可以很大。Zhao等[12]对直径比为0.5的串列双圆柱涡激振动在间距比L*=1.5～3.0范围内展开了研究，其中雷诺数为Re=200。研究发现，当间距比为1.5～2.0时，圆柱响应出现四个不同的分区。Bao等[13]应用基于有限元的数值方法研究了不同频率比下串列双圆柱涡激振动的情况，其中间距比L*=5.0和Re=150。研究表明，此时下游圆柱对上游圆柱的影响几乎可以忽略，而上游圆柱对下游圆柱则有显著的影响。此外，下游圆柱的流向响应对频率比的敏感程度要明显高于横向的情况。Mysa等[14]研究了串列双圆柱涡激振动中对响应起关键作用的因素，其中间距比L*=4.0～10.0和雷诺数Re=100。研究发现，上游圆柱的尾流与下游圆柱发生相互作用，其中与圆柱运动同相的成分对下游圆柱的振动起到了促进作用。King等[15]通过水槽实验研究了Re=103～2×104下串列双圆柱涡激振动的情况，其中间距比为L*=1.25～7.0。 结果显示，当间距比为6.5时，上游圆柱的响应与对应雷诺数下的单圆柱涡激振动相似。受上游圆柱的影响，下游圆柱的大振幅响应一直保持到实验的最大折合流速。Brika等[16]对雷诺数Re=5×103～2.7×104下串列双圆柱涡激振动进行了一系列的研究，其中间距比为L*=7～25。随着间距比的增加，上游圆柱的响应越来越接近单圆柱涡激振动的情况；即使在间距比L*=16～25下，上游圆柱对下游圆柱的影响仍然存在。Assi等[17]通过水槽实验研究了上游圆柱固定情况下的串列双圆柱涡激振动情况，相应的雷诺数为Re=3×103～1.3×104，间距比为L*=2.0～5.6. 在间距比L*=3.0～5.6时，下游圆柱的振幅随着折合流速增加而持续增加，出现了尾流弛振现象。此后，Assi等[18]对该尾流弛振现象通过一系列的实验进行更深入的研究，发现尾流弛振来源于下游圆柱与上游圆柱尾流之间的不稳定的旋涡-结构之间的耦合作用。

目前对串列双圆柱涡激振动的研究已经取得了相当多的成果，但是对小间距比(L*=1.1～1.5)下该现象的研究仍较少。且本文模拟结果显示，在小间距比下，圆柱之间存在较强的耦合作用，而且发现了一些新的现象，比如低雷诺数下串列双圆柱的尾流弛振现象等。

1 数值方法

1.1 控制方程

流体运动的数值模拟采用浸入边界法[19]，无量纲的控制方程如下

(1)

(2)

对以上控制方程采用二阶精度的Adams-Bashforth时间格式进行离散，可得控制方程的守恒形式如下

(3)

(4)

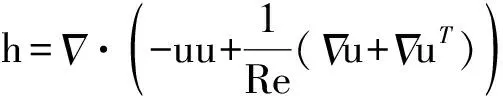
针对传统浸入边界法施加边界条件精度不高的情况，Ji等[19]提出了基于嵌入式迭代的浸入边界法，将浸入边界法嵌入到压强泊松方程的迭代求解中，利用压强的中间解比初始值更接近真实值的特点，迭代修正附加体积力，在不显著增加计算耗时的前提下，提高整个算法的求解精度。

对仅做横流向运动的刚性圆柱体，其无量纲运动方程可以用下述方程来描述

(5)

式中:y为无量纲位移;t为无量纲时间;m*为圆柱体质量比;FN=fnD/U∞为无量纲固有频率(fn为固有频率);ζ为结构阻尼比;Cl为圆柱受到的横流向流体力系数。方程采用标准的Newmark-β法求解。

以上流体和刚体运动控制方程采用圆柱直径D、来流速度U∞和流体密度ρ进行无量纲化。

1.2 问题描述

拟对小间距比下串列双圆柱涡激振动展开深入研究，数值模拟相关参数设置如下：两圆柱的间距比L*=L/D=1.1～1.5，Re=U∞D/υ=100(其中υ为运动黏性系数);折合流速Ur=U∞/fnD=3～30(最小间隔为ΔUr=0.5);质量比m*=4m/ρπD2=2.0(其中m圆柱的质量)。

为消除边界对圆柱涡激振动的影响，本文采用了较大的计算域,如图1所示。将计算域的坐标原点设在串列两圆柱距离的中心上，距离入口和出口边界为100D，距离上和下边界为50D。因此，相应的阻流比为B=D/H=0.01。Sen等[20]对圆柱绕流数值模拟研究发现，当阻流比B≤0.01时，阻流比对流动特征参数的影响不再重要。

图1 计算域与边界条件

采用正交笛卡尔网格对计算区域划分，X(流向)和Y(横向)方向的网格数分别为1 024和512，其中加密区域内无量纲网格尺寸Δx/D=Δy/D=1/64。加密区域为6.5D×4.0D;编号1和2分别为上游和下游圆柱。

计算域边界条件设置如下。入口边界为Dirichlet型边界条件(u=U∞,ν=0)；出口边界为Neumann型边界条件(∂u/∂x=0,∂v/∂x=0)；上下边界为自由滑移边界条件。

为了满足Courant-Friedrichs-Lewy条件，CFL数满足CFL=UmaxΔt/Δx≤0.5，其中，Umax为最大流速，Δt为时间步长,取为Δt=0.006。

2 方法验证

本文采用的数值模型和程序已从单圆柱绕流[21-22]，单圆柱涡激振动以及串列并列双圆柱[23-25]等多角度进行了验证，读者可自行查阅。

3 结果和讨论

3.1 振动响应

当间距比为L*=1.1，两圆柱的响应从折合流速Ur=3.0开始增加，当折合流速Ur>4.0以后，圆柱的响应开始急剧增加，并在折合流速Ur=9.0时两圆柱响应同时达到最大值，分别为Yrms/D=0.39和Yrms/D=0.58。上游圆柱的最大响应与单圆柱涡激振动的最大振幅[27]Yrms/D=0.40非常接近，而下游圆柱则要明显大于单圆柱涡激振动的情况。但是，相比于较大间距比下的串列双圆柱涡激振动[28-29]，如图2(a)所示，两圆柱的响应则小了一些。两圆柱的响应均在Ur=9.0以后发生下降，上游圆柱分别在折合流速Ur=12.0和Ur=14.0时经历一个谷值和一个峰值，其大小为Yrms/D=0.27和Yrms/D=0.39；下游圆柱同样经历了一个谷值(Ur=12.0)和一个峰值(Ur=20.0)，其大小为Yrms/D=0.35和Yrms/D=0.60。此后，下游圆柱的响应随折合流速急剧下降，而上游圆柱则经历了一个比较平缓的区域(Ur=17.0～22.0)才急剧下降。

从圆柱响应随折合流速变化的情况可知，此时圆柱响应不再与单圆柱涡激振动相似，没有出现初始和下端分支[30]，而且圆柱的大振幅响应出现在更大的折合流速范围内(Ur=4.0～28.0)，远大于单圆柱涡激振动的范围(Ur=4.0～8.5)。这些不同反映了串列双圆柱涡激振动在小间距比下强烈的耦合作用，而该耦合机制将在下部分进行详细的分析。

需要说明的是在折合流速从Ur=3.5～4.0的过程中出现了一个突然的下降，这是圆柱与流体之间相互作用的结果，此现象的机制已在文献[27]中提及。

当间距比为L*=1.2时，以折合流速Ur=4.0和Ur=15.0为界，串列双圆柱的响应呈现出三个分支。圆柱响应在Ur=3.0～4.0时缓慢增加直到Ur>4.0以后响应突然增加，圆柱响应振幅分别在折合流速Ur=14.0和Ur=12.0时取得最大值Yrms/D=0.44和Yrms/D=0.63，该最大值要稍大于间距比L*=1.1的情况。在折合流速Ur>15.0以后，两圆柱的振幅出现急剧下降，并均在折合流速Ur=20.0时达到一个谷值(Yrms/D=0.29)；此后，下游圆柱响应随着折合流速而持续增加，而上游圆柱则要经历一个平稳区域(Ur=20.0～28.0)，之后圆柱响应随折合流速增加。在大折合流速下，圆柱响应随折合流速增加的情况类似于高雷诺数下串列双圆柱涡激振动的尾流弛振现象[31-33]，为首次出现在低雷诺数串列双圆柱涡激振动中；说明了该间距比下圆柱与流体之间的耦合作用与此前不再相同，其耦合机制将在下部分详细阐述。

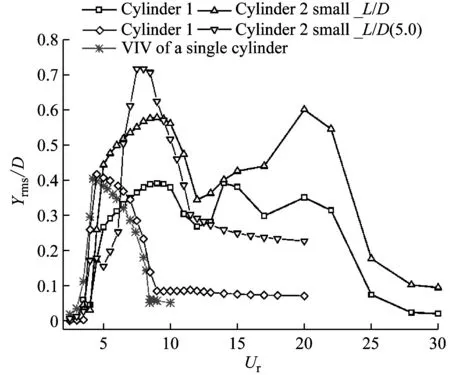
(a) L/D=1.1

(b) L/D=1.2

(c) L/D=1.3

(d) L/D=1.5

当间距比为L*=1.3时，串列双圆柱的响应均呈现出四个分支。第一分支出现在Ur=3.0～4.0范围内，此时圆柱响应稍大于零且不随折合流速变化；当折合流速Ur>4.0以后，圆柱响应进入第二分支，此时振幅急剧增加，一直到Ur=8.5以后，圆柱响应出现另一个更急剧的上升(第三分支)，两圆柱响应最大值Yrms/D=0.46和Yrms/D=0.74同时在Ur=9.0时取得。该最大值要稍大于更小间距比L*=1.1～1.2的情况。在折合流速Ur=9.0～23.0内，上游圆柱响应几乎保持不变而下游圆柱响应随折合流速缓慢下降。之后，两圆柱响应均急剧下降，在折合流速Ur=24.0时达到谷值(Yrms/D=0.17)；圆柱响应此后随折合流速增加而持续增加(第四分支)。需说明的是此时下游圆柱的响应要明显小于上游圆柱的情况，该现象仅在此间距比下出现，此时圆柱与流体之间的耦合作用也与其余情况不同。

当间距比为L*=1.5时，圆柱响应与间距比L*=1.3的情况相同在折合流速Ur=3.0～4.0内在零附近且保持不变；之后圆柱响应随折合流速快速增加，上游圆柱在折合流速Ur=6.5时取得最大值Yrms/D=0.54，下游圆柱的最大值Yrms/D=0.77则在Ur=7.5时得到。之后，圆柱响应随折合流速增加而缓慢减小，在折合流速Ur≥28.0之后，圆柱响应不再变化。在模拟的最大折合流速Ur=30.0下，两圆柱的响应振幅分别为Yrms/D=0.35和Yrms/D=0.55，均要远大于单圆柱涡激振动的情况，而且此时下游圆柱的振幅甚至要比单圆柱涡激振动的最大振幅(Yrms/D=0.40)大37.5%。

需要说明的是上游圆柱响应在Ur=4.5～5.0之间出现了类似间距比L*=1.1时的突然下降情况，但与之不同的是此时下游圆柱的响应并未出现下降，该现象的原因分析如下。如图3所示，当折合流速Ur=4.5时，上游圆柱和下游圆柱位移的相位差维持在φy=101°上；当折合流速Ur=5.0时，上游圆柱和下游圆柱位移的相位差维持在φy=77.5°上。对于前者，当上游圆柱位于平衡位置时，下游圆柱恰好位于向最大负位移运动的过程中，此时上游圆柱后有充足的空间使得旋涡向下游移动，因此，为上游圆柱的运动提供了足够的动力；对于后者，当上游圆柱位于平衡位置时，下游圆柱恰好位于由最大负位移向平衡位置运动的过程中，下游圆柱的运动使得上游圆柱后的旋涡自由脱落的空间越来越小，因此，在一定程度上阻碍了上游圆柱的振动，使得其振幅下降。

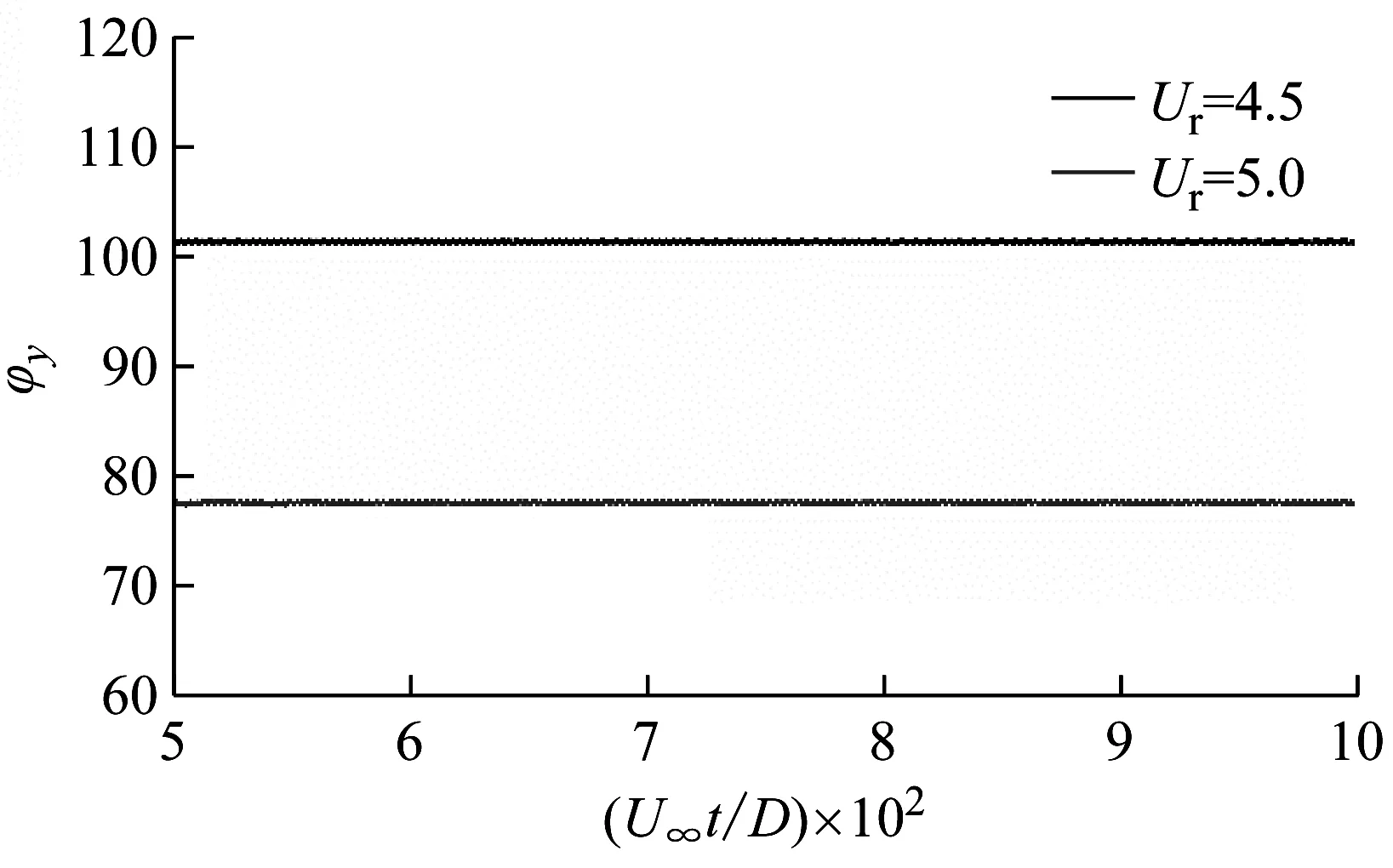
图3 折合流速Ur=4.5和Ur=5.0下串列双圆柱位移相位差

Fig.3 Phase difference between the displacements of two tandem cylinders atUr=4.5 andUr=5.0

总结起来，如图2所示，小间距比下串列双圆柱涡激振动与大间距比(L*=5.0)下完全不同；此时串列双圆柱的锁定区间要明显大于大间距比下的情况。在折合流速较小时(Ur≈10～15)，小间距比下串列双圆柱的响应呈现出随折合流速增加而增加；当折合流速较大时，各间距比下串列双圆柱的响应则明显不同。当L*=1.1时，串列双圆柱的响应呈现出先增加再急剧下降到接近于零，而L*=1.2时，两圆柱的响应随折合流速增加而增加，并未出现下降。与前两个间距比不同的是间距比L*=1.3的不规律振动出现在更大的折合流速下，响应随折合流速的增加而增加，未出现下降。当L*=1.5时，串列双圆柱的响应在大折合流速以后随着折合流速缓慢下降。

3.2 流体力系数

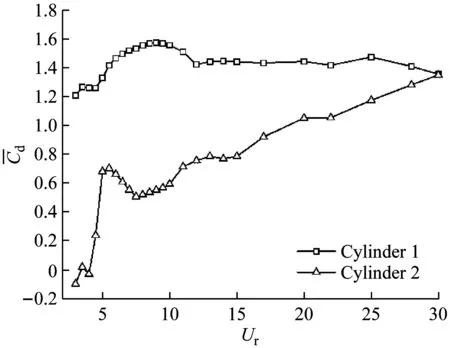
(a) L/D=1.1

(b) L/D=1.2

(c) L/D=1.3

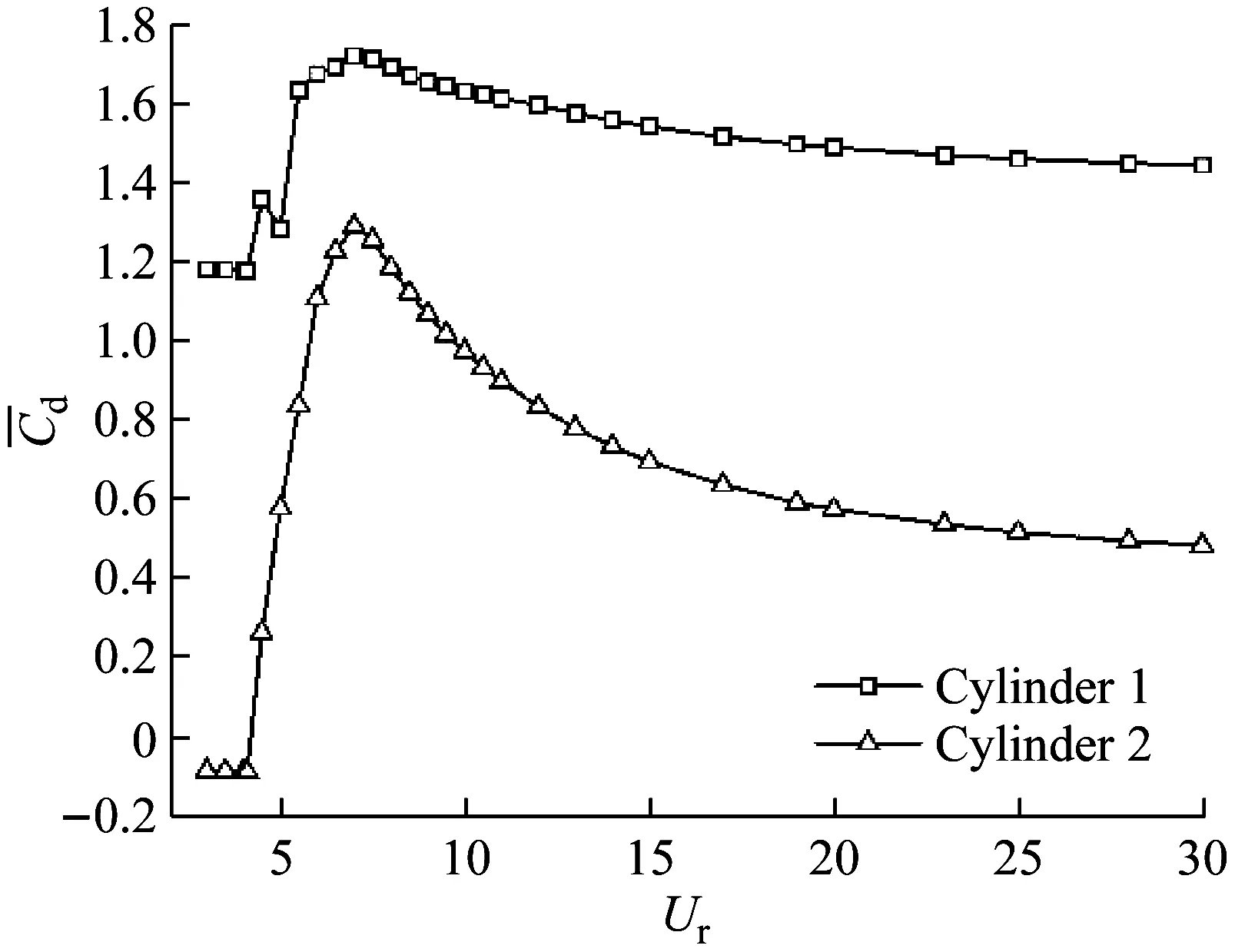
(d) L/D=1.5

Fig.4 The mean drag coefficients versus the reduced velocity at different spacing ratios

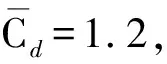
(a) L/D=1.1

(b) L/D=1.2

(c) L/D=1.3

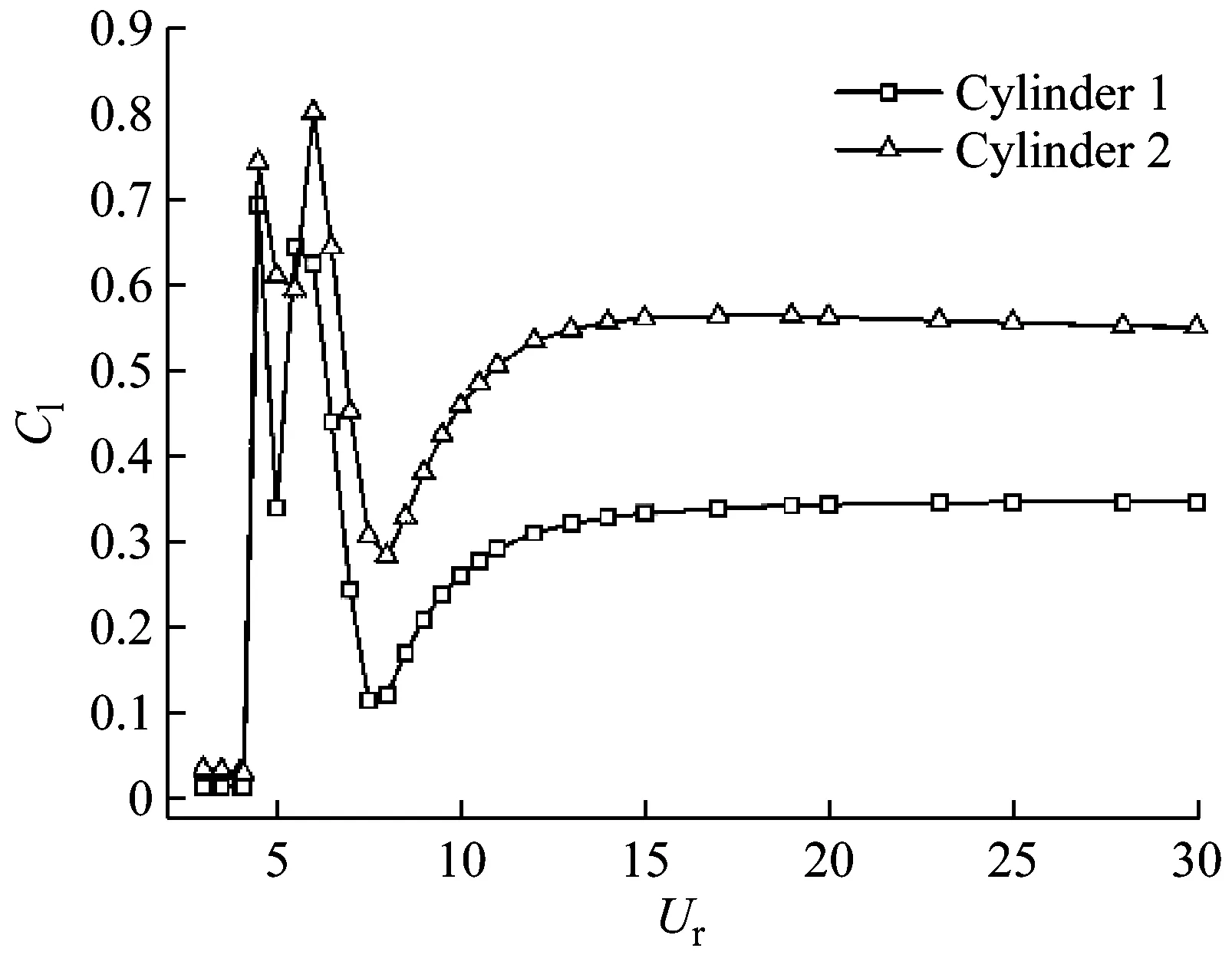
(d) L/D=1.5

Fig.5 The RMS lift coefficients versus the reduced velocity at different spacing ratios

如图5所示，各间距比下，串列双圆柱的升力均方根随折合流速呈现出不规律的变化。当间距比L*=1.1时，上游和下游圆柱的升力均方根呈现出相似的变化。上游圆柱呈现出四个先增后减的趋势，折合流速Ur=3.5、Ur=4.5、Ur=6.5、Ur=15.0时分别对应相应的峰值，而折合流速Ur=4.0、Ur=6.0、Ur=7.0时分别对应相应的谷值。上游圆柱的升力均方根在Ur≥15.0以后，迅速下降并在Ur≥28.0以后稳定下来。下游圆柱的升力均方根呈现出三个先增后减的趋势，折合流速Ur=3.5、Ur=4.5、Ur=10.0时分别对应相应峰值，而折合流速Ur=4.0、Ur=7.0时分别对应相应谷值。此后下游圆柱的升力均方根随折合流速下降，但在折合流速Ur≥22.0以后，升力均方根随折合流速缓慢增加。

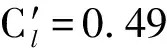
当间距比L*=1.3时，两圆柱的升力均方根趋势与间距比L*=1.2时的情况几乎一致，仅在折合流速Ur≥24.0以后不再相同。在折合流速Ur=24.0～30.0内，两圆柱的升力均方根均较小，且随折合流速仅稍微增加。需要说明的是，虽然此区域内上游圆柱的响应要大于下游圆柱，但上游圆柱的升力均方根却要小于下游圆柱的。

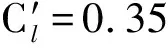
值得注意的是在串列双圆柱涡激振动中，两圆柱的升力均方根均在折合流速Ur=7.0～8.0范围内出现一个谷值，而且在间距比L*≤1.3时，两圆柱的升力均方根值甚至要小于振幅几乎为零的折合流速Ur=3.0时的情况。出现这种现象的原因是该谷值对应的折合流速下，两圆柱的升力不再由单一频率成分组成，其中上游圆柱的高倍频占主导而下游圆柱的基频占主导。以间距比L*=1.2为例，对两圆柱升力(Ur=7.0)的小波分析表明，如图6(a)所示，上游圆柱的升力主频为3倍频(f=0.429)；而下游圆柱的主频为基频(f=0.143)，如图6(b)所示。此外，提取与两圆柱运动同相的升力成分发现，此时与两圆柱运动同相的升力成分较大；这说明高频成分的存在提高了与两圆柱运动同相的升力成分，因此保证了圆柱能以较大的振幅振动。

(a) 上游圆柱

(b) 下游圆柱

图6 对应间距比L*=1.2和折合流速Ur=7.0时上游和下游圆柱的升力和频域的历时曲线

Fig.6 Time history of the lift coefficient and the frequency of upstream and downstream cylinder atL*=1.2 andUr=7.0

在圆柱涡激振动中，通过快速傅里叶变换(FFT)对圆柱的升力脉动值进行分析得到其主导频率并将其定义为St数。当间距比L*≤1.3时，由于圆柱之间的耦合作用较强，使得某些折合流速下圆柱升力的频谱混乱，无法得到相应的St数，比如L*=1.1的Ur=12.0～25.0；因此，本文仅考虑间距比L*=1.5时的情况。如图7所示，两圆柱的St数在绝大多数折合流速下是相等的。当折合流速Ur=5.5时，两圆柱的St数不再相等，且两频率不是倍数关系；这反映出两圆柱之间的耦合作用无法实现稳定。该折合流速下，两圆柱的响应恰好处在由小振幅向大振幅的过渡，因此，可以看作是一个调制的阶段。

图7 间距比L*=1.5时St数随折合流速变化情况

另外，在折合流速Ur=7.5～8.5范围内，上游和下游圆柱的主导频率为基频的三倍，而该现象的出现与圆柱升力与位移相位差的跳跃有关。

4 结 论

本文对小间距比下串列双圆柱涡激振动进行了广参数空间的数值模拟研究，其中Re=100，间距比为L*=1.1～1.5，折合流速为Ur=3.0～30.0。为保持两圆柱间距不变，两圆柱仅作横向振动。对圆柱响应的研究发现，在小间距比下，圆柱的响应呈现出完全不同于大间距比下的情况；上游圆柱的响应也与单圆柱涡激振动有很大区别，没有初始和下端分支。根据响应的不同，可以分为三种。当间距比L*≤1.1时，响应存在于较大的折合流速范围内(Ur=4.0～28.0)，且在大折合流速内，两圆柱之间的耦合作用不再稳定。当间距比L*=1.2～1.3时，响应在小折合流速时呈现出类似于单圆柱涡激振动的现象，而类似高雷诺数串列双圆柱中的尾流弛振现象出现在大折合流速下，且随间距比的增加，开始该现象的折合流速增大。当间距比L*≥1.5时，响应随折合流速增加到最大值以后缓慢减小，并最终稳定在某个值上。

在小间距比下，串列双圆柱涡激振动的响应幅值相比于大间距比下要小一些。上游和下游圆柱的最大响应均随间距比增加而增加；当间距比L*=1.5时，下游圆柱的最大振幅达到了Yrms/D=0.77，且随间距比的进一步增加而下游圆柱的最大振幅减小，说明上游和下游圆柱之间的耦合作用在间距比L*=1.5时达到最大。

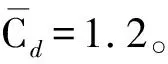
串列双圆柱的脱涡频率(St数)反映的是圆柱之间耦合作用的结果。当间距比L*=1.5时，在某些折合流速(Ur=5.5)下，上游和下游圆柱的脱涡频率不再相等，此时圆柱之间的耦合作用不再稳定。此外，在某些折合流速下，三倍基频占主导。