扁平管膨胀性能仿真及实验研究

冯丽娜, 李 东, 田建东, 孙 璟, 吴晗玲, 陈 荣

(1. 北京宇航系统工程研究所， 北京 100076； 2. 中国运载火箭技术研究院， 北京 100076；3. 国防科技大学 文理学院， 长沙 410073)

膨胀管分离装置作为一种典型的清洁线式分离装置，在航天运载器上得到了广泛的应用。早在约上世纪六十年代初期左右，美国洛克希德公司(Lockheed Missiles & Space Company)在柔性导爆索分离技术的基础上首先提出了膨胀管分离装置的概念，并进行了初步的研制，利用扁平的钢管，把炸药索嵌在钢管的中心，钢管的剩余空间用硅橡胶填满。试验结果表明该种分离装置非常有效，炸药的爆轰产物使扁平的钢管变成圆形，从而切断蒙皮，但没有任何污染物和碎片溢出，分离冲击也得到了有效的降低。1968年洛克希德公司Blain以“爆炸作动器”注册专利(US Patant No.3373686)[1]。后续在该结构基础上产生膨胀管-凹槽板分离装置(Super Zip，Sure-Sep等)，膨胀管-凹口螺栓分离装置，冗余膨胀管-凹槽板分离装置以及非断裂破坏的膨胀管分离装置等结构形式[2-8]。这些装置都是以扁平管组件(扁平管，填充物，炸药索)作为动力源头，在断裂部件或断裂方式上进行改进。其中，典型的膨胀管凹槽板分离装置的构型如图1所示[9]。

膨胀管分离装置作用时，不是将导爆索的爆炸能量直接作用于分离连接件上，而是通过填充物和扁平管的膨胀变形撑断分离板达到解锁分离的目的。整个作用系统受力均匀，受冲击载荷低，且爆炸产物始终密封于金属管内，既具有线式分离装置的优点，又达到了低冲击、无污染的目的。因此，该分离装置受到了各国航天界的重视，开展了大量的研究工作，并在多个型号上获得应用，如美国载人飞船轨道试验站的防护罩分离装置、阿金纳火箭的级间分离、“三叉戟”导弹第三级发动机分离装置、航天飞机和先进的航空飞机救生舱的分离、日本H-Ⅰ、H-Ⅱ运载火箭的卫星整流罩分离等[10-11]。我国对膨胀管分离装置的研究起步较晚，但经过十几年的自主研制，获得了大量的成果[12-17]，积累了一定的经验。

图1 典型的膨胀管分离装置

Fig.1 Typical expanding tube separation device

由于爆炸分离过程是一个高度非线性瞬态动力过程，涉及几何非线性、物理非线性以及接触非线性等多重非线性[17-19]，无论是国外可查阅的文献还是国内已知的一些研究报告，很多是关于试验研究的规律总结[20-21]。近年来，也有部分文献使用有限元进行仿真分析[22]，但缺乏膨胀管分离装置各部件详细参数对其膨胀性能影响的深入分析。

在膨胀管分离装置中，扁平管组件是分离装置的能量源，对其进行细致的分析有利于结构的优化和改进。本文使用LS-DYNA对自由扁平管组件进行仿真分析，通过实验验证有限元分析的准确性，并进一步通过有限元仿真研究扁平管壁厚、填充物密度以及弹性模量对其膨胀性能的影响。

1 有限元仿真分析及实验验证

1.1 有限元模型

1.1.1 有限元模型建立

建立扁平管组件的几何模型并划分有限元网格，如图2所示。其中，扁平管设置为Lagrange网格，炸药、填充物和空气为Euler网格。为尽可能减少计算量，并保证Lagrange网格在Euler网格区域内变形运动，设置空气模型的形状如图2所示，将扁平管的横向设置为x轴，纵向设置为y轴。

1.1.2 材料模型

本节所采用的材料模型参数取自参考文献[13-15]及相关研究报告。各部件的相关模型及参数，如表1所示。

(a) 几何模型

(b) 有限元模型

部件材料具体参数炸药索黑索金ρ=1.5 g/cm3; D=7 000 m/s; PCJ=23.11 GPa填充物高分子聚合物ρ=0.95 g/cm3; E=3 GPa; v=0.47;σy=0.015 GPa扁平管1Cr18Ni9Tiρ=7.83 g/cm3;E=205 GPa;v =0.29; σy =0.34 GPa;k=1.34 GPa;n=0.34空气空气ρ=1.29×10-3 g/cm3

表1中：ρ为材料密度；D为炸药爆速；PCJ为CJ压力；E为弹性模量；ν为泊松比；σy为屈服应力；k，n为材料的硬化系数。

扁平管在有限元分析中所使用的材料模型为MAT_POWER_LAW_PLASTICITY。该模型提供了各向同性硬化的弹塑性模型。屈服应力σy为塑性应变的函数，满足式(1)，表1中的σy值为材料的初始屈服应力[23]

(1)

炸药和空气需使用相应的状态方程。炸药的状态方程为JWL状态方程。具体形式为

(2)

具体参数如表2所示，其中，V0为初始相对体积。

空气材料的状态方程选用线性多项式，方程形式为

表2 炸药的状态方程参数

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(3)

其中，μ=ρ/ρ0-1，对于气体，使用γ准则方程。设置C0=C1=C2=C3=C6=0，C4=C5=γ-1，其中γ是比热比例，压力可以表示为

(4)

其具体参数如表3所示。

表3 空气的状态方程参数

1.2 实验验证

使用全光纤激光多普勒测速仪(Displacement Interferometer System for Any Reflector, DISAR)对自由扁平管在膨胀过程中的上表面和侧面的速度进行测量，该仪器主要用于冲击波物理和爆轰物理研究中位移或速度的连续观测。其基本原理主要是利用光学多普勒效应实现对位移或速度的测量。该实验中炸药从扁平管的一端起爆，实验状态如图3所示。

图3 实验测速图示

1.3 仿真实验结果对比分析

有限元分析中将炸药索设置为从一端起爆，计算终止时间200 μs。选取有限元结果的输出点与实验所测位置相同，如图4所示。爆炸是一个极迅速的过程，起爆时间存在误差，为更好的比较实验和仿真结果，将实验和仿真中测点膨胀的起始点设为零点，获得扁平管窄处(上端面)速度仿真和实验结果如图5(a)所示，宽处(侧面)速度如图5(b)所示。其中，宽处的速度实际测量只采集到9 μs内的有效数据。由于测试仪器的端头与被测试件之间为平面粘接，在扁平管膨胀过程中，侧面与测试端头的接触面积迅速减小，端头随即与测试件分开，因此，测量到的有效数据有限。而对于上端面，在膨胀过程中，接触面积增加，测试端头与试件不易分开，因此得到的有效数据点较多。

图4 有限元结果输出点的位置

在数据处理中，统一将扁平管向外膨胀时的速度设为正值，向内收缩的速度设为负值。由于DISAR只能采集到速度的幅值，不能判断速度的方向。因此，在图5(a)中，将部分曲线对称到时间轴下方，如图中虚线所示，实验所测窄处的膨胀速度极值为103.50 m/s，有限元结果为126.11 m/s。实验测得宽处在9 μs内的膨胀速极值为228.52 m/s，有限元结果为238.49 m/s。实验和仿真得到的速度曲线变化趋势一致，数值上存在一定差异。分析误差原因，在实际实验中，扁平管的尺寸、炸药索的药量等与设计值存在一定的偏差，实验中填充物和扁平管之间会存在间隙，而仿真分析中二者紧密接触。此外，测量使用仪器设备也会有一定的误差。由此，在误差范围内认为该仿真分析可以预测自由扁平管在炸药索爆炸作用下的运动和变形特征。

(a) 窄处(上端面)速度仿真实验对比

(b) 宽处(侧面)速度仿真实验对比

从仿真和实验可以得出结论，扁平管横向膨胀速度远大于纵向膨胀速度，这由扁平管的几何尺寸决定。若将扁平管的窄处和宽处看做梁结构，宽处的跨距相对较大，可变形的空间较大，且宽处与炸药距离更近，受到的冲击更大。因此，爆炸冲击的变形更倾向于集中在宽处。

通过仿真分析，给出不同时刻扁平管的变形截面图，选取截面位置如图6(a)所示。几个不同时刻的变形截面如图6(b)所示。

(a) 截面位置

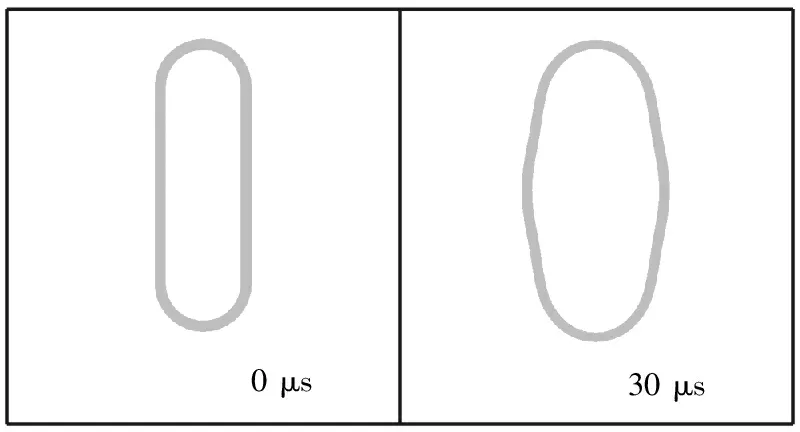
0 μs30 μs

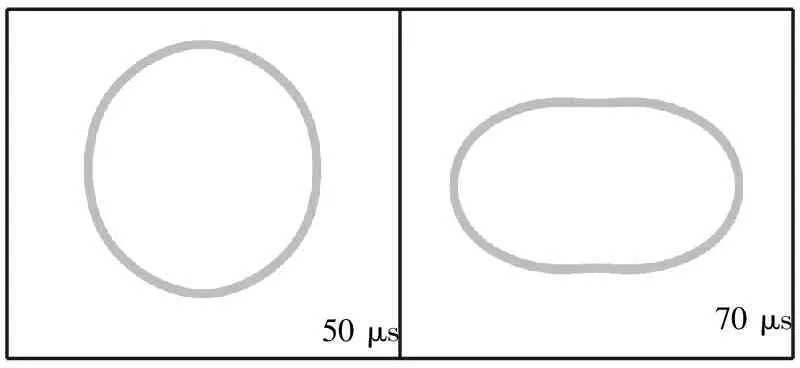
50 μs70 μs

100 μs140 μs

(b) 扁平管不同时刻变形图

图6 仿真结果中不同时刻扁平管变形截面图

Fig.6 Expanding tube deformation section at different times of simulation results

比较图6(b)中扁平管的变形图，其纵向膨胀位移很小，在稍向外膨胀后会大幅度向内回收，后又稍向外膨胀。而其横向膨胀位移很大，并且在横向膨胀位移达到极值后也会向内收缩。分析其原因，炸药索爆炸后以很大的能量推动扁平管，扁平管加速向外膨胀。当扁平管膨胀到一定大小时，由于变形产生的应力与爆炸产物对其的推力平衡，扁平管向外膨胀的加速度为零，速度达到膨胀速度极值，扁平管以该速度极值继续减速向外运动。当速度降为零时，其变形产生的应力大于爆炸产物的推力，向内收缩的加速度最大，则扁平管以该加速度向内运动。这样来回的运动，类似于“脉动”的过程，直至所有能量被消耗。

2 扁平管壁厚对膨胀速度的影响

本节利用仿真分析的方法研究了扁平管壁厚对其膨胀速度和膨胀位移的影响，选择扁平管的壁厚分别为0.8 mm、1.0 mm、1.2 mm和1.4 mm。有限元模型如图7所示。

图7 不同壁厚的扁平管有限元模型示意图

为保证其它条件相同，内部填充物以及炸药索的几何参数等都不变，向外扩展扁平管的壁厚。算法与第1节相同，计算终止时间为120 μs。选取扁平管外表面上的点1和点2输出其膨胀变形结果。点1的速度及位移-时间曲线如图8所示。改变扁平管壁厚时，其速度变化趋势相同，仅是速度幅值出现差异。扁平管壁厚越大，其速度及位移变化范围越小，膨胀速度、向内收缩的速度、向外膨胀的位移越小。由于随着壁厚的增加，扁平管刚性增加，可变形的空间减小，则速度和位移变化量都减小。扁平管点1的膨胀速度及位移极值如表4所示，壁厚为0.8 mm的扁平管点1的纵向膨胀速度和位移最大。

表4不同壁厚扁平管点1纵向膨胀速度及位移极值

Tab.4Extremelongitudinalexpandingvelocityanddisplacementatpoint1ofexpandingtubewithdifferentthickness

壁厚/mm0.81.01.21.4vymax/(m·s-1)126.11114.21102.5692.54dymax/mm0.480.440.390.35

输出点2的横向速度和位移曲线，如图9所示。横向膨胀速度及位移极值如表5所示。可以得到类似的结论，壁厚越大，速度极值越小，膨胀位移极值越小。对于壁厚为0.8 mm和1.0 mm两种情况，点2速度变化曲线有两个峰值，分析其原因，炸药爆炸后，填充物将爆炸产生的能量迅速传递给扁平管，点2处会产生大于填充物的速度向外膨胀，在该位置附近填充物与扁平管之间产生微小空隙，由于没有能量的供给，点2速度略有降低，而填充物在爆炸产物的驱动下继续膨胀，会再次给予其能量的补充，因此，产生第二个峰值。随着扁平管壁厚的增加，其质量、刚性增加，在相同能量作用下，其速度变化更加缓慢，对于1.2 mm和1.4 mm的扁平管，其点2的膨胀速度有三个峰值。壁厚为0.8 mm时，点2的横向膨胀速度及位移最大。对比表4、5，点2的速度极值以及位移极值都大于点1，与第1节中的结论相同。

(a) 纵向速度-时间曲线

(b) 纵向位移-时间曲线

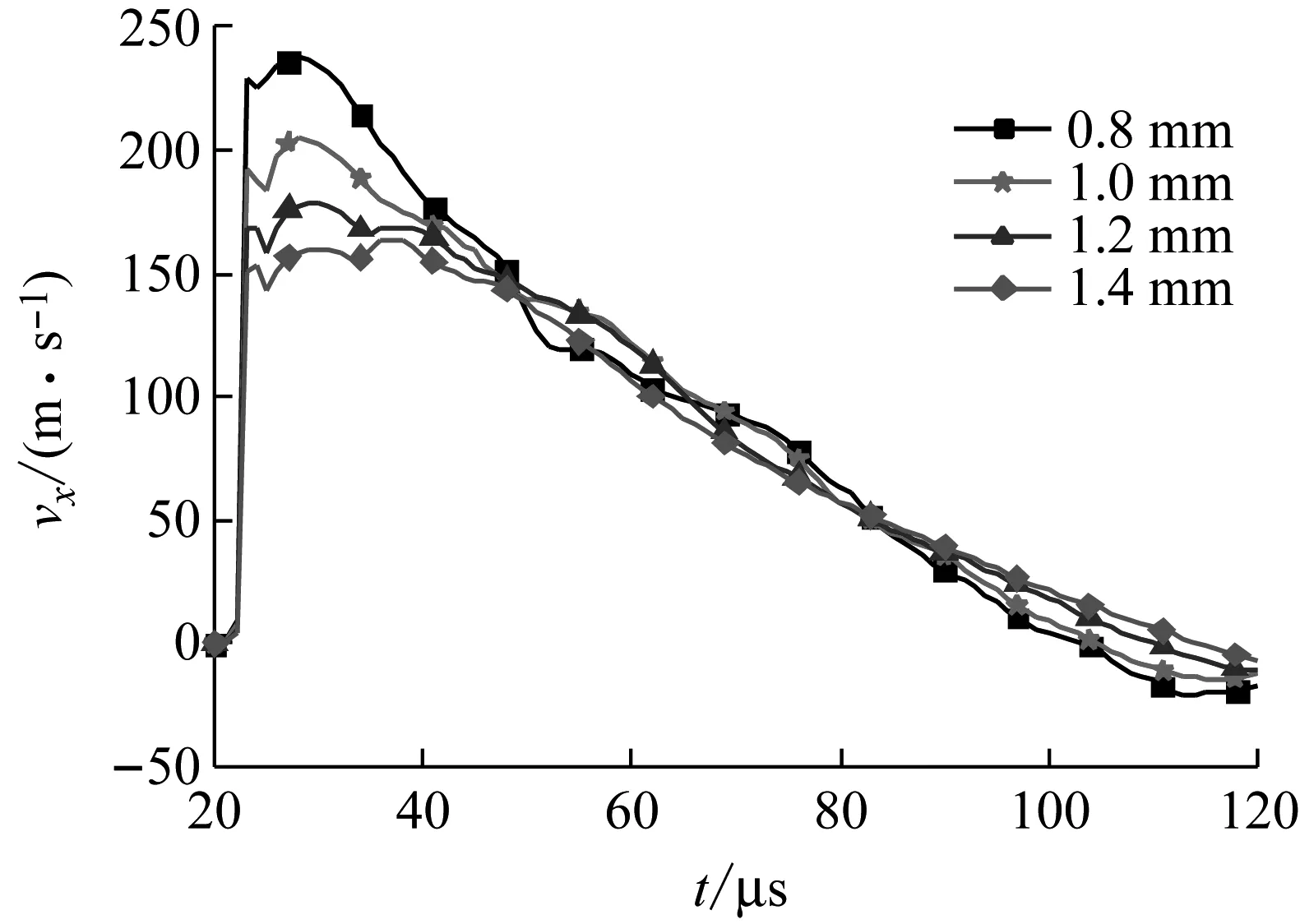
(a) 横向速度-时间曲线

(b) 横向位移-时间曲线

表5不同壁厚扁平管点2横向膨胀速度及位移极值

Tab.5Extremetransverseexpandingvelocityanddisplacementatpoint2ofexpandingtubewithdifferentthickness

壁厚/mm0.81.01.21.4vxmax(m·s-1)238.49204.52179.10163.94dxmax/mm9.098.768.407.98

为分析能量输出规律，绘制扁平管的动能变化曲线，如图10所示。动能极值如表6所示，动能随壁厚不是单调变化，壁厚为1.2 mm时，扁平管动能最大，能量输出更多。分析其原因，扁平管动能受其质量和速度两个因素影响，在一定范围内质量起关键因素，扁平管动能随壁厚增加而增加。当扁平管壁厚过大时，其刚性增强，不易变形，此时，速度起关键作用，动能又呈下降趋势。

图10 不同壁厚扁平管动能仿真结果

壁厚/mm0.81.01.21.4Ek/J738.61777.58787.27774.97

3 填充物密度及弹性模量对膨胀速度的影响

扁平管内填充物起到支撑炸药，将炸药能量传递给扁平管的作用，对结构性能有很大的影响。本节使用有限元分析的方法研究了不同密度及不同弹性模量的填充物对扁平管膨胀性能的影响。共计算7种情况。具体参数如表7所示。

其它参数不变，几何模型完全相同。计算结果显示填充物密度较大时，扁平管横向达到最大膨胀量所需要的时间较长，因此，将计算终止时间调整为190 μs。

表7 填充物的参数

输出填充物参数不同的情况下点1的纵向膨胀速度曲线和位移曲线，如图11所示，速度及位移极值如表8所示。其中编号为1，2，3，4的填充物弹性模量都为3 GPa，其它参数不变，仅密度不同。随着填充物密度的增大，点1向外膨胀的速度减小，后续向内回收的速度也减小，并且扁平管变形缓慢，其在纵向由膨胀转为收缩，再转为膨胀所需的时间都增加。曲线在时间轴上向右偏移，由于随着填充物密度的增加，其质量增加，惯性增强，变化趋于平缓。如表8所示，随填充物密度的增加，点1向外膨胀的速度极值减小。密度为0.5 g/cm3和0.95 g/cm3的两种情况下点1的膨胀位移极值基本相同，再继续增加填充物密度，其膨胀位移极值减小。编号为5，2，6，7的填充物密度均为0.95 g/cm3，仅弹性模量不同，与之对应的四条曲线的变化规律相似，仅幅值有所差异。随着填充物弹性模量的增加，扁平管点1向外膨胀的速度和位移都减小。由于填充物弹性模量增加时，其变形较难，导致作用于扁平管点1时，其膨胀速度和位移都减小。

(a) 纵向速度-时间曲线

(b) 纵向位移-时间曲线

Fig.11 Simulation velocity results at point 1 of expanding tube with different density and Young’s modulus of the filler material

表8填充物密度及弹性模量不同时扁平管点1膨胀速度及位移极值

Tab.8Extremelongitudinalexpandingvelocityanddisplacementatpoint1ofexpandingtubewithdifferentdensityandYoung’smodulusofthefillermaterial

编号1234ρ(g·cm-3)0.50.9559vymax/(m·s-1)127.09126.1165.0649.56dymax/mm0.470.480.210.18编号5267E/GPa13713vymax/(m·s-1)128.66126.1179.6646.49dymax/mm0.530.480.350.34

输出扁平管上点2的速度和位移曲线，如图12所示，点2 的速度及位移极值如表9所示。对比曲线1，2，3，4，当填充物密度较大时点2膨胀速度极值所对应的时间较短，说明在填充物密度较大时，可快速给扁平管横向一个较大的冲量，并且，由于填充物密度大惯性大，其反向收缩所需时间增加，反向收缩速度较小。对比速度极值，如表9所示，点2横向膨胀速度极值随填充物密度的变化是非单调的，当填充物密度为5 g/cm3时，横向膨胀速度极值最大，即该密度填充物情况下，填充物传递给扁平管的横向瞬时冲量最大。点2横向膨胀位移极值随填充物密度增大而减小。对比曲线5，2，6，7，随着填充物弹性模量的变化，曲线的变化趋势近似，其中，填充物弹性模量为1 GPa时，点2达到速度极值时间最短。随着填充物弹性模量的增加，点2速度极值和位移极值都增加，与点1所得到的结论相反。分析原因，扁平管组件的长轴明显长于短轴，增大填充物的弹性模量，纵向的刚度增加的更多，炸药在爆炸作用过程中会更加倾向于使扁平管向横向发展，并且，在变形的过程中会将填充物向上下两侧挤压， 进一步减小横向的刚度增加纵向的刚度，因此，扁平管点2的横向膨胀速度和位移随着填充物弹性模量的增加而增大。扁平管在实际使用中，其横向的大变形为有效部分，而纵向的膨胀变形对结构的分离不会起作用并且会向结构上部传播冲击，因此，增大填充物的弹性模量很有工程意义。

(a) 横向速度-时间曲线

(b) 横向位移-时间曲线

Fig.12 Simulation velocity results at point 2 of expanding tube with different density and Young’s modulus of the filler material

表9填充物密度及弹性模量不同时扁平管点2膨胀速度及位移极值

Tab.9Extremetransverseexpandingvelocityanddisplacementatpoint2ofexpandingtubewithdifferentdensityandYoung’smodulusofthefillermaterial

编号1234ρ(g·cm-3)0.50.9559vxmax/(m·s-1)236.35238.49252.66233.70dxmax/mm9.189.098.578.28编号5267E/GPa13713vxmax/(m·s-1)221.73238.49266.74279.16dxmax/mm8.779.099.389.56

输出扁平管的动能变化曲线，如图13所示，扁平管的动能极值如表10所示。比较1，2，3，4曲线，随着填充物密度的增加，扁平管获得的动能减小，由于填充物密度增加时，其质量增加，从爆炸产生的能量中分配到的能量增加，扁平管分配到的动能减小。比较5，2，6，7曲线，随着填充物弹性模量的增加，扁平管获得的动能增加，由于填充物弹性模量增加，其变形难度增加，因其变形而消耗的能量减小，炸药的能量更多的传递给扁平管。

图13 填充物密度及弹性模量不同时扁平管动能仿真结果

Fig.13 Simulation kinetic energy results of expanding tube with different density and Young’s modulus of the filler material

表10填充物密度及弹性模量不同时扁平管的动能极值

Tab.10ExtremekineticenergyresultsofexpandingtubewithdifferentdensityandYoung’smodulusofthefillermaterial

编号1234ρ/(g·cm-3)0.50.9559Ek/J802.13738.61483.33388.63编号5267E/GPa13713Ek/J640.86738.61799.05820.20

4 结 论

本文对不同自由扁平管组件在爆炸载荷作用下的膨胀速度、膨胀位移及动能进行了研究。其中，对壁厚为0.8 mm的扁平管进行了实验研究，实验结果和仿真结果吻合较好。在有限元仿真中分别改变扁平管的壁厚，填充物的密度、弹性模量，得到了扁平管横向和纵向膨胀速度、膨胀位移以及扁平管动能的变化规律。主要得出以下结论：

(1) 自由扁平管在炸药爆炸作用下横向膨胀速度和膨胀位移都大于纵向。其在横向先膨胀后收缩，纵向先膨胀后收缩再膨胀。

(2) 在一定范围内，随着扁平管壁厚的增加，其膨胀速度和膨胀位移都减小。扁平管所获动能随壁厚非单调变化，扁平管壁厚为1.2 mm时，其获得的动能最大。

(3) 对于填充物密度不同的扁平管组件，在一定范围内，随着填充物密度的增加，其纵向膨胀速度、纵向膨胀位移、横向膨胀位移以及扁平管动能的极值减小。当填充物密度为5 g/cm3时，扁平管横向膨胀速度极值最大。

(4) 在一定范围内，随着填充物弹性模量的增加，扁平管纵向的膨胀速度和膨胀位移极值减小，扁平管横向的膨胀速度和膨胀位移极值增加，扁平管的动能极值增加。