矩阵方程AXAH=B的Hermitian R-对称形式的最小二乘解

张秀英

(长春师范大学国际教师教育学院，吉林长春 130032)

在科学计算及工程应用等很多领域都需要求解线性矩阵方程. 特别地，许多学者研究了矩阵方程

AXAH=B.

(1)

的特殊形式的解，其中A∈Cm×n,B∈Cm×m[1-6].Khatri[1]给出了方程(1)的Hermitian解的表达式，Tian[2]给出了其最小二乘解和最小秩解的关系，Wei[3]和Zhang[4]研究了此方程在秩约束条件下的Hermitian非负定解.

设R∈Cn×n是一个非平凡的酉对合矩阵，即R=RH=R-1≠I，如果X∈Cn×n满足RXR=X，则称矩阵X是R-对称的[7].令Φ为n阶Hermitian R-对称矩阵的集合，即Φ={X∈Hn×n|RXR=X}，本文研究如下最小二乘问题：

(2)

其中，A,B为系数矩阵，A∈Cm×n，B∈Cm×m.进一步地，寻找该最小二乘问题的极小范数最小二乘解.

文中，Un×n，Hn×n分别表示n×n阶的酉矩阵和Hermitian矩阵的全体，AH是矩阵A的共轭转置，分块矩阵中的单位块和零块分别用I，O来表示.A⊗B、A*B分别为矩阵A与B的Kronecker积与Hadamard积，‖·‖表示取Frobenius范数.

1 Hermitian R-对称矩阵的结构

令r,s分别表示酉对合矩阵R的两个特征值1和-1的特征子空间的维数，则r,s≥1并且r+s=n.令

P=(p1,p2,,pr)，Q=(q1,q2,,qs).

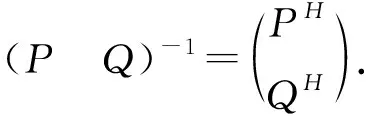
因此，R有以下分解形式：

(3)

对于任意的X∈Hn×n，相应地有如下分块形式：

(4)

其中，X1=PHXP∈Hr×r,X2=QHXQ∈Hs×s,Y=PHXQ∈Cr×s.由式(3)和(4)可得：

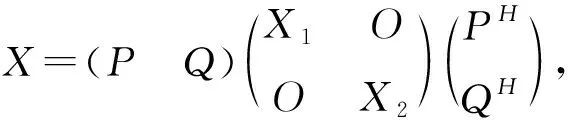
为讨论方便，引入以下记号和分块形式：

A1=AP∈Cm×r,A2=AQ∈Cm×s.

(5)

对A1,A2进行约化的奇异值分解.

(6)

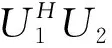
(7)

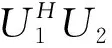
(8)

其中，对角矩阵D的元素小于1.相应地，根据D12的分块形式对U12,V12进行分块.

(9)

2 Hermitian R-对称形式的最小二乘解

对于最小二乘问题(2)，由引理1，

因此，

(10)

最小二乘问题(2)可以转化为求解下面方程的Hermitian最小二乘解：

(11)

引理2 对于矩阵方程：

(12)

其中，A,B,C,D,E已知，X,Y是解矩阵，它的正规方程是：

证明 方程(12)等价于下面的线性系统：

此线性系统的正规方程是：

将等号左边的两个系数矩阵相乘，再次利用Kronecker积，得到矩阵方程(12)的正规方程.

引理3[1]线性矩阵方程(1)有Hermitian解当且仅当AA+B=B,B=BH.这时，其Hermitian解可以写成下面的形式：

X=A+B(A+)H+(In-A+A)V+VH(In-A+A).

其中，V∈Cn×n任意. 更进一步，‖X‖2=‖A+B(A+)H‖2+‖(In-A+A)V+VH(In-A+A)‖2.

(13)

将式(9)代入(13)，可得：

(14)

(15)

显然式(15)中的对角块是Hermitian矩阵. 令

(16)

基于以上矩阵的分块表示(14)～(16)，可以得到下面的结论.

(17)

其中，

C是Hermitian阵，T1,T2是满足维数要求的任意复矩阵.

证明 当X∈Φ，由式(10)(11)和引理2可知，求方程(1)的Hermitian R-对称形式的最小二乘解等价于解下面的正规方程：

(18)

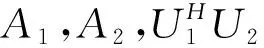
(19)

代入式(13)，方程(19)等价于求解下面方程的Hermitian解：

(20)

将式(14)(15)的分块形式代入式(20)，

(21)

方程组(21)中等号左边的块矩阵除了Ψ11和Φ11都是确定的.

式(14)中的对角块是Hermitian矩阵，Ψ11+Φ11=∑11=Ω11.设Ψ11=C,则Φ11=∑11-C.因此，

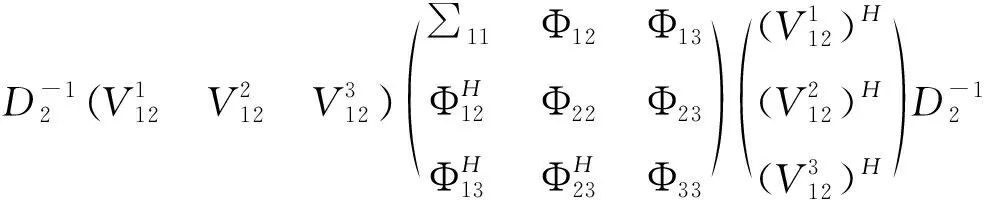
由引理3，得到方程(1)的Hermitian R-对称最小二乘解的表达式.

3 极小范数解

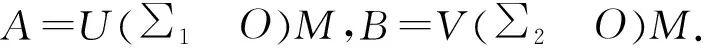
(22)

(23)

U=(U1,U2,U3),V=(V1,V2,V3),

(24)

(25)

记

(26)

基于以上矩阵的分块表示(24)～(26)，下面的结论成立.