基于改进型单周控制的MMC系统三相不平衡控制法

2018-12-20赵剑锋缪惠宇

现代电力 2018年6期

丁然，梅军，赵剑锋，缪惠宇，王创，管州，田杰

(1.东南大学电气工程学院，江苏南京 210096；2.南京南瑞继保电气有限公司，江苏南京 211102)

0 引言

随着电力系统的飞速发展，国内外对电网稳定性与可靠性的提高以及发展可再生清洁能源的要求越来越重视。为此，能够改善电网电能质量、提高供电容量、隔离故障区域，同时方便可再生能源及储能装置灵活接入的柔性直流技术就成为了智能电网领域的研究热点[1]。在组成柔性直流电网的各类设备中，变流器是关键的支撑设备。德国学者R. Marquart在2003年提出的一种新型模块化多电平变流器(modular multilevel converter，MMC)拓扑[2]因具有可扩展模块化结构、众多的电平输出及低谐波输出、有功无功独立控制、以及避免多开关器件串联的动态均压问题等优势，现已在高压直流输电(high voltage direct current，HVDC)、电力传动、电能质量问题治理等领域得到广泛应用[3-4]。

关于MMC的三相不平衡控制研究近年来已经成为本领域关注的热点。由于电网在运行过程中，有可能发生三相电压不平衡，此时系统三相电压和三相电流中存在负序分量，MMC系统内部会产生零序环流流入直流侧，使得直流侧电压产生二倍频谐波，影响系统正常运行。因此为提高MMC系统在电力系统中的稳定性和可靠性，需要MMC系统具有在三相不平衡情况下抑制直流侧电压谐波的能力。迄今为止，国内外学者已对不平衡条件下的MMC系统控制进行了一定研究。文献[5]提出了具有正负序电流控制器的双电流控制，但双电流环需要的比例积分(proportional-integral, PI)控制器多达4个；文献[6-7]提出了包含特定二阶滤波器的辅助控制方案；文献[8-9]提出了比例谐振(proportional-resonant, PR)控制方案；文献[10]提出了准比例积分控制方案；文献[11]提出了比例降阶谐振控制。

由于文献[5-11]的方案使用PR控制器或多个PI控制器，控制器参数设置较为复杂，调试难度较大，且都需要使用由三相电流的实际值运算得出的正负序分量，整体控制系统运算量较大。而单周控制(one-cycle-control, OCC)由于其控制环节简单的特点，已在传统电压源变换器(voltage source converter, VSC)的三相不平衡控制中得到实现[12-13]，但在MMC领域应用较少。文献[14]提出了一种三相平衡情况下基于载波层叠调制和单周控制的MMC并网逆变策略，一定程度上简化了总体控制，但未针对三相不平衡情况进行讨论。

本文提出一种基于改进型单周控制的MMC系统三相不平衡控制策略，通过网侧负序电压补偿MMC网侧电流反馈量，成功削弱直流侧电压的二倍频谐波，实现三相不平衡条件下MMC的单周控制。该策略仅需要使用一个PI控制器，不需要将三相电流的实际值转化为正负序分量，从而避免了文献[5-11]中需要使用多个控制器所引起的参数调节困难，减少了运算过程的复杂度。本文还将虚拟循环映射法嵌入总体控制中，实现了子模块均压。

1 MMC的数学模型

图1是MMC三相并网系统拓扑电路图，MMC每相由上下两个桥臂组成，每个桥臂包含N个子模块，另外串联一个桥臂限流电感Larm。Lg为网侧电感，ej为三相电网电压，ujp、ujn、ijp、ijn、ij分别为各相上桥臂电压、下桥臂电压、上桥臂电流、下桥臂电流和输出相电流(j=a, b, c)。

子模块拓扑有多种结构，现投入实际商业运行的工程中一般采用图1中所示的半桥子模块，通过一定的调制策略控制IGBT器件S1、S2产生开通或关断，使子模块在如下两种状态正常工作：S1开通，S2关断，子模块输出电压为子模块电容电压，称为投入状态；S1关断，S2开通，子模块输出电压为0，称为切除状态。MMC正常运行时任意时刻每相有且仅有N个子模块投入。通过特定的调制和控制，使子模块在不同状态转换，就可使得MMC输出多电平波形电压。

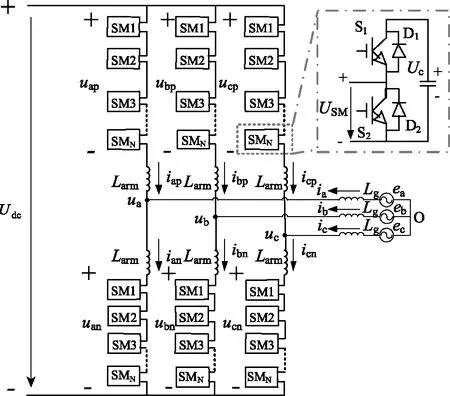
图1 三相MMC系统拓扑Fig.1 Topology of three-phase MMC system

由于MMC正常运行时子模块电容电压须保持动态均衡，因此可忽略子模块电容电压的小范围波动，近似认为其电压恒定，设其平均值为UC。

MMC单相等效电路如图2所示[15]，R为桥臂等效电阻。根据KVL，有

(1)

(2)

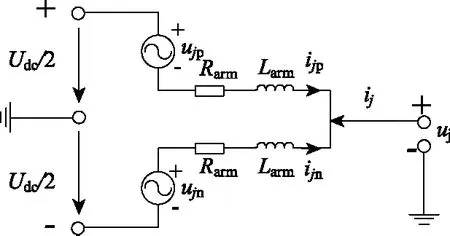
图2 MMC单相等效电路Fig.2 Single-phase equivalent circuit of MMC

在式(1)、(2)中消去Udc，再由KCL可得

(3)

2 三相平衡情况下基本单周控制

由于MMC属于VSC的一种，若把MMC的每个桥臂看成一个整体，则可将文献[17]提出的单周控制下三相PWM整流器的平均等效模型应用在MMC系统中，如图3所示。djL为MMC第j相下桥臂的等效占空比。

因为Lg和Larm的值较小，电感两端基频电压可忽略，所以网侧电压与桥臂占空比有如下关系[18]：

(4)

方程(4)的解不唯一，可解得

(5)

式中k为常数，其值为任意值。由于占空比受到约束条件djL∈(0,1)限制，因此由式(5)可得

(6)

式中Ejm为网侧电压峰值。

MMC运行在单位功率因数情况下时，引入功率等效电阻re和等效电流采样电阻rs[19]，则网侧电压与电流有如下关系：

(7)

式(5)代入(7)，得到如式(8)所示的MMC系统单周控制数学模型：

(8)

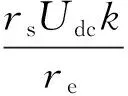
3 三相不平衡时的改进型单周控制

3.1 单周控制在三相不平衡时的负序补偿控制

文献[5-11]虽然都能实现MMC在三相不平衡情况下的控制，但这些文献提出的控制方法均较为复杂，需要使用多个控制器，参数整定较为不易。为了简化控制环节，有必要减少控制器的数量。文献[12-13]提出了针对三相PWM整流器在三相不平衡时的负序补偿控制，由于MMC是VSC的一种，因此可将负序补偿控制加以改造，并应用在MMC系统中。

三相MMC系统连接方式为三相三线制，相电流中不存在零序电流分量，故相电流ij可表示为正负序分量ij+和ij-之和：

ij=ij++ij-,j=a,b,c

(9)

设三相不平衡时网侧相电压滤除零序电压后的值为ejx，网侧相电压正负序分量为ej+、ej-，则有

(10)

三相电网电压出现不平衡时，变流器直流侧电压会出现二次谐波，为抑制此谐波，变流器的有功功率必须为恒定值，设正负序电压相角分别为φe+(t)、φe-(t)，正负序电流相角分别为φi+(t)、φi-(t)即有[12]

(11)

当MMC处于单位功率因数运行时，设MMC的等效正、负序阻抗分别为re+和re-，又有

φe+(t)=φi+(t)

(12)

(13)

联立式(11)、(12)，可得

φe-(t)-φi-(t)=π

(14)

联立式(11)、(13)，并令re=re+，可得

re+=-re-=re

(15)

将式(9)、(13)、(15)代入式(10)，可得

ejx=reij+2ej-,j=a,b,c

(16)

且由于网侧零序电压对MMC正常运行不产生影响，因此可将式(5)改写为

(17)

式中djL为三相不平衡时MMC第j相下桥臂的等效占空比。将式(17)代入(16)，可得电网不平衡时MMC系统单周控制数学模型：

(18)

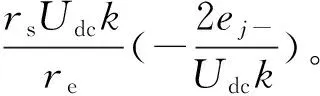
(19)

根据式(19)，MMC系统在三相不平衡情况下仅需使用一个PI控制器实现控制，这样就减少了需要整定的参数数量，降低了控制难度。

3.2 系统总体控制

MMC系统存在固有的子模块电容均压问题。传统单周控制分配给各子模块的脉冲会使得各子模块充放电不均匀，因此各子模块电容电压会发生动态偏移，使MMC输出电压产生畸变，影响MMC的正常工作。传统的均压控制往往使用子模块电容电压排序实现[20]，计算量较大。因此为实现子模块电容均压，本文将一种虚拟子模块循环映射法嵌入单周控制的总体控制中，无需进行子模块电容电压排序，控制简单。

文献[21]介绍了虚拟子模块循环映射法。该方法引入了“虚拟子模块”的概念，将调制策略输出的脉冲信号依次分配给虚拟子模块，再通过构造虚拟子模块与实际子模块之间的映射关系，使得各实际子模块投入和切除概率相同，从而实现各实际子模块均匀充放电，这样就达到了子模块电容均压的目的。

为简化分析过程，本文以MMC每个桥臂子模块数量为4的情况进行说明。

表1给出了MMC第j相的虚拟子模块脉冲的真值，表中将MMC单相输入相电压Uj的范围划分为4个区域。VSM1～VSM4代表上桥臂的4个虚拟子模块，VSM5～VSM8代表下桥臂的4个虚拟子模块。状态“1”表示该虚拟子模块投入，状态“0”表示该虚拟子模块切除，状态“PWM”表示该虚拟子模块的投入或切除由与子模块等效占空比对应的PWM信号决定，每区域内上下桥臂各仅有一个虚拟子模块处于PWM状态。

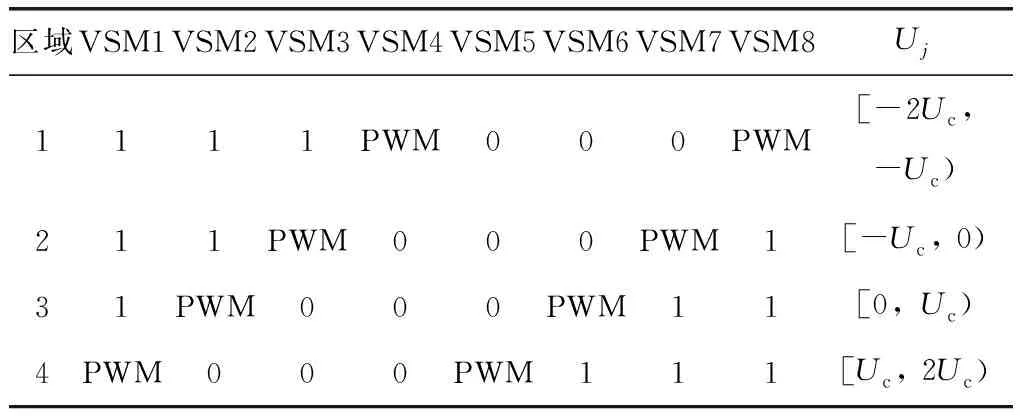
表1 虚拟子模块脉冲真值

设下桥臂VSM5～VSM8中唯一处于PWM状态的虚拟子模块等效占空比为DjL(j=a, b, c)，为保持每相有且仅有N个子模块投入，同一区域内上桥臂VSM1～VSM4的唯一处于PWM状态的虚拟子模块等效占空比为(1-DjL)。根据伏秒平衡原理，当MMC工作在各个区域时，可推导DjL与djL之间关系如下：

区域1：

(20)

区域2：

(21)

区域3：

(22)

区域4：

(23)

区域1：

(24)

区域2：

(25)

区域3：

(26)

区域4：

(27)

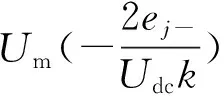
图4给出了虚拟子模块与实际子模块之间的循环映射关系，为了避免开关频率过高，图中的循环映射顺序采取了如文献[22]所示的最佳循环映射顺序，最大限度降低了开关频率。

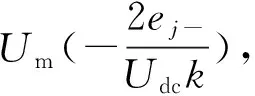
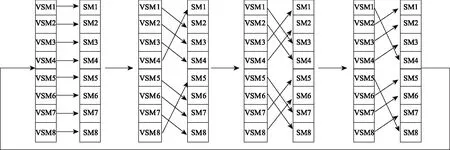
图4 最佳循环映射顺序Fig.4 Prior sequence of loop mapping

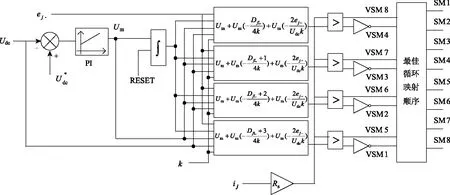
图5 总体控制Fig.5 Overall control

由于总体控制只需计算三相电压正负序分量，不再需要三相电流的正负序分量，因此实时计算量大为降低。

4 仿真结果

为验证本文提出的改进型单周控制法对三相不平衡状态下MMC系统控制的有效性，搭建了基于MATLAB/Simulink软件平台的三相MMC整流系统仿真模型，仿真参数如表2。

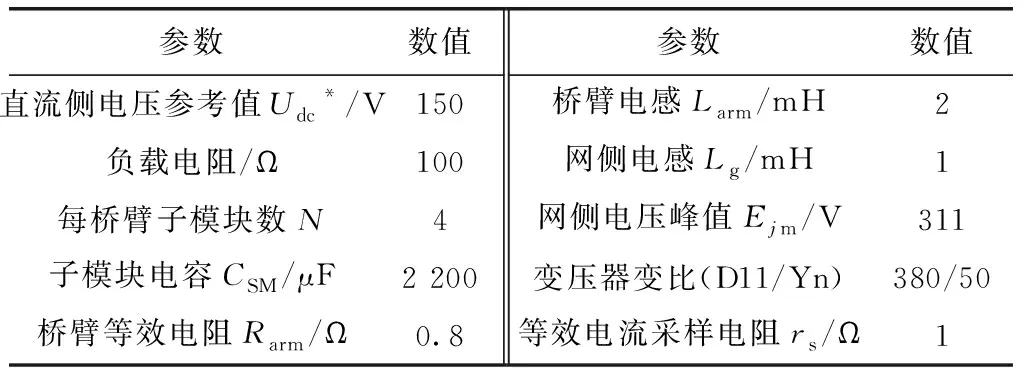
表2 仿真参数

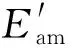
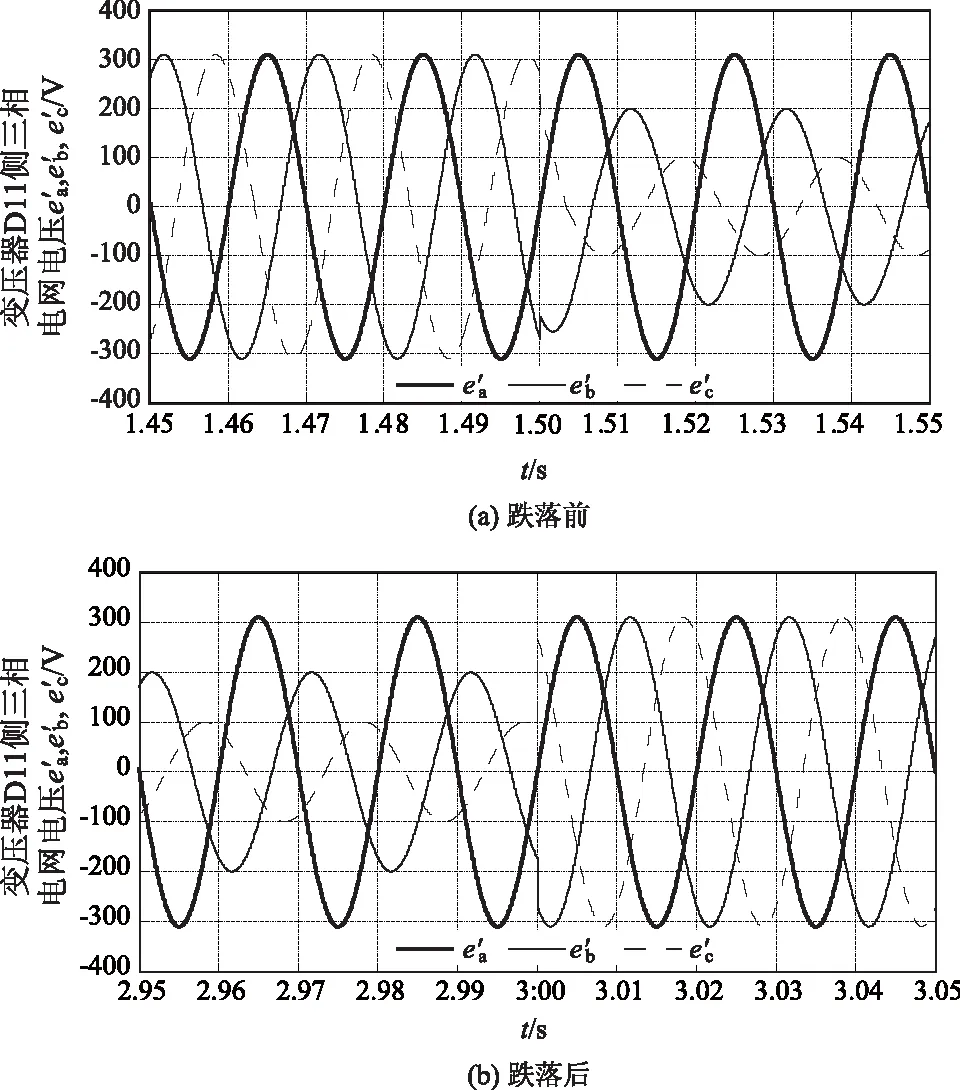
图6 电网电压跌落前后波形Fig.6 Waveforms before and after grid voltages dip

图7展示了在基本单周控制下MMC系统的响应波形。图7(a)说明直流侧电压Udc在三相不平衡发生后产生了二倍于工频的谐波，其谐波信号峰峰值约为2.51V。

图7 基本单周控制下仿真波形Fig.7 Simulation waveforms with basic one-cycle-control

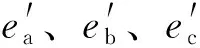
图8显示了使用本文所提出的改进型单周控制法所得到的仿真波形。在1.5s时刻之前，直流侧电压Udc已经稳定在参考值150V，此时系统处于正常运行状态；当1.5s时刻发生三相不平衡以后，如图8(a)所示，直流侧电压Udc在电压跌落后产生的二倍频谐波相比图7(a)大为减小，峰峰值仅为0.60V，相比基本单周控制时降低了76.1%；当3.0s时刻电网电压恢复三相平衡以后，直流侧电压Udc能够回复到参考值150V，说明系统恢复到了正常运行状态。

图8 改进单周控制下仿真波形
Fig.8 Simulation waveforms with improved one-cycle-control

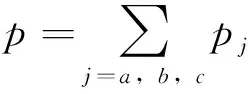
比较图8(d)、(e)可知，A相上桥臂的4个虚拟子模块分配到的PWM脉冲信号不均匀，经图4给出的最佳顺序进行循环映射后，A相上桥臂的实际子模块分配到的信号基本均匀。其余桥臂上的子模块同理也得到了较均匀的脉冲信号，这样就减少了总体器件损耗，延长了器件使用寿命。并且由于各子模块充放电较均匀，也实现了子模块电容电压均衡，这从图8(f)可以看出，A相桥臂的8个子模块电压稳定在平均值Uc=Udc/N=37.5V附近，保证了MMC系统的正常运行。

综上所述，仿真结果证明了本文提出的改进单周控制法不仅可以实现MMC系统在三相不平衡情况下运行时的直流电压谐波抑制，同时可以减少子模块器件损耗，完成子模块电容均压。