减小逆变器下垂控制中虚拟阻抗所致电压偏差的方法研究
2018-12-20陆善婷杨敏红程军照
陆善婷, 杨敏红, 程军照
(1.上海工程技术大学工程实训中心,上海 201620;2.国网上海市电力公司市南供电公司,上海 201100;3.云南电网有限责任公司电网规划研究中心,云南昆明 650011)
0 引 言
下垂控制是微网中常用的控制方法,它包括适用于感性线路的P-f,Q-U下垂[1]和适用于阻性线路的P-U,Q-f下垂[2]。在下垂控制的基础上出现了一些改进方法,其中文献[3]利用线路R/X信息构建虚拟有功和虚拟无功,组成新的下垂控制,文献[4]对此也有介绍,该方法适用于各种线路阻抗特性,但有时R/X信息难以获取;基于虚拟阻抗的下垂控制能灵活改变线路阻抗,具有很强的适应性[5-6]。此外,还有改善动态性能的自适应下垂控制方法[7]。
下垂控制会导致频率偏差,针对该问题有学者提出了P-δ、Q-U下垂控制[8],可以消除频率偏差。下垂控制的另一个主要问题是会带来电压偏差,引入虚拟阻抗会使电压偏差更加突出。为了解决这一问题,文献[9]提出了一种电压恢复机制,但该方法需要所有DG精确地在同一时刻进行电压调整,对时间同步要求极高。文献[10]提出了定期修改下垂系数的控制方法,可以减小下垂引起的频率和电压偏差,但无法消除虚拟阻抗引起的电压偏差,且需要所有DG精确地在同一时刻调整下垂系数,对时间同步系统要求极高。文献[11]提出了容性虚拟阻抗的方法,改善微网电压,但该文未定量分析容性虚拟阻抗对电压的影响以及如何选择容性虚拟阻抗的大小。文献[12]提出了一种控制方法,可以提高微网电压质量且不需要严格的时间同步,但该方法需要DG和其相邻DG之间存在通信。文献[13]提出了一种控制方法,可以提高微网电压质量,但该文仅适用于等容量DG的控制,无法实现不等容量逆变器的负荷按比例分担。文献[14]提出了基于功率坐标变换相结合的方法,可以大幅减小频率偏差,但无法消除虚拟阻抗所致的电压偏差。
本文针对虚拟阻抗带来的电压偏差问题,提出了一种新的控制方法。该方法以下垂控制,虚拟阻抗以及功率坐标变换相结合的方法为基础,根据微网总负荷的功率因数,通过虚拟阻抗合理选择,消除虚拟阻抗造成的电压偏差纵分量,从而大幅减小了电压偏差。本文方法不需要通信,不仅可实现不等容逆变器并联运行时的负荷按比例分担,而且可大幅减小虚拟阻抗所致的电压偏差,仿真结果表明了本文所提方法的有效性。
1 虚拟阻抗的原理
并联逆变器可等效为电压源与系统阻抗串联的形式,如图1所示。图中:E和φ分别为电压和功角;Z和θ分别为线路阻抗的模和阻抗角;R和X分别为线路电阻和感抗;Ub为交流母线电压有效值。
(1)
(2)
逆变器注入微网的有功及无功如式(1)和式(2)所示。当线路为感性,由式(1)、(2)可知,P主要取决于相角差,Q主要取决于电压幅值差,此时可使用P-f、Q-U下垂;当线路为阻性时,由式(1)、(2)可知,P主要取决于电压幅值差,Q主要取决于电压相角差,此时可使用P-U、Q-f下垂。但微网线路的电阻和电感具有可比性,有功P和无功Q之间存在较强的耦合,下垂控制的性能受到较大影响。
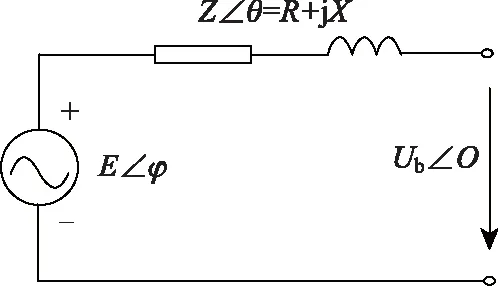
图1 并联逆变器等效电路图Fig.1 Equivalent circuit model for parallel inverter
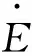
(3)
由式(3)可知,由于虚拟阻抗Zv是人为设置的量,可以按照要求配置,从而灵活地改变线路等效阻抗。
2 功率坐标变换控制方法
假设Zv=Rv+jXv为加入的虚拟阻抗,则可以得到:
(4)
(5)
利用参考文献[3]中的方法,进行功率坐标变换得到:
(6)
(7)
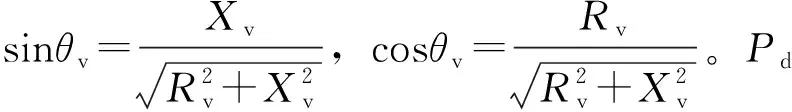
(8)
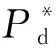
下面需要研究如何实现P和Q的按比例分担。
由(6)、式(7)可得(9)、(10):
P=Pdsinθv+Qdcosθv
(9)
Q=Qdsinθv-Pdcosθv
(10)
根据(9)、(10),任意两个编号为i、j且额定容量为Si、Sj的DG的P、Q之比如式(11)和(12)所示:
(11)
(12)
仔细观察(11)、(12)式可知,若广义功率满足式(13):
(13)
根据等比定理可得式(14):
(14)
通过式(13)和式(14)可知,要实现逆变器P和Q的按容量比例分担,只需控制逆变器的Pd和Qd按逆变器的容量比例分配即可。由文献[14]可知,为实现这一目标,只需按照逆变器额定容量的反比选择广义有功下垂系数m和虚拟阻抗Zv=Rv+jXv。
3 电压偏差的减小
虚拟阻抗会导致电压偏差,且虚拟阻抗值越大,电压偏差也越大,分析如下:
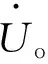
(15)
(16)
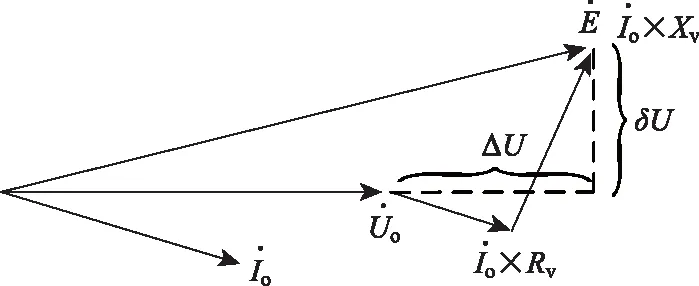
图2 虚拟阻抗导致的电压偏差Fig.2 Voltage deviation due to virtual impedance
由图2所示,电压偏差主要取决于纵分量ΔU,由式(15)可知,纵分量ΔU的大小和虚拟阻抗有关,由于虚拟阻抗是任取的,如果虚拟阻抗满足式(17),就可使电压偏差的纵分量ΔU为零。
式中:S为该逆变器的额定容量;SΣ为微网中所有DG额定容量之和;PΣ、QΣ分别为微网总有功及总无功之和;δ为微网总负荷的功率因数角,由于微网负荷功率因数并非确定值,给应用带来一定困难。假设按照功率因数角δ0取虚拟阻抗,将δ0代入式(17)得式(18):
PRv+QXv=(Scosδ0)Rv+(Ssinδ0)Xv=0
(18)
由于实际负荷功率因数角是变动的,并非总是保持在δ0,下面对负荷功率因数变化时上述处理方法所造成的误差进行分析,假设负荷功率因数角在δ0的基础上变化了Δδ,代入式(15)得式(19):
(19)
结合式(18)对式(19)进行化简得到式(20):
(20)
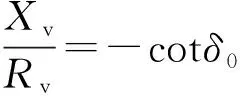
(21)
式中:λ2为区间上限;λ1为区间下限。
综上所述,本文控制方法的流程为
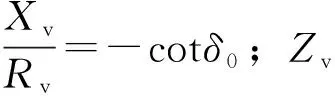
② 用式(8)计算逆变器的频率,积分并乘以2π后得到相角,下垂系数m按照逆变器额定容量的反比选取。
③ 对于每台逆变器,选择相同的电压值E,按照式(22)计算逆变器ABC三相的指令电压uref(a)、uref(b)、uref(c):
(22)
式中:ω为工频角频率;Cv为Xv对应的虚拟电容;i(a)、i(b)、i(c)为逆变器三相输出电流。
④ 控制逆变器跟踪其指令电压uref(a)、uref(b)、uref(c)。
4 仿 真
利用Matlab搭建线电压为380V的微网仿真模型,该微网含有两个容量比为1∶2的三相三桥臂逆变器,带两个线性负荷,如图3所示,其中线路阻抗:ZL1=ZL2=0.1+j0.1。仿真共分为两大部分:① 本文方法和文献[14]中的传统虚拟阻抗方法的对比;②负荷功率因数波动时本文方法的控制效果。如无特别说明,本文所列阻抗值均为工频值。
4.1 本文方法和传统虚拟阻抗法的对比仿真
该部分仿真的参数设置为:ZLD1=ZLD2=18.84+j9.42。采用本文方法和文献[14]中的传统虚拟阻抗方法进行仿真,两种方法的参数设置如表1所示。根据两种方法的要求,为了使逆变器按容量比例分担负荷,在本文控制方法和传统虚拟阻抗控制方法中,下垂系数按照逆变器容量反比选择,虚拟阻抗也按照逆变器容量反比选择。
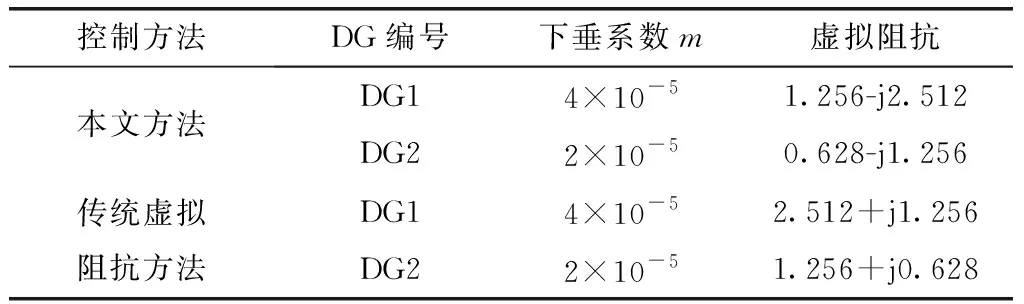
表1 对比仿真参数设置Tab.1 Parameters for comparison simulation
为了更好的对比,两种方法对应的虚拟阻抗的模值是完全相等的,区别在于本文方法对应的参数设置完全符合公式(17)要求,传统虚拟阻抗方法不符合公式(17)要求。
图4是两种方法的负荷分担情况,由此图可以看出:本文方法和传统虚拟阻抗方法都可以基本实现有功P和无功Q的按比例分担。
表2是两种方法输出电压值,其中电压偏差一栏中“/”之前的是本文方法的电压偏差,“/”之后的是传统方法的电压偏差,由此表可知,采用本文方法,虽然引入了较大的虚拟阻抗,但DG输出电压幅值偏差很小,并且负荷增加后,电压偏差增加的幅度也很小;而采用传统虚拟阻抗方法,引入同样模值的虚拟电阻,导致了较大的DG输出电压偏差,而且0.2s负荷增加后,电压偏差也明显增加。

表2 DG输出电压的有效值
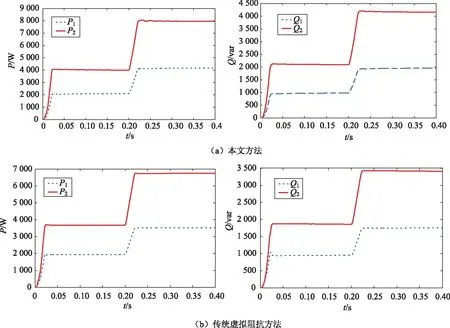
图4 负荷分担情况Fig.4 Power sharing result
4.2 功率因数波动时的仿真
该部分仿真针对负荷功率因数波动时本文方法的效果进行,假设微网负荷波动区间为[0.7,0.9],则根据式(21)计算得到δ0=0.644,Xv/Rv=-1.333,该部分的其他参数设置如表3所示。
DG控制器保持表3所示的参数不变,线性负荷功率因数在[0.7,0.9]之间变动,在负荷功率因数变动过程中,线性负荷ZLD1、ZLD2的模值均保持为21.063 8Ω。对上述情况进行仿真,得到不同负荷功率因数下DG输出电压值,如表4所示。

表3 功率因数波动时仿真参数设置Tab.3 Control parameters for simulation in case of power factor variation
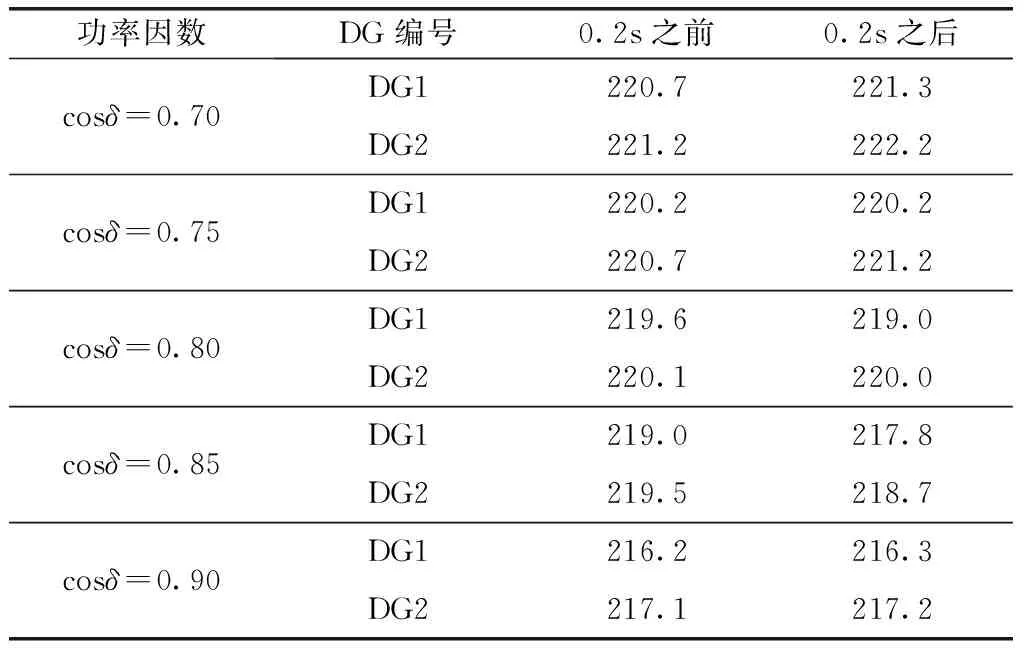
表4 微网负荷功率因数变动时DG输出电压
由表4可知,采用本文方法,负荷功率因数在一定区间内变动时,DG输出电压的偏差仍然很小,相比于额定值220V,电压最大偏差为1.7%,本文方法仍然具有较好效果。
5 结 论
本文对一种减小微网虚拟阻抗控制中电压偏差的方法进行了研究,得出以下结论:
① 虚拟阻抗所致电压偏差包括纵分量和横分量,电压偏差的大小主要由纵分量决定;
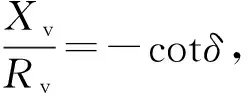
④ 本文方法不需要逆变器之间通信,不仅可实现不等容逆变器并联运行时的负荷按比例分担,而且可大幅减小虚拟阻抗所致的电压偏差,仿真结果表明了本文所提方法的有效性。
