基于二自由度内模控制的LCL并网逆变器控制策略

赵 曦，杨洪耕

(四川大学电气信息学院，四川成都 610065)

0 引 言

近年来，随着煤、石油和天然气等化石能源逐渐枯竭，能源危机越发严重，开发太阳能、风能等可再生能源实现并网发电是解决当前能源危机的必然趋势。由于光伏和风能等新能源的渗透率逐步加大，并网逆变器作为将可再生能源转化为电能的关键设备对电网稳定性和电能质量带来很大的挑战[1]。LCL型滤波器与L型滤波器相比，在等量电感材料下前者具有更好的滤波效果[2]， 但是考虑到LCL型滤波器是一个三阶低阻尼系统，易产生谐振，从而会影响到系统的稳定性，因此需要对系统进行必要的阻尼控制[3]。

目前LCL并网逆变器通常采用两种方式来增加系统阻尼或是来抑制系统谐振[4-8]，即无源阻尼方式和有源阻尼方式。其中无源阻尼方式，是通过串联或并联电阻(滤波器电路中)来抑制LCL滤波器的谐振尖峰，该方法优点是较为容易实现，但此举会增加逆变器损耗，同时也削弱了LCL滤波器对高次谐波的抑制能力；而有源阻尼的方式则是通过在控制回路中引入额外的控制方式(即反馈控制)，从而达到了同样的抑制谐振的效果， 避免了采用无源阻尼方式产生的逆变器损耗。文献[4]和[5]提出对LCL滤波器的电容电流进行采样，再进行反馈控制的方法，此举增加了系统的阻尼。但由于滤波器自身缺陷，其高频电容电流幅值比较小，从而导致了在对采样的数据精确处理时，难度增加，且在硬件方面，也需要增加额外的电流传感器。文献[6]提出采用网侧电感电压微分量来取代滤波器的电容电流的方法，从而抑制谐振尖峰；文献[7]提出通过反馈滤波器中电容电压微分量的方法来实现对谐振阻尼的控制，文献[6-7]中的方法都会导致传感器数量增加。文献[8]则是通过计算当前电容电流的估计值的方法来抑制谐振的产生。虽然此种方法并没有在电路中增加额外的传感器，但是该方法耗时且极为复杂，容易导致误差的产生。

为此，本文将内模控制应用于并网逆变器系统。首先，基于内模控制基本原理，提出一种二自由度内模控制的LCL并网逆变器控制策略，该控制器仅有两个可调参数，其取值与它的控制性能直接相关，再而这种方法可以分别对系统给定信号的跟随性能和抗干扰性能进行调整。然后，仿真对比传统PI控制器和基于二自由度内模控制器的工作特性。最后，搭建不同控制方法下的并网逆变器模型。仿真结果表明, 基于二自由度内模控制器控制器具有良好的跟随性、抗干扰性和鲁棒性, 验证了本文方法的有效性。

1 内模控制基本原理

内模控制(internal model control, IMC)是由Garcia和Morari于1982年在史密斯估计补偿控制这一理论的基础上提出的一种基于过程数学模型进行控制器设计的新型控制策略[9]。由于内模控制具有结构简单、易于在线调整和抗扰性能良好等优点，在实际生产中取得了非常广泛的应用。

典型的内模控制结构图如图1所示，G(s)为被控对象，P(s)为其内部模型，Cimc(s)为内模控制器，R(s)为控制系统的输入，Y(s)为控制系统的输出，D(s)为干扰信号。

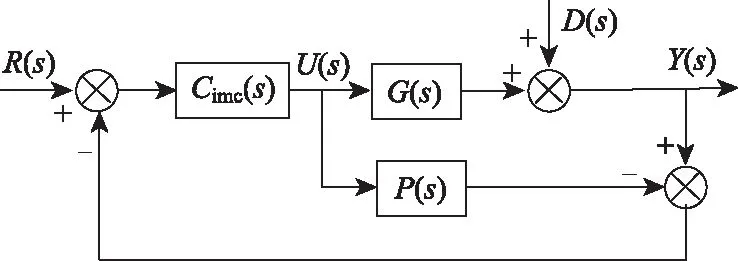
图1 内模控制结构图Fig.1 Block diagram of IMC

对图1进行等价变换为经典反馈控制形式如图2所示。图中，虚线部分为反馈控制器F(s)，由图2可得

(1)

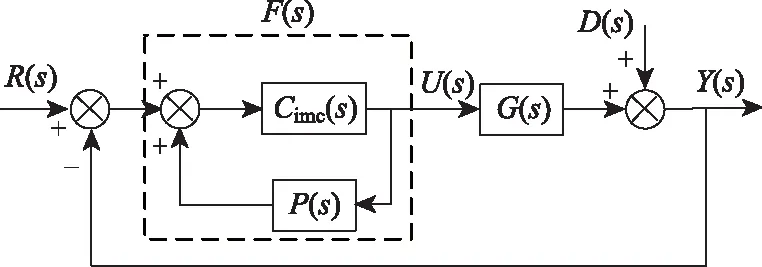
图2 IMC等效反馈控制框图Fig.2 Equivalent feedback control block diagram of IMC

系统闭环响应传递函数可表示为

(2)

对于IMC系统，当模型精确时，只要令Cimc(s)=P-1(s)，系统输出就等于输入，即可获得理想的设定值跟踪，此时为理想控制器。然而由于实际控制对象往往含有右半平面零点，那么P-1(s)中就存在右半平面极点，导致控制器本身就不稳定，且理想控制器对模型误差极其敏感，因此设计内模控制分为以下两步：第一步要设计一个稳定的理想控制器；第二步，要求引入低通滤波器，通过改变其结构和参数来增加系统的稳定性和鲁棒性。内模控制器的形式如下所示：

Gimc(s)=P-1(s)L(s)

(3)

低通滤波器L(s)=1/(1+λs)n，其中，λ为时间常数，阶次n取决于内部模型的最小相位部分的阶次以使控制器可实现。

2 LCL逆变器并网数学模型

单相LCL并网逆变器拓扑结构如图3所示，其构成主要为微电源、Boost升压电路、逆变电路和LCL滤波器4部分。其中，Boost升压电路将微电源侧的电能传送到逆变器输入直流端，逆变器通过LCL滤波后将交流电馈送至电网。图3中，uinv为逆变器侧的输出电压，iL为其输出电流，ug为电网电压，ig为其并网电流，uC为滤波电容电压，逆变器侧电感Ls，网侧电感Lg和滤波电容C1构成LCL滤波器，R1和R2为电感支路上的寄生电阻。

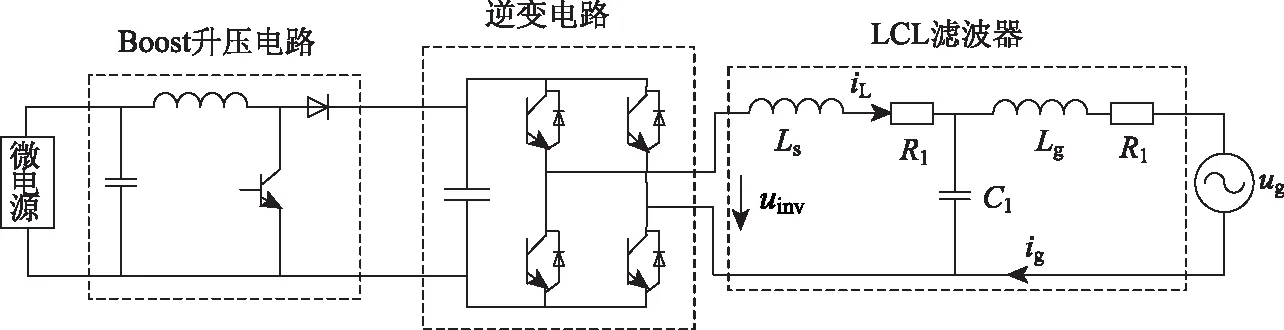
图3 单相LCL并网逆变器拓扑结构Fig.3 The structure of single-phase LCL grid-connected inverter

根据基尔霍夫定律，现选取逆变器侧的电感电流iL、并网电流ig和滤波电容电压uC为状态变量，LCL逆变器的状态空间方程可写为[10]

(4)

由于R1和R2阻值极小，可忽略不计，由式(4)可得到LCL逆变器的模型框图，如图4所示。

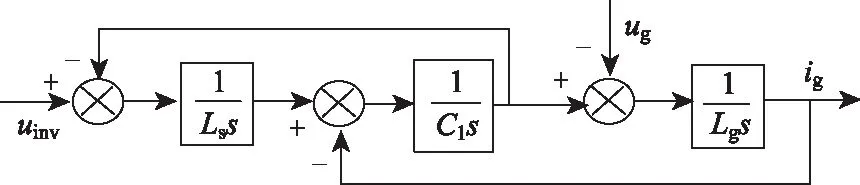
图4 LCL逆变器模型框图Fig.4 Model block diagram of LCL inverter

根据图4，逆变器侧输出电压uinv到并网电流ig的传递函数表达式可表示为

(5)

3 二自由度内模控制并网控制策略

3.1 二自由度内模控制器设计

在常规内模控制器中，一般只有一个可调参数，所以只能选取一个在系统动态性能、鲁棒性这两种性能之间进行折中的办法[11]。本文采用二自由度内模控制，即将主控制器分解为2个独立控制目标值跟随性和抑制扰动的控制器，可在保证系统良好跟踪性能的情况下提高系统的鲁棒性[12-13]，其控制结构如图5所示。

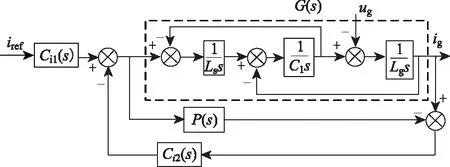
图5 二自由度内模控制结构图Fig.5 Block diagram of 2DOF-IMC

图5中虚线部分为系统被控对象，Ci1(s)和Ci2(s)构成二自由度内模控制器，根据式(3)可得

(6)

其中，低通滤波器L1(s)和L2(s)分别为

(7)

对图5进行等效变换可得到图6。

图6 二自由度内模控制等效反馈控制框图Fig.6 Equivalent feedback control block diagram 2DOF-IMC

其中

(8)

(9)

由图6可知，当只考虑系统跟随性，即ug=0时，可得到

(10)

当只考虑外界扰动，即iref=0时，可得到

(11)

根据式(9)和(10)可知，X(s)只与λ1的大小有关，改变λ1的值可以调整系统对给定信号的跟踪性能，λ1的值越小，系统跟踪性能越好；D(s) 只与λ2的大小有关，改变λ2的值可以调整系统对干扰信号的鲁棒性，λ2的值越小，系统抗干扰性能越好。

3.2 参数设计与稳定性分析

过程模型P(s)可分为P+(s)和P-(s)两项，即

P(s)=P+(s)P-(s)

(12)

式中:P+(s)为模型中的包含纯滞后零点部分和其他不稳定零点部分；P-(s)则为模型中的最小相位部分。

系统的灵敏度函数为

(13)

互补灵敏度函数为

(14)

根据文献[14-15]所提方法，定义最大灵敏度为

Ms=max|S(jω)|

(15)

定义最大互补灵敏度为

MT=max|T(jω)|

(16)

Ms越小，系统抗干扰能力越强，但响应时间变长。给定最大灵敏度初值为Ms0，根据式(15)可得

(17)

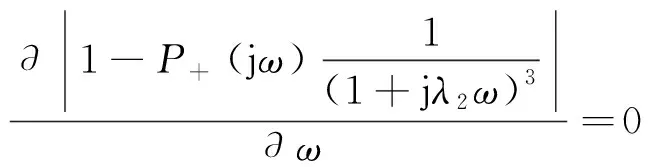
(18)

为了得到较好的跟踪性能，应使MT的值趋近于1。为此，将|T(jω)|取最大值时的频率近似等于|M1(jω)|取最大值时的频率，根据式(16)可得

(19)

(20)

根据式(17)～(20)可求得满足要求的控制器参数λ2和λ1。

则在二自由度内模控制策略下逆变器系统的开环传递函数可表示为

(21)

根据式(5)和(21)可得到逆变器开环传递函数的波特图如图7所示。从图中可以看出，原系统的开环传递函数在2 000Hz附近存在谐振尖峰，而应用本文提出的二自由度内模控制方法明显抑制了谐振尖峰，从而保证了系统的稳定性。

图7 LCL逆变器开环传递函数的波特图Fig.7 Bode plot of open loop transfer function of LCL inventer

4 仿真验证

为验证上述二自由度内模控制器的有效性，在Matlab/Simulink仿真平台上搭建LCL并网逆变器系统仿真模型，逆变器参数如表1所示。二自由度内模控制器的参数为：λ1=0.001，λ1=0.002。对并网逆变器分别采用传统PI控制和二自由度内模控制，进行仿真分析，结果如图8和图9所示。

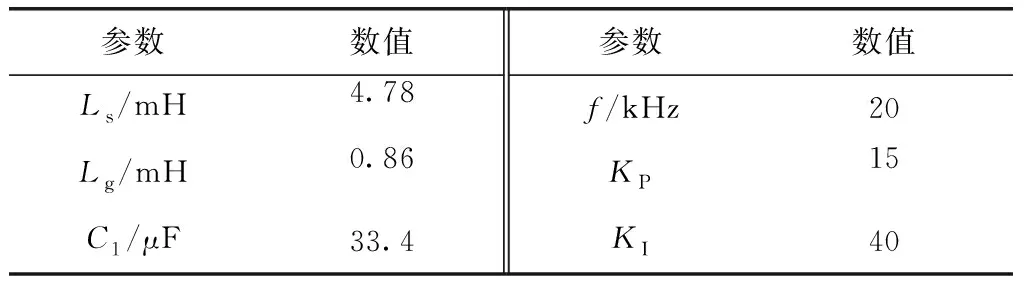
表1 逆变器参数

4.1 电流阶跃响应测试

为了验证系统的跟随性能，将并网电流给定值在0.5s时由半载跃变到满载，图8为并网电流ig的仿真波形,从图中可以看出逆变器并网电流在突变后能稳定运行，且响应速度快、具有良好的动态性能。

图8 并网电流ig波形Fig.8 Waveform of the grid current ig

4.2 并网电流鲁棒性测试

为了验证系统的稳定性，在电网电压中加入12 755rad/s的微量扰动信号。加入微量扰动信号。本文引入的二自由度内模控制方法，与传统PI控制相比，并网电流ig波的波形更加趋于光滑，同时谐振尖峰也得到明显的抑制，其中，采用传统PI控制时，并网电流ig总谐波畸变率达到7.2%，而采用二自由度内模控制并网电流ig总谐波畸变率只有1.4%，远低于国家标准5%，并网电流ig波形如图9所示。

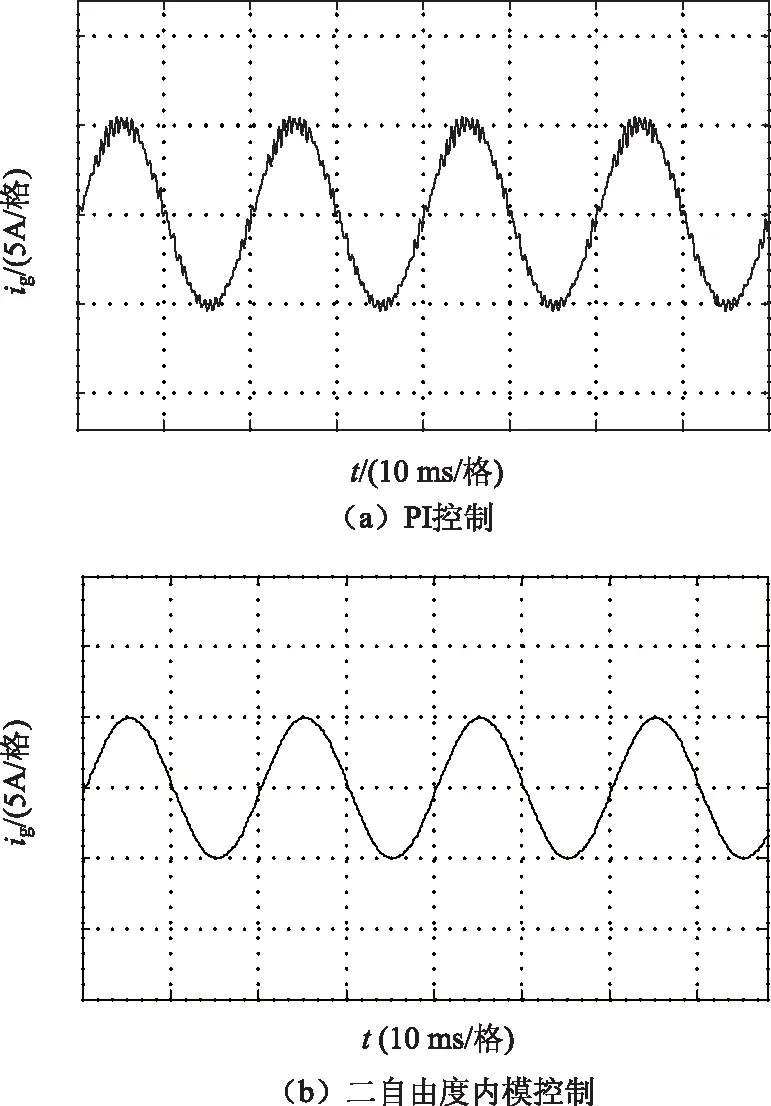
图9 引入扰动时并网电流ig波形Fig.9 Waveform of the grid current ig with the disturbance introduced

5 结 论

① 由于LCL型滤波器是一个三阶低阻尼系统，自身容易出现谐振，需要对其采取一定的控制来增加系统阻尼抑制谐振。现有的LCL并网逆变器有源阻尼控制方法，需要增加额外的传感器，易引起入网电流谐波振荡，从而影响系统运行稳定性。

② 本文提出了一种基于二自由度内模控制的LCL并网逆变器控制策略，该控制器仅有两个可调参数，通过参数整定，所设计的控制器同时具有良好的对给定信号的跟随性能和抑制干扰特性。通过在Matlab/Simulink平台上搭建LCL并网逆变器系统模型，将本文所提出的控制方法与传统PI控制器的控制效果进行了对比，证明了本文所设计的二自由度内模控制器有良好的跟随性和鲁棒性，同时该方法不需要增加额外的电压和电流传感器，具有一定的工程使用价值。